डब्ल्यू अवस्था
डब्ल्यू अवस्था तीन क्वैबिट की क्वांटम उलझाव कितना राज्य है जिसका अच्छा संकेतन में निम्नलिखित आकार होता है
और जो विशिष्ट प्रकार के बहुपक्षीय उलझाव का प्रतिनिधित्व करने और क्वांटम सूचना सिद्धांत में कई अनुप्रयोगों में होने के लिए उल्लेखनीय है। इस अवस्था में तैयार किए गए कण बेल के प्रमेय के गुणों को पुन: उत्पन्न करते हैं, जो बताता है कि स्थानीय छिपे हुए चर का कोई भी शास्त्रीय सिद्धांत क्वांटम यांत्रिकी की भविष्यवाणियां नहीं कर सकता है। राज्य का नाम वोल्फगैंग ड्यूर के नाम पर रखा गया है,[1] जिन्होंने सबसे पहले 2002 में गुइफ़्रे विडाल और जुआन इग्नासियो सिराक सस्टुरैन के साथ मिलकर राज्य की रिपोर्ट की थी।[2]
गुण
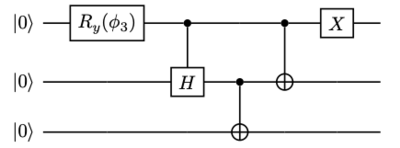
डब्ल्यू राज्य दो गैर-विभाज्य में से का प्रतिनिधि है[3] तीन-क्विबिट राज्यों की कक्षाएं, दूसरा ग्रीनबर्गर-हॉर्न-ज़ीलिंगर राज्य है, , जिन्हें LOCC द्वारा दूसरे में परिवर्तित नहीं किया जा सकता (संभावित रूप से भी नहीं)।[2] इस प्रकार और दो बहुत भिन्न प्रकार के त्रिपक्षीय उलझाव का प्रतिनिधित्व करते हैं।
यह अंतर, उदाहरण के लिए, डब्ल्यू राज्य की निम्नलिखित दिलचस्प संपत्ति द्वारा चित्रित किया गया है: यदि तीन क्विबिट में से खो जाता है, तो शेष 2-क्विबिट प्रणाली की स्थिति अभी भी उलझी हुई है। डब्ल्यू-प्रकार के उलझाव की यह मजबूती जीएचजेड स्थिति के साथ दृढ़ता से विपरीत है, जो क्विबिट के नुकसान के बाद पूरी तरह से अलग हो जाती है।
W वर्ग के राज्यों को मल्टीपार्टाइट उलझाव#शुद्ध राज्यों के लिए मल्टीपार्टाइट उलझाव उपायों के माध्यम से अन्य सभी 3-क्विबिट राज्यों से अलग किया जा सकता है। विशेष रूप से, W राज्यों में किसी भी द्विविभाजन में गैर-शून्य उलझाव होता है,[4] जबकि 3-टेंगल गायब हो जाता है, जो GHZ-प्रकार के राज्यों के लिए भी गैर-शून्य है।[2]
सामान्यीकरण
डब्ल्यू राज्य की धारणा को सामान्यीकृत किया गया है qubits[2]और फिर सभी संभावित शुद्ध अवस्थाओं के समान विस्तार गुणांक वाले क्वांटम सुपरपोजिशन को संदर्भित करता है जिसमें वास्तव में क्वैबिट उत्तेजित अवस्था में होता है , जबकि अन्य सभी जमीनी अवस्था में हैं :
कण हानि के विरुद्ध मजबूती और (सामान्यीकृत) GHZ अवस्था के साथ LOCC-असमानता दोनों भी इसके लिए मान्य हैं -क्विबिट डब्ल्यू अवस्था।
अनुप्रयोग
जिन प्रणालियों में एकल क्वबिट को कई दो-स्तरीय प्रणालियों के समूह में संग्रहीत किया जाता है, तार्किक 1 को अक्सर डब्ल्यू राज्य द्वारा दर्शाया जाता है, जबकि तार्किक 0 को राज्य द्वारा दर्शाया जाता है। . यहां कण हानि के खिलाफ डब्ल्यू राज्य की मजबूती बहुत ही लाभकारी संपत्ति है जो इन संयोजन-आधारित क्वांटम यादों के अच्छे भंडारण गुणों को सुनिश्चित करती है।[5]
यह भी देखें
संदर्भ
- ↑ Cabello, Adán (2002-02-05). "थ्री-क्विट ग्रीनबर्गर-हॉर्न-ज़ीलिंगर और डब्ल्यू राज्यों के लिए असमानताओं के साथ और बिना बेल का प्रमेय". Physical Review A (in English). 65 (3): 032108. arXiv:quant-ph/0107146. Bibcode:2002PhRvA..65c2108C. doi:10.1103/PhysRevA.65.032108. ISSN 1050-2947. S2CID 55659305.
- ↑ 2.0 2.1 2.2 2.3 W. Dür; G. Vidal & J. I. Cirac (2000). "तीन क्वैबिट को दो असमान तरीकों से उलझाया जा सकता है". Phys. Rev. A. 62 (6): 062314. arXiv:quant-ph/0005115. Bibcode:2000PhRvA..62f2314D. doi:10.1103/PhysRevA.62.062314. S2CID 16636159.
- ↑ A pure state of parties is called biseparable, if one can find a partition of the parties in two disjoint subsets and with such that , i.e. is a product state with respect to the partition .
- ↑ A bipartition of the three qubits is any grouping and in which two qubits are considered to belong to the same party. The 3-qubit state can then be considered as a state on and studied with bipartite entanglement measures.
- ↑ M. Fleischhauer & M. D. Lukin (2002). "Quantum memory for photons: Dark-state polaritons". Phys. Rev. A. 65 (2): 022314. arXiv:quant-ph/0106066. Bibcode:2002PhRvA..65b2314F. doi:10.1103/PhysRevA.65.022314. S2CID 54532771.