यादृच्छिक नमूना सर्वसम्मति

रैंडम सैंपल सर्वसम्मति (RANSAC) अवलोकन किए गए डेटा के एक सेट से गणितीय मॉडल के मापदंडों का अनुमान लगाने की एक पुनरावृत्तीय विधि है, जिसमें आउटलेर्स सम्मिलित होते हैं, जब आउटलेर्स को अनुमानों के मानों पर कोई प्रभाव नहीं दिया जाता है। इसलिए, इसकी व्याख्या एक बाहरी पता लगाने की विधि के रूप में भी की जा सकती है। यह इस अर्थ में एक गैर-नियतात्मक एल्गोरिदम है कि यह केवल एक निश्चित संभावना के साथ एक उचित परिणाम उत्पन्न करता है, जैसे-जैसे अधिक पुनरावृत्तियों की अनुमति दी जाती है, यह संभावना बढ़ती जाती है। एल्गोरिथ्म को पहली बार 1981 में एसआरआई इंटरनेशनल में फिशलर और बोल्स द्वारा प्रकाशित किया गया था। उन्होंने स्थान निर्धारण समस्या (LDP) को हल करने के लिए आरएएनएसएसी का उपयोग किया, जहां लक्ष्य समष्टि में उन बिंदुओं को निर्धारित करना है जो एक छवि पर ज्ञात स्थानों के साथ स्थलों के सेट में प्रोजेक्ट करते हैं।

आरएएनएसएसी बार-बार यादृच्छिक उप-नमूनाकरण का उपयोग करता है। एक बुनियादी धारणा यह है कि डेटा में "इनलियर्स" होते हैं, अर्थात, डेटा जिसका वितरण मॉडल मापदंडों के कुछ सेट द्वारा समझाया जा सकता है, हालांकि रव के अधीन हो सकता है, और "आउटलेयर" जो डेटा हैं जो मॉडल में फिट नहीं होते हैं। आउटलेर्स, उदाहरण के लिए, रव के चरम मानों से या गलत माप या डेटा की व्याख्या के बारे में गलत परिकल्पनाओं से आ सकते हैं। आरएएनएसएसी यह भी मानता है कि, इनलियर्स के (सामान्यतः छोटे) सेट को देखते हुए, एक ऐसी प्रक्रिया उपस्थित है जो एक मॉडल के मापदंडों का अनुमान लगा सकती है जो इस डेटा को इष्टतम रूप से समझाती है या फिट करती है।

उदाहरण

एक सरल उदाहरण अवलोकनों के एक सेट में दो आयामों में एक रेखा को फिट करना है। यह मानते हुए कि इस सेट में दोनों इनलियर्स सम्मिलित हैं, अर्थात, बिंदु जो लगभग एक रेखा पर फिट किए जा सकते हैं और आउटलेयर, बिंदु जो इस लाइन पर फिट नहीं किए जा सकते हैं, लाइन फिटिंग के लिए एक सरल न्यूनतम वर्ग विधि सामान्यतः इनलियर्स और आउटलेर्स सहित डेटा के लिए खराब फिट वाली एक लाइन उत्पन्न करेगा। इसका कारण यह है कि यह आउटलेर्स सहित सभी बिंदुओं पर सर्वोत्तम रूप से फिट है। दूसरी ओर, आरएएनएसएसी, आउटलेर्स को बाहर करने और एक रैखिक मॉडल खोजने का प्रयास करता है जो अपनी गणना में केवल इनलियर्स का उपयोग करता है। यह डेटा के कई यादृच्छिक नमूनों में रैखिक मॉडल फिट करके और उस मॉडल को वापस करके किया जाता है जो डेटा के उपसमुच्चय के लिए सबसे उपयुक्त है। चूँकि इनलियर्स इनलियर्स और आउटलेर्स के यादृच्छिक मिश्रण की तुलना में अधिक रैखिक रूप से संबंधित होते हैं, एक यादृच्छिक उपसमुच्चय जिसमें पूरी तरह से इनलियर्स सम्मिलित होते हैं, सबसे अच्छा मॉडल फिट होगा। व्यवहार में, इस बात की कोई गारंटी नहीं है कि इनलियर्स के एक उपसमुच्चय को यादृच्छिक रूप से नमूना किया जाएगा, और एल्गोरिदम के सफल होने की संभावना डेटा में इनलियर्स के अनुपात के साथ-साथ कई एल्गोरिदम मापदंडों की पसंद पर निर्भर करती है।

• 

  कई आउटलेर्स वाला एक डेटा सेट जिसके लिए एक लाइन फिट की जानी है।

• 

  RANSAC के साथ सज्जित लाइन; आउटलेर्स का परिणाम पर कोई प्रभाव नहीं पड़ता है।

अवलोकन

आरएएनएसएसी एल्गोरिथ्म प्रेक्षित डेटा के यादृच्छिक नमूने द्वारा किसी मॉडल के मापदंडों का अनुमान लगाने की एक सीखने की तकनीक है। एक डाटासेट को देखते हुए जिसके डेटा तत्वों में इनलियर्स और आउटलेर दोनों सम्मिलित हैं, आरएएनएसएसी इष्टतम फिटिंग परिणाम खोजने के लिए वोटिंग योजना का उपयोग करता है। डाटासेट में डेटा तत्वों का उपयोग एक या एकाधिक मॉडल के लिए वोट करने के लिए किया जाता है। इस वोटिंग योजना का कार्यान्वयन दो धारणाओं पर आधारित है: रव वाली विशेषताएं किसी एक मॉडल (कुछ आउटलेर्स) के लिए लगातार वोट नहीं करेंगी और एक अच्छे मॉडल (कुछ गायब डेटा) पर सहमत होने के लिए पर्याप्त सुविधाएं हैं। आरएएनएसएसी एल्गोरिथ्म अनिवार्य रूप से दो चरणों से बना है जिन्हें पुनरावृत्त रूप से दोहराया जाता है:

1. पहले चरण में, इनपुट डाटासेट से न्यूनतम डेटा आइटम वाला एक नमूना उपसमूह यादृच्छिक रूप से चुना जाता है। मॉडल मापदंडों के साथ एक फिटिंग मॉडल की गणना केवल इस नमूना उपसमूह के तत्वों का उपयोग करके की जाती है। नमूना उपसमुच्चय की प्रमुखता (उदाहरण के लिए, इस उपसमुच्चय में डेटा की मात्रा) मॉडल मापदंडों को निर्धारित करने के लिए पर्याप्त है।
2. दूसरे चरण में, एल्गोरिदम जांचता है कि संपूर्ण डाटासेट के कौन से तत्व पहले चरण से प्राप्त अनुमानित मॉडल मापदंडों द्वारा तत्काल मॉडल के अनुरूप हैं। एक डेटा तत्व को आउटलेयर के रूप में माना जाएगा यदि यह इनलियर्स के अधिकतम डेटा विचलन को परिभाषित करने वाली कुछ त्रुटि सीमा के भीतर मॉडल में फिट नहीं होता है। (इस विचलन से परे डेटा तत्व आउटलेयर हैं।)

फिटिंग मॉडल के लिए प्राप्त इनलियर्स के समुच्चय को सर्वसम्मति समुच्चय कहा जाता है। आरएएनएसएसी एल्गोरिथ्म उपरोक्त दो चरणों को तब तक दोहराएगा जब तक कि निश्चित पुनरावृत्ति में प्राप्त सर्वसम्मति समुच्चय में पर्याप्त इनलाइनर न हों।

आरएएनएसएसी एल्गोरिथ्म का इनपुट अवलोकन किए गए डेटा मानों का एक समुच्चय है, अवलोकनों के लिए उपयुक्त एक मॉडल और आउटलेर्स को परिभाषित करने वाले कुछ आत्मविश्वास अंतराल मापदंड हैं। उपरोक्त आरएएनएसएसी एल्गोरिथ्म अवलोकन से अधिक विवरण में, आरएएनएसएसी निम्नलिखित चरणों को दोहराकर अपना लक्ष्य प्राप्त करता है:

1. मूल डेटा का एक यादृच्छिक उपसमूह चुनें। इस उपसमुच्चय को काल्पनिक इनलियर्स कहें।
2. एक मॉडल को काल्पनिक इनलियर्स के समुच्चय पर फिट किया गया है।
3. फिर सभी डेटा का परीक्षण फिट किए गए मॉडल के विरुद्ध किया जाता है। सभी डेटा बिंदु (मूल डेटा के) जो कुछ मॉडल-विशिष्ट हानि फ़ंक्शन के अनुसार अनुमानित मॉडल को अच्छी तरह से फिट करते हैं, सर्वसम्मति समुच्चय (अर्थात, मॉडल के लिए इनलियर्स का समुच्चय) कहलाते हैं।
4. यदि पर्याप्त संख्या में डेटा बिंदुओं को आम सहमति समुच्चय के हिस्से के रूप में वर्गीकृत किया गया है तो अनुमानित मॉडल काफी अच्छा है।
5. सर्वसम्मति समुच्चय के सभी सदस्यों का उपयोग करके मॉडल का पुन: आकलन करके इसे बेहतर बनाया जा सकता है। मॉडल सर्वसम्मति समुच्चय पर कितनी अच्छी तरह फिट बैठता है, इसके माप के रूप में फिटिंग गुणवत्ता का उपयोग मॉडल फिटिंग को तेज करने के लिए किया जाएगा क्योंकि पुनरावृत्ति आगे बढ़ती है (उदाहरण के लिए, इस माप को अगले पुनरावृत्ति में फिटिंग गुणवत्ता मानदंड के रूप में समुच्चय करके)।

पर्याप्त रूप से अच्छे मॉडल मापदंड समुच्चय में परिवर्तित होने के लिए, इस प्रक्रिया को निश्चित संख्या में दोहराया जाता है, हर बार या तो मॉडल की अस्वीकृति उत्पन्न होती है क्योंकि बहुत कम बिंदु सर्वसम्मति समुच्चय का हिस्सा होते हैं, या सर्वसम्मति समुच्चय आकार के साथ एक परिष्कृत मॉडल पिछले सर्वसम्मति समुच्चय से बड़ा होता है।

• 

  RANSAC: इनलियर्स और आउटलेर्स। इस उदाहरण में डेटा बिंदुओं की रैखिक फिटिंग 7 इनलियर्स के साथ है (डेटा बिंदु कुछ मानदंडों के तहत मॉडल के साथ अच्छी तरह से फिट होते हैं)। यह एक अच्छी फिटिंग नहीं है क्योंकि इसमें एक रैखिक रेखा होती है जहां अधिकांश डेटा बिंदु इसके पास वितरित होते हैं (यानी, अधिक इनलाइनर्स)।

स्यूडोकोड

सामान्य आरएएनएसएसी एल्गोरिथ्म निम्नलिखित छद्मकोड के रूप में काम करता है:

दिया गया:
    डेटा - अवलोकनों का एक समुच्चय।
    मॉडल - देखे गए डेटा बिंदुओं को समझाने के लिए एक मॉडल।
    n - मॉडल मापदंडों का अनुमान लगाने के लिए आवश्यक डेटा बिंदुओं की न्यूनतम संख्या।
    k - एल्गोरिदम में अनुमत पुनरावृत्तियों की अधिकतम संख्या।
    टी - डेटा बिंदुओं को निर्धारित करने के लिए एक थ्रेशोल्ड मान जो मॉडल (इनलीयर) द्वारा अच्छी तरह से फिट होता है।
    डी - यह सुनिश्चित करने के लिए आवश्यक करीबी डेटा बिंदुओं (इनलियर्स) की संख्या कि मॉडल डेटा के साथ अच्छी तरह से फिट बैठता है।

वापस करना:
    बेस्टफ़िट - मॉडल मापदंड जो डेटा के लिए सबसे उपयुक्त हो सकते हैं (या यदि कोई अच्छा मॉडल नहीं मिलता है तो शून्य)।


पुनरावृत्तियाँ = 0
बेस्टफ़िट = शून्य
bestErr = कुछ वास्तव में बड़ा // इस मापदंड का उपयोग पुनरावृत्तियों के चलते मॉडल मापदंड को सर्वोत्तम डेटा फिटिंग में तेज करने के लिए किया जाता है।

जबकि पुनरावृत्तियां < k करते हैं
    mayInlierss:= n डेटा से बेतरतीब ढंग से चयनित मान
    हो सकता है मॉडल�:= मॉडल मापदंड शायद इनलियर्स में फिट किए गए हों
    कन्फर्मइनलियर्स�:= खाली समुच्चय
    डेटा के प्रत्येक बिंदु के लिए करें
        यदि बिंदु हो सकता है कि मॉडल टी से छोटी त्रुटि के साथ फिट बैठता है
             कन्फ़र्मइनलियर्स में बिंदु जोड़ें
        अगर अंत
    के लिए समाप्त
    यदि कन्फ़र्मइनलियर्स में तत्वों की संख्या > d है तो
        // इसका तात्पर्य यह है कि हमें एक अच्छा मॉडल मिल गया होगा।
        // अब परीक्षण करें कि यह कितना अच्छा है।
        बेहतरमॉडल:= मॉडल मापदंड कन्फर्मइनलियर्स में सभी बिंदुओं पर फिट किए गए हैं
        thisErr := यह मापता है कि मॉडल इन बिंदुओं पर कितनी अच्छी तरह फिट बैठता है
        यदि यह त्रुटि < सर्वोत्तम त्रुटि है तो
            बेस्टफ़िट:=बेहतरमॉडल
            bestErr := thisErr
         end if
    अगर अंत
    वृद्धिशील पुनरावृत्तियाँ
समय समाप्त करें

बेस्टफ़िट लौटाएँ

उदाहरण कोड

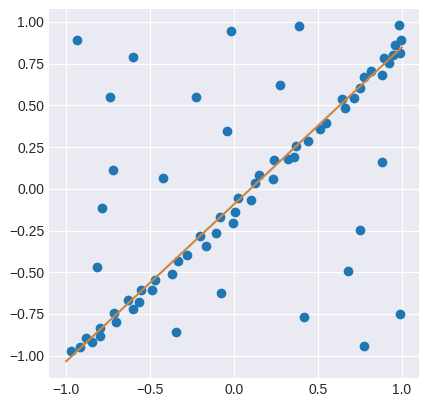
छद्मकोड को प्रतिबिंबित करने वाला एक पायथन कार्यान्वयन है। यह न्यूनतम वर्गों के आधार पर एक LinearRegressor को भी परिभाषित करता है, 2डी प्रतिगमन समस्या पर RANSAC अनुप्रयुक्त करता है, और परिणाम की कल्पना करता है:

from copy import copy
import numpy as np
from numpy.random import default_rng
rng = default_rng()


class RANSAC:
    def __init__(self, n=10, k=100, t=0.05, d=10, model=None, loss=None, metric=None):
        self.n = n              # `n`: Minimum number of data points to estimate parameters
        self.k = k              # `k`: Maximum iterations allowed
        self.t = t              # `t`: Threshold value to determine if points are fit well
        self.d = d              # `d`: Number of close data points required to assert model fits well
        self.model = model      # `model`: class implementing `fit` and `predict`
        self.loss = loss        # `loss`: function of `y_true` and `y_pred` that returns a vector
        self.metric = metric    # `metric`: function of `y_true` and `y_pred` and returns a float
        self.best_fit = None
        self.best_error = np.inf

    def fit(self, X, y):
        for _ in range(self.k):
            ids = rng.permutation(X.shape[0])

            maybe_inliers = ids[: self.n]
            maybe_model = copy(self.model).fit(X[maybe_inliers], y[maybe_inliers])

            thresholded = (
                self.loss(y[ids][self.n :], maybe_model.predict(X[ids][self.n :]))
                < self.t
            )

            inlier_ids = ids[self.n :][np.flatnonzero(thresholded).flatten()]

            if inlier_ids.size > self.d:
                inlier_points = np.hstack([maybe_inliers, inlier_ids])
                better_model = copy(self.model).fit(X[inlier_points], y[inlier_points])

                this_error = self.metric(
                    y[inlier_points], better_model.predict(X[inlier_points])
                )

                if this_error < self.best_error:
                    self.best_error = this_error
                    self.best_fit = maybe_model

        return self

    def predict(self, X):
        return self.best_fit.predict(X)

def square_error_loss(y_true, y_pred):
    return (y_true - y_pred) ** 2


def mean_square_error(y_true, y_pred):
    return np.sum(square_error_loss(y_true, y_pred)) / y_true.shape[0]


class LinearRegressor:
    def __init__(self):
        self.params = None

    def fit(self, X: np.ndarray, y: np.ndarray):
        r, _ = X.shape
        X = np.hstack([np.ones((r, 1)), X])
        self.params = np.linalg.inv(X.T @ X) @ X.T @ y
        return self

    def predict(self, X: np.ndarray):
        r, _ = X.shape
        X = np.hstack([np.ones((r, 1)), X])
        return X @ self.params


if __name__ == "__main__":

    regressor = RANSAC(model=LinearRegressor(), loss=square_error_loss, metric=mean_square_error)

    X = np.array([-0.848,-0.800,-0.704,-0.632,-0.488,-0.472,-0.368,-0.336,-0.280,-0.200,-0.00800,-0.0840,0.0240,0.100,0.124,0.148,0.232,0.236,0.324,0.356,0.368,0.440,0.512,0.548,0.660,0.640,0.712,0.752,0.776,0.880,0.920,0.944,-0.108,-0.168,-0.720,-0.784,-0.224,-0.604,-0.740,-0.0440,0.388,-0.0200,0.752,0.416,-0.0800,-0.348,0.988,0.776,0.680,0.880,-0.816,-0.424,-0.932,0.272,-0.556,-0.568,-0.600,-0.716,-0.796,-0.880,-0.972,-0.916,0.816,0.892,0.956,0.980,0.988,0.992,0.00400]).reshape(-1,1)
    y = np.array([-0.917,-0.833,-0.801,-0.665,-0.605,-0.545,-0.509,-0.433,-0.397,-0.281,-0.205,-0.169,-0.0531,-0.0651,0.0349,0.0829,0.0589,0.175,0.179,0.191,0.259,0.287,0.359,0.395,0.483,0.539,0.543,0.603,0.667,0.679,0.751,0.803,-0.265,-0.341,0.111,-0.113,0.547,0.791,0.551,0.347,0.975,0.943,-0.249,-0.769,-0.625,-0.861,-0.749,-0.945,-0.493,0.163,-0.469,0.0669,0.891,0.623,-0.609,-0.677,-0.721,-0.745,-0.885,-0.897,-0.969,-0.949,0.707,0.783,0.859,0.979,0.811,0.891,-0.137]).reshape(-1,1)

    regressor.fit(X, y)

    import matplotlib.pyplot as plt
    plt.style.use("seaborn-darkgrid")
    fig, ax = plt.subplots(1, 1)
    ax.set_box_aspect(1)

    plt.scatter(X, y)

    line = np.linspace(-1, 1, num=100).reshape(-1, 1)
    plt.plot(line, regressor.predict(line), c="peru")
    plt.show()

मापदंड

यह निर्धारित करने के लिए थ्रेशोल्ड मान कि डेटा बिंदु मॉडल (t) कब फिट बैठता है, और मॉडल डेटा (d) के लिए अच्छी तरह से फिट बैठता है, यह सुनिश्चित करने के लिए आवश्यक इनलियर्स (टी के भीतर मॉडल में फिट किए गए डेटा बिंदु) की संख्या विशिष्ट आवश्यकताओं के आधार पर निर्धारित की जाती है। एप्लिकेशन और डेटासेट का, और संभवतः प्रयोगात्मक मूल्यांकन पर आधारित है। हालाँकि, पुनरावृत्तियों की संख्या (k), मोटे तौर पर सफलता की वांछित संभावना (p) के एक फ़ंक्शन के रूप में निर्धारित की जा सकती है जैसा कि नीचे दिखाया गया है।

मान लीजिए कि p वांछित संभावना है कि आरएएनएसएसी एल्गोरिथ्म चलने के बाद कम से कम एक उपयोगी परिणाम प्रदान करता है। चरम रूप में (व्युत्पत्ति को सरल बनाने के लिए), आरएएनएसएसी एक सफल परिणाम देता है यदि कुछ पुनरावृत्ति में यह इनपुट डेटा सेट से केवल इनलियर्स का चयन करता है जब यह डेटा सेट से n अंक चुनता है जिससे मॉडल पैरामीटर का अनुमान लगाया जाता है। दूसरे शब्दों में, सभी चयनित n डेटा बिंदु इन बिंदुओं द्वारा अनुमानित मॉडल के अंतर्निहित हैं। $w$ प्रत्येक बार एक एकल डेटा बिंदु का चयन करने पर एक अंतर्निहित को चुनने की संभावना होगी, जो मोटे तौर पर है,

$w$ = डेटा में इनलियर्स की संख्या / डेटा में अंकों की संख्या

एक सामान्य स्थिति यह है कि आरएएनएसएसी एल्गोरिदम चलाने से पहले डेटा में अज्ञात संख्या में इनलियर्स के कारण $w$ पहले से अच्छी तरह से ज्ञात नहीं है, लेकिन कुछ मोटा मान दिया जा सकता है। $w$ के दिए गए अनुमानित मान के साथ और मोटे तौर पर यह मानते हुए कि मॉडल का अनुमान लगाने के लिए आवश्यक एन अंक स्वतंत्र रूप से चुने गए हैं (यह एक मोटा अनुमान है क्योंकि प्रत्येक डेटा बिंदु चयन वास्तविकता में अगले चयन में चुनने के लिए डेटा बिंदु उम्मीदवारों की संख्या कम कर देता है), $w^{n}$ प्रायिकता है कि सभी n बिंदु अंतर्निहित हैं और $1-w^{n}$ संभावना है कि n बिंदुओं में से कम से कम एक एक बाहरी है, एक ऐसी स्थिति जिसका अर्थ है कि इस बिंदु सेट से एक खराब मॉडल का अनुमान लगाया जाएगा। k की घात (एल्गोरिथ्म को चलाने में पुनरावृत्तियों की संख्या) की वह संभावना यह है कि एल्गोरिथम कभी भी n बिंदुओं के एक सेट का चयन नहीं करता है, जो सभी इनलाइनर्स हैं, और यह $1-p$ के समान है (संभावना है कि एल्गोरिदम एक सफल मॉडल अनुमान में परिणत नहीं होता है)। फलस्वरूप,

$1-p=(1-w^{n})^{k}\,$

जो दोनों पक्षों का लघुगणक लेने के बाद होता है;

$k={\frac {\log(1-p)}{\log(1-w^{n})}}$

यह परिणाम मानता है कि n डेटा बिंदुओं को स्वतंत्र रूप से चुना गया है, अर्थात, एक बिंदु जिसे एक बार चुना गया है उसे बदल दिया गया है और उसी पुनरावृत्ति में फिर से चुना जा सकता है। यह प्रायः एक उचित दृष्टिकोण नहीं है और k के लिए व्युत्पन्न मान को उस स्थिति में ऊपरी सीमा के रूप में लिया जाना चाहिए जब बिंदुओं को प्रतिस्थापन के बिना चुना जाता है। उदाहरण के लिए, ऊपर दिए गए चित्र में दर्शाए गए डेटा सेट में फिट होने वाली रेखा ढूंढने की स्थिति में, आरएएनएसएसी एल्गोरिदम सामान्यतः प्रत्येक पुनरावृत्ति में दो बिंदुओं को चुनता है और बिंदुओं के मध्य की रेखा के रूप में maybe_model की गणना करता है और फिर यह महत्वपूर्ण है कि दोनों बिंदु अलग-अलग हों।

अतिरिक्त आत्मविश्वास हासिल करने के लिए, मानक विचलन या उसके गुणकों को k में जोड़ा जा सकता है। k के मानक विचलन को इस प्रकार परिभाषित किया गया है

$\operatorname {SD} (k)={\frac {\sqrt {1-w^{n}}}{w^{n}}}$

लाभ और हानि

आरएएनएसएसी का एक लाभ मॉडल मापदंडों का प्रबल अनुमान करने की इसकी क्षमता है, अर्थात, यह डेटा सेट में महत्वपूर्ण संख्या में आउटलेर्स उपस्थित होने पर भी उच्च सटीकता के साथ मापदंडों का अनुमान लगा सकता है। आरएएनएसएसी की एक हानि यह है कि इन मापदंडों की गणना करने में लगने वाले समय की कोई ऊपरी सीमा नहीं है (निष्कासन को छोड़कर)। जब गणना की गई पुनरावृत्तियों की संख्या सीमित होती है तो प्राप्त समाधान इष्टतम नहीं हो सकता है, और यह ऐसा भी नहीं हो सकता है जो डेटा को अच्छे तरीके से फिट करता हो। इस तरह आरएएनएसएसी एक समझौते की प्रस्तुति करता है; अधिक संख्या में पुनरावृत्तियों की गणना करने से एक उचित मॉडल तैयार होने की संभावना बढ़ जाती है। इसके अतिरिक्त, आरएएनएसएसी सदैव मध्यम रूप से दूषित सेटों के लिए भी इष्टतम सेट ढूंढने में सक्षम नहीं होता है और यह सामान्यतः खराब प्रदर्शन करता है जब इनलियर्स की संख्या 50% से कम होती है। इष्टतम आरएएनएसएसी को इन दोनों समस्याओं से निपटने के लिए प्रस्तावित किया गया था और यह अत्यधिक दूषित सेटों के लिए इष्टतम सेट खोजने में सक्षम है, यहां तक ​​कि 5% से कम के आंतरिक अनुपात के लिए भी है। आरएएनएसएसी की एक और हानि यह है कि इसमें समस्या-विशिष्ट सीमाएँ निर्धारित करने की आवश्यकता होती है।

आरएएनएसएसी किसी विशेष डेटा सेट के लिए केवल एक मॉडल का अनुमान लगा सकता है। जहां तक ​​किसी एक-मॉडल दृष्टिकोण की बात है, जब दो (या अधिक) मॉडल इंस्टेंस उपस्थित हों, तो आरएएनएसएसी किसी एक को भी ढूंढने में विफल हो सकता है। हफ़ ट्रांसफ़ॉर्म एक वैकल्पिक प्रबल अनुमान तकनीक है जो एक से अधिक मॉडल उदाहरण उपस्थित होने पर उपयोगी हो सकती है। मल्टी मॉडल फिटिंग के लिए एक अन्य दृष्टिकोण को पर्ल के नाम से जाना जाता है। जो आरएएनएसएसी में डेटा बिंदुओं से मॉडल सैंपलिंग को इनलियर्स के पुनरावृत्तीय पुन: आकलन के साथ जोड़ती है और समग्र समाधान की गुणवत्ता का वर्णन करने वाले वैश्विक ऊर्जा फ़ंक्शन के साथ एक अनुकूलन समस्या के रूप में मल्टी-मॉडल फिटिंग तैयार किया जाता है।

ऍप्लिकेशन

आरएएनएसएसी एल्गोरिथ्म का उपयोग प्रायः कंप्यूटर विज़न में किया जाता है, उदाहरण के लिए, पत्राचार समस्या को एक साथ हल करने और स्टीरियो कैमरों की एक जोड़ी से संबंधित मौलिक मैट्रिक्स का अनुमान लगाने के लिए; यह भी देखें: गति से संरचना, स्केल-अपरिवर्तनीय सुविधा परिवर्तन, इमेज स्टिचिंग, करिजिड मोशन सेगमेंटेशन है।

विकास और सुधार

1981 से आरएएनएसएसी कंप्यूटर विज़न और इमेज प्रोसेसिंग समुदाय में एक मौलिक उपकरण बन गया है। 2006 में, एल्गोरिथम की 25वीं वर्षगांठ के लिए, मूल एल्गोरिथम में नवीनतम योगदानों और विविधताओं को संक्षेप में प्रस्तुत करने के लिए कंप्यूटर विज़न और पैटर्न रिकॉग्निशन (CVPR) पर अंतर्राष्ट्रीय सम्मेलन में एक कार्यशाला का आयोजन किया गया था, जिसका मुख्य उद्देश्य एल्गोरिथम की गति में सुधार करना था, अनुमानित समाधान की प्रबलता और सटीकता और उपयोगकर्ता परिभाषित स्थिरांक से निर्भरता को कम करना था।

आरएएनएसएसी शुद्ध रव सीमा के चयन के प्रति संवेदनशील हो सकता है जो परिभाषित करता है कि कौन से डेटा बिंदु मापदंडों के एक निश्चित समुच्चय के साथ तत्काल मॉडल में फिट होते हैं। यदि ऐसी सीमा बहुत बड़ी है, तो सभी परिकल्पनाओं को समान (अच्छा) क्रम दिया जाता है। दूसरी ओर, जब रव सीमा बहुत छोटी होती है, तो अनुमानित मापदंड अस्थिर हो जाते हैं (अर्थात केवल इनलियर्स के समुच्चय में डेटा जोड़ने या हटाने से, मापदंड के अनुमान में बदल सकता है)। इस अवांछनीय प्रभाव के लिए आंशिक रूप से क्षतिपूर्ति करने के लिए, टॉर एट अल ने आरएएनएसएसी के दो संशोधन प्रस्तावित हैं जिन्हें एमएसएसी (M-आकलनकर्ता सैंपल और सर्वसम्मति) और एमएलईएसएसी (अधिकतम संभावना अनुमान सैंपल और सर्वसम्मति) कहा जाता है। मुख्य विचार सर्वसम्मति समुच्चय की गुणवत्ता का मूल्यांकन करना है (अर्थात वह डेटा जो एक मॉडल और मापदंडों के एक निश्चित समुच्चय में फिट बैठता है) इसकी संभावना की गणना करना (जबकि फिशलर और बोल्स द्वारा मूल सूत्रीकरण में क्रम ऐसे समुच्चय की गणनांक थी)। एमएलईएसएसी का एक विस्तार जो इनपुट डाटासेट से जुड़ी पूर्व संभावनाओं को ध्यान में रखता है, टॉर्डॉफ द्वारा प्रस्तावित है। परिणामी एल्गोरिदम को निर्देशित-एमएलईएसएसी नाम दिया गया है। समान पंक्तियों के साथ, चुम ने नमूनाकरण प्रक्रिया का मार्गदर्शन करने का प्रस्ताव दिया यदि इनपुट डेटा के संबंध में कुछ प्राथमिक जानकारी ज्ञात हो, अर्थात कि क्या डेटाम इनलायर या आउटलायर होने की संभावना है। प्रस्तावित दृष्टिकोण को पीआरओएसएसी, प्रगतिशील सैंपल सहमति कहा जाता है।

चुम एट अल. एक अच्छे सर्वसम्मति सेट की पहचान करने के लिए कम्प्यूटेशनल बोझ को कम करने के लिए आर-आरएएनएसएसी नामक आरएएनएसएसी का एक यादृच्छिक संस्करण भी प्रस्तावित किया गया। मूल विचार यह है कि प्रारंभ में संपूर्ण डेटासेट के बजाय केवल कम अंकों के सेट का उपयोग करके वर्तमान इंस्टेंटियेटेड मॉडल की अच्छाई का मूल्यांकन किया जाए। एक ठोस रणनीति उच्च आत्मविश्वास के साथ बताएगी कि संपूर्ण डेटासेट की फिटिंग का मूल्यांकन करने की स्थिति कब है या मॉडल को सरलता से त्यक्त किया जा सकता है। यह सोचना उचित है कि इस दृष्टिकोण का प्रभाव उन स्थितियों में अधिक प्रासंगिक है जहां इनलियर्स का प्रतिशत बड़ा है। चुम एट अल द्वारा प्रस्तावित रणनीति का प्रकार प्रीएम्प्शन स्कीम कहलाती है। निस्टर ने प्रीमेप्टिव आरएएनएसएसी नामक एक प्रतिमान का प्रस्ताव रखा जो किसी दृश्य की संरचना और कैमरे की गति का वास्तविक समय में प्रबल अनुमान लगाने की अनुमति देता है। दृष्टिकोण का मुख्य विचार एक निश्चित संख्या में परिकल्पना उत्पन्न करना है ताकि तुलना कुछ पूर्ण गुणवत्ता मीट्रिक के बजाय उत्पन्न परिकल्पना की गुणवत्ता के संबंध में हो।

अन्य शोधकर्ताओं ने उन कठिन परिस्थितियों से निपटने का प्रयास किया जहां रव पैमाना ज्ञात नहीं है और/या कई मॉडल उदाहरण उपस्थित हैं। पहली समस्या का समाधान वांग और स्यूटर द्वारा किया गया है। टोल्डो एट अल. बिंदु पर उपयुक्त होने वाले यादृच्छिक मॉडल के समुच्चय के विशिष्ट कार्य के साथ प्रत्येक डेटाम का प्रतिनिधित्व करें। फिर कई मॉडल क्लस्टर के रूप में सामने आते हैं जो एक ही मॉडल का समर्थन करने वाले बिंदुओं को समूहित करते हैं। क्लस्टरिंग एल्गोरिदम, जिसे जे-लिंकेज कहा जाता है, जिनको मॉडलों की संख्या के पूर्व विनिर्देश की आवश्यकता नहीं होती है, न ही इसे मैन्युअल मापदंड ट्यूनिंग की आवश्यकता होती है।

आरएएनएसएसी को पुनरावर्ती अवस्था अनुमान अनुप्रयोगों के लिए भी तैयार किया गया है, जहां इनपुट माप आउटलेर्स द्वारा दूषित हो जाते हैं और कलमन फ़िल्टर दृष्टिकोण, जो माप त्रुटि के गॉसियन वितरण पर निर्भर होते हैं, विफल होने के लिए अभिशप्त होते हैं। इस तरह के दृष्टिकोण को केएएलएमएएनएसएसी कहा जाता है।

संबंधित विधियाँ

• एमएलईएसएसी (अधिकतम संभावना अनुमान सैंपल सर्वसम्मति) - इस संभावना को अधिकतम करता है कि डेटा सैंपल-फिट मॉडल से उत्पन्न हुआ था, उदाहरण के लिए, इनलियर्स और आउटलेर्स का मिश्रण मॉडल है।
• एमएपीएसएसी (अधिकतम पोस्टीरियर सैंपल सर्वसम्मति) - उपयुक्त किए जाने वाले मापदंडों की पूर्व संभावना को सम्मिलित करने के लिए एमएलईएसएसी का विस्तार करता है और पोस्टीरियर संभावना को अधिकतम करता है।
• केएएलएमएएनएसएसी - एक गतिशील प्रणाली की स्थिति का कारण अनुमान है।
• पुन: नमूनाकरण (सांख्यिकी)
• हॉप-डिफ्यूजन मोंटे कार्लो बहुत व्यापक-बेसलाइन छवियों के मध्य एपिपोलर ज्यामिति अनुमान के लिए आरएएनएसएसी के प्रत्येक चरण पर नमूना चुनने के लिए यादृच्छिक नमूनाकरण का उपयोग करता है जिसमें वैश्विक जंप और स्थानीय प्रसार सम्मिलित होता है।

यह भी देखें

• हफ ट्रांसफॉर्म

संदर्भ

• Martin A. Fischler & Robert C. Bolles (June 1981). "Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography" (PDF). Comm. ACM. 24 (6): 381–395. doi:10.1145/358669.358692. S2CID 972888. Archived (PDF) from the original on December 10, 2014.
• David A. Forsyth & Jean Ponce (2003). Computer Vision, a modern approach. Prentice Hall. ISBN 978-0-13-085198-7.
• Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in Computer Vision (2nd ed.). Cambridge University Press.
• Strutz, T. (2016). Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). 2nd edition, Springer Vieweg. ISBN 978-3-658-11455-8.
• P.H.S. Torr & D.W. Murray (1997). "The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix". International Journal of Computer Vision. 24 (3): 271–300. doi:10.1023/A:1007927408552. S2CID 12031059.
• Ondrej Chum (2005). "Two-View Geometry Estimation by Random Sample and Consensus" (PDF). PhD Thesis.
• Sunglok Choi; Taemin Kim & Wonpil Yu (2009). "Performance Evaluation of RANSAC Family" (PDF). In Proceedings of the British Machine Vision Conference (BMVC).

• Anders Hast; Johan Nysjö; Andrea Marchetti (2013). "Optimal RANSAC – Towards a Repeatable Algorithm for Finding the Optimal Set" (PDF). Journal of WSCG. 21 (1): 21–30.
• Hossam Isack; Yuri Boykov (2012). "Energy-based Geometric Multi-Model Fitting" (PDF). International Journal of Computer Vision. 97 (2: 1): 23–147. CiteSeerX 10.1.1.381.2434. doi:10.1007/s11263-011-0474-7. S2CID 5461268.