डिवाइड-और-कॉन्कर आइजेनवैल्यू एल्गोरिदम

डिवाइड-और-कॉन्कर अभिलक्षणिक मान एल्गोरिदम हर्मिटियन या वास्तविक सममित मैट्रिक्स के लिए अभिलक्षणिक मान एल्गोरिदम का एक वर्ग है जो हाल ही में (लगभग 1990 के दशक में) क्यूआर (QR) एल्गोरिदम जैसे अधिक पारंपरिक एल्गोरिदम के साथ स्थिरता और दक्षता की स्थिति में प्रतिस्पर्धी बन गया है। इन एल्गोरिदम के पीछे मूल अवधारणा कंप्यूटर विज्ञान से डिवाइड और कॉन्कर दृष्टिकोण है। अभिलक्षणिक मान प्रश्न को लगभग आधे आकार के दो प्रश्नों में विभाजित किया जाता है, इनमें से प्रत्येक को पुनरावर्ती रूप से हल किया जाता है, और मूल प्रश्न के अभिलक्षणिक मानों ​​की गणना इन छोटे प्रश्नों के परिणामों से की जाती है।

यहां हम डिवाइड और कॉन्कर एल्गोरिदम का सबसे सरल संस्करण प्रस्तुत करते हैं, जो मूल रूप से 1981 में क्यूपेन द्वारा प्रस्तावित एल्गोरिदम के समान है। इस लेख के क्षेत्र से बाहर उपस्थित कई विवरण छोड़ दिए जाएंगे हालाँकि, इन विवरणों पर विचार किए बिना, एल्गोरिथ्म पूरी तरह से स्थिर नहीं है।

पृष्ठभूमि

हर्मिटियन मैट्रिक्स के लिए अधिकांश आइगेनवैल्यू एल्गोरिदम की तरह, विभाजित करें और जीतें त्रिविकर्णीय मैट्रिक्स फॉर्म में कमी के साथ शुरू होती है। एक के लिए $m\times m$ मैट्रिक्स, इसके लिए मानक विधि, गृहस्थ प्रतिबिंब के माध्यम से लेती है ${\frac {4}{3}}m^{3}$ फ़्लोटिंग पॉइंट ऑपरेशंस, या ${\frac {8}{3}}m^{3}$ यदि eigenvectors की भी आवश्यकता है। अन्य एल्गोरिदम हैं, जैसे कि अर्नोल्डी पुनरावृत्ति, जो मैट्रिक्स के कुछ वर्गों के लिए बेहतर प्रदर्शन कर सकते हैं; हम यहां इस पर आगे विचार नहीं करेंगे।

कुछ मामलों में, एक eigenvalue समस्या को छोटी समस्याओं में विभाजित करना संभव है। एक ब्लॉक विकर्ण मैट्रिक्स पर विचार करें

$T={\begin{bmatrix}T_{1}&0\\0&T_{2}\end{bmatrix}}.$

के eigenvalues ​​​​और eigenvectors $T$ बस वे हैं $T_{1}$ और $T_{2}$, और मूल समस्या को एक साथ हल करने की तुलना में इन दो छोटी समस्याओं को हल करना लगभग हमेशा तेज़ होगा। इस तकनीक का उपयोग कई आइगेनवैल्यू एल्गोरिदम की दक्षता में सुधार करने के लिए किया जा सकता है, लेकिन इसका फूट डालो और जीतो के लिए विशेष महत्व है।

इस आलेख के शेष भाग के लिए, हम मान लेंगे कि फूट डालो और जीतो एल्गोरिथ्म का इनपुट एक है $m\times m$ वास्तविक सममित त्रिविकर्ण मैट्रिक्स $T$. हालाँकि एल्गोरिदम को हर्मिटियन मैट्रिक्स के लिए संशोधित किया जा सकता है, हम यहां विवरण नहीं देते हैं।

विभाजन

फूट डालो और जीतो एल्गोरिथ्म का विभाजन भाग इस अहसास से आता है कि एक त्रिविकर्ण मैट्रिक्स लगभग ब्लॉक विकर्ण है।

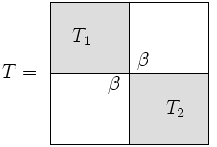सबमैट्रिक्स का आकार $T_{1}$ हम कॉल करेंगे $n\times n$, और तब $T_{2}$ है $(m-n)\times (m-n)$. ध्यान दें कि टिप्पणी के बारे में $T$ लगभग ब्लॉक विकर्ण होना सत्य है, चाहे कुछ भी हो $n$ चुना गया है (यानी, मैट्रिक्स को विघटित करने के कई तरीके हैं)। हालाँकि, दक्षता के दृष्टिकोण से, इसे चुनना उचित है $n\approx m/2$.

हम लिखते हैं $T$ एक ब्लॉक विकर्ण मैट्रिक्स के रूप में, साथ ही एक रैंक (रैखिक बीजगणित)|रैंक-1 सुधार:

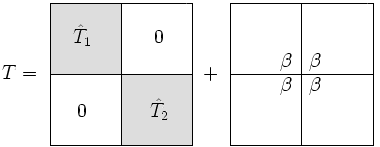के बीच एकमात्र अंतर है $T_{1}$ और ${\hat {T}}_{1}$ क्या वह निचली दाहिनी प्रविष्टि है $t_{nn}$ में ${\hat {T}}_{1}$ से प्रतिस्थापित कर दिया गया है $t_{nn}-\beta$ और इसी तरह, में ${\hat {T}}_{2}$ शीर्ष बाईं प्रविष्टि $t_{n+1,n+1}$ से प्रतिस्थापित कर दिया गया है $t_{n+1,n+1}-\beta$.

विभाजन चरण का शेष भाग eigenvalues ​​​​(और यदि वांछित हो तो eigenvectors) के लिए हल करना है ${\hat {T}}_{1}$ और ${\hat {T}}_{2}$, अर्थात् विकर्णीय मैट्रिक्स को खोजना ${\hat {T}}_{1}=Q_{1}D_{1}Q_{1}^{T}$ और ${\hat {T}}_{2}=Q_{2}D_{2}Q_{2}^{T}$. इसे डिवाइड-एंड-कॉन्कर एल्गोरिदम में पुनरावर्ती कॉल के साथ पूरा किया जा सकता है, हालांकि व्यावहारिक कार्यान्वयन अक्सर छोटे पर्याप्त सबमैट्रिसेस के लिए क्यूआर एल्गोरिदम पर स्विच करते हैं।

विजय

एल्गोरिथम का विजय भाग अबोधगम्य भाग है। ऊपर परिकलित उपमैट्रिक्स के विकर्णीकरण को देखते हुए, हम मूल मैट्रिक्स का विकर्णीकरण कैसे ज्ञात कर सकते हैं?

सबसे पहले, परिभाषित करें $z^{T}=(q_{1}^{T},q_{2}^{T})$, कहाँ $q_{1}^{T}$ की अंतिम पंक्ति है $Q_{1}$ और $q_{2}^{T}$ की पहली पंक्ति है $Q_{2}$. यह दिखाना अब प्राथमिक है

$T={\begin{bmatrix}Q_{1}&\\&Q_{2}\end{bmatrix}}\left({\begin{bmatrix}D_{1}&\\&D_{2}\end{bmatrix}}+\beta zz^{T}\right){\begin{bmatrix}Q_{1}^{T}&\\&Q_{2}^{T}\end{bmatrix}}$

शेष कार्य को एक विकर्ण मैट्रिक्स के eigenvalues ​​​​और रैंक-एक सुधार को खोजने के लिए कम कर दिया गया है। यह कैसे करना है यह दिखाने से पहले, आइए अंकन को सरल बनाएं। हम मैट्रिक्स के eigenvalues ​​​​की तलाश कर रहे हैं $D+ww^{T}$, कहाँ $D$ अलग-अलग प्रविष्टियों के साथ विकर्ण है और $w$ शून्येतर प्रविष्टियों वाला कोई सदिश है।

शून्य प्रविष्टि का मामला सरल है, क्योंकि यदि w_i शून्य है, ($e_{i}$,डी_i) एक अपनी जोड़ी है ($e_{i}$ के मानक आधार में है) $D+ww^{T}$ तब से $(D+ww^{T})e_{i}=De_{i}=d_{i}e_{i}$.

अगर $\lambda$ एक eigenvalue है, हमारे पास है:

$(D+ww^{T})q=\lambda q$

कहाँ $q$ संगत eigenvector है। अब

$(D-\lambda I)q+w(w^{T}q)=0$

$q+(D-\lambda I)^{-1}w(w^{T}q)=0$

$w^{T}q+w^{T}(D-\lambda I)^{-1}w(w^{T}q)=0$

ध्यान रखें कि $w^{T}q$ एक शून्येतर अदिश राशि है. कोई भी नहीं $w$ और न $q$ शून्य हैं. अगर $w^{T}q$ शून्य होना था, $q$ का एक eigenvector होगा $D$ द्वारा $(D+ww^{T})q=\lambda q$. यदि ऐसा होता, $q$ तब से केवल एक गैर-शून्य स्थिति शामिल होगी $D$ अलग विकर्ण है और इस प्रकार आंतरिक उत्पाद है $w^{T}q$ आख़िरकार शून्य नहीं हो सकता. इसलिए, हमारे पास है:

$1+w^{T}(D-\lambda I)^{-1}w=0$

या अदिश समीकरण के रूप में लिखा गया है,

$1+\sum _{j=1}^{m}{\frac {w_{j}^{2}}{d_{j}-\lambda }}=0.$

इस समीकरण को धर्मनिरपेक्ष समीकरण के नाम से जाना जाता है। इसलिए समस्या को इस समीकरण के बाईं ओर द्वारा परिभाषित तर्कसंगत फ़ंक्शन की जड़ों को खोजने तक सीमित कर दिया गया है।

सभी सामान्य eigenvalue एल्गोरिदम पुनरावृत्त होने चाहिए, और फूट डालो और जीतो एल्गोरिदम अलग नहीं है। अरेखीय धर्मनिरपेक्ष समीकरण को हल करने के लिए एक पुनरावृत्तीय तकनीक की आवश्यकता होती है, जैसे न्यूटन की विधि|न्यूटन-रेफसन विधि। हालाँकि, प्रत्येक रूट को बिग ओ अंकन (1) पुनरावृत्तियों में पाया जा सकता है, जिनमें से प्रत्येक की आवश्यकता होती है $\Theta (m)$ फ्लॉप (एक के लिए) $m$-डिग्री तर्कसंगत फ़ंक्शन), इस एल्गोरिदम के पुनरावृत्त भाग की लागत बनाता है $\Theta (m^{2})$.

विश्लेषण

जैसा कि फूट डालो और जीतो एल्गोरिदम के लिए आम है, हम चल रहे समय का विश्लेषण करने के लिए मास्टर प्रमेय (एल्गोरिदम का विश्लेषण) | फूट डालो और जीतो पुनरावृत्ति के लिए मास्टर प्रमेय का उपयोग करेंगे। याद रखें कि ऊपर हमने कहा था कि हम चुनते हैं $n\approx m/2$. हम पुनरावृत्ति संबंध लिख सकते हैं:

$T(m)=2\times T\left({\frac {m}{2}}\right)+\Theta (m^{2})$

मास्टर प्रमेय के अंकन में, $a=b=2$ और इस तरह $\log _{b}a=1$. स्पष्ट रूप से, $\Theta (m^{2})=\Omega (m^{1})$, तो हमारे पास

$T(m)=\Theta (m^{2})$

याद रखें कि ऊपर हमने बताया था कि हर्मिटियन मैट्रिक्स को त्रिविकर्ण रूप में कम करना होता है ${\frac {4}{3}}m^{3}$ फ्लॉप. यह फूट डालो और जीतो भाग के चलने के समय को कम कर देता है, और इस बिंदु पर यह स्पष्ट नहीं है कि फूट डालो और जीतो एल्गोरिथ्म QR एल्गोरिथ्म पर क्या लाभ प्रदान करता है (जो कि लेता भी है) $\Theta (m^{2})$ त्रिविकर्ण आव्यूहों के लिए फ़्लॉप)।

फूट डालो और राज करो का लाभ तब मिलता है जब आइजनवेक्टर की भी आवश्यकता होती है। यदि यह मामला है, तो त्रिविकर्ण रूप में कमी आती है ${\frac {8}{3}}m^{3}$, लेकिन एल्गोरिथ्म का दूसरा भाग लेता है $\Theta (m^{3})$ भी। उचित लक्ष्य परिशुद्धता वाले क्यूआर एल्गोरिदम के लिए, यह है $\approx 6m^{3}$, जबकि फूट डालो और राज करो के लिए यह है $\approx {\frac {4}{3}}m^{3}$. इस सुधार का कारण यह है कि फूट डालो और राज करो में $\Theta (m^{3})$ एल्गोरिथम का भाग (गुणा करना)। $Q$ मैट्रिक्स) पुनरावृत्ति से अलग है, जबकि क्यूआर में, यह प्रत्येक पुनरावृत्ति चरण में होना चाहिए। जोड़ रहा हूँ ${\frac {8}{3}}m^{3}$ कमी के लिए फ्लॉप, कुल सुधार से है $\approx 9m^{3}$ को $\approx 4m^{3}$ फ्लॉप.

फूट डालो और जीतो एल्गोरिदम के व्यावहारिक उपयोग से पता चला है कि अधिकांश यथार्थवादी आइगेनवैल्यू समस्याओं में, एल्गोरिदम वास्तव में इससे बेहतर काम करता है। इसका कारण यह है कि बहुत बार मैट्रिक्स $Q$ और वेक्टर $z$ संख्यात्मक रूप से विरल होते हैं, जिसका अर्थ है कि उनके पास तैरनेवाला स्थल परिशुद्धता से छोटे मानों वाली कई प्रविष्टियाँ हैं, जो संख्यात्मक अपस्फीति की अनुमति देती हैं, यानी समस्या को अयुग्मित उप-समस्याओं में तोड़ देती हैं।

विकल्प और कार्यान्वयन

यहां प्रस्तुत एल्गोरिदम सबसे सरल संस्करण है। कई व्यावहारिक कार्यान्वयन में, स्थिरता की गारंटी के लिए अधिक जटिल रैंक-1 सुधारों का उपयोग किया जाता है; कुछ वैरिएंट रैंक-2 सुधारों का भी उपयोग करते हैं।

तर्कसंगत कार्यों के लिए विशेष रूट-खोज तकनीकें मौजूद हैं जो प्रदर्शन और स्थिरता दोनों के मामले में न्यूटन-रैपसन पद्धति से बेहतर कर सकती हैं। इनका उपयोग फूट डालो और जीतो एल्गोरिथ्म के पुनरावृत्त भाग को बेहतर बनाने के लिए किया जा सकता है।

फूट डालो और जीतो एल्गोरिथ्म आसानी से समानांतर एल्गोरिदम है, और LAPACK जैसे रैखिक बीजगणित कंप्यूटिंग पैकेज में उच्च गुणवत्ता वाले समानांतर कार्यान्वयन होते हैं।

संदर्भ

• Demmel, James W. (1997), Applied Numerical Linear Algebra, Philadelphia, PA: Society for Industrial and Applied Mathematics, ISBN 0-89871-389-7, MR 1463942.
• Cuppen, J.J.M. (1981). "A Divide and Conquer Method for the Symmetric Tridiagonal Eigenproblem". Numerische Mathematik. 36 (2): 177–195. doi:10.1007/BF01396757. S2CID 120504744.