बंडल मानचित्र
गणित में, बंडल मानचित्र फाइबर बंडल (तन्तु गठरी) की श्रेणी में एक आकारिता होता है। इसके दो अलग-अलग, परंतु मजबूत रूप में संबंधित, बंडल मानचित्र के भाव होते हैं, जो इस पर निर्भर करते हैं कि क्या सवाल में दिए गए फाइबर बंडलों के पास एक सामान्य आधार समष्टि है। इसके अतिरिक्त, यह केवल उपलब्ध फाइबर बंडलों की कौन सी श्रेणी पर विचार किया जा रहा है, इसके आधार पर कई विभिन्न रूपांतरण हैं। पहले तीन खंडों में, हम संस्थानिक समष्टियो की श्रेणी में सामान्य फाइबर बंडलों को विचार करेंगे। पुनः चौथे खंड में, कुछ अन्य उदाहरण दिए जाएंगे।
सामान्य आधार के ऊपर बंडल मानचित्र
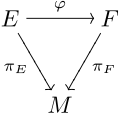
यदि और एक स्थान M पर फाइबर बंडल हों, तो एक बंडल मानचित्र 'E' से 'F' 'पर 'M' के लिए एक नियमित मानचित्र होती है जिसका पालमूल माना जाता है। अर्थात, यह आरेख होता है:
समघटक आरेख परिपथ में सहेजता है। समतुल्य रूप से, किसी भी बिंदु x के लिए, नियमित मानचित्र के बिंदु को बिंदु परिपथ में आरेखित करता है।
रेशा बंडलों की सामान्य आकृतियाँ
यदि और स्थानों M और N पर फाइबर बंडल हों, तो एक नियमित नक्शा एक बंडल मानचित्र कहलाता है अगर एक ऐसा नियमित नक्शा हो जिससे चित्रण होता है:
समतुल्यता का चित्रण, अर्थात् होता है। दूसरे शब्दों में, फाइबर-संरक्षणकारी होता है, और f E के फाइबरों की जगह के नक्शे पर उत्पन्न होने वाला मानचित्र होता है: क्योंकि प्रतिकूलक होता है, इसलिए द्वारा अनुबंधित किया जाता है। एक दिए गए f के लिए, ऐसा एक बंडल मानचित्र कहलाता है जिसे फाइबर कवरिंग f'कहा जाता है।
दो धारणाओं के बीच संबंध
परिभाषाओं से सीधे रूप में यह पाया जा सकता है कि M पर एक बंडल मानचित्र पहले मान में वही बात है जो M के पहचान मानचित्र को कवर करता है।
विपरीत रूप से, सामान्य बंडल मानचित्र को निश्चित आधार अंतर्वाहन के उपयोग से एक मुख्य आधार स्थल पर बंडल मानचित्र में घटाया जा सकता है, जिसकी विन्यासिकता की नोटियन के द्वारा होता है। यदि एक फाइबर बंडल N पर हो और एक नियमित मान हो, तो "f की पुलबैक" F का एक फाइबर बंडल M पर होता है जिसका फाइबर x पर इस प्रकार होता है (f*F)x = Ff(x)। यहाँ तक पहुँचा जाता है कि एक M पर f की कवरिंग वाला बंडल मानचित्र E से F की तरह कुछ होने के बराबर है।
विकल्प और सामान्यीकरण
बंडल मानचित्र की सामान्य अवधारणा में दो प्रकार की भिन्नताएँ हैं।
"पहले, व्यक्तियों की अलग श्रेणी में रेशा बंडल का विचार किया जा सकता है। इससे, उदाहरण के लिए, स्मूथ मानचित्र के ऊपर स्मूथ रेशा बंडलों के बीच एक स्मूथ बंडल मानचित्र के धारणा तक पहुंचा जाता है।"
दूसरा, हम फाइबरों में अतिरिक्त संरचना वाले फाइबर बंडल को भी विचार कर सकते हैं, और केवल उन बंडल मानचित्र पर ध्यान केंद्रित कर सकते हैं जो इस संरचना को संरक्षित रखते हैं। इससे, उदाहरण के लिए, बंडल होमोमॉर्फिज्म की धारणा आती है जिसमें फाइबर विभाग सदिश समष्टि होते हैं, और एक बंडल मानचित्र φ को हर फाइबर पर एक रैखिक मानचित्र माना जाता है। इस स्थिति में, ऐसे एक बंडल मानचित्र φ को व्यूह भी देखा जा सकता है जो बिंदु व्यूह Hom(E,f*F) के एक अनुच्छेद के रूप में समझा जा सकता है, जिसका बिंदु व्यूह होम (Ex,Ff(x)) (जिसे L(Ex,Ff(x)) भी लिखा जाता है) होता है, जो Ex से Ff(x) की रैखिक मानचित्र होते हैं।