घातीय प्रकार

For exponential types in type theory and programming languages, see Function type.

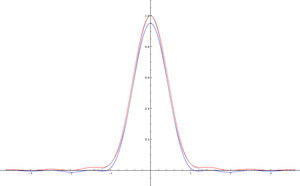
फ़ंक्शन का ग्राफ ग्रे रंग में है $e^{-\pi z^{2}}$, गाऊसी वास्तविक अक्ष तक ही सीमित है। फिर गॉसियन में घातीय प्रकार नहीं होता है, लेकिन लाल और नीले रंग में कार्य एक तरफा सन्निकटन होते हैं जिनमें घातांक प्रकार होता है $2\pi$.

जटिल विश्लेषण में, गणित की एक शाखा, एक होलोमोर्फिक फ़ंक्शन को घातीय प्रकार सी का कहा जाता है यदि इसकी वृद्धि घातीय फ़ंक्शन द्वारा सीमित होती है $e^{C|z|}$ किसी वास्तविक संख्या के लिए|वास्तविक-मूल्यवान स्थिरांक $C$ जैसा $|z|\to \infty$. जब कोई फ़ंक्शन इस तरह से घिरा होता है, तो इसे अन्य जटिल कार्यों की श्रृंखला पर कुछ प्रकार के अभिसरण योगों के रूप में व्यक्त करना संभव होता है, साथ ही यह समझना भी संभव होता है कि बोरेल योग जैसी तकनीकों को लागू करना कब संभव है, या, उदाहरण के लिए , मध्य परिवर्तन को लागू करने के लिए, या यूलर-मैकलॉरिन फॉर्मूला का उपयोग करके सन्निकटन करने के लिए। सामान्य मामले को नचबिन के प्रमेय द्वारा नियंत्रित किया जाता है, जो समान धारणा को परिभाषित करता है$\Psi$-एक सामान्य कार्य के लिए टाइप करें $\Psi (z)$ विरोध के रूप में $e^{z}$.

बुनियादी विचार

एक समारोह $f(z)$ यदि वास्तविक-मूल्यवान स्थिरांक मौजूद हैं तो जटिल विमान पर परिभाषित को घातीय प्रकार का कहा जाता है $M$ और $\tau$ ऐसा है कि

$\left|f\left(re^{i\theta }\right)\right|\leq Me^{\tau r}$

की सीमा में $r\to \infty$. यहाँ, जटिल चर $z$ के रूप में लिखा गया था $z=re^{i\theta }$ इस बात पर ज़ोर देना कि सीमा सभी दिशाओं में कायम रहनी चाहिए $\theta$. दे $\tau$ ऐसे सभी के न्यूनतम के लिए खड़े रहें $\tau$, तो कोई कहता है कि function $f$ घातीय प्रकार का है $\tau$.

उदाहरण के लिए, चलो $f(z)=\sin(\pi z)$. फिर कोई कहता है $\sin(\pi z)$ घातीय प्रकार का है $\pi$, तब से $\pi$ वह सबसे छोटी संख्या है जो विकास को सीमित करती है $\sin(\pi z)$ काल्पनिक अक्ष के साथ. इसलिए, इस उदाहरण के लिए, कार्लसन का प्रमेय लागू नहीं हो सकता, क्योंकि इसके लिए इससे कम घातीय प्रकार के कार्यों की आवश्यकता होती है $\pi$. इसी तरह, यूलर-मैकलॉरिन फॉर्मूला भी लागू नहीं किया जा सकता है, क्योंकि यह भी एक प्रमेय को व्यक्त करता है जो अंततः परिमित अंतर के सिद्धांत में निहित है।

औपचारिक परिभाषा

एक होलोमोर्फिक फ़ंक्शन $F(z)$ घातीय प्रकार का कहा जाता है $\sigma >0$ यदि प्रत्येक के लिए $\varepsilon >0$ वहाँ एक वास्तविक-मूल्यवान स्थिरांक मौजूद है $A_{\varepsilon }$ ऐसा है कि

$|F(z)|\leq A_{\varepsilon }e^{(\sigma +\varepsilon )|z|}$

के लिए $|z|\to \infty$ कहाँ $z\in \mathbb {C}$. हम कहते हैं $F(z)$ यदि घातीय प्रकार का है $F(z)$ घातीय प्रकार का है $\sigma$ कुछ के लिए $\sigma >0$. जो नंबर

$\tau (F)=\sigma =\displaystyle \limsup _{|z|\rightarrow \infty }|z|^{-1}\log |F(z)|$

का घातीय प्रकार है $F(z)$. यहां श्रेष्ठ सीमा का मतलब किसी दिए गए त्रिज्या के बाहर अनुपात के सर्वोच्च की सीमा है क्योंकि त्रिज्या अनंत तक जाती है। यह किसी दिए गए त्रिज्या पर अनुपात के अधिकतम से बेहतर सीमा भी है क्योंकि त्रिज्या अनंत तक जाती है। उच्चतम सीमा त्रिज्या पर अधिकतम होने पर भी मौजूद हो सकती है $r$ जैसी कोई सीमा नहीं है $r$ अनंत तक जाता है. उदाहरण के लिए, फ़ंक्शन के लिए

$F(z)=\sum _{n=1}^{\infty }{\frac {z^{10^{n!}}}{(10^{n!})!}}$

का मान है

$(\max _{|z|=r}\log |F(z)|)/r$

पर $r=10^{n!-1}$ का प्रभुत्व है $n-1^{\text{st}}$ शब्द इसलिए हमारे पास स्पर्शोन्मुख अभिव्यक्तियाँ हैं:

${\begin{aligned}\left(\max _{|z|=10^{n!-1}}\log |F(z)|\right)/10^{n!-1}&\sim \left(\log {\frac {(10^{n!-1})^{10^{(n-1)!}}}{(10^{(n-1)!})!}}\right)/10^{n!-1}\\&\sim (\log 10)\left[(n!-1)10^{(n-1)!}-10^{(n-1)!}(n-1)!\right]/10^{n!-1}\\&\sim (\log 10)(n!-1-(n-1)!)/10^{n!-1-(n-1)!}\\\end{aligned}}$

और यह शून्य हो जाता है $n$ अनंत तक जाता है, लेकिन $F(z)$ फिर भी यह घातीय प्रकार 1 का है, जैसा कि बिंदुओं को देखकर देखा जा सकता है $z=10^{n!}$.

सममित उत्तल पिंड के संबंध में घातीय प्रकार

Stein (1957) ने कई जटिल चरों के संपूर्ण कार्यों के लिए घातीय प्रकार का सामान्यीकरण दिया है। कल्पना करना $K$ एक उत्तल समुच्चय, सघन तत्व और सममित उपसमुच्चय है $\mathbb {R} ^{n}$. यह ज्ञात है कि हर ऐसे के लिए $K$ एक संबद्ध मानदंड है (गणित) $\|\cdot \|_{K}$ उस संपत्ति के साथ

$K=\{x\in \mathbb {R} ^{n}:\|x\|_{K}\leq 1\}.$

दूसरे शब्दों में, $K$ में यूनिट बॉल है $\mathbb {R} ^{n}$ इसके संबंध में $\|\cdot \|_{K}$. सेट

$K^{*}=\{y\in \mathbb {R} ^{n}:x\cdot y\leq 1{\text{ for all }}x\in {K}\}$

ध्रुवीय समुच्चय कहा जाता है और यह उत्तल समुच्चय, सघन तत्व और सममित उपसमुच्चय भी है $\mathbb {R} ^{n}$. इसके अलावा, हम लिख सकते हैं

$\|x\|_{K}=\displaystyle \sup _{y\in K^{*}}|x\cdot y|.$

हम विस्तार करते हैं $\|\cdot \|_{K}$ से $\mathbb {R} ^{n}$ को $\mathbb {C} ^{n}$ द्वारा

$\|z\|_{K}=\displaystyle \sup _{y\in K^{*}}|z\cdot y|.$

एक संपूर्ण समारोह $F(z)$ का $n$-सम्मिश्र चर को घातीय प्रकार का कहा जाता है $K$ यदि प्रत्येक के लिए $\varepsilon >0$ वहाँ एक वास्तविक-मूल्यवान स्थिरांक मौजूद है $A_{\varepsilon }$ ऐसा है कि

$|F(z)|<A_{\varepsilon }e^{2\pi (1+\varepsilon )\|z\|_{K}}$

सभी के लिए $z\in \mathbb {C} ^{n}$.

फ्रेचेट स्पेस

घातीय प्रकार के कार्यों का संग्रह $\tau$ मानदंड (गणित) के गणनीय परिवार द्वारा प्रेरित टोपोलॉजिकल स्पेस द्वारा एक पूर्ण अंतरिक्ष समान स्थान, अर्थात् फ़्रेचेट स्पेस, बना सकता है

$\|f\|_{n}=\sup _{z\in \mathbb {C} }\exp \left[-\left(\tau +{\frac {1}{n}}\right)|z|\right]|f(z)|.$

यह भी देखें

• पेली-वीनर प्रमेय
• पेली-वीनर स्थान

संदर्भ

• Stein, E.M. (1957), "Functions of exponential type", Ann. of Math., 2, 65: 582–592, doi:10.2307/1970066, JSTOR 1970066, MR 0085342