अक्षीय झुकाव

From Vigyanwiki
Revision as of 17:31, 25 January 2023 by alpha>Shikhav
"झुकाव" redirects here. For पुस्तक, see झुकाव (पुस्तक).
पृथ्वी का अक्षीय झुकाव (विस्मरण) वर्तमान में लगभग 23.4 ° है और {23.4365472133 ° (2021.1.1) -23.3 ° = .1365472133 ° /[2.40.1846153846107339610733961073961073396107339610733961073396107339610733961073396133333333333333333333333333333333333333333333333333333333333333333336115361153846110136136136136133333333333333333333333 लोगों लोग।2021 =} वर्ष 2760 अगस्त।

खगोल विज्ञान में, अक्षीय झुकाव, जिसे विस्मरण के रूप में भी जाना जाता है, एक निश्चित अक्ष और उसके कक्षीय अक्ष के चारों ओर एक वस्तु के रोटेशन के बीच का कोण है, जो कि इसके कक्षीय विमान (खगोल विज्ञान) के लिए लंबवत रेखा है;समान रूप से, यह इसके भूमध्यरेखीय विमान और कक्षीय विमान के बीच का कोण है।[1] यह कक्षीय झुकाव से भिन्न होता है।

0 डिग्री की विस्मृति में, दो कुल्हाड़ी एक ही दिशा में इंगित करती हैं;यही है, घूर्णी अक्ष कक्षीय विमान के लंबवत है।

उदाहरण के लिए, पृथ्वी की घूर्णी अक्ष, काल्पनिक रेखा है जो उत्तरी ध्रुव और दक्षिण ध्रुव दोनों से होकर गुजरती है, जबकि पृथ्वी की कक्षीय अक्ष काल्पनिक विमान (ज्यामिति) के लिए लंबवत रेखा है, जिसके माध्यम से पृथ्वी के चारों ओर घूमती है।रवि ;पृथ्वी की विशिष्टता या अक्षीय झुकाव इन दो पंक्तियों के बीच का कोण है। पृथ्वी की विस्मरण 22.1 और 24.5 डिग्री के बीच दोलन करती है[2] 41,000 साल के चक्र पर।एक निरंतर अद्यतन सूत्र के आधार पर (यहां लास्कर, 1986, हालांकि 2006 के बाद से IMCCE और IAU P03 मॉडल की सलाह देते हैं), पृथ्वी की औसत विशिष्टता (बिना किसी अव्यवस्था को ध्यान में रखते हुए) वर्तमान में है 23°26′09.8″ (or 23.43605°) और कमी;P03 खगोलीय मॉडल के अनुसार, इसका मूल्य (विस्मरण में पोषण को ध्यान में रखते हुए) 1 जनवरी 2021, 0 tt पर 23 ° 26′11.570 ″ (23.4365472133 °) था।

एक कक्षीय अवधि के दौरान, विस्मरण आमतौर पर काफी नहीं बदलता है, और निश्चित सितारों के खगोलीय क्षेत्र के सापेक्ष अक्षीय समानता ।यह एक पोल को कक्षा के एक तरफ सूर्य की ओर अधिक इंगित किया जाता है, और दूसरी तरफ सूर्य से अधिक दूर - पृथ्वी पर मौसम का कारण।

मानक

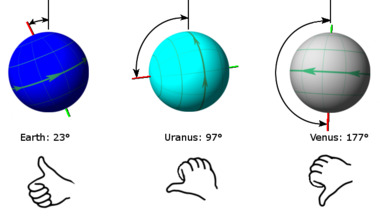
किसी ग्रह के सकारात्मक ध्रुव को दाहिने हाथ के नियम द्वारा परिभाषित किया गया है: यदि दाहिने हाथ की उंगलियों को रोटेशन की दिशा में घुमाया जाता है तो अंगूठा सकारात्मक पोल को इंगित करता है।अक्षीय झुकाव को सकारात्मक ध्रुव की दिशा और कक्षीय विमान के सामान्य के बीच कोण के रूप में परिभाषित किया गया है।पृथ्वी, यूरेनस और वीनस के कोण क्रमशः 23 °, 97 ° और 177 ° हैं।

किसी ग्रह के झुकाव को निर्दिष्ट करने के दो मानक तरीके हैं।एक तरीका ग्रह के उत्तरी ध्रुव पर आधारित है, जिसे पृथ्वी के उत्तरी ध्रुव की दिशा के संबंध में परिभाषित किया गया है, और दूसरा तरीका ग्रह के सकारात्मक पोल पर आधारित है, जो अक्ष-कोण प्रतिनिधित्व द्वारा परिभाषित किया गया है। दाएं हाथ का नियम:

  • अंतर्राष्ट्रीय खगोलीय संघ (IAU) एक ग्रह के उत्तरी ध्रुव को परिभाषित करता है, जो कि सौर मंडल के अविभाज्य विमान के पृथ्वी के उत्तर की ओर स्थित है;[3] इस प्रणाली के तहत, शुक्र 3 ° झुका हुआ है और प्रतिगामी गति को घुमाता है, अधिकांश अन्य ग्रहों के विपरीत।[4][5]
  • IAU एक सकारात्मक पोल को परिभाषित करने के लिए दाहिने हाथ के नियम का भी उपयोग करता है[6] अभिविन्यास का निर्धारण करने के उद्देश्य से।इस सम्मेलन का उपयोग करते हुए, वीनस को 177 ° (उल्टा नीचे) झुकाया जाता है और प्रोग्रेड को घुमाता है।

पृथ्वी

Further information: क्रांतिवृत्त § क्रांतिवृत्त का झुकाव
See also: पृथ्वी का घूर्णन and पृथ्वी-केन्द्रित जड़त्वीय

पृथ्वी की कक्षा को क्रांतिवृत्त विमान के रूप में जाना जाता है, और पृथ्वी#अक्षीय झुकाव और मौसम। पृथ्वी के झुकाव को खगोलविदों के लिए एक्लिप्टिक की विशिष्टता के रूप में जाना जाता है, जो कि खगोलीय क्षेत्र पर एक्लिप्टिक और खगोलीय भूमध्य रेखा के बीच का कोण है।[7] यह ग्रीक अक्षर एप्सिलॉन द्वारा निरूपित किया गया है। ε |

पृथ्वी में वर्तमान में लगभग 23.44 ° का अक्षीय झुकाव है।[8] यह मान अक्षीय पूर्ववर्ती चक्रों में एक स्थिर कक्षीय विमान के सापेक्ष एक ही सापेक्ष है।[9] लेकिन ग्रहण (यानी, पृथ्वी की कक्षा) ग्रहों की गड़बड़ी (खगोल विज्ञान) के कारण चलती है, और एक्लिप्टिक की विशिष्टता एक निश्चित मात्रा नहीं है।वर्तमान में, यह चाप के लगभग दूसरे की दर से घट रहा है। 46.8 ″[10] प्रति शताब्दी (नीचे short शब्द में विवरण देखें)।

इतिहास

भारत और चीन में पृथ्वी की विशिष्टता को यथोचित रूप से सटीक रूप से मापा जा सकता है।[11] प्राचीन यूनानियों में लगभग 350 ईसा पूर्व के बाद से विस्मरण का अच्छा माप था, जब मार्सिले के पायथेस ने गर्मियों के संक्रांति पर एक शंकु की छाया को मापा।[12] लगभग 830 ईस्वी के बारे में, बगदाद के खलीफा अल मामुन ने अपने खगोलविदों को विशिष्टता को मापने के लिए निर्देशित किया, और परिणाम का उपयोग अरब दुनिया में कई वर्षों तक किया गया था।[13] 1437 में, उलुघ बैग ने पृथ्वी के अक्षीय झुकाव को 23 ° 30 ″ 17 ((23.5047 °) के रूप में निर्धारित किया।[14] यह व्यापक रूप से माना जाता था, मध्य युग के दौरान, कि दोनों पूर्ववर्ती और पृथ्वी की विस्मरण एक औसत मूल्य के चारों ओर दोलन किया गया था, 672 वर्षों की अवधि के साथ, एक विचार को विषुवों के trepidation (खगोल विज्ञान) के रूप में जाना जाता है।शायद यह महसूस करने के लिए कि यह गलत था (ऐतिहासिक समय के दौरान) चौदहवीं शताब्दी में Ibn al -shater था[15] और पहले यह महसूस करने के लिए कि 1538 में अपेक्षाकृत स्थिर दर पर विस्मरण कम हो रहा है।[16] पहली सटीक, आधुनिक, पश्चिमी अवलोकन की अवलोकन शायद डेनमार्क से टाइको ब्राहे के थे, लगभग 1584,[17] यद्यपि कई अन्य लोगों द्वारा अवलोकन, जिनमें अल-माहुन, शराफ अल-दीन अल-तसी | अल-तूसी शामिल हैं,[18] जॉर्ज परबाक , रेजिओमोंटेनस और बर्नहार्ड वाल्थर , इसी तरह की जानकारी प्रदान कर सकते थे।

मौसम

Main article: मौसम
पृथ्वी की धुरी पृष्ठभूमि सितारों के संदर्भ में एक ही दिशा में उन्मुख रहती है, चाहे वह अपनी पृथ्वी की कक्षा में हो।उत्तरी गोलार्ध की गर्मी इस आरेख के दाईं ओर होती है, जहां उत्तरी ध्रुव (लाल) को सूर्य की ओर निर्देशित किया जाता है, बाईं ओर सर्दियों में।

पृथ्वी की अक्ष एक वर्ष भर में पृष्ठभूमि सितारों के संदर्भ में एक ही दिशा में झुका हुआ है (चाहे वह अपनी कक्षा में हो)।इसका मतलब यह है कि एक पोल (और पृथ्वी के संबद्ध गोलार्द्धों) को कक्षा के एक तरफ सूर्य से दूर निर्देशित किया जाएगा, और बाद में आधी कक्षा (आधे साल बाद) इस पोल को सूर्य की ओर निर्देशित किया जाएगा।यह पृथ्वी के मौसम का कारण है।उत्तरी गोलार्ध में गर्मी होती है जब उत्तरी ध्रुव सूर्य की ओर निर्देशित होता है।पृथ्वी के अक्षीय झुकाव में भिन्नता मौसम को प्रभावित कर सकती है और संभवतः दीर्घकालिक जलवायु परिवर्तन (सामान्य अवधारणा) में एक कारक है (मिलनकोविच चक्र भी देखें)।

उष्णकटिबंधीय और ध्रुवीय हलकों के लिए पृथ्वी के अक्षीय झुकाव (ε) के बीच संबंध

दोलन

अल्पावधि

लस्कर (1986) से 20,000 वर्षों के लिए एक्लिप्टिक की तिरछीता।रेड पॉइंट वर्ष 2000 का प्रतिनिधित्व करता है।

विस्मृति का सटीक कोणीय मूल्य कई वर्षों में पृथ्वी और ग्रहों की गतियों के अवलोकन से पाया जाता है।खगोलविदों ने नए मौलिक पंचांग का उत्पादन किया क्योंकि अवलोकन खगोल विज्ञान की सटीकता में सुधार होता है और जैसा कि विश्लेषणात्मक गतिशीलता की समझ बढ़ जाती है, और इन पंचांगों से विभिन्न खगोलीय मूल्यों, जिसमें विशिष्टता भी शामिल है, व्युत्पन्न हैं।

वार्षिक पंचांगों को व्युत्पन्न मूल्यों और उपयोग के तरीकों को सूचीबद्ध करते हुए प्रकाशित किया जाता है।1983 तक, किसी भी तारीख के लिए औसत विस्मरण के खगोलीय पंचांग के कोणीय मूल्य की गणना सूर्य के न्यूकॉम्ब के टेबल्स के आधार पर की गई थी, जिन्होंने ग्रहों के पदों का विश्लेषण किया था: लगभग 1895 तक:

ε = 23°27′8.26″ − 46.845″ T − 0.0059″ T2 + 0.00181″ T3

कहाँ पे ε की विशिष्टता है और T एपोच (खगोल विज्ञान) से उष्णकटिबंधीय वर्ष #Besselian वर्ष | B1900.0 प्रश्न में तारीख तक।[19] 1984 से, जेट प्रोपल्शन लेबोरेटरी डेवलपमेंट एफेमेरिस | जेट प्रोपल्शन लेबोरेटरी की डीई सीरीज़ ऑफ कंप्यूटर-जनरेटेड इफेमेराइड्स ने खगोलीय पंचांग के मौलिक पंचांग के रूप में पदभार संभाला।1911 से 1979 तक टिप्पणियों का विश्लेषण करने वाले DE200 पर आधारित तिरछा की गणना की गई:

ε = 23°26′21.448″ − 46.8150″ T − 0.00059″ T2 + 0.001813″ T3

इसके बाद कहाँ T Julian Year (खगोल विज्ञान) epoch (खगोल विज्ञान) #Julian वर्ष और J2000 | J2000.0 से है।[20] जेपीएल के मौलिक पंचांगों को लगातार अपडेट किया गया है।उदाहरण के लिए, P03 खगोलीय मॉडल के पक्ष में 2006 में IAU संकल्प के अनुसार, 2010 के लिए खगोलीय पंचांग निर्दिष्ट करता है:[21]

ε = 23°26′21.406″ − 46.836769″ T − 0.0001831″ T2 + 0.00200340″ T3 − 5.76″ × 10−7 T4 − 4.34″ × 10−8 T5

विस्मरण के लिए ये भाव अपेक्षाकृत कम समय अवधि में उच्च परिशुद्धता के लिए अभिप्रेत हैं, शायद ± कई शताब्दियों।[22] जे। लास्कर ने ऑर्डर करने के लिए एक अभिव्यक्ति की गणना की T10 1000 वर्षों में 0.02 ″ से अच्छा और 10,000 वर्षों में कई मिनट चाप।

ε = 23°26′21.448″ − 4680.93″ t − 1.55″ t2 + 1999.25″ t3 − 51.38″ t4 − 249.67″ t5 − 39.05″ t6 + 7.12″ t7 + 27.87″ t8 + 5.79″ t9 + 2.45″ t10

यहां कहां t एपोच (खगोल विज्ञान)#जूलियन वर्ष और J2000 | J2000.0 से 10,000 जूलियन डे का गुणक है।[23] ये अभिव्यक्तियाँ तथाकथित माध्य वस्तु के लिए हैं, अर्थात्, अल्पकालिक विविधताओं से मुक्त विस्मरण।चंद्रमा और पृथ्वी की आवधिक गतियों में इसकी कक्षा में बहुत छोटी (9.2 मिनट चाप) की छोटी अवधि (लगभग 18.6 वर्ष) पृथ्वी के रोटेशन अक्ष के दोलनों का कारण बनता है, जिसे खगोलीय पोषण के रूप में जाना जाता है, जो पृथ्वी की विषमता के लिए एक आवधिक घटक को जोड़ता है।[24][25] सही या तात्कालिक विस्मरण में यह पोषण शामिल है।[26]


दीर्घकालिक

Main article: सौर मंडल का गठन और विकास
Main article: मिलनकोविच चक्र

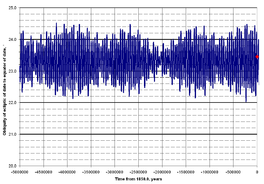
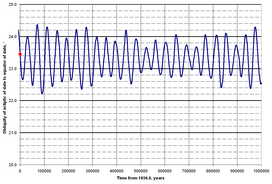
सौर प्रणाली के व्यवहार को अनुकरण करने के लिए संख्यात्मक तरीकों का उपयोग करना, पृथ्वी की कक्षा में दीर्घकालिक परिवर्तन, और इसलिए इसकी विशिष्टता, कई मिलियन वर्षों की अवधि में जांच की गई है।पिछले 5 मिलियन वर्षों के लिए, पृथ्वी की विशिष्टता के बीच भिन्नता है 22°2′33″ और 24°30′16″, 41,040 वर्षों की औसत अवधि के साथ।यह चक्र पूर्ववर्ती का एक संयोजन है और ecliptic की गति में सबसे बड़ा जोड़ है।अगले 1 मिलियन वर्षों के लिए, चक्र के बीच की विस्मृति को आगे बढ़ाएगा 22°13′44″ और 24°20′50″.[27] चंद्रमा का पृथ्वी की तिरछीता पर एक स्थिर प्रभाव है।1993 में किए गए आवृत्ति मानचित्र विश्लेषण ने सुझाव दिया कि, चंद्रमा की अनुपस्थिति में, ऑर्बिटल प्रतिध्वनि और सौर मंडल की स्थिरता के कारण विस्मरण तेजी से बदल सकता है, कुछ मिलियन वर्षों में 90 ° तक पहुंचने के लिए (ऑर्बिट भी देखेंचाँद की)।[28][29] हालांकि, अधिक हाल के संख्यात्मक सिमुलेशन[30] 2011 में निर्मित ने संकेत दिया कि यहां तक कि चंद्रमा की अनुपस्थिति में, पृथ्वी की विस्मरण काफी अस्थिर नहीं हो सकती है;केवल लगभग 20-25 ° से भिन्न।इस विरोधाभास को हल करने के लिए, विस्मरण दर की कमी की गणना की गई है, और यह पाया गया कि पृथ्वी की विस्मरण में 90 ° तक पहुंचने में अरबों से अधिक वर्षों का समय लगता है।[31] चंद्रमा का स्थिर प्रभाव 2 & nbsp; अरब वर्ष से कम के लिए जारी रहेगा।चूंकि चंद्रमा ज्वारीय त्वरण के कारण पृथ्वी से पुनरावृत्ति करता रहता है, इसलिए प्रतिध्वनि हो सकती है जो कि विस्मरण के बड़े दोलनों का कारण बनेगी।[32]

Long-term obliquity of the ecliptic. Left: for the past 5 million years; note that the obliquity varies only from about 22.0° to 24.5°. Right: for the next 1 million years; note the approx. 41,000-year period of variation. In both graphs, the red point represents the year 1850. (Source: Berger, 1976).


सौर मंडल निकाय

Comparison of the rotation period (sped up 10 000 times, negative values denoting retrograde), flattening and axial tilt of the planets and the Moon (SVG animation)

सौर मंडल के सभी चार, चट्टानी ग्रहों के सभी चार अतीत में उनकी विशिष्टता के बड़े बदलाव हो सकते हैं।चूंकि विस्मरण रोटेशन की धुरी और कक्षीय विमान के लंबवत दिशा के बीच का कोण है, इसलिए यह अन्य ग्रहों के प्रभाव के कारण कक्षीय विमान में परिवर्तन के रूप में बदल जाता है।लेकिन रोटेशन की धुरी एक ग्रह के भूमध्यरेखीय उभार पर सूर्य द्वारा फेंकने वाले टॉर्क के कारण (अक्षीय पूर्ववर्ती) भी स्थानांतरित हो सकती है।पृथ्वी की तरह, सभी चट्टानी ग्रह अक्षीय पूर्वता दिखाते हैं।यदि पूर्ववर्ती दर बहुत तेज़ होती तो तिरछापन वास्तव में काफी स्थिर रहेगा क्योंकि कक्षीय विमान में परिवर्तन होता है।[33] अन्य चीजों के बीच ज्वारीय त्वरण और ग्रहीय कोर -मेंटल (भूविज्ञान) बातचीत के कारण दर भिन्न होती है।जब किसी ग्रह की पूर्ववर्ती दर कुछ मूल्यों तक पहुंचती है, तो कक्षीय प्रतिध्वनि अवलोकन में बड़े बदलाव का कारण बन सकती है।गुंजयमान दरों में से एक होने वाले योगदान का आयाम गुंजयमान दर और पूर्ववर्ती दर के बीच के अंतर से विभाजित होता है, इसलिए जब दोनों समान होते हैं तो यह बड़ा हो जाता है।[33]

बुध (ग्रह) और शुक्र को सूर्य के ज्वार के विघटन द्वारा सबसे अधिक संभावना है।पृथ्वी को चंद्रमा द्वारा स्थिर किया गया था, जैसा कि ऊपर उल्लेख किया गया था, लेकिन इसके चंद्रमा#गठन से पहले, पृथ्वी भी, अस्थिरता के समय से गुजर सकती थी।मंगल की विशिष्टता लाखों वर्षों में काफी परिवर्तनशील है और अराजक अवस्था में हो सकती है;यह कुछ लाखों वर्षों में 0 ° से 60 ° तक भिन्न होता है, जो ग्रहों के गड़बड़ी (खगोल विज्ञान) पर निर्भर करता है।[28][34] कुछ लेखक इस बात पर विवाद करते हैं कि मंगल की विस्मरण अराजक है, और दिखाती है कि ज्वार का अपव्यय और चिपचिपा कोर-मेंटल युग्मन इसके लिए पर्याप्त है, जो पारा और शुक्र के समान पूरी तरह से नम स्थिति तक पहुंच गया है।[4][35] मंगल के अक्षीय झुकाव में सामयिक बदलावों को मंगल के अस्तित्व के दौरान नदियों और झीलों की उपस्थिति और गायब होने के लिए एक स्पष्टीकरण के रूप में सुझाया गया है।एक बदलाव से वातावरण में मीथेन का फटने का कारण बन सकता है, जिससे गर्म हो जाता है, लेकिन फिर मीथेन नष्ट हो जाएगा और जलवायु फिर से आ जाएगी।[36][37] बाहरी ग्रहों के तिरछे को अपेक्षाकृत स्थिर माना जाता है।

Axis and rotation of selected Solar System bodies
Body NASA, J2000.0[38] epoch IAU, 0h 0 January 2010 TT[39] epoch
Axial tilt
(degrees) 		North Pole Rotational
period
(hours) 		Axial tilt
(degrees) 		North Pole Rotation
(deg./day)
R.A. (degrees) Dec. (degrees) R.A. (degrees) Dec. (degrees)
Sun 7.25 286.13 63.87 609.12[upper-alpha 1] 7.25[upper-alpha 2] 286.15 63.89 14.18
Mercury 0.03 281.01 61.41 1407.6 0.01 281.01 61.45 6.14
Venus 2.64 272.76 67.16 −5832.6 2.64 272.76 67.16 −1.48
Earth 23.44 0.00 90.00 23.93 23.44 Undefined 90.00 360.99
Moon 6.68 – – 655.73 1.54[upper-alpha 3] 270.00 66.54 13.18
Mars 25.19 317.68 52.89 24.62 25.19 317.67 52.88 350.89
Jupiter 3.13 268.06 64.50 9.93[upper-alpha 4] 3.12 268.06 64.50 870.54[upper-alpha 4]
Saturn 26.73 40.59 83.54 10.66[upper-alpha 4] 26.73 40.59 83.54 810.79[upper-alpha 4]
Uranus 82.23 257.31 −15.18 −17.24[upper-alpha 4] 82.23 257.31 −15.18 −501.16[upper-alpha 4]
Neptune 28.32 299.33 42.95 16.11[upper-alpha 4] 28.33 299.40 42.95 536.31[upper-alpha 4]
Pluto[upper-alpha 5] 57.47 312.99[upper-alpha 5] 6.16[upper-alpha 5] −153.29 60.41 312.99 6.16 −56.36
  1. ↑ At 16° latitude; the Sun's rotation varies with latitude.
  2. ↑ With respect to the ecliptic of 1850.
  3. ↑ With respect to the ecliptic; the Moon's orbit is inclined 5.16° to the ecliptic.
  4. ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 From the origin of the radio emissions; the visible clouds generally rotate at different rate.
  5. ↑ 5.0 5.1 5.2 NASA lists the coordinates of Pluto's positive pole; noted values have been reinterpreted to correspond to the north/negative pole.


एक्स्ट्रासोलर ग्रह

तारकीय वस्तु ψs, यानी अपने ग्रहों में से एक के कक्षीय विमान के संबंध में एक तारे का अक्षीय झुकाव, केवल कुछ प्रणालियों के लिए निर्धारित किया गया है।लेकिन 2012 तक 49 सितारों के लिए, स्काई-प्रोजेक्टेड स्पिन-ऑर्बिट मिसलिग्न्मेंट λ देखा गया है,[40] जो एक निचली सीमा के रूप में कार्य करता है ψs।इनमें से अधिकांश माप रॉसिटर -मैक्लॉघलिन प्रभाव पर भरोसा करते हैं।अब तक, एक एक्स्ट्रासोलर ग्रह की विशिष्टता को बाधित करना संभव नहीं है।लेकिन ग्रह के घूर्णी चपटा और चंद्रमाओं और/या छल्ले के प्रवेश, जो उच्च-सटीक फोटोमेट्री के साथ ट्रेस करने योग्य हैं, उदा।स्पेस-आधारित केप्लर स्पेस टेलीस्कोप द्वारा, तक पहुंच प्रदान कर सकता है ψp[clarification needed] निकट भविष्य में।

एस्ट्रोफिजिसिस्ट ने एक्स्ट्रासोलर ग्रह ों की विशिष्टता की भविष्यवाणी करने के लिए ज्वारीय सिद्धांतों को लागू किया है।यह दिखाया गया है कि कम-द्रव्यमान सितारों के आसपास रहने योग्य क्षेत्र में एक्सोप्लैनेट्स की विस्मरण 10 से कम में मिट जाती है9 वर्ष,[41][42] जिसका अर्थ है कि उनके पास मौसम नहीं होगा[clarification needed] जैसा कि पृथ्वी है।

यह भी देखें

संदर्भ

  1. ↑ U.S. Naval Observatory Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books. p. 733. ISBN 978-0-935702-68-2.
  2. ↑ "Earth Is tilted". timeanddate.com. Retrieved 25 August 2017.
  3. ↑ Explanatory Supplement 1992, p. 384
  4. ↑ 4.0 4.1 Correia, Alexandre C. M.; Laskar, Jacques; de Surgy, Olivier Néron (May 2003). "Long-term evolution of the spin of Venus I. theory" (PDF). Icarus. 163 (1): 1–23. Bibcode:2003Icar..163....1C. doi:10.1016/S0019-1035(03)00042-3. Archived (PDF) from the original on 9 October 2022.
  5. ↑ Correia, A. C. M.; Laskar, J. (2003). "Long-term evolution of the spin of Venus: II. numerical simulations" (PDF). Icarus. 163 (1): 24–45. Bibcode:2003Icar..163...24C. doi:10.1016/S0019-1035(03)00043-5. Archived (PDF) from the original on 9 October 2022.
  6. ↑ Seidelmann, P. Kenneth; Archinal, B. A.; a'Hearn, M. F.; Conrad, A.; Consolmagno, G. J.; Hestroffer, D.; Hilton, J. L.; Krasinsky, G. A.; Neumann, G.; Oberst, J.; Stooke, P.; Tedesco, E. F.; Tholen, D. J.; Thomas, P. C.; Williams, I. P. (2007). "Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006". Celestial Mechanics and Dynamical Astronomy. 98 (3): 155–180. Bibcode:2007CeMDA..98..155S. doi:10.1007/s10569-007-9072-y.
  7. ↑ U.S. Naval Observatory Nautical Almanac Office; U.K. Hydrographic Office; H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. US Government Printing Office. p. M11. ISBN 978-0-7077-4082-9.
  8. ↑ "Glossary" in Astronomical Almanac Online. (2018). Washington DC: United States Naval Observatory. s.v. obliquity.
  9. ↑ Chauvenet, William (1906). A Manual of Spherical and Practical Astronomy. Vol. 1. J. B. Lippincott. pp. 604–605.
  10. ↑ Ray, Richard D.; Erofeeva, Svetlana Y. (4 February 2014). "Long‐period tidal variations in the length of day". Journal of Geophysical Research: Solid Earth. 119 (2): 1498–1509. Bibcode:2014JGRB..119.1498R. doi:10.1002/2013JB010830.
  11. ↑ Wittmann, A. (1979). "The Obliquity of the Ecliptic". Astronomy and Astrophysics. 73 (1–2): 129–131. Bibcode:1979A&A....73..129W.
  12. ↑ Gore, J. E. (1907). Astronomical Essays Historical and Descriptive. Chatto & Windus. p. 61.
  13. ↑ Marmery, J. V. (1895). Progress of Science. Chapman and Hall, ld. p. 33.
  14. ↑ Sédillot, L.P.E.A. (1853). Prolégomènes des tables astronomiques d'OlougBeg: Traduction et commentaire. Paris: Firmin Didot Frères. pp. 87 & 253.
  15. ↑ Saliba, George (1994). A History of Arabic Astronomy: Planetary Theories During the Golden Age of Islam. p. 235.
  16. ↑ Dreyer, J. L. E. (1890). Tycho Brahe. A. & C. Black. p. 355.
  17. ↑ Dreyer (1890), p. 123
  18. ↑ Sayili, Aydin (1981). The Observatory in Islam. p. 78.
  19. ↑ U.S. Naval Observatory Nautical Almanac Office; H.M. Nautical Almanac Office (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office. Section 2B.
  20. ↑ U.S. Naval Observatory; H.M. Nautical Almanac Office (1989). The Astronomical Almanac for the Year 1990. US Government Printing Office. p. B18. ISBN 978-0-11-886934-8.
  21. ↑ Astronomical Almanac 2010, p. B52
  22. ↑ Newcomb, Simon (1906). A Compendium of Spherical Astronomy. MacMillan. pp. 226–227.
  23. ↑ See table 8 and eq. 35 in Laskar, J. (1986). "Secular terms of classical planetary theories using the results of general theory". Astronomy and Astrophysics. 157 (1): 59–70. Bibcode:1986A&A...157...59L. and erratum to article Laskar, J. (1986). "Erratum: Secular terms of classical planetary theories using the results of general theory". Astronomy and Astrophysics. 164: 437. Bibcode:1986A&A...164..437L. Units in article are arcseconds, which may be more convenient.
  24. ↑ Explanatory Supplement (1961), sec. 2C
  25. ↑ "Basics of Space Flight, Chapter 2". Jet Propulsion Laboratory/NASA. 29 October 2013. Retrieved 26 March 2015.
  26. ↑ Meeus, Jean (1991). "Chapter 21". Astronomical Algorithms. Willmann-Bell. ISBN 978-0-943396-35-4.
  27. ↑ Berger, A.L. (1976). "Obliquity and Precession for the Last 5000000 Years". Astronomy and Astrophysics. 51 (1): 127–135. Bibcode:1976A&A....51..127B.
  28. ↑ 28.0 28.1 Laskar, J.; Robutel, P. (1993). "The Chaotic Obliquity of the Planets" (PDF). Nature. 361 (6413): 608–612. Bibcode:1993Natur.361..608L. doi:10.1038/361608a0. S2CID 4372237. Archived from the original (PDF) on 23 November 2012.
  29. ↑ Laskar, J.; Joutel, F.; Robutel, P. (1993). "Stabilization of the Earth's Obliquity by the Moon" (PDF). Nature. 361 (6413): 615–617. Bibcode:1993Natur.361..615L. doi:10.1038/361615a0. S2CID 4233758. Archived (PDF) from the original on 9 October 2022.
  30. ↑ Lissauer, J.J.; Barnes, J.W.; Chambers, J.E. (2011). "Obliquity variations of a moonless Earth" (PDF). Icarus. 217 (1): 77–87. Bibcode:2012Icar..217...77L. doi:10.1016/j.icarus.2011.10.013. Archived (PDF) from the original on 8 June 2013.
  31. ↑ Li, Gongjie; Batygin, Konstantin (20 July 2014). "On the Spin-axis Dynamics of a Moonless Earth". Astrophysical Journal. 790 (1): 69–76. arXiv:1404.7505. Bibcode:2014ApJ...790...69L. doi:10.1088/0004-637X/790/1/69. S2CID 119295403.
  32. ↑ Ward, W.R. (1982). "Comments on the Long-Term Stability of the Earth's Obliquity". Icarus. 50 (2–3): 444–448. Bibcode:1982Icar...50..444W. doi:10.1016/0019-1035(82)90134-8.
  33. ↑ 33.0 33.1 William Ward (20 July 1973). "Large-Scale Variations in the Obliquity of Mars". Science. 181 (4096): 260–262. Bibcode:1973Sci...181..260W. doi:10.1126/science.181.4096.260. PMID 17730940. S2CID 41231503.
  34. ↑ Touma, J.; Wisdom, J. (1993). "The Chaotic Obliquity of Mars" (PDF). Science. 259 (5099): 1294–1297. Bibcode:1993Sci...259.1294T. doi:10.1126/science.259.5099.1294. PMID 17732249. S2CID 42933021. Archived (PDF) from the original on 25 June 2010.
  35. ↑ Correia, Alexandre C.M; Laskar, Jacques (2009). "Mercury's capture into the 3/2 spin-orbit resonance including the effect of core-mantle friction". Icarus. 201 (1): 1–11. arXiv:0901.1843. Bibcode:2009Icar..201....1C. doi:10.1016/j.icarus.2008.12.034. S2CID 14778204.
  36. ↑ Rebecca Boyle (7 October 2017). "Methane burps on young Mars helped it keep its liquid water". New Scientist.
  37. ↑ Edwin Kite; et al. (2 October 2017). "Methane bursts as a trigger for intermittent lake-forming climates on post-Noachian Mars" (PDF). Nature Geoscience. 10 (10): 737–740. arXiv:1611.01717. Bibcode:2017NatGe..10..737K. doi:10.1038/ngeo3033. S2CID 102484593. Archived (PDF) from the original on 23 July 2018.
  38. ↑ Planetary Fact Sheets, at http://nssdc.gsfc.nasa.gov
  39. ↑ Astronomical Almanac 2010, pp. B52, C3, D2, E3, E55
  40. ↑ Heller, R. "Holt-Rossiter-McLaughlin Encyclopaedia". René Heller. Retrieved 24 February 2012.
  41. ↑ Heller, R.; Leconte, J.; Barnes, R. (2011). "संभावित रहने योग्य ग्रहों के ज्वारीय अवलोकन विकास". Astronomy and Astrophysics. 528: A27. arXiv:1101.2156. Bibcode:2011A&A...528A..27H. doi:10.1051/0004-6361/201015809. S2CID 118784209.
  42. ↑ Heller, R.; Leconte, J.; Barnes, R. (2011). "एक्स्ट्रासोलर ग्रहों और ज्वारीय स्पिन विकास की आदत". Origins of Life and Evolution of Biospheres. 41 (6): 539–43. arXiv:1108.4347. Bibcode:2011OLEB...41..539H. doi:10.1007/s11084-011-9252-3. PMID 22139513. S2CID 10154158.


बाहरी कड़ियाँ

Template:Astronomy in medieval Islam

Template:Climate oscillations

Retrieved from ‘https://www.vigyanwiki.in/index.php?title=अक्षीय_झुकाव&oldid=72591’