वास्तविक प्रक्षेपी तल

The fundamental polygon of the projective plane.

The Möbius strip with a single edge, can be closed into a projective plane by gluing opposite open edges together.

In comparison, the Klein bottle is a Möbius strip closed into a cylinder.

गणित में, वास्तविक प्रक्षेपी तल एक सघन गैर-उन्मुखता द्वि-आयामी विविध का एक उदाहरण है; दूसरे शब्दों में, एक पक्षीय सतह (टोपोलॉजी) है। यह स्वयं अन्तर्विभाजक किए बिना मानक त्रि-आयामी स्थान में अंतर्निहित नहीं किया जा सकता है। इसमें ज्यामिति के लिए मूलभूत अनुप्रयोग हैं, क्योंकि वास्तविक प्रक्षेपी तल का सामान्य निर्माण मूल के माध्यम से गुजरने वाली $\mathbb {R} ^{3}$ रेखा के स्थान के रूप में है।

मोबियस पट्टी के आधार पर एक निर्माण के संदर्भ में, तल को प्रायः स्थलीय रूप से वर्णित किया जाता है: यदि कोई मोबियस पट्टी के (एकल) किनारे को सही दिशा में चिपका सकता है, तो वह प्रक्षेपी तल प्राप्त करेगा। (यह त्रि-आयामी स्थान में सतह के स्वयं को प्रतिच्छेद किए बिना नहीं किया जा सकता है।) समान रूप से, मोबियस पट्टी की सीमा के साथ एक डिस्क को चिपकाने से प्रक्षेपी तल मिलता है। टोपोलॉजिकल रूप से, इसमें यूलर की विशेषता 1 है, इसलिए 1 का एक जीनस (गणित) (गैर-उन्मुख जीनस, यूलर जीनस) है।

चूंकि मोबियस पट्टी, के स्थान पर , एक वर्ग (ज्यामिति) से इसके दो पक्षों को एक साथ आधे-मोड़ के साथ जोड़कर बनाया जा सकता है, वास्तविक प्रक्षेपी तल को एक इकाई वर्ग के रूप में दर्शाया जा सकता है (अर्थात, [0, 1] × [0,1]) निम्नलिखित तुल्यता संबंधों द्वारा पहचाने गए पक्षों के साथ:

(0, y) ~ (1, 1 − y) के लिए 0 ≤ y ≤ 1

और

(x, 0) ~ (1 − x, 1) के लिए 0 ≤ x ≤ 1,

जैसा कि यहां दिखाए गए सबसे बाएं आरेख में है।

उदाहरण

प्रक्षेपी ज्यामिति आवश्यक रूप से वक्रता से संबंधित नहीं है और वास्तविक प्रक्षेपी तल को कई अलग-अलग विधियों से यूक्लिडियन तल या 3-स्थान में घुमाया और रखा जा सकता है। कुछ अधिक महत्वपूर्ण उदाहरणों का वर्णन नीचे किया गया है।

प्रक्षेपी तल को त्रि-आयामी यूक्लिडियन स्थान में अंतर्निहित नहीं किया जा सकता है (जो बिना प्रतिच्छेदन के है)। प्रमाण है कि प्रक्षेपी तल त्रि-आयामी यूक्लिडियन स्थान में अंतर्निहित नहीं होता है: यह मानते हुए कि यह अंतर्निहित करता है, यह जॉर्डन वक्र प्रमेय द्वारा त्रि-आयामी यूक्लिडियन स्थान में एक सघन क्षेत्र को बाध्य करेगा। बाह्य-संकेत इकाई सामान्य सदिश क्षेत्र तब परिसीमा विविध का अभिविन्यसनीय (गणित) देगा, परन्तु परिसीमा विविध प्रक्षेपी तल होगा, जो अभिविन्यसनीय नहीं है। यह एक विरोधाभास है, और इसलिए हमारी यह धारणा है कि यह अंतर्निहित करता है, असत्य होना चाहिए।

प्रक्षेप्य क्षेत्र

एक गोले पर विचार करें, और गोले के बड़े वृत्तों को रेखाएँ होने दें, और प्रतिव्यासांत बिंदुओं के युग्मों को बिंदु होने दें। यह जाँचना आसान है कि यह प्रणाली प्रक्षेपी तल के लिए आवश्यक स्वयंसिद्धों का पालन करती है:

• विभिन्न बड़े वृत्तों की कोई भी युग्म प्रतिलोम-संबंधी बिंदुओं के एक युग्म पर मिलती है; और
• प्रतिलोम-संबंधी बिंदुओं के कोई भी दो अलग-अलग युग्म एक बड़े वृत्त पर स्थित होते हैं।

यदि हम गोले के प्रत्येक बिंदु को उसके प्रतिमुख बिंदु से पहचानते हैं, तो हमें वास्तविक प्रक्षेपी तल का प्रतिनिधित्व मिलता है जिसमें प्रक्षेपी तल के बिंदु सत्यतः बिंदु होते हैं। इसका अर्थ यह है कि प्रक्षेपी तल, गोले को समतुल्यता संबंध ~ के अंतर्गत तुल्यता वर्गों में विभाजित करके प्राप्त किए गए गोले का भागफल स्थान है, जहाँ x ~ y यदि y = x या y = −x है। गोले का यह भागफल स्थान R³ में मूल से गुजरने वाली सभी रेखाओं के संग्रह के साथ समरूप है।

क्षेत्र से वास्तविक प्रक्षेपी तल पर भागफल प्रतिचित्र सत्यतः एक दो शीट (अर्थात दो-से-एक) आवरण प्रतिचित्र है। यह इस प्रकार है कि वास्तविक प्रक्षेपी तल का मौलिक समूह क्रम 2 का चक्रीय समूह है; अर्थात, पूर्णांक सापेक्ष 2। उत्पादक होने के लिए ऊपर की आकृति से लूप AB ले सकते हैं।

प्रक्षेप्य गोलार्द्ध

भूमध्य रेखा पर एक साथ विपरीत बिंदुओं को जोड़कर एक गोलार्द्ध एक वास्तविक प्रक्षेप्य तल का प्रतिनिधित्व कर सकता है।

क्योंकि गोला वास्तविक प्रक्षेपी तल को दो बार ढकता है, समतल को एक बंद गोलार्द्ध के रूप में दर्शाया जा सकता है जिसके किनारे के चारों ओर विपरीत बिंदु समान रूप से पहचाने जाते हैं।

लड़के की सतह - एक निमज्जन

प्रक्षेपी तल 3-स्थान में निमज्जन (गणित) हो सकता है (स्रोत स्थान के स्थानीय निकटवर्ती में आत्म-प्रतिच्छेदन नहीं हैं)। लड़के की सतह निमज्जन का एक उदाहरण है।

बहुफलकीय उदाहरणों में कम से कम नौ फलक होने चाहिए।

रोमन सतह

रोमन सतह का एक एनीमेशन

स्टेनर की रोमन सतह 3-स्थान में प्रक्षेपी तल का एक अधिक अपभ्रष्ट प्रतिचित्र है, जिसमें एक संकर-कैप है।

टेट्राहेमीहेक्साइड्रोन वास्तविक प्रक्षेपी तल का बहुफलकीय प्रतिनिधित्व है।

एक बहुतल प्रतिनिधित्व टेट्राहेमीहेक्साइड्रोन है, जिसका वही सामान्य रूप है जो स्टेनर की रोमन सतह जैसा है, यहाँ दिखाया गया है।

अर्ध बहुकोणीय आकृति

विपरीत दिशा में देखते हुए, कुछ अमूर्त नियमित बहुतलीय - अर्धघन (ज्यामिति) , अर्ध-द्वादशफलक, और अर्ध-विंशतिफलक - प्रक्षेपी तल में नियमित आंकड़े के रूप में बनाए जा सकते हैं; प्रक्षेपी बहुकोणीय आकृति भी देखें।

समतलीय प्रक्षेप

प्रक्षेपी तल के विभिन्न प्लानर (फ्लैट) प्रक्षेपों या प्रतिचित्रों का वर्णन किया गया है। 1874 में क्लेन ने प्रतिचित्रण का वर्णन किया:: $k(x,y)=\left(1+x^{2}+y^{2}\right)^{\frac {1}{2}}{\begin{pmatrix}x\\y\end{pmatrix}}$

प्रक्षेपी गोलार्द्ध का एक तल पर केंद्रीय प्रक्षेपण नीचे वर्णित सामान्य अनंत प्रक्षेपी तल उत्पन्न करता है।

संकर-कैप्ड डिस्क

एक डिस्क (गणित) को संकर-कैप से चिपकाकर एक बंद सतह प्राप्त की जाती है। इस सतह को निम्नलिखित समीकरणों द्वारा प्राचलिक रूप से दर्शाया जा सकता है:

${\begin{aligned}X(u,v)&=r\,(1+\cos v)\,\cos u,\\Y(u,v)&=r\,(1+\cos v)\,\sin u,\\Z(u,v)&=-\operatorname {tanh} \left(u-\pi \right)\,r\,\sin v,\end{aligned}}$

जहाँ u और v दोनों का परिसर 0 से 2π तक है।

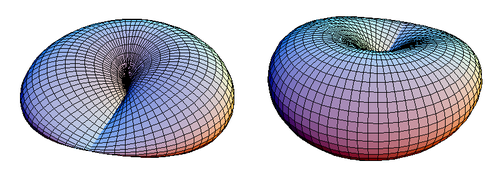
ये समीकरण एक टोरस्र्स के समान हैं। चित्र 1 एक बंद संकर-कैप्ड डिस्क दिखाता है।

चित्र 1. क्रॉस-कैप्ड डिस्क के दो दृश्य।

एक संकर-कैप्ड डिस्क में समरूपता का एक तल होता है जो दोहरे बिंदुओं के रेखा खंड से होकर गुजरता है। चित्र 1 में संकर-कैप्ड डिस्क को सममिति z = 0 के तल के ऊपर से देखा जा सकता है, परन्तु नीचे से देखने पर यह वैसी ही दिखेगी।

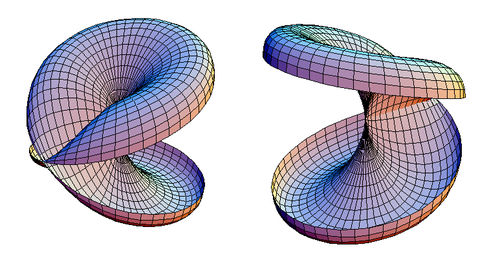
एक संकर-कैप्ड डिस्क को इसके समरूपता के तल के साथ खुला काटा जा सकता है, जबकि यह सुनिश्चित किया जाता है कि इसके किसी भी दोहरे बिंदु के साथ कटौती न हो। परिणाम चित्र 2 में दिखाया गया है।

चित्र 2. एक क्रॉस-कैप्ड डिस्क के दो दृश्य जो खुले में कटा हुआ है।

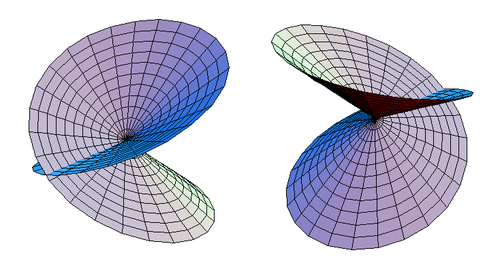
एक बार यह अपवाद हो जाने के बाद, यह देखा जाएगा कि कटा हुआ संकर-कैप्ड डिस्क स्व-प्रतिच्छेदी डिस्क के लिए समरूप है, जैसा कि चित्र 3 में दिखाया गया है।

चित्र 3. एक स्व-प्रतिच्छेदी डिस्क के दो वैकल्पिक दृश्य।

स्व-प्रतिच्छेदी डिस्क एक साधारण डिस्क के लिए समरूप है। स्व-प्रतिच्छेदी डिस्क के प्राचलिक समीकरण हैं:

${\begin{aligned}X(u,v)&=r\,v\,\cos 2u,\\Y(u,v)&=r\,v\,\sin 2u,\\Z(u,v)&=r\,v\,\cos u,\end{aligned}}$

जहाँ u 0 से 2π तक और v 0 से 1 तक होता है।

स्व-प्रतिच्छेदी डिस्क को समरूपता के तल पर प्रक्षेपित करना (पहले दिए गए प्राचलिक में z = 0) जो मात्र दोहरे बिंदुओं से होकर गुजरता है, परिणाम एक साधारण डिस्क है जो स्वयं को दोहराती है (स्वयं पर दोगुनी हो जाती है)।

समतल z = 0 स्व-प्रतिच्छेदी डिस्क को डिस्क की एक युग्म में काटता है जो एक दूसरे के दर्पण प्रतिबिंब (गणित) हैं। डिस्क के केंद्र उत्पत्ति (गणित) पर होते हैं।

अब डिस्क के किनारों पर विचार करें (v = 1 के साथ)। स्व-प्रतिच्छेदी डिस्क के किनारे पर बिंदु युग्मों में आते हैं जो समतल z = 0 के संबंध में एक दूसरे के प्रतिबिंब होते हैं।

बिंदुओं के इन युग्मों की पहचान करके, उन्हें एक दूसरे के समतुल्य बनाकर एक संकर-कैप्ड डिस्क बनाई जाती है। इसका तात्पर्य है कि मापदंडों (u, 1) और निर्देशांक $(r\,\cos 2u,r\,\sin 2u,r\,\cos u)$ के साथ एक बिंदु बिंदु (u + π, 1) से पहचाना जाता है जिसका निर्देशांक $(r\,\cos 2u,r\,\sin 2u,-r\,\cos u)$ है। परन्तु इसका तात्पर्य यह है कि (समतुल्य) साधारण डिस्क के किनारे पर विपरीत बिंदुओं के युग्मों एक दूसरे के साथ पहचाने जाते हैं; डिस्क से वास्तविक प्रक्षेपी तल इस प्रकार बनता है। इसलिए, चित्र 1 में दिखाई गई सतह (डिस्क के साथ संकर-कैप) स्थैतिक रूप से वास्तविक प्रक्षेपी तल RP^{2 के समतुल्य है।}

सजातीय निर्देशांक

Main article: सजातीय निर्देशांक

समतल में बिंदुओं को सजातीय निर्देशांक द्वारा दर्शाया जा सकता है। एक बिंदु में सजातीय निर्देशांक [x : y : z] होते हैं, जहां निर्देशांक [x : y : z] और [tx : ty : tz] को t के सभी अशून्य मानों के लिए एक ही बिंदु का प्रतिनिधित्व करने के लिए माना जाता है। निर्देशांक [x : y : 1] वाले बिंदु सामान्य वास्तविक तल होते हैं, जिन्हें प्रक्षेपी तल का 'परिमित भाग' कहा जाता है, और निर्देशांक [x : y : 0] वाले बिंदु, जिन्हें 'अनंत' या 'आदर्श बिंदु' कहा जाता है , एक रेखा बनाते हैं जिसे कहा जाता है अनंत पर रेखा। (सजातीय निर्देशांक [0 : 0 : 0] किसी भी बिंदु का प्रतिनिधित्व नहीं करते हैं।)

समतल में रेखाओं को सजातीय निर्देशांक द्वारा भी दर्शाया जा सकता है। R³ में समतल ax + by + cz = 0 के अनुरूप एक प्रक्षेपी रेखा में सजातीय निर्देशांक (a : b : c) हैं। इस प्रकार, इन निर्देशांकों में d के सभी शून्येतर मानों के लिए तुल्यता संबंध (a : b : c) = (da : db : dc) है। इसलिए एक ही रेखा का एक अलग समीकरण dax+dby+dcz=0 समान सजातीय निर्देशांक देता है। एक बिंदु [x : y : z] एक रेखा (a : b : c) पर स्थित है यदि ax + by +cz = 0 है। इसलिए, निर्देशांक (a : b : c) वाली रेखाएँ जहाँ a, b दोनों 0 नहीं हैं, सामान्य वास्तविक तल की रेखाओं के अनुरूप हैं, क्योंकि उनमें ऐसे बिंदु हैं जो अनंत पर नहीं हैं। निर्देशांक (0 : 0 : 1) वाली रेखा अनंत पर रेखा है, क्योंकि इस पर मात्र वही बिंदु हैं जिनके समीप z = 0 है।

अंक, रेखाएँ और तल

P² में एक रेखा को समीकरण ax + by + cz = 0 द्वारा दर्शाया जा सकता है। यदि हम a, b, और c को स्तंभ सदिश 'ℓ' और x, y, z को स्तंभ सदिश 'x' मानते हैं तो उपरोक्त समीकरण को आव्यूह रूप में इस प्रकार लिखा जा सकता है:

x^Tℓ = 0 or ℓ^Tx = 0.

सदिश संकेतन का उपयोग करके हम इसके अतिरिक्त x ⋅ ℓ = 0 या ℓ ⋅ x = 0 लिख सकते हैं।

समीकरण k(x^Tℓ) = 0 (जो k एक गैर-शून्य अदिश राशि है) R³ में शून्य से होकर जाने वाले समतल को पार करता है और k(x) एक रेखा को पार करता है, फिर से शून्य से होकर जाता है। समतल और रेखा R³ में रैखिक उपसमष्टि हैं, जो सदैव शून्य से होकर जाता है।

आदर्श बिंदु

P² में एक रेखा का समीकरण ax + by + cz = 0 है और यह समीकरण समीकरण को k से गुणा करके x, y समतल के समानांतर किसी भी तल पर एक रेखा का प्रतिनिधित्व कर सकता है।

यदि z = 1 हमारे समीप सामान्यीकृत सजातीय समन्वय है। z = 1 वाले सभी बिंदु एक समतल बनाते हैं। आइए मान लें कि हम उस तल को देख रहे हैं (z अक्ष के साथ आगे की स्थिति से और मूल की ओर देख रहे हैं) और तल पर दो समांतर रेखाएं खींची गई हैं। जहां से हम खड़े हैं (हमारी दृश्य क्षमताओं को देखते हुए) हम मात्र इतना ही तल देख सकते हैं, जिसे हम आरेख में लाल रंग में उल्लिखित क्षेत्र के रूप में दर्शाते हैं। यदि हम z अक्ष के साथ तल से दूर चलते हैं, (फिर भी पीछे की ओर मूल की ओर देख रहे हैं), तो हम तल के और अधिक देख सकते हैं। हमारे देखने के क्षेत्र में मूल बिंदु स्थानांतरित हो गए हैं। हम सजातीय समन्वय को एक स्थिरांक से विभाजित करके इस गति को प्रतिबिंबित कर सकते हैं। समीपवर्ती प्रतिरूप में हमने 2 से विभाजित किया है इसलिए z मान अब 0.5 हो जाता है। यदि हम अत्याधिक दूर चले जाते हैं तो हम जो देख रहे हैं वह दूरी में एक बिंदु बन जाता है। जैसे-जैसे हम दूर जाते हैं हम अधिक से अधिक समानांतर रेखाएँ देखते हैं। रेखाएँ अनंत पर एक रेखा पर मिलेंगी (एक रेखा जो z = 0 पर तल पर शून्य से होकर जाती है)। तल पर रेखाएँ जब z = 0 आदर्श बिन्दु हैं। z = 0 पर तल अनंत पर रेखा है।

सजातीय बिंदु (0, 0, 0) वह स्थान है जहां सभी वास्तविक बिंदु जाते हैं जब आप तल को अनंत दूरी से देखते हैं, एक रेखा पर z = 0 समतल वह है जहाँ समानांतर रेखाएँ प्रतिच्छेद करती हैं।

द्वैत

समीकरण में x^Tℓ = 0 दो स्तंभ सदिश हैं। आप या तो स्थिर रख सकते हैं और दूसरे को बदल सकते हैं। यदि हम बिंदु x को स्थिर रखते हैं और गुणांक ℓ बदलते हैं तो हम बिंदु से होकर जाने वाली नवीन रेखाएँ बनाते हैं। यदि हम गुणांकों को स्थिर रखते हैं और उन बिंदुओं को बदलते हैं जो समीकरण को संतुष्ट करते हैं तो हम एक रेखा बनाते हैं। हम x को एक बिंदु के रूप में देखते हैं, क्योंकि जिन अक्षों का हम उपयोग कर रहे हैं वे हैं x, y, और z। यदि हम इसके अतिरिक्त 'a', b, c चिह्नित अक्षों का उपयोग करके गुणांकों को प्लॉट करते हैं, तो बिंदु रेखाएँ बन जाएंगे और रेखाएँ बिंदु बन जाएँगी। यदि आप x, y, और z चिह्नित अक्ष पर प्लॉट किए गए डेटा के साथ कुछ साबित करते हैं तो उसी तर्क का उपयोग अक्ष पर प्लॉट किए गए डेटा के लिए a, चिह्नित किया जा सकता है बी , और सी । वह द्वैत है।

बिंदुओं को जोड़ने वाली रेखाएँ और रेखाओं का प्रतिच्छेदन (द्वंद्व का उपयोग करके)

समीकरण x^Tℓ = 0 दो स्तंभ वैक्टर के डॉट उत्पाद की गणना करता है। यदि सदिश ओर्थोगोनल हैं तो दो वैक्टरों का आंतरिक उत्पाद शून्य है। पी में², बिंदु x के बीच की रेखा₁ और एक्स₂ एक स्तंभ सदिश ℓ के रूप में दर्शाया जा सकता है जो समीकरणों को संतुष्ट करता है x₁^Tℓ = 0 और x₂^Tℓ = 0, या दूसरे शब्दों में एक स्तंभ सदिश ℓ जो x के लिए ओर्थोगोनल है₁ और एक्स₂. संकर उत्पाद ऐसे सदिश को खोजेगा: दो बिंदुओं को जोड़ने वाली रेखा में समीकरण द्वारा दिए गए सजातीय निर्देशांक हैं x₁ × x₂. दो रेखाओं का प्रतिच्छेदन उसी तरह से पाया जा सकता है, द्वैत का उपयोग करते हुए, रेखाओं का प्रतिनिधित्व करने वाले वैक्टर के संकर उत्पाद के रूप में, ℓ₁ × ℓ₂.

4-आयामी स्थान में अंतर्निहित करना

प्रक्षेपी तल 4-डायमेंशनल यूक्लिडियन स्थान में अंतर्निहित होता है। वास्तविक प्रक्षेपी तल P²(R) दो-गोले का भागफल स्थान (टोपोलॉजी) है

एस² = {(x, y, z) ∈ 'आर'³ : एक्स² + और² + के साथ² = 1}

प्रतिव्यास संबंध द्वारा (x, y, z) ~ (−x, −y, −z). समारोह पर विचार करें R³ → R⁴ द्वारा दिए गए (x, y, z) ↦ (xy, xz, y² − z², 2yz). यह प्रतिचित्र उस प्रतिचित्र तक सीमित है जिसका डोमेन S है² और, चूंकि प्रत्येक घटक सम कोटि का समांगी बहुपद है, यह R में समान मान लेता है⁴ S पर किन्ही दो प्रतिव्यासांत बिंदुओं में से प्रत्येक पर^{2</उप>। यह एक प्रतिचित्र देता है P2(R) → R4. इसके अलावा, यह प्रतिचित्र एक अंतर्निहित है। ध्यान दें कि यह अंतर्निहित आर में प्रक्षेपण को स्वीकार करता है3 जो रोमन सतह है।}

उच्च गैर-उन्मुख सतहें

क्रमिक रूप से प्रक्षेपी तलों को एक साथ जोड़कर हमें उच्च जीनस (गणित) की गैर-उन्मुख सतहें मिलती हैं। ग्लूइंग प्रक्रिया में प्रत्येक सतह से एक छोटी सी डिस्क को काटना और उनकी सीमा वृत्तों की पहचान (ग्लूइंग) करना शामिल है। दो प्रक्षेपी तलों को चिपकाने से क्लेन की बोतल बनती है।

मौलिक बहुभुज पर लेख उच्च गैर-उन्मुख सतहों का वर्णन करता है।

यह भी देखें

• वास्तविक प्रक्षेप्य स्थान
• प्रक्षेपी स्पेस
• पु की असमानता| वास्तविक प्रक्षेपी तल के लिए पु की असमानता
• चिकना प्रक्षेपी तल

संदर्भ

• Coxeter, H.S.M. (1955), The Real Projective Plane, 2nd ed. Cambridge: At the University Press.
• Reinhold Baer, Linear Algebra and Projective Geometry, Dover, 2005 (ISBN 0-486-44565-8 )
• Richter, David A., Two Models of the Real Projective Plane, retrieved 2010-04-15

बाहरी संबंध

• Weisstein, Eric W. "Real Projective Plane". MathWorld.
• Line field coloring using Werner Boy's real projective plane immersion
• The real projective plane on YouTube