हाइपरबोलाइड मॉडल
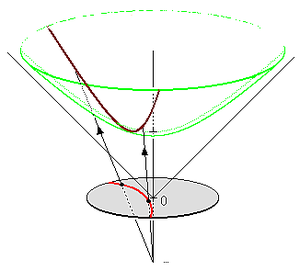
ज्यामिति में, अतिपरवलयज मॉडल, जिसे हरमन मिन्कोव्स्की के बाद मिंकोव्स्की मॉडल के रूप में भी जाना जाता है, 'n'-आयाम अतिपरवलयिक ज्यामिति का एक मॉडल है जिसमें बिंदुओं को फॉरवर्ड शीट S+ पर बिंदुओं द्वारा दर्शाया जाता है (n+1)-आयामी मिन्कोव्स्की समष्टि में या मूल से उन बिंदुओं तक छद्म-यूक्लिडियन समष्टि के विस्थापन वैक्टर द्वारा द्वि पृष्ठी अतिपरवलयज का और m-तलों को (m+1) तलों के प्रतिच्छेदन द्वारा मिन्कोव्स्की समष्टि में S+ के साथ या m वेक्टरों के वेज उत्पादों द्वारा प्रतिनिधित्व किया जाता है। अतिपरवलयिक समष्टि मिन्कोव्स्की समष्टि में सममितीय रूप से अंतःस्थापित किया गया है; अर्थात्, अतिपरवलयिक दूरी फलन मिन्कोव्स्की समष्टि से इन्हेरिटेड में मिला है, जिस तरह से वृत्ताकार दूरी यूक्लिडियन दूरी से इन्हेरिटेड में मिली है, जब n-वृत्त (n+1)-विमीय यूक्लिडियन समष्टि में सन्निहित है।
अतिपरवलयिक समष्टि के अन्य मॉडलों को S+ के मानचित्र अनुमानों के रूप में माना जा सकता है: बेल्ट्रामी-क्लेन मॉडल S+ का प्रक्षेपण (गणित) है मूल से S+ में विशिष्ट बिंदु तक मूल से वेक्टर के लम्बवत तल पर मूल के माध्यम से वृत्त के ग्नोमोनिक प्रक्षेपण के अनुरूप; पॉइंकेयर डिस्क मॉडल अन्य शीट S− पर एक बिंदु के माध्यम से लंबवत तल पर S+ का एक प्रक्षेपण (गणित) है, जो वृत्त के त्रिविम प्रक्षेप प्रक्षेपण के अनुरूप है; गन्स मॉडल S+ का लंबकोणीय प्रक्षेपण है, जो S+ में एक विशिष्ट बिंदु के लंबवत समतल पर है, जो लंबकोणिक मानचित्र प्रक्षेपण के अनुरूप है; अतिपरवलयिक तल का बैंड मॉडल एक अनुरूप "बेलनाकार" प्रक्षेपण है जो वृत्त के मर्केटर प्रक्षेपण के समान है; लोबचेव्स्की निर्देशांक एक बेलनाकार प्रक्षेपण है जो वृत्त के समतुल्य प्रक्षेपण (देशांतर, अक्षांश) के समान है।
मिन्कोव्स्की द्विघात रूप
यदि (x0, x1, ..., xn) (n + 1)-विमीय निर्देशांक समष्टि Rn+1 में एक वेक्टर है, तब मिन्कोव्स्की द्विघात रूप को परिभाषित किया गया है
वेक्टर v ∈ Rn+1 जैसे कि Q(v) = -1 एक n-विमीय अतिपरवलय S बनाता है जिसमें दो जुड़े हुए घटक, या पत्रक होते हैं: अग्र, या भविष्य, पत्रक S+, जहाँ x0<0 और पश्च, या विगत, पत्रक S−, जहाँ x0<0 है। n-आयाम अतिपरवलयज मॉडल के बिंदु फॉरवर्ड शीट S+ पर बिंदु हैं।
मिन्कोव्स्की द्विरेखीय रूप B, मिन्कोव्स्की द्विघात रूप Q का ध्रुवीकरण है,
(इसे कभी-कभी अदिश गुणनफल संकेतन का उपयोग करते हुए भी लिखा जाता है) स्पष्ट रूप से,
S+ के दो बिंदुओं u और v के बीच अतिपरवलयिक दूरी सूत्र द्वारा दिया गया है
जहां चाप अतिपरवलयिक कोज्या का व्युत्क्रम फलन है।
मीट्रिक हस्ताक्षर का विकल्प
द्विरेखीय रूप समष्टि पर मीट्रिक टेंसर के रूप में भी कार्य करता है। n+1 आयामी मिन्कोव्स्की समष्टि में, विपरीत मीट्रिक हस्ताक्षर वाले मीट्रिक के लिए दो विकल्प हैं, 3-आयामी स्थिति में या तो (+, -, -) या (-, +, +) है।
यदि हस्ताक्षर (-, +, +) चयन किया जाता है, तो अतिपरवलयज की एक ही शीट पर अलग-अलग बिंदुओं के बीच जीवाओं का छद्म-यूक्लिडियन समष्टि धनात्मक होगा, जो गणित में पारंपरिक परिभाषाओं और अपेक्षाओं के साथ अधिक निकटता से संरेखित होता है। फिर n-आयाम अतिपरवलयिक समष्टि एक रिमानियन समष्टि है और दूरी या लंबाई को अदिश वर्ग के वर्गमूल के रूप में परिभाषित किया जा सकता है। यदि हस्ताक्षर (+, −, −) चयन किया जाता है, तो अतिपरवलयज पर अलग-अलग बिंदुओं के बीच का अदिश वर्ग ऋणात्मक होगा, इसलिए आधारभूत शब्दों की विभिन्न परिभाषाओं को समायोजित किया जाना चाहिए, जो असुविधाजनक हो सकता है। फिर भी, भौतिकी में समष्टि-समय का वर्णन करने के लिए हस्ताक्षर (+, −, −, −) भी सामान्य है। (Cf. हस्ताक्षर संकेत मैट्रिक हस्ताक्षर।)
सीधी रेखाएँ
अतिपरवलयिक एन-समष्टि में एक सीधी रेखा अतिपरवलयज पर अल्पान्तरी द्वारा तैयार की जाती है। अतिपरवलयज पर अल्पान्तरी n+1-आयामी मिन्कोव्स्की समष्टि के द्वि-आयामी रैखिक उप-समष्टि (मूल सहित) के साथ अतिपरवलयज का (गैर-रिक्त) प्रतिच्छेदन है। यदि हम 'u' और 'v' को उस रैखिक उपसमष्टि के आधार वेक्टरों के रूप में लेते हैं
और अल्पान्तरी पर बिंदुओं के लिए एक वास्तविक पैरामीटर के रूप में w का उपयोग करें
अल्पान्तरी पर एक बिंदु होगा।[1]
अधिक सामान्य रूप से, अतिपरवलयिक n-समष्टि में एक k-आयाम समतल अतिपरवलयज के (गैर-रिक्त) प्रतिच्छेदन द्वारा मिंकोव्स्की समष्टि के k+1-आयाम रैखिक उपसमष्टि (मूल सहित) के साथ तैयार किया जाएगा।
समदूरीकता
अनिश्चितकालीन लंबकोणीय समूह O(1,n), को भी कहा जाता है (n+1)-विमीय लॉरेंत्ज़ समूह, वास्तविक संख्या (n+1)×(n+1) आव्यूह (गणित) का लाई समूह है जो मिन्कोव्स्की द्विरेखीय रूप को संरक्षित करता है। एक अलग भाषा में, यह मिन्कोव्स्की समष्टि के रैखिक समरूपता का समूह है। विशेष रूप से, यह समूह अतिपरवलयज S को संरक्षित करता है। याद रखें कि अनिश्चित लंबकोणीय समूहों में चार जुड़े घटक होते हैं, जो प्रत्येक उप-समष्टि (यहां 1-आयामी और n-आयामी) पर अभिविन्यास को उलटने या संरक्षित करने के अनुरूप होते हैं, और क्लेन चार-समूह बनाते हैं। O(1,n) का उपसमूह जो पहले निर्देशांक के चिह्न को संरक्षित करता है, 'ऑर्थोक्रोनस लोरेंत्ज़ समूह,' है, जिसे O+(1,n) निरूपित किया गया है।, और इसके दो घटक हैं, समष्टिक उप-समष्टि के अभिविन्यास को संरक्षित करने या उत्क्रम के अनुरूप है। इसका उपसमूह SO+(1,n) एक निर्धारक के साथ आव्यूह से मिलकर आयाम n(n+1)/2 का जुड़ा हुआ समूह है जो S+ पर कार्य करता है रैखिक स्वसमाकृतिकता द्वारा और अतिपरवलयिक दूरी को संरक्षित करता है। यह क्रिया सकर्मक है और वेक्टर के स्थिरक (1,0,...,0) में आव्यूह के रूप मे सम्मिलित होते हैं
जहाँ सुसंहत विशेष लंबकोणीय समूह SO(n) के अंतर्गत आता है (घूर्णन समूह SO(3) (3) को सामान्य बनाने के लिए n = 3) यह इस प्रकार है कि n-आयाम अतिपरवलयिक समष्टि को सजातीय समष्टि और श्रेणी 1 के रिमेंनियन सममित समष्टि के रूप में प्रदर्शित किया जा सकता है,
समूह SO+(1,n) n-आयाम अतिपरवलयिक समष्टि के अभिविन्यास-संरक्षण समदूरीकता का पूरा समूह है।
अधिक मूर्त शब्दों में, SO+(1,n) को n(n-1)/2 घुमावों में विभाजित किया जा सकता है (निचले-दाएं ब्लॉक में एक नियमित यूक्लिडियन घूर्णन आव्यूह के साथ गठित) और n अतिपरवलयिक स्थानांतरण, जो रूप लेते हैं
जहाँ स्थानांतरणित दूरी है (इस स्थिति में x अक्ष के साथ), और दूसरी पंक्ति/स्तंभ को एक अलग जोड़ी के साथ एक अलग अक्ष के साथ स्थानांतरण में बदलने के लिए आदान-प्रदान किया जा सकता है। वेक्टर के साथ 3 आयामों में स्थानांतरण का सामान्य रूप है:
- जहाँ .
यह स्वाभाविक रूप से अधिक आयामों तक विस्तारित होता है, और जब आप सापेक्षता-विशिष्ट शर्तों को हटाते हैं तो यह लोरेंत्ज़ रूपांतरण उपयुक्त रूपांतरणों का सरलीकृत संस्करण भी होता है।
समदूरीकता के समूहों के उदाहरण
अतिपरवलयज मॉडल के सभी समदूरीकता का समूह O+(1,n ) है समदूरीकता का कोई भी समूह इसका एक उपसमूह है।
प्रतिबिंब
दो अंक के लिए , उनका आदान-प्रदान करने वाला एक अद्वितीय प्रतिबिंब है।
मान लीजिए . ध्यान दें कि , और इसलिए .
तब
एक प्रतिबिंब है जो आदान-प्रदान करता है और . यह निम्नलिखित आव्यूह के बराबर है:
(ब्लॉक आव्यूह संकेतन के उपयोग पर ध्यान दें)।
तब समदूरीकता का एक समूह है। ऐसे सभी उपसमूह संयुग्मी वर्ग उपसमूहों और सामान्य उपसमुच्चयों की संयुग्मता हैं।
घूर्णन और प्रतिबिंब
घूर्णन और परावर्तनों का समूह है जो संरक्षित करता है फलन इस समूह के लिए लंबकोणीय समूह O(n) से एक समूह समरूपता है। किसी भी बिंदु के लिए , यदि एक समदूरीकता है जो को मानचित्रण करती है तब घूर्णनों और परावर्तनों का समूह है जो संरक्षित करता है।
स्थानांतरण
किसी भी वास्तविक संख्या के लिए , एक स्थानांतरण है
यह दूरी का स्थानांतरण है धनात्मक x दिशा में यदि या दूरी का नकारात्मक x दिशा में यदि दूरी का कोई भी स्थानांतरण से संयुग्मित और समुच्चय x-अक्ष के माध्यम से स्थानांतरण का समूह है, और समदूरीकता का एक समूह इसके साथ संयुग्मित है यदि और केवल यदि यह एक रेखा के माध्यम से समदूरीकता का समूह है।
उदाहरण के लिए, मान लें कि हम एक पंक्ति के माध्यम से स्थानांतरणों के समूह को खोजना चाहते हैं मान लीजिए एक समदूरीकता बनें जो को प्रतिचित्रण करता है और एक समदूरीकता बनें जो परिशुद्ध करता है और मानचित्र को द्वारा प्रतिचित्रण करता है एक ऐसा उदाहरण एक प्रतिबिंब विनिमय है और (यह मानते हुए कि वे भिन्न हैं), क्योंकि वे दोनों एक ही दूरी से हैं तब एक समदूरीकता को और धनात्मक x-अक्ष पर एक बिंदु प्रतिचित्रण है पंक्ति के माध्यम से दूरी का स्थानांतरण है यदि , वह उस दिशा में है। यदि , वह दिशा में है। तब के माध्यम से स्थानांतरण का समूह है।
राशिफल की समरूपता
मान लीजिए H कुछ होरोस्फीयर (राशिफल) है जैसे प्रारूप के बिंदु एकपक्षीय रूप से बड़े x के लिए इसके अंदर हैं। किसी भी वेक्टर b के लिए
एक होरोरोटेशन है जो H को स्वयं से प्रतिचित्रण करता है। इस तरह के होरोरोटेशन का समुच्चय H को संरक्षित करने वाले होरोरोटेशन का समूह है। सभी हॉरोटेशन एक दूसरे से संयुग्मित होते हैं।
किसी के लिए में O(n-1)
एक घूर्णन या प्रतिबिंब है जो H और x -अक्ष को संरक्षित करता है। ये होरोरोटेशन, घूर्णन और प्रतिबिंब H के समरूपता के समूह को उत्पन्न करते हैं। किसी भी होरोस्फीयर का समरूपता समूह इसके साथ संयुग्मित होता है। वे यूक्लिडियन समूह E(n-1) के समरूपी हैं।
इतिहास
1878-1885 के बीच कई पत्रों में, विल्हेम किलिंग[2][3][4] लोबचेवस्कियन ज्यामिति के लिए उन्होंने कार्ल वीयरस्ट्रास को अधीन प्रतिनिधित्व का उपयोग किया। विशेष रूप से, उन्होंने द्विघात रूपों पर चर्चा की जैसे या एकपक्षीय आयामों में , जहाँ वक्रता का पारस्परिक माप है, यूक्लिडियन ज्यामिति, अण्डाकार ज्यामिति, और अतिपरवलयिक ज्यामिति को दर्शाता है।
जेरेमी ग्रे (1986) के अनुसार,[5] हेनरी पोंकारे ने 1880 में अपने व्यक्तिगत नोट्स में अतिपरवलयज मॉडल का उपयोग किया। पोंकारे ने 1881 में अपने परिणाम प्रकाशित किए, जिसमें उन्होंने द्विघात रूप के व्युत्क्रम पर चर्चा की [6] ग्रे दिखाता है कि पोनकारे द्वारा बाद के लेखन में अतिपरवलयज मॉडल निहित है।[7]
इसके अतिरिक्त 1882 में होमर्शम कॉक्स (गणितज्ञ)।[8][9] उपयोग किए गए वीयरस्ट्रैस निर्देशांक (इस नाम का उपयोग किए बिना) संबंध को साथ ही को पूर्ण करते हैं
1891 में अल्फ्रेड क्लेब्सच और फर्डिनेंड लिंडमैन द्वारा मॉडल के आगे के संबंध और पर चर्चा की गई।[10]
जेरार्ड (1892),[11] फेलिक्स हॉसडॉर्फ (1899),[12] फ्रेडरिक एस. वुड्स (1903)],[13] हेनरिक लिबमैन (1905) द्वारा वीयरस्ट्रास निर्देशांक का भी उपयोग किया गया था।[14]
समष्टि विश्लेषण में अपने पत्र (1894) में अलेक्जेंडर मैकफर्लेन द्वारा अतिपरवलयज को एक मीट्रिक समष्टि के रूप में खोजा गया था। उन्होंने नोट किया कि अतिपरवलयज पर बिन्दुओं को इस प्रकार लिखा जा सकता है
जहां α अतिपरवलय अक्ष के लिए एक आधार सदिश लंबकोणीय है। उदाहरण के लिए, उन्होंने अपने भौतिकी के बीजगणित के उपयोग के माध्यम से कोसाइन के अतिपरवलयिक नियम को प्राप्त किया।[1]
एच. जानसन ने अतिपरवलयज मॉडल को अपने 1909 के पेपर ''रिप्रेजेंटेशन ऑफ़ हाइपरबोलिक ज्योमेट्री ऑन ए टू शीटेड हाइपरबोलॉइड'' का स्पष्ट केंद्र बनाया।[15] 1993 में डब्ल्यू.एफ. रेनॉल्ड्स ने अमेरिकन मैथमैटिकल मंथली में अपने लेख में मॉडल के कुछ प्रारम्भिक इतिहास का वर्णन किया।[16]
बीसवीं शताब्दी तक एक सामान्य मॉडल होने के बाद, इसकी पहचान 1907 में गोटिंगेन व्याख्यान 'द रिलेटिविटी प्रिंसिपल' में हरमन मिन्कोव्स्की द्वारा गेशविंडिग्केइट्सवेक्टरन (वेग वैक्टर) के साथ की गई थी। स्कॉट वाल्टर, अपने 1999 के पेपर द नॉन-यूक्लिडियन स्टाइल ऑफ़ मिंकोव्स्की रिलेटिविटी में[17] मिन्कोव्स्की की अभिज्ञता को खण्डन करते हैं, लेकिन वेइरस्ट्रास और किलिंग के अतिरिक्त मॉडल के परंपरा को हरमन हेल्महोल्ट्ज़ के लिए पता लगाते हैं।
सापेक्षता के प्रारम्भिक वर्षों में वेग की भौतिकी की व्याख्या करने के लिए व्लादिमीर वरिकैक द्वारा अतिपरवलयज मॉडल का उपयोग किया गया था। 1912 में जर्मन गणितीय संघ के अपने भाषण में उन्होंने वेइरस्ट्रास निर्देशांकों का उल्लेख किया।[18]
यह भी देखें
- पॉइनकेयर डिस्क मॉडल
- अतिपरवलयिक चतुष्कोण
नोट्स और संदर्भ
- ↑ 1.0 1.1 Alexander Macfarlane (1894) Papers on Space Analysis, B. Westerman, New York, weblink from archive.org
- ↑ Killing, W. (1878) [1877]. "Ueber zwei Raumformen mit constanter positiver Krümmung". Journal für die Reine und Angewandte Mathematik. 86: 72–83.
- ↑ Killing, W. (1880) [1879]. "गैर-यूक्लिडियन स्थानिक रूपों में गणना". Journal für die Reine und Angewandte Mathematik. 89: 265–287.
- ↑ Killing, W. (1885). गैर-यूक्लिडियन स्थानिक रूप. Leipzig.
{{cite book}}: CS1 maint: location missing publisher (link) - ↑ Linear differential equations and group theory from Riemann to Poincaré (pages 271,2)
- ↑ Poincaré, H. (1881). "Sur les applications de la géométrie non-euclidienne à la théorie des formes quadratiques" (PDF). Association Française Pour l'Avancement des Sciences. 10: 132–138.
- ↑ See also Poincaré: On the fundamental hypotheses of geometry 1887 Collected works vol.11, 71-91 and referred to in the book of B.A. Rosenfeld A History of Non-Euclidean Geometry p.266 in English version (Springer 1988).
- ↑ Cox, H. (1881). "काल्पनिक ज्यामिति में सजातीय निर्देशांक और बलों की प्रणालियों के लिए उनका अनुप्रयोग". The Quarterly Journal of Pure and Applied Mathematics. 18 (70): 178–192.
- ↑ Cox, H. (1882) [1881]. "काल्पनिक ज्यामिति में सजातीय निर्देशांक और बलों की प्रणालियों के लिए उनका अनुप्रयोग (जारी)". The Quarterly Journal of Pure and Applied Mathematics. 18 (71): 193–215.
- ↑ Lindemann, F. (1891) [1890]. Vorlesungen über Geometrie von Clebsch II. Leipzig. p. 524.
{{cite book}}: CS1 maint: location missing publisher (link) - ↑ Gérard, L. (1892). Sur la géométrie non-Euclidienne. Paris: Gauthier-Villars.
- ↑ Hausdorff, F. (1899). "Analytische Beiträge zur nichteuklidischen Geometrie". Leipziger Math.-Phys. Berichte. 51: 161–214. hdl:2027/hvd.32044092889328.
- ↑ Woods, F. S. (1905) [1903]. "गैर-यूक्लिडियन अंतरिक्ष के रूप". The Boston Colloquium: Lectures on Mathematics for the Year 1903: 31–74.
- ↑ Liebmann, H. (1905) [1904]. गैर-यूक्लिडियन ज्यामिति. Leipzig: Göschen.
- ↑ Abbildung hyperbolische Geometrie auf ein zweischaliges Hyperboloid Mitt. Math. Gesellsch Hamburg 4:409–440.
- ↑ Reynolds, William F. (1993) "Hyperbolic geometry on a hyperboloid", American Mathematical Monthly 100:442–55, Jstor link
- ↑ Walter, Scott A. (1999), "The non-Euclidean style of Minkowskian relativity", in J. Gray (ed.), The Symbolic Universe: Geometry and Physics 1890-1930, Oxford University Press, pp. 91–127
- ↑ Varićak, V. (1912), , Jahresbericht der Deutschen Mathematiker-Vereinigung, 21: 103–127
- Alekseevskij, D.V.; Vinberg, E.B.; Solodovnikov, A.S. (1993), Geometry of Spaces of Constant Curvature, Encyclopaedia of Mathematical Sciences, Berlin, New York: Springer-Verlag, ISBN 978-3-540-52000-9
- Anderson, James (2005), Hyperbolic Geometry, Springer Undergraduate Mathematics Series (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-1-85233-934-0
- Ratcliffe, John G. (1994), Foundations of hyperbolic manifolds, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94348-0, अध्याय 3
- माइल्स रीड एंड बालाज़ सज़ेंड्रोई (2005) ज्यामिति और टोपोलॉजी, चित्र 3.10, पृष्ठ 45, कैम्ब्रिज यूनिवर्सिटी प्रेस, ISBN 0-521-61325-6, MR2194744.
- Ryan, Patrick J. (1986), Euclidean and non-Euclidean geometry: An analytical approach, Cambridge, London, New York, New Rochelle, Melbourne, Sydney: Cambridge University Press, ISBN 978-0-521-25654-4
- Parkkonen, Jouni. "अतिशयोक्तिपूर्ण ज्यामिति" (PDF). Retrieved September 5, 2020.
{{cite web}}: CS1 maint: url-status (link)
श्रेणी:बहुआयामी ज्यामिति श्रेणी:अतिपरवलयिक ज्यामिति श्रेणी:मिन्कोस्की समष्टिटाइम