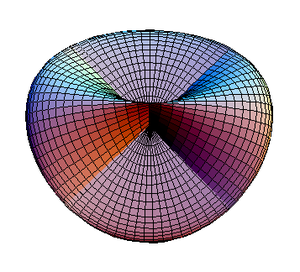
रोमन सतह
गणित में, रोमन सतह या स्टेनर सतह असाधारण रूप से उच्च स्तर की समरूपता के साथ त्रि-आयामी स्थान में वास्तविक प्रक्षेपी तल का एक स्व-प्रतिच्छेदन मानचित्र (गणित) है। यद्दपि, एक वक्र के छह विलक्षण बिंदुओं को हटाने से उत्पन्न होने वाला आंकड़ा एक है,तो यह वास्तविक प्रक्षेपी तल का निमज्जन (गणित) नहीं है। इसका नाम इसलिए पड़ा क्योंकि इसकी खोज जैकब स्टेनर ने की थी जब वह 1844 में रोम में थे। [1]
सबसे सरल निर्माण मानचित्र के नीचे उत्पत्ति पर केंद्रित क्षेत्र की छवि के रूप में है यह का एक निहित सूत्र देता है
साथ ही, देशांतर रेखा के संदर्भ में गोले का मानकीकरण लेना (θ) और अक्षांश (φ), रोमन सतह के लिए निम्नानुसार प्राचलिक समीकरण देता है:
मूल एक त्रिपक्षीय बिंदु है, और प्रत्येक xy-, yz-, और xz-तल वहां की सतह के स्पर्शरेखा होते हैं। स्व-प्रतिच्छेदन के अन्य स्थान दोहरे बिंदु हैं,जो प्रत्येक समन्वय अक्ष के साथ खंडों को परिभाषित करते हैं जो छह पिंच बिंदुओं में समाप्त होते हैं। यह पूरी सतह में चतुर्पाश्वीय समरूपता समूह है। यह स्टेनर सतह का एक विशेष प्रकार (जिसे टाइप 1 कहा जाता है) है, जो कि वेरोनीज़ सतह का 3-आयामी रैखिक प्रक्षेपण है।
अंतर्निहित सूत्र की व्युत्पत्ति
सरलता के लिए हम केवल स्थिति r = 1 पर विचार करते हैं। बिंदु (x, y, z) द्वारा परिभाषित गोले को इस प्रकार दिया गया है कि
हम इन बिंदुओं पर परिवर्तन T द्वारा परिभाषित करते हैं
लेकिन फिर हमारे पास है
इसलिए जैसी शर्त थी।
इसके विपरीत, मान लीजिए कि हमें (U, V, W) संतोषजनक दिया गया है
(*)
हम प्रमाणित करते हैं कि उपस्थित (x,y,z) ऐसा है कि
(**)
जिसके लिए
एक अपवाद के साथ: प्रकरण में 3.बी। नीचे, हम दिखाते हैं कि यह प्रमाणित नहीं किया जा सकता है।
1. ऐसे प्रकरण में जहां U, V, W में से कोई भी 0 नहीं है, हम रख सकते हैं
(ध्यान दें कि (*) इस बात की गारंटी देता है कि या तो U, V, W के तीनों सकारात्मक हैं, या फिर ठीक दो ऋणात्मक हैं। इसलिए ये वर्गमूल धनात्मक संख्याओं के हैं। )
यह पुष्टि करने के लिए (*) का उपयोग करना सरल है कि (**) x, y, z के लिए इस तरह से परिभाषित है।
2. मान लीजिए कि W 0 है। (*) से इसका तात्पर्य है
और इसलिए U, V में से कम से कम एक को भी 0 होना चाहिए। इससे पता चलता है कि क्या U, V, W में से किसी एक का 0 होना असंभव है।
3. मान लीजिए कि U, V, W में से ठीक दो 0 हैं। व्यापकता को खोए बिना हम मान लेते हैं
(***)
यह इस प्रकार है कि
(तब से इसका आशय है और इसलिए विरोधाभासी (***)। )
a. एक उप-प्रकरण में जहां
अगर हम x और y द्वारा निर्धारित करते हैं
और
यह सुनिश्चित करता है कि (*) धारण करता है। इसे सत्यापित करना सरल है
और इसलिए x और y के चिह्नों को उचित रूप से चुनना गारंटी देगा
चूंकि भी
इससे पता चलता है कि यह उपप्रकरण वांछित हल की ओर ले जाता है।
b. प्रकरण 3 के इस शेष उपप्रकरण में, हमारे पास है
तब से
इसे सुनिश्चित करना सरल है
और इस प्रकार इस प्रकरण में, जहां
कोई (x, y, z) संतोषजनक नहीं है
इसलिए समीकरण (*) के समाधान (U, 0, 0) के साथ
और इसी तरह, (0, V, 0) के साथ
और (0, 0, W) के साथ
(जिनमें से प्रत्येक दो टुकड़ों में एक समन्वय अक्ष का एक गैर-सुगठित भाग है) रोमन सतह पर किसी भी बिंदु के अनुरूप नहीं है।
4. यदि (U, V, W) बिंदु (0, 0, 0) है, तो यदि x, y में से कोई दो, z शून्य हैं और तीसरे का पूर्ण मान 1 है, स्पष्ट रूप से जैसी शर्त थी।
इसमें सभी संभावित प्रकरणों को सम्मिलित किया गया है।
प्राचलिक समीकरणों की व्युत्पत्ति
मान लीजिए एक गोले की त्रिज्या r, देशांतर φ और अक्षांश θ है। फिर इसके प्राचलिक समीकरण हैं
फिर, इस गोले के सभी बिंदुओं पर परिवर्तन T लागू करने से प्राप्त होता है
जो रोमन सतह पर बिंदु हैं। मान लीजिए φ का परिसर 0 से 2π तक है, और θ का परिसर 0 से π/2 तक है।
वास्तविक प्रक्षेपी तल से संबंध
वृत्त, रूपांतरित होने से पहले, वास्तविक प्रक्षेपी तल, RP2 के लिए होमियोमोर्फिज्म नहीं है। लेकिन मूल बिंदु पर केंद्रित क्षेत्र में यह संपत्ति है,कि यदि बिंदु (x, y, z) क्षेत्र से संबंधित है,तो प्रतिलोमी संबंधी बिंदु (-x, -y, -z) और ये दो बिंदु अलग है: वे गोले के केंद्र के विपरीत दिशा में रहें।
रूपांतरण T इन दोनों प्रतिलोमी संबंधी बिंदुओं को एक ही बिंदु में परिवर्तित करता है,
चूँकि यह S2 के सभी बिंदुओं के लिए सत्य है, तो यह स्पष्ट है कि रोमन सतह एक गोलाकार सापेक्ष प्रतिलोम की एक सतत छवि है। क्योंकि प्रतिलोम के कुछ अलग जोड़े सभी रोमन सतह में समान बिंदुओं पर ले जाए जाते हैं, यह RP2 के लिए होमियोमॉर्फिक नहीं है, लेकिन इसके बजाय वास्तविक प्रक्षेपी तल RP2 का भागफल है = S2 / (x~-x) इसके अलावा,मानचित्र T (ऊपर) S2 से भागफल के लिए विशेष संपत्ति है कि यह स्थानीय रूप से प्रतिलोम-संबंधी बिंदुओं के छह जोड़े से दूर अंतःक्षेपक है। या RP2 से परिणामी मानचित्र इसे RP2 का निमज्जन बनाता है-- माइनस छह पॉइंट-- 3 स्थान में।
(यह पहले कहा गया था कि रोमन सतह RP2 के लिए होमोमोर्फिक है, लेकिन यह गलती से हुआ था। बाद में यह कहा गया कि रोमन सतह RP2 का निमज्जन है R3 में, लेकिन वह भी त्रुटि में था। )[citation needed]
रोमन सतह की संरचना
रोमन सतह में चार बल्बनुमा पालियां होती हैं, प्रत्येक एक चतुर्पाश्वीय के एक अलग कोने पर होता है।
एक रोमन सतह का निर्माण तीन ठोस अनुवृत्त को एक साथ जोड़कर और फिर आवश्यक रूप से किनारों को चिकना करके किया जा सकता है जिससे कि यह एक वांछित आकार (जैसे मानकीकरण) में उपयुक्त हो सके।
ये तीन अतिपरवलिक ठोस अनुवृत्त होने दें:
- x = yz,
- y = zx,
- z = xy.
ये तीन अतिपरवलिक ठोस अनुवृत्त एक चतुर्पाश्वीय के छह किनारों के साथ बाहरी रूप से और तीन अक्षों के साथ आंतरिक रूप से प्रतिच्छेद करते हैं। आंतरिक प्रतिच्छेदन दोहरे बिंदुओं के स्थान हैं। दोहरे बिंदुओं के तीन बिंदुपथ: x = 0, y = 0, और z = 0, उत्पत्ति (गणित) पर एक तिहरे बिंदु पर प्रतिच्छेद करते हैं।
उदाहरण के लिए, दिया गया x = yz और y = zx, दूसरा परवलयज x = y/z के बराबर है। तब
और या तो y = 0 या z2 = 1 ताकि z = ±1. उनके दो बाहरी प्रतिच्छेदन हैं
- x = y, z = 1.
- x = -y, z = -1.
इसी तरह, अन्य बाहरी प्रतिच्छेदन हैं
- x = z, y = 1
- x = -z, y = -1;
- y = z, x = 1
- y = -z, x = -1.
आइए देखते हैं टुकड़ों को एक साथ रखा जा रहा है। परवलयजों y = xz और x = yz को मिलाइए। परिणाम चित्र 1 में दिखाया गया है।
ठोस अनुवृत्त y = x z को नीले और नारंगी रंग में दिखाया गया है। परवलयज x = y z को सियान और बैंगनी रंग में दिखाया गया है। छवि में परवलयज z = 0 अक्ष के साथ प्रतिच्छेद करते हुए दिखाई देते हैं। यदि परवलयज विस्तारित होते हैं, तो उन्हें रेखाओं के साथ प्रतिच्छेद करते हुए भी देखा जाना चाहिए
- z = 1, y = x
- z = -1, y = -x.
एक साथ दो परवलयज एक साथ आर्किड की एक जोड़ी की तरह दिखते हैं।
अब उनके माध्यम से तीसरा अतिपरवलयिक परवलयज, z = xy, चलाएँ। परिणाम चित्र 2 में दिखाया गया है।
चित्र 2 में पश्चिम-दक्षिण-पश्चिम और पूर्व-उत्तर-पूर्व दिशाओं में एक जोड़ी द्वार हैं। ये आरंभिक पालीयां हैं और इन्हें बंद करने की आवश्यकता है। जब द्वार बंद हो जाते हैं, तो परिणाम चित्र 3 में दिखाई गई रोमन सतह है।
चित्र 3 के पश्चिम और पूर्व दिशाओं में पालियों की एक जोड़ी देखी जा सकती है। पालियों की एक और जोड़ी तीसरे (z = xy) परवलय के नीचे छिपी हुई है और उत्तर और दक्षिण दिशाओं में स्थित है।
यदि तीन अन्तर्विभाजक अतिपरवलयिक परवलयज इतनी दूर खींचे जाते हैं कि वे चतुष्फलक के किनारों के साथ प्रतिच्छेद करते हैं, तो परिणाम चित्र 4 में दिखाया गया है।
पालियों में से एक को चित्र 4 में सामने-सिर पर-दिखाया गया है। पालीयों को चतुर्पाश्वीय के चार कोनों में से एक के रूप में देखा जा सकता है।
यदि चित्र 4 में निरंतर सतह के नुकीले किनारे गोलाकार हैं—चिकना कर दिए गए हैं—तो परिणाम चित्र 5 में रोमन सतह है।
चित्र 5 में रोमन सतह के पालियों में से एक को सामने से देखा गया है, और इसका प्रकाश बल्ब - गुब्बारे जैसा - आकार स्पष्ट है।
यदि चित्र 5 में सतह को 180 डिग्री के आसपास घुमाया जाता है और फिर उल्टा कर दिया जाता है, तो परिणाम चित्र 6 में दिखाया गया है।
चित्र 6 में तीन पालियों को बग़ल में देखा गया है। पालियों की प्रत्येक जोड़ी के बीच एक समन्वय अक्ष के अनुरूप दोहरे बिंदुओं का स्थान होता है। तीन बिंदुपथ मूल बिंदु पर एक तिहरे बिंदु पर प्रतिच्छेद करते हैं। चौथी पालि छिपा हुई है और सीधे दर्शक के विपरीत दिशा में इंगित करती है। इस लेख के शीर्ष पर दिखाई गई रोमन सतह में भी तिरछे दृश्य में तीन पालियाँ हैं।
एकदिशीय
रोमन सतह गैर-उन्मुख है, अर्थात एकदिशीय है। यह बिल्कुल स्पष्ट नहीं है। इसे देखने के लिए, चित्र 3 को फिर से देखें।
तीसरे अतिपरवलयिक परवलयज, z = xy के शीर्ष पर एक प्रतिरोधी की कल्पना करें। इस प्रतिरोधी को उत्तर की ओर चलने दो। जैसे-जैसे यह चलता है, यह अन्य दो परवलयों से होकर गुजरेगा, जैसे कोई प्रतिच्छाया दीवार से गुजरती है। ये अन्य परवलय केवल निमज्जन की स्व-प्रतिच्छेदी प्रकृति के कारण बाधाओं की तरह प्रतीत होते हैं। प्रतिरोधी को सभी दोहरे और तिहरे बिंदुओं को अन्देखा करने दें और सीधे उनके बीच से गुज़रें। तो प्रतिरोधी उत्तर की ओर बढ़ता है और बोलने के लिए दुनिया के किनारे से गिर जाता है। अब यह खुद को उत्तरी पालीयों पर पाता है, जो चित्र 3 के तीसरे परवलय के नीचे छिपा हुआ है। प्रतिरोधी रोमन सतह के बाहर उल्टा खड़ा है।
प्रतिरोधी को नैऋत्य दिशा की ओर चलने दें। यह एक ढलान (उल्टा-नीचे) पर तब तक चढ़ेगा जब तक कि यह खुद को पश्चिमी पालि के अंदर नहीं पाता। अब प्रतिरोधी को दक्षिण-पूर्वी दिशा में पश्चिमी पालियों के अंदर z = 0 अक्ष की ओर, हमेशा x-y तल के ऊपर चलने दें। जैसे ही यह z = 0 अक्ष से गुजरता है, प्रतिरोधी पूर्वी पालियों के बाहर की ओर होगा, दाहिनी ओर खड़ा होगा।
फिर इसे उत्तर की ओर, पहाड़ी के ऊपर, फिर उत्तर-पश्चिम की ओर बढ़ने दें ताकि यह x = 0 अक्ष की ओर खिसकने लगे। जैसे ही प्रतिरोधी इस अक्ष को पार करता है, वह अपने आप को उत्तरी पालि के अंदर, दाहिनी ओर ऊपर की ओर खड़ा पाएगा। अब प्रतिरोधी को उत्तर दिशा की ओर चलने दें। यह दीवार पर चढ़ेगा, फिर उत्तरी पालि की छत के साथ चढ़ेगा। प्रतिरोधी तीसरे अतिपरवलिक परवलयज पर वापस आ गया है, लेकिन इस बार इसके नीचे और उल्टा खड़ा है। (क्लीन बोतल से तुलना करें। )
दोहरे, तिहरे, और पिंचिंग बिंदु
रोमन सतह में चार पालियाँ होती हैं। प्रत्येक पालियों की सीमाएं दोहरे बिंदुओं की तीन पंक्तियों का एक समूह हैं। पालियों की प्रत्येक जोड़ी के बीच दोहरे बिंदुओं की एक रेखा होती है। सतह में दोहरे बिंदुओं की कुल तीन रेखाएँ होती हैं, जो निर्देशांक अक्षों पर स्थित होती हैं (पहले दिए गए मानकीकरण में)। दोहरे बिंदुओं की तीन रेखाएँ एक तिहरे बिंदु पर प्रतिच्छेद करती हैं जो मूल पर स्थित है। त्रिक बिंदु दोहरे बिंदुओं की रेखाओं को अर्ध-रेखाओं की एक जोड़ी में काटता है, और प्रत्येक अर्ध-रेखा पालियों की एक जोड़ी के बीच स्थित होती है। पिछले कथनों से आशा की जा सकती है कि अंतरिक्ष के प्रत्येक अष्टक में एक आठ पालियां हो सकती हैं, जिसे समन्वय विमानों द्वारा विभाजित किया गया है। लेकिन पालियां बारी-बारी से अष्टक पर कब्जा कर लेती हैं: चार अष्टक खाली होते हैं और चार पलियों के कब्जे में होते हैं।
यदि रोमन सतह को चतुर्पाश्वीय के अंदर कम से कम संभावित आयतन के साथ अंकित किया जाता है, तो कोई यह पाएगा कि चतुर्पाश्वीय का प्रत्येक किनारा एक बिंदु पर रोमन सतह पर स्पर्शरेखा है, और इन छह बिंदुओं में से प्रत्येक एक व्हिटनी गणितीय विलक्षणता है। ये विलक्षणताएं, या पिंचिंग बिंदु, सभी दोहरे बिंदुओं की तीन पंक्तियों के किनारों पर स्थित हैं, और उन्हें इस संपत्ति द्वारा परिभाषित किया गया है: कि विलक्षणता पर किसी भी सतह पर कोई समतल स्पर्शरेखा स्थान नहीं है।
यह भी देखें
- लड़के की सतह - क्रॉस-कैप्स के बिना प्रक्षेपीय तल का एक एम्बेडिंग
- टेट्राहेमीहेक्साइड्रोन - रोमन सतह के समान एक बहुफलक।
संदर्भ
- ↑ Coffman, Adam. "स्टाइनर रोमन सतहों". National Curve Bank. Indiana University - Purdue University Fort Wayne.
सामान्य संदर्भ
- एक। कॉफमैन, ए. श्वार्ट्ज, और सी. स्टैंटन: द अलजेब्रा एंड ज्योमेट्री ऑफ स्टेनर एंड अदर क्वाड्रैटिकली पैरामीट्रिजेबल सरफेस। कंप्यूटर एडेड जियोमेट्रिक डिज़ाइन में (3) 13 (अप्रैल 1996), पी। 257-286
- बर्ट जुट्लर, रागी पिएन: जियोमेट्रिक मॉडलिंग और बीजगणितीय ज्यामिति। स्प्रिंगर 2008, ISBN 978-3-540-72184-0, पी। 30 (restricted online copy, p. 30, at Google Books)
बाहरी संबंध
- A. Coffman, "Steiner Surfaces"
- Weisstein, Eric W. "Roman Surface". MathWorld.
- Roman Surfaces at the National Curve Bank (website of the California State University)
- Ashay Dharwadker, Heptahedron and Roman Surface, Electronic Geometry Models, 2004.