फोर्ड वृत्त

1 से 20 तक q के लिए Ford सर्कल। q ≤ 10 वाले सर्कल को लेबल किया गया है p/q और क्यू के अनुसार रंग-कोडित। प्रत्येक वृत्त आधार रेखा और उसके पड़ोसी वृत्तों की स्पर्शरेखा है। समान भाजक वाले इरेड्यूसिबल अंशों में समान आकार के वृत्त होते हैं।

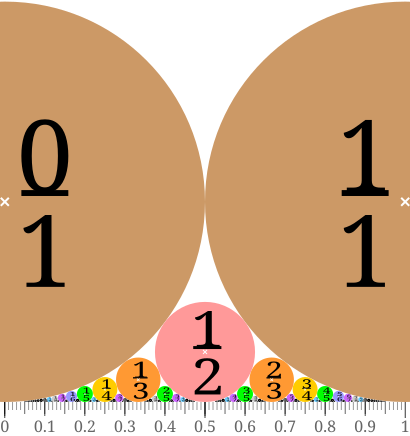
गणित में युक्लीडियन ताल में फोर्ड वृत्त है वृत्त के परिवार में परिमेय बिंदुओं पर एक्स-एक्सिस की सभी स्पर्श रेखाएं होती हैं। प्रत्येक परिमेय संख्या p/q के लिए, निम्नतम शब्दों में व्यक्त किया गया, फोर्ड वृत्त है जिसका केंद्र बिंदु $(p/q,1/(2q^{2}))$ पर है और जिसकी त्रिज्या $1/(2q^{2})$है।यह अपने निचले बिंदु,$(p/q,0)$ पर सी-अक्ष पर स्पर्शरेखा है। परिमेय संख्या $p/q$ और $r/s$ (दोनों निम्नतम शब्दों में) के लिए दो फोर्ड वृत्त स्पर्शरेखा है जब $|ps-qr|=1$ और अन्यथा ये दो वृत्त अलग हैं।

इतिहास

फोर्ड सर्किल परस्पर स्पर्शरेखा वृत्त का विशेष कारण है; आधार रेखा को अनंत त्रिज्या वाले वृत्त के रूप में माना जा सकता है। पेरगा के एपोलोनियस द्वारा पारस्परिक रूप से स्पर्शरेखा वृतों की प्रणालियों का अध्ययन किया गया, जिसके बाद एपोलोनियस और अपोलोनियन गैसकेट की समस्या का नाम दिया गया है। 17वीं शताब्दी में रेने डेसकार्टेस ने डेसकार्टेस प्रमेय की खोज की, जो पारस्परिक रूप से स्पर्शरेखा वाले वृतों की त्रिज्या के व्युत्क्रमों के बीच संबंध है।

जापानी गणित की सांगकी (ज्यामितीय पहेलियाँ) में फोर्ड वृत्त भी दिखाई देते हैं। विशिष्ट समस्या, जिसे गुंमा प्रान्त में 1824 टैबलेट पर प्रस्तुत किया गया है, सामान्य स्पर्शरेखा के साथ तीन स्पर्श करने वाले वृत्तों के संबंध को कवर करती है। दो बाहरी बड़े वृत्तों के आकार को देखते हुए, उनके बीच के छोटे वृत्त का आकार क्या है? उत्तर फोर्ड वृत्त के बराबर है:

${\frac {1}{\sqrt {r_{\text{middle}}}}}={\frac {1}{\sqrt {r_{\text{left}}}}}+{\frac {1}{\sqrt {r_{\text{right}}}}}.$

फोर्ड वृत्तों का नाम अमेरिकी गणितज्ञ लेस्टर आर. फोर्ड|लेस्टर आर. फोर्ड, सीनियर के नाम पर रखा गया है, जिन्होंने 1938 में उनके बारे में लिखा था।

गुण

1 से 9 तक n के लिए वृत्ताकार चापों के साथ फोर्ड वृत्तों और फेरी आरेख की तुलना। ध्यान दें कि प्रत्येक चाप अपने संगत वृत्तों को समकोण पर प्रतिच्छेद करता है। में the SVG image,[[Category: Templates Vigyan Ready]] इसे और इसकी शर्तों को हाइलाइट करने के लिए किसी वृत्त या वक्र पर होवर करें।

अंश के साथ जुड़े फोर्ड सर्कल $p/q$ द्वारा निरूपित किया जाता है $C[p/q]$ या $C[p,q].$ प्रत्येक परिमेय संख्या के साथ एक Ford वृत्त जुड़ा होता है। इसके अलावा रेखा $y=1$ फोर्ड सर्कल के रूप में गिना जाता है - इसे अनंत से जुड़े फोर्ड सर्कल के रूप में माना जा सकता है, जो कि मामला है $p=1,q=0.$

दो अलग-अलग फोर्ड सर्किल या तो अलग सेट हैं या एक दूसरे से स्पर्शरेखा हैं। फोर्ड सर्किल के कोई भी दो अंदरूनी हिस्से एक दूसरे को नहीं काटते हैं, भले ही कार्टेसियन समन्वय प्रणाली के लिए एक फोर्ड सर्कल स्पर्शरेखा है। परिमेय संख्या निर्देशांक के साथ प्रत्येक बिंदु पर एक्स-अक्ष। अगर $p/q$ 0 और 1 के बीच है, फोर्ड सर्कल जो स्पर्शरेखा हैं $C[p/q]$ के रूप में विभिन्न प्रकार से वर्णित किया जा सकता है

1. मंडलियां $C[r/s]$ कहाँ $|ps-qr|=1,$# भिन्नों से जुड़े वृत्त $r/s$ कि के पड़ोसी हैं $p/q$ कुछ फेरी क्रम में,या
2. मंडलियां $C[r/s]$ कहाँ $r/s$ का अगला बड़ा या अगला छोटा पूर्वज है $p/q$ स्टर्न-ब्रोकॉट के पेड़ में या जहां $p/q$ का अगला बड़ा या अगला छोटा पूर्वज है $r/s$.

अगर $C[p/q]$ और $C[r/s]$ दो स्पर्शरेखा Ford वृत्त हैं, फिर वृत्त के माध्यम से $(p/q,0)$ और $(r/s,0)$ (Ford हलकों के केंद्रों का x-निर्देशांक) और वह लंबवत है $x$-अक्ष (जिसका केंद्र x-अक्ष पर है) भी उस बिंदु से होकर गुजरता है जहां दो वृत्त एक दूसरे को स्पर्श करते हैं।

फोर्ड सर्किल को जटिल विमान में घटता के रूप में भी सोचा जा सकता है। जटिल विमान के परिवर्तनों का मॉड्यूलर समूह गामा फोर्ड सर्कल को अन्य फोर्ड सर्कल में मैप करता है।

फोर्ड सर्किल लाइनों द्वारा उत्पन्न अपोलोनियन गैसकेट में हलकों का एक उप-समूह है $y=0$ और $y=1$ और घेरा $C[0/1].$ हाइपरबोलिक ज्योमेट्री (पॉइनकेयर हाफ-प्लेन मॉडल) के मॉडल के रूप में कॉम्प्लेक्स प्लेन के ऊपरी आधे हिस्से की व्याख्या करके, फोर्ड सर्कल को होरोसाइकल के रूप में व्याख्या किया जा सकता है। अतिशयोक्तिपूर्ण ज्यामिति में कोई भी दो कुंडली सर्वांगसमता (ज्यामिति) होती हैं। जब ये होरोसाइकल एपिरोगोन्स द्वारा स्पर्शरेखा बहुभुज होते हैं, तो वे अतिपरवलयिक तल को क्रम-3 एपिरोगोनल टाइलिंग के साथ जोड़ते हैं।

फोर्ड सर्कल का कुल क्षेत्रफल

फोर्ड सर्कल के क्षेत्र के बीच एक कड़ी है, यूलर का कुल कार्य $\varphi ,$ रीमैन जीटा समारोह $\zeta ,$ और एपेरी स्थिरांक $\zeta (3).$ चूंकि कोई भी दो फोर्ड सर्किल प्रतिच्छेद नहीं करते हैं, यह तुरंत फोर्ड सर्किलों के कुल क्षेत्रफल का अनुसरण करता है

$\left\{C[p,q]:0<{\frac {p}{q}}\leq 1\right\}$

1 से कम है। वास्तव में इन फोर्ड सर्किलों का कुल क्षेत्रफल अभिसरण योग द्वारा दिया जाता है, जिसका मूल्यांकन किया जा सकता है। परिभाषा से, क्षेत्र है

$A=\sum _{q\geq 1}\sum _{(p,q)=1 \atop 1\leq p<q}\pi \left({\frac {1}{2q^{2}}}\right)^{2}.$

इस अभिव्यक्ति को सरल बनाना देता है

$A={\frac {\pi }{4}}\sum _{q\geq 1}{\frac {1}{q^{4}}}\sum _{(p,q)=1 \atop 1\leq p<q}1={\frac {\pi }{4}}\sum _{q\geq 1}{\frac {\varphi (q)}{q^{4}}}={\frac {\pi }{4}}{\frac {\zeta (3)}{\zeta (4)}},$

जहां अंतिम समानता यूलर के कुल कार्य के लिए डिरिचलेट जनरेटिंग फंक्शन को दर्शाती है $\varphi (q).$ तब से $\zeta (4)=\pi ^{4}/90,$ यह अंत में बन जाता है

$A={\frac {45}{2}}{\frac {\zeta (3)}{\pi ^{3}}}\approx 0.872284041.$

ध्यान दें कि परिपाटी के मामले में, पिछली गणनाओं में त्रिज्या के वृत्त को शामिल नहीं किया गया था ${\frac {1}{2}}$ अंश के अनुरूप ${\frac {0}{1}}$. इसमें के लिए पूरा सर्कल शामिल है ${\frac {1}{1}}$, जिनमें से आधा इकाई अंतराल के बाहर है, इसलिए योग अभी भी फोर्ड सर्कल द्वारा कवर किए गए इकाई वर्ग का अंश है।

फोर्ड क्षेत्रों (3 डी)

फोर्ड जटिल डोमेन के ऊपर स्थित है

फोर्ड मंडलों की अवधारणा को परिमेय संख्याओं से गॉसियन परिमेय तक सामान्यीकृत किया जा सकता है, फोर्ड क्षेत्रों को दे रहा है। इस निर्माण में, जटिल संख्याएं त्रि-आयामी यूक्लिडियन अंतरिक्ष में एक विमान के रूप में एम्बेडेड होती हैं, और इस विमान में प्रत्येक गॉसियन तर्कसंगत बिंदु के लिए उस बिंदु पर विमान के लिए एक गोलाकार स्पर्शरेखा का निर्माण होता है। गॉसियन तर्कसंगत के लिए सबसे कम शब्दों में प्रतिनिधित्व किया गया $p/q$, इस गोले का व्यास होना चाहिए $1/2q{\bar {q}}$ कहाँ ${\bar {q}}$ के जटिल संयुग्म का प्रतिनिधित्व करता है $q$. परिणामी गोले गॉसियन परिमेय के जोड़े के लिए स्पर्शरेखा हैं $P/Q$ और $p/q$ साथ $|Pq-pQ|=1$, और अन्यथा वे एक दूसरे को प्रतिच्छेद नहीं करते।

यह भी देखें

• अपोलोनियन गैस्केट - एक लाइन के बजाय एक सर्कल में अनंत पारस्परिक रूप से स्पर्शरेखा वाले वृत्तों वाला एक फ्रैक्टल
• स्टेनर चेन
• पप्पस चेन

बाहरी संबंध

• Ford's Touching Circles at cut-the-knot
• Weisstein, Eric W. "Ford Circle". MathWorld.
• Bonahon, Francis. "Funny Fractions and Ford Circles" (YouTube video). Brady Haran. Archived from the original on 2021-12-21. Retrieved 9 June 2015.