बूटस्ट्रैप संग्रहण

बूटस्ट्रैप एकत्रीकरण, जिसे बैगिंग (बूटस्ट्रैप एकत्रीकरण से) भी कहा जाता है, एक मेटा-एल्गोरिथ्म का एकत्रीकरण है जिसे स्थिरता (सीखने का सिद्धांत) और सांख्यिकीय वर्गीकरण और प्रतिगमन विश्लेषण में उपयोग किए जाने वाले यंत्र अधिगम एल्गोरिदम की सटीकता में सुधार करने के लिए डिज़ाइन किया गया है। यह विचरण को भी कम करता है और अतिउपयुक्त से बचने में मदद करता है। यद्यपि यह प्रायः निर्णय वृक्ष सीखने के विधियों पर क्रियान्वित होता है, परन्तु इसका उपयोग किसी भी प्रकार की विधि के साथ किया जा सकता है। बैगिंग मॉडल औसत दृष्टिकोण का एक विशेष घटना है।

यांत्रिकी का विवरण

एक मानक प्रशिक्षण सेट दिया $D$ आकार n का, बैगिंग m नए प्रशिक्षण सेट $D_{i}$ उत्पन्न करता है , प्रत्येक आकार n', 𝐷 संभावना वितरण से नमूनाकरण (सांख्यिकी) द्वारा परिमित समर्थन और नमूनाकरण (सांख्यिकी) के साथ चयनित इकाइयों का प्रतिस्थापन के साथ प्रतिचयन द्वारा, प्रत्येक $D_{i}$ में कुछ प्रेक्षणों को दोहराया जा सकता है यदि n′=n, तो बड़े n सेट के लिए $D_{i}$, 𝐷 के अनूठे उदाहरणों का अंश (1 - 1/e (गणितीय स्थिरांक)) (≈63.2%) होने की आशा है, अतिरिक्त डुप्लिकेट हैं। इस तरह के नमूने को बूटस्ट्रैप (सांख्यिकी) नमूने के रूप में जाना जाता है। प्रतिस्थापन के साथ नमूनाकरण सुनिश्चित करता है कि प्रत्येक बूटस्ट्रैप अपने साथियों से स्वतंत्र है, क्योंकि यह नमूनाकरण करते समय पिछले चुने हुए नमूनों पर निर्भर नहीं करता है। दोबारा, एम मॉडल को उपरोक्त एम बूटस्ट्रैप नमूनों का उपयोग करके उपयुक्त किया जाता है और आउटपुट (प्रतिगमन के लिए) या वोटिंग (वर्गीकरण के लिए) के औसत से जोड़ा जाता है।

बूटस्ट्रैप एकत्रीकरण की अवधारणा के लिए एक उदाहरण

बैगिंग से अस्थिर प्रक्रियाओं में सुधार होता है, जिसमें सम्मिलित हैं, उदाहरण के लिए, कृत्रिम तंत्रिका नेटवर्क, वर्गीकरण और प्रतिगमन वृक्ष, और रैखिक प्रतिगमन में सबसेट चयनबैगिंग को प्रीइमेज लर्निंग को अपेक्षाकृत अच्छा बनाने के लिए दिखाया गया था। दूसरी ओर, यह के-निकटतम पड़ोसियों जैसे स्थिर विधियों के प्रदर्शन को हल्का कर सकता है।

एल्गोरिथ्म की प्रक्रिया

मुख्य उपबंध

बूटस्ट्रैप एकत्रीकरण में तीन प्रकार के आंकड़े तय करने होते हैं। ये मूल, बूटस्ट्रैप और आउट-ऑफ़-बैग आंकड़े तय करने हैं। नीचे दिए गए प्रत्येक अनुभाग में बताया जाएगा कि मूल आंकड़े तय करने को छोड़कर प्रत्येक आंकड़े तय करने कैसे बनाया जाता है। जो भी जानकारी दी जाती है वह मूल आंकड़े तय करने होता है।

बूटस्ट्रैप आंकड़े तय करने बनाना

बूटस्ट्रैप आंकड़े तय करने मूल आंकड़े तय करने से अव्यवस्थित तरीके से वस्तुओं को चुनकर बनाया जाता है। साथ ही, यह मूल आंकड़े तय करने के समान आकार का होना चाहिए। यद्यपि, अंतर यह है कि बूटस्ट्रैप आंकड़े तय करने में डुप्लिकेट ऑब्जेक्ट हो सकते हैं। यह प्रदर्शित करने के लिए सरल उदाहरण है कि यह नीचे दिए गए चित्रण के साथ कैसे काम करता है:

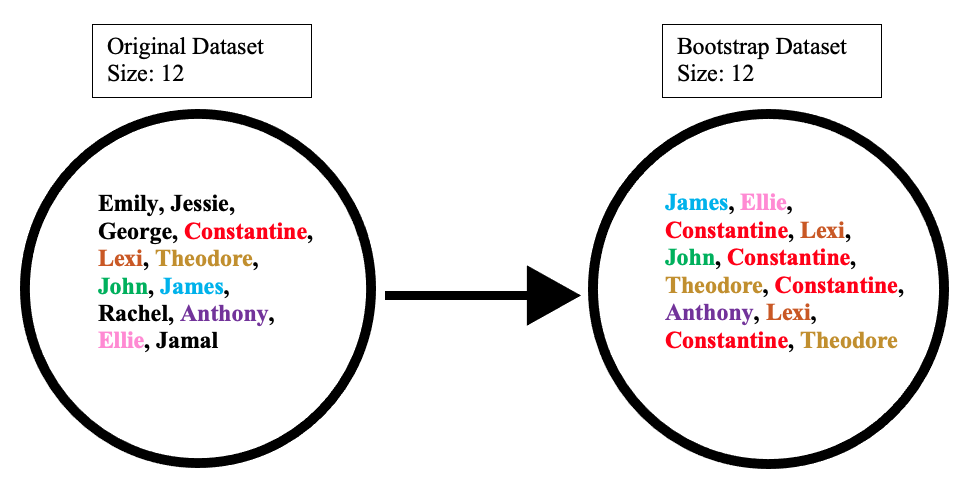मान लीजिए कि मूल आंकड़े तय करने 12 लोगों का समूह है। ये लोग हैं एमिली, जेसी, जॉर्ज, कॉन्स्टेंटाइन, लेक्सी, थियोडोर, जॉन, जेम्स, राहेल, एंथोनी, ऐली और जमाल।

अव्यवस्थित तरीके से नामों का एक समूह चुनकर, हम कहते हैं कि हमारे बूटस्ट्रैप आंकड़े तय करने में जेम्स, ऐली, कॉन्सटेंटाइन, लेक्सी, जॉन, कॉन्सटेंटाइन, थियोडोर, कॉन्सटेंटाइन, एंथोनी, लेक्सी, कॉन्स्टेंटाइन और थियोडोर थे। इस घटना में, बूटस्ट्रैप नमूने में कॉन्स्टेंटाइन के लिए चार डुप्लिकेट और लेक्सी और थियोडोर के लिए दो डुप्लिकेट सम्मिलित थे।

आउट-ऑफ-बैग आंकड़े तय करने बनाना

आउट-ऑफ़-बैग आंकड़े तय करने उन शेष लोगों का प्रतिनिधित्व करता है जो बूटस्ट्रैप आंकड़े तय करने में नहीं थे। इसकी गणना मूल और बूटस्ट्रैप आंकड़े तय करने के बीच के अंतर को लेकर की जा सकती है। इस घटना में, शेष नमूने जिनका चयन नहीं किया गया था वे एमिली, जेसी, जॉर्ज, राहेल और जमाल हैं। ध्यान रखें कि चूंकि दोनों आंकड़े तय करने हैं, अंतर लेते समय बूटस्ट्रैप आंकड़े तय करने में डुप्लिकेट नामों को अनदेखा कर दिया जाता है। नीचे दिया गया उदाहरण दिखाता है कि गणित कैसे किया जाता है:

महत्व

बूटस्ट्रैप और आउट-ऑफ़-बैग आंकड़े तय करने बनाना महत्वपूर्ण है क्योंकि इसका उपयोग अनियमित जंगल एल्गोरिथम की सटीकता का परीक्षण करने के लिए किया जाता है। उदाहरण के लिए, एक मॉडल जो बूटस्ट्रैप/आउट-ऑफ-बैग आंकड़े तय करने का उपयोग करके 50 वृक्षों का उत्पादन करता है, उसके पास 10 वृक्ष बनाने की तुलना में अपेक्षाकृत अच्छी सटीकता होगी। चूंकि एल्गोरिदम कई वृक्ष उत्पन्न करता है और इसलिए कई आंकड़े तय करने बूटस्ट्रैप आंकड़े तय करने से किसी ऑब्जेक्ट को छोड़ने का अवसर कम होता है। अगले कुछ खंड इस बारे में बात करते हैं कि कैसे अनियमित जंगल एल्गोरिथम अधिक विस्तार से काम करता है।

निर्णय वृक्ष का निर्माण

एल्गोरिथम के अगले चरण में बूटस्ट्रैप किए गए आंकड़े तय करने से निर्णय वृक्ष बनाना सम्मिलित है। इसे प्राप्त करने के लिए, प्रक्रिया प्रत्येक जीन/विशेषता की जांच करती है और यह निर्धारित करती है कि विशेषता की उपस्थिति या अनुपस्थिति के कितने नमूने सकारात्मक या नकारात्मक परिणाम देते हैं। इस जानकारी का उपयोग तब भ्रम मैट्रिक्स की गणना करने के लिए किया जाता है, जो क्लासिफायर के रूप में उपयोग किए जाने पर वास्तविक सकारात्मक, झूठी सकारात्मक, वास्तविक नकारात्मक और सुविधा के झूठे नकारात्मक को सूचीबद्ध करता है। इन सुविधाओं को दोबारा उनके भ्रम मैट्रिक्स के आधार पर विभिन्न निर्णय वृक्ष सीखने के अनुसार क्रमबद्ध किया जाता है। कुछ सामान्य मेट्रिक्स में सकारात्मक शुद्धता का अनुमान (वास्तविक सकारात्मक से झूठी सकारात्मक घटाकर गणना), अच्छाई का माप और निर्णय वृक्षों में सूचना लाभ सम्मिलित हैं। दोबारा इन सुविधाओं का उपयोग नमूनों को दो सेटों में विभाजित करने के लिए किया जाता है: वे जिनके पास शीर्ष विशेषता है, और जिनके पास नहीं है।

नीचे दिया गया चित्र आंकड़े को वर्गीकृत करने के लिए उपयोग की जाने वाली गहराई दो के एक निर्णय वृक्ष को दर्शाता है। उदाहरण के लिए, एक आंकड़े पॉइंट जो विशेषता 1 को प्रदर्शित करता है, परन्तु विशेषता 2 को नहीं, उसे नंबर दिया जाएगा। एक और बिंदु जो विशेषता 1 को प्रदर्शित नहीं करता है, परन्तु विशेषता 3 को प्रदर्शित करता है, उसे हाँ दिया जाएगा।

वांछित गहराई तक पहुंचने तक वृक्ष के क्रमिक स्तरों के लिए इस प्रक्रिया को पुनरावर्ती रूप से दोहराया जाता है। वृक्ष के बिल्कुल नीचे, जो नमूने अंतिम विशेषता के लिए सकारात्मक परीक्षण करते हैं, उन्हें प्रायः सकारात्मक के रूप में वर्गीकृत किया जाता है, जबकि जिन लोगों में विशेषता की कमी होती है उन्हें नकारात्मक के रूप में वर्गीकृत किया जाता है। दोबारा इन वृक्षों को नए आंकड़े को वर्गीकृत करने के लिए भविष्यवाणियों के रूप में उपयोग किया जाता है।

यादृच्छिक वन

एल्गोरिथम के अगले भाग में बूटस्ट्रैप्ड वृक्षों के बीच परिवर्तनशीलता के एक और तत्व को सम्मिलित करना है। प्रत्येक वृक्ष के अलावा केवल नमूनों के बूटस्ट्रैप किए गए सेट की जांच करते हुए, क्लासिफायर के रूप में रैंकिंग करते समय केवल एक छोटी परन्तु लगातार अनूठी विशेषताओं पर विचार किया जाता है। इसका अर्थ यह है कि प्रत्येक वृक्ष केवल एक छोटी स्थिर संख्या से संबंधित आंकड़े के बारे में जानता है, और नमूनों की एक चर संख्या जो मूल आंकड़े तय करने से कम या उसके बराबर है। नतीजतन, वृक्ष अधिक विविध ज्ञान से प्राप्त उत्तरों की एक विस्तृत श्रृंखला वापस करने की अधिक संभावना रखते हैं। इसका परिणाम एक यादृच्छिक वन में होता है, जिसमें यादृच्छिकता के बिना उत्पन्न एकल निर्णय वृक्ष पर कई लाभ होते हैं। एक यादृच्छिक जंगल में, प्रत्येक वृक्ष अपनी विशेषताओं के आधार पर नमूने को सकारात्मक के रूप में वर्गीकृत करने या न करने के लिए मतदान करता है। नमूना तब बहुमत वोट के आधार पर वर्गीकृत किया जाता है। इसका एक उदाहरण नीचे दिए गए आरेख में दिया गया है, जहां एक यादृच्छिक वन में चार वृक्ष म्यूटेशन ए, बी, एफ और जी वाले रोगी को कैंसर है या नहीं, इस पर मतदान करते हैं। क्योंकि चार में से तीन वृक्ष हाँ कहते हैं, तब रोगी को कैंसर पॉजिटिव के रूप में वर्गीकृत किया जाता है।

उनके गुणों के कारण, यादृच्छिक जंगलों को सबसे सटीक खुदाई एल्गोरिदम आंकड़ेमें से एक माना जाता है, उनके आंकड़े को अतिउपयुक्त करने की संभावना कम होती है, और बड़े आंकड़े तय करने के लिए भी जल्दी और कुशलता से चलते हैं। प्रतिगमन विश्लेषण के विपरीत वे वर्गीकरण के लिए मुख्य रूप से उपयोगी होते हैं, जो आंकड़े तय करने में सांख्यिकीय चर के बीच देखे गए कनेक्शन को आकर्षित करने का प्रयास करता है। यह बैंकिंग, स्वास्थ्य सेवा, शेयर बाजार और ई-कॉमर्स जैसे क्षेत्रों में यादृच्छिक वनों को विशेष रूप से उपयोगी बनाता है जहां पिछले आंकड़े के आधार पर भविष्य के परिणामों की भविष्यवाणी करने में सक्षम होना महत्वपूर्ण है। उनके अनुप्रयोगों में से एक आनुवंशिक कारकों के आधार पर कैंसर की भविष्यवाणी करने के लिए एक उपयोगी उपकरण के रूप में होगा, जैसा कि उपरोक्त उदाहरण में देखा गया है।

यादृच्छिक वन डिजाइन करते समय विचार करने के लिए कई महत्वपूर्ण कारक हैं। यदि यादृच्छिक जंगलों में वृक्ष बहुत गहरे हैं, तो अति-विशिष्टता के कारण अतिउपयुक्त अभी भी हो सकती है। यदि जंगल बहुत बड़ा है, तो एल्गोरिथम बढ़े हुए क्रम के कारण कम कुशल हो सकता है। अनियमित जंगल भी प्रायः तब अच्छा प्रदर्शन नहीं करते हैं जब थोड़ी परिवर्तनशीलता के साथ विरल आंकड़े दिया जाता है।यद्यपि , उनके पास समान आंकड़े वर्गीकरण एल्गोरिदम जैसे तंत्रिका नेटवर्क पर अभी भी कई लाभ हैं, क्योंकि वे व्याख्या करने में बहुत आसान हैं और प्रायः प्रशिक्षण के लिए कम आंकड़े की आवश्यकता होती है। यादृच्छिक वनों के एक अभिन्न अंग के रूप में, बूटस्ट्रैप एकत्रीकरण वर्गीकरण एल्गोरिदम के लिए बहुत महत्वपूर्ण है, और परिवर्तनशीलता का एक महत्वपूर्ण तत्व प्रदान करता है जो नए आंकड़े का विश्लेषण करते समय बढ़ी हुई सटीकता की अनुमति देता है, जैसा कि नीचे चर्चा की गई है।

अनियमित जंगल में सुधार और बैगिंग

जबकि ऊपर वर्णित यांत्रिकीें यादृच्छिक वनों और बूटस्ट्रैपिंग (अन्यथा बूटस्ट्रैपिंग के रूप में जानी जाती हैं) का उपयोग करती हैं, कुछ यांत्रिकीें हैं जिनका उपयोग उनके निष्पादन और मतदान के समय, उनकी भविष्यवाणी सटीकता और उनके समग्र प्रदर्शन को अपेक्षाकृत अच्छा बनाने के लिए किया जा सकता है। एक कुशल यादृच्छिक वन बनाने के लिए निम्नलिखित महत्वपूर्ण कदम हैं:

1. वृक्षों की अधिकतम गहराई निर्दिष्ट करें: अपने यादृच्छिक वन को तब तक प्रचलन में रखने की अनुमति न दे जब तक कि सभी नोड्स शुद्ध न हों, अतिउपयुक्त की संभावना को और कम करने के लिए इसे एक निश्चित बिंदु पर काट देना अपेक्षाकृत अच्छा है।
2. आंकड़े तय करने की छँटाई करें: बहुत बड़े आंकड़े तय करने का उपयोग करने से ऐसे परिणाम तैयार हो सकते हैं जो एक छोटे सेट की तुलना में प्रदान किए गए आंकड़े का कम संकेत देते हैं जो अधिक सटीक रूप से दर्शाता है कि किस पर ध्यान केंद्रित किया जा रहा है।
   • केवल मूल बैगिंग प्रक्रिया के अतिरिक्त प्रत्येक नोड विभाजन पर आंकड़े की छंटाई संचालित रखें।
3. सटीकता या गति पर निर्णय लें: वांछित परिणामों के आधार पर, जंगल के भीतर वृक्षों की संख्या बढ़ाना या घटाना मदद कर सकता है। वृक्षों की संख्या बढ़ाने से प्रायः अधिक सटीक परिणाम मिलते हैं जबकि वृक्षों की संख्या कम करने से जल्दी परिणाम मिलते हैं।

रैंडम फ़ॉरेस्ट और बैगिंग के फायदे और नुकसान

फायदे	नुकसान
सामान्यीकरण और स्केलिंग के लिए समग्र रूप से कम आवश्यकताएं सम्मिलित हैं, जिससे यादृच्छिक वनों का उपयोग अधिक सुविधाजनक हो जाता है।	यदि बूटस्ट्रैप किए जा रहे आंकड़े और वनों के भीतर उपयोग किए जाने वाले आंकड़े में थोड़ा सा परिवर्तन होता है, तो एल्गोरिथम महत्वपूर्ण रूप से बदल सकता है। दूसरे शब्दों में, यादृच्छिक वन अविश्वसनीय रूप से अपने आंकड़े सेट पर निर्भर होते हैं, इन्हें बदलने से अलग-अलग पेड़ों की संरचना में भारी बदलाव आ सकता है।
आसान आंकड़े तैयार करना। एक यादृच्छिक वन बनाने के लिए एक बूटस्ट्रैप सेट और एक निश्चित संख्या में निर्णय वृक्ष बनाकर आंकड़े तैयार किये जाता है, जो यादृच्छिक वन सेक्शन में बताए गए विशेषता चयन का भी उपयोग करता है।	अकेले निर्णय पेड़ या अन्य एल्गोरिदम की तुलना में यादृच्छिक वन लागू करने के लिए अधिक जटिल हैं। ऐसा इसलिए है क्योंकि वे बैगिंग के लिए अतिरिक्त कदम उठाते हैं, साथ ही पूरे जंगल का उत्पादन करने के लिए रिकर्सन की आवश्यकता होती है, जो कार्यान्वयन को जटिल बनाता है। इस वजह से, इसे और अधिक कम्प्यूटेशनल शक्ति और कम्प्यूटेशनल संसाधनों की आवश्यकता होती है।
कई निर्णय वृक्षों से मिलकर, वन एकल वृक्षों की तुलना में अधिक सटीक भविष्यवाणी करने में सक्षम हैं।	निर्णय पेड़ों की तुलना में आंकड़े को प्रशिक्षित करने में अधिक समय लगता है। एक बड़ा जंगल होने से उस गति को कम करना आरंभ हो सकता है जिसमें किसी का कार्यक्रम संचालित होता है क्योंकि इसे बहुत अधिक आंकड़े पार करना पड़ता है, भले ही प्रत्येक पेड़ नमूनों और सुविधाओं के एक छोटे सेट का उपयोग कर रहा हो।
गैर रेखीय आंकड़े के साथ अच्छी तरह से काम करता है। जैसा कि अधिकांश वृक्ष आधारित एल्गोरिदम रैखिक विभाजन का उपयोग करते हैं, पेड़ों के एक समूह का उपयोग आंकड़े पर एक पेड़ का उपयोग करने से बेहतर काम करता है जिसमें गैर-रैखिक गुण होते हैं (अर्थात अधिकांश वास्तविक विश्व वितरण)। गैर-रैखिक आंकड़े के साथ अच्छी तरह से काम करना एक बड़ा लाभ है क्योंकि अन्य आंकड़े खनन यांत्रिकी जैसे सिंगल निर्णय वृक्ष इसे भी सँभालना नहीं करते हैं।	यादृच्छिक वन की तुलना में व्याख्या करना बहुत आसान है। एक अकेले पेड़ को हाथ से (एक मानव द्वारा) चलाया जा सकता है, जिससे पेड़ वास्तव में क्या कर रहा है, इसके विश्लेषक के लिए कुछ हद तक "समझाने योग्य" समझ पैदा होती है। जैसे-जैसे पेड़ों की संख्या बढ़ती है और उन पेड़ों को भविष्यवाणियों में सम्मिलित करने के लिए योजनाएँ बढ़ती हैं, यह समीक्षा असंभव नहीं तो और अधिक कठिन हो जाती है।
ओवरफिटिंग का संकट कम होता है और बड़े आंकड़े सेट पर भी कुशलता से चलता है। यह यादृच्छिक सुविधा चयन के साथ-साथ बैगिंग के यादृच्छिक वन के उपयोग का परिणाम है।	प्रशिक्षण आंकड़े की सीमा से परे भविष्यवाणी नहीं करता। यह एक चोर है क्योंकि बैगिंग अक्सर प्रभावी होती है, सभी आंकड़े पर विचार नहीं किया जा रहा है, इसलिए यह संपूर्ण आंकड़ेसेट की भविष्यवाणी नहीं कर सकता है।
यादृच्छिक वन वर्गीकारक उच्च सटीकता और गति के साथ काम करता है। छोटे आंकड़े सेट का उपयोग करने के कारण यादृच्छिक वन निर्णय पेड़ों की तुलना में बहुत तेज़ होते हैं।	विशिष्ट परिणामों को दोबारा से बनाने के लिए आपको बूटस्ट्रैप सेट उत्पन्न करने के लिए उपयोग किए जाने वाले सटीक यादृच्छिक बीज का ट्रैक रखने की आवश्यकता है। अनुसंधान के लिए या आंकड़े खनन क्लास के भीतर आंकड़े एकत्र करते समय यह महत्वपूर्ण हो सकता है। यादृच्छिक जंगलों के लिए यादृच्छिक बीजों का उपयोग करना आवश्यक है, लेकिन यदि बीजों को अभिलेख करने में विफलता हो तो वनों पर आधारित अपने चार्चाओ का समर्थन करना कठिन हो सकता है।
कई आउटलेयर के साथ लापता आंकड़े और आंकड़ेसेट के साथ अच्छी तरह से डील करता है। वे इससे निपटने के लिए बिनिंग का उपयोग करते हैं, या उन मूल्यों से बचने के लिए मूल्यों को एक साथ समूहित करते हैं जो बहुत दूर हैं।

एल्गोरिथम (वर्गीकरण)

वर्गीकरण के लिए उपयोग किए जाने पर बैगिंग एल्गोरिथम का फ़्लो चार्ट

वर्गीकरण के लिए, एक प्रशिक्षण सेट का उपयोग करें $D$, प्रेरक $I$ और बूटस्ट्रैप नमूनों की संख्या $m$ इनपुट के रूप में। एक वर्गीकारक उत्पन्न करें $C^{*}$ आउटपुट के रूप में

1. बनाएं $m$ नए प्रशिक्षण सेट $D_{i}$, से $D$ प्रतिस्थापन के साथ
2. वर्गीकारक $C_{i}$ प्रत्येक सेट से बनाया गया है $D_{i}$ का उपयोग करते हुए $I$ सेट का वर्गीकरण निर्धारित करने के लिए $D_{i}$
3. अंत में वर्गीकारक $C^{*}$ क्लासिफायर के पहले बनाए गए सेट का उपयोग करके उत्पन्न होता है $C_{i}$ मूल आंकड़े सेट पर $D$, उप-वर्गीकरणकर्ताओं द्वारा अक्सर वर्गीकरण की भविष्यवाणी की जाती है $C_{i}$ अंतिम वर्गीकरण है

$I$ के लिए = 1 से m {

 D' = D से बूटस्ट्रैप नमूना (प्रतिस्थापन के साथ नमूना) 
 Ci = I(D')

} C*(x) = argmax #{i:Ci(x)=y} (अक्सर पूर्वानुमानित लेबल y)

 वाई∈वाई 

उदाहरण: ओजोन आंकड़े

बैगिंग के बुनियादी सिद्धांतों को स्पष्ट करने के लिए, नीचे ओजोन और तापमान के बीच संबंधों पर एक विश्लेषण है (पीटर रूसो और लेरॉय से आंकड़े) (1986), आर (प्रोग्रामिंग लैंग्वेज) में किया गया विश्लेषण)।

स्कैटर प्लॉट के आधार पर, इस आंकड़े सेट में तापमान और ओजोन के बीच संबंध अरैखिक प्रतीत होता है। गणितीय रूप से इस संबंध का वर्णन करने के लिए, स्थानीय प्रतिगमन स्मूथर्स (बैंडविड्थ 0.5 के साथ) का उपयोग किया जाता है। संपूर्ण आंकड़े सेट के लिए एक आसान बनाने के अतिरिक्त , 100 बूटस्ट्रैप (सांख्यिकी) नमूने तैयार किए गए थे। प्रत्येक नमूना मूल आंकड़े के एक यादृच्छिक सबसेट से बना होता है और मास्टर सेट के वितरण और परिवर्तनशीलता की अवस्था रखता है। प्रत्येक बूटस्ट्रैप नमूने के लिए, एक एलओईएसएस स्मूथ उपयुक्त था। इन 100 स्मूथर्स से भविष्यवाणियां तब आंकड़े की सीमा में की गईं। काली रेखाएँ इन प्रारंभिक भविष्यवाणियों का प्रतिनिधित्व करती हैं। पंक्तियों में उनकी भविष्यवाणियों में सहमति की कमी होती है और वे अपने आंकड़े बिंदुओं से लाइनों के लड़खड़ाते प्रवाह को अतिउपयुक्त स्पष्ट करते हैं।

[[iदाना: ओजोन.पीएनजी|केंद्र मूल आंकड़े सेट के एक सबसेट के अनुरूप प्रत्येक 100 स्मूथर्स का औसत लेकर, हम एक बैगेड भविष्यवक्ता (लाल रेखा) पर पहुंचते हैं। लाल रेखा का प्रवाह स्थिर है और किसी भी आंकड़े बिंदु(ओं) के अनुरूप नहीं है।

लाभ और नुकसान

लाभ:

• कई कमजोर शिक्षार्थी समग्र रूप से पूरे सेट में एक ही शिक्षार्थी से अपेक्षाकृत अच्छा प्रदर्शन करते हैं, और कम अतिउपयुक्त होते हैं
• उच्च-विचरण पूर्वाग्रह (सांख्यिकी) में विचरण को हटाता है। (कम-पूर्वाग्रह कमजोर शिक्षार्थी)
• समानांतर कंप्यूटिंग में प्रदर्शन किया जा सकता है, क्योंकि संयोजन से पहले प्रत्येक अलग बूटस्ट्रैप को अपने आप संसाधित किया जा सकता है

नुकसान:

• उच्च पूर्वाग्रह वाले कमजोर शिक्षार्थियों के लिए, बैगिंग भी उच्च पूर्वाग्रह को अपने कुल योग में ले जाएगा।
• आंकड़े सेट के आधार पर कम्प्यूटेशनल रूप से अधिक मूल्य हो सकता है

इतिहास

बूटस्ट्रैप एकत्रीकरण की अवधारणा बूटस्ट्रैपिंग की अवधारणा से ली गई है जिसे ब्रैडली एफ्रॉन द्वारा विकसित किया गया था।बूटस्ट्रैप एकत्रीकरण लियो ब्रिमन द्वारा प्रस्तावित किया गया था जिन्होंने संक्षिप्त शब्द बैगिंग (बूटस्ट्रैप एकत्रीकरण) भी गढ़ा था। ब्रिमन ने अव्यवस्थित तरीके से उत्पन्न प्रशिक्षण सेटों के वर्गीकरण के संयोजन से वर्गीकरण में सुधार करने के लिए 1994 में बैगिंग की अवधारणा विकसित की। उन्होंने तर्क दिया, यदि सीखने के सेट को परेशान करने से भविष्यवाणियों में महत्वपूर्ण परिवर्तन हो सकते हैं, तो बैगिंग सटीकता में सुधार कर सकती है।

यह भी देखें

• बूस्टिंग (मेटा-एल्गोरिदम)
• बूटस्ट्रैपिंग (सांख्यिकी)
• क्रॉस-वैलिडेशन (सांख्यिकी)
• आउट-ऑफ-बैग त्रुटि
• अव्यवस्थित जंगल
• अनियमित सबस्पेस विधि (विशेषता बैगिंग)
• कुशल फ्रंटियर को दोबारा से तैयार किया
• भविष्यवाणी विश्लेषण | भविष्य कहनेवाला विश्लेषण: वर्गीकरण और प्रतिगमन वृक्ष

अग्रिम पठन

• ब्रिमन, लियो (1996)। "बैगिंग भविष्यवक्ता"। यंत्र अधिगम। 24 (2): 123-140। साइटसीरएक्स 10.1.1.32.9399। डीओआई: 10.1007/बीएफ00058655। एस2सीआईडी 47328136.
• अल्फारो, ई., गेमेज़, एम. और गार्सिया, एन. (2012)। "अदाबाग: ऐडाबूस्ट। एम1, ऐडाबूस्ट-एसएएमएमई और बैगिंग के साथ वर्गीकरण के लिए एक आर पैकेज"। Template:जर्नल उद्धृत करें: जर्नल की आवश्यकता का हवाला दें |जर्नल= (सहायता)
• कोत्सियंटिस, सॉटिरिस (2014)। "वर्गीकरण समस्याओं से निपटने के लिए बैगिंग और बूस्टिंग वेरिएंट: एक सर्वेक्षण"। ज्ञान अभियांत्रिकी। समीक्षा। 29 (1): 78-100। डीओआई:10.1017/S0269888913000313. एस2सीआईडी 27301684.
• बोहेमके, ब्राडली; ग्रीनवेल, ब्रैंडन (2019)। "बैगिंग"। आर. चैपमैन एंड हॉल के साथ हैंड्स-ऑन मशीन लर्निंग। पीपी। 191-202। आईएसबीएन 978-1-138-49568-5।