प्राथमिक प्रवाह

नेवियर-स्टोक्स समीकरणों के बड़े संदर्भ में लेकिन विशेष रूप से संभावित सिद्धांत के संदर्भ में प्राथमिक प्रवाह बुनियादी प्रवाह का एक संग्रह है जिससे विभिन्न तकनीकों के साथ अधिक जटिल प्रवाह का निर्माण संभव है। इस लेख में ऐतिहासिक कारणों से शब्द प्रवाह का उपयोग शब्द समाधान के लिए एक दूसरे के स्थान पर किया जाता है।

अधिक जटिल समाधान बनाने के लिए शामिल तकनीकें हो सकती हैं उदाहरण के लिए सुपरपोज़िशन सिद्धांत द्वारा, टोपोलॉजी जैसी तकनीकों द्वारा या उन्हें एक निश्चित पड़ोस, उपडोमेन या सीमा परत पर स्थानीय समाधान के रूप में माना जाता है और एक साथ पैच किया जाता है। प्राथमिक प्रवाह को नेवियर-स्टोक्स से प्राप्त विभिन्न प्रकार के समीकरणों के बुनियादी निर्माण खंड (मौलिक समाधान, स्थानीय समाधान और solitons) माना जा सकता है। कुछ प्रवाह विशिष्ट मामलों की बाधाओं को दर्शाते हैं जैसे कि असंगत प्रवाह या इर्रोटेशनल प्रवाह प्रवाह, या दोनों, जैसा कि संभावित प्रवाह के मामले में होता है, और कुछ प्रवाह अक्सर 2 आयामों के मामले में सीमित होते हैं। द्रव गतिकी से सभी क्षेत्र सिद्धांत (भौतिकी) के संबंध के कारण यह समझना महत्वपूर्ण है कि कैसे ये सभी प्रवाह न केवल वायुगतिकी बल्कि सामान्य रूप से सभी क्षेत्र सिद्धांत (भौतिकी) के लिए प्रासंगिक हैं। इसे परिप्रेक्ष्य में रखने के लिए सीमा परतों को जेनेरिक कई गुना पर टोपोलॉजिकल दोषों के रूप में व्याख्या किया जा सकता है, और द्रव गतिकी उपमाओं और विद्युत चुंबकत्व, क्वांटम यांत्रिकी और सामान्य सापेक्षता में सीमित मामलों पर विचार कर सकते हैं कि ये सभी समाधान सैद्धांतिक भौतिकी में हाल के विकास के मूल में कैसे हैं। जैसे कि विज्ञापन/cft द्वैत, SYK मॉडल, निमैटिक तरल पदार्थों की भौतिकी, दृढ़ता से सहसंबद्ध प्रणालियाँ और यहाँ तक कि क्वार्क ग्लूऑन प्लाज़्मा।

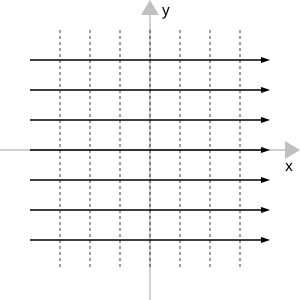
द्वि-आयामी समान प्रवाह

एक आदर्श समान प्रवाह के लिए संभावित प्रवाह स्ट्रीमलाइन, स्ट्रीकलाइन और पाथलाइन

अंतरिक्ष में किसी भी स्थिति में द्रव के एकसमान वेग को देखते हुए:

$\mathbf {V_{0}} =v_{0}\cos(\theta _{0})\mathbf {e} _{x}+v_{0}\sin(\theta _{0})\mathbf {e} _{y}$

यह प्रवाह असम्पीडित है क्योंकि वेग स्थिर है, वेग घटकों का पहला डेरिवेटिव शून्य है, और कुल विचलन शून्य है: $\nabla \cdot \mathbf {v} =0$ सर्कुलेशन (द्रव गतिकी) को देखते हुए हमेशा शून्य होता है, प्रवाह भी इर्रोटेशनल होता है, हम इसे केल्विन के सर्कुलेशन प्रमेय और vorticity की स्पष्ट गणना से प्राप्त कर सकते हैं:

$\omega _{z}={\frac {\partial v_{x}}{\partial y}}-{\frac {\partial v_{y}}{\partial x}}=0$

असम्पीडित और द्वि-आयामी होने के कारण, यह प्रवाह एक धारा समारोह से निर्मित होता है:

$v_{x}={\frac {\partial \psi }{\partial y}}$

$v_{y}=-{\frac {\partial \psi }{\partial x}}$

किस से

$\psi =-v_{0}\sin(\theta _{0})x+v_{0}\cos(\theta _{0})y$

और बेलनाकार निर्देशांक में:

$v_{r}=-{\frac {1}{r}}{\frac {\partial \psi }{\partial \theta }}$

$v_{\theta }={\frac {\partial \psi }{\partial r}}$

किस से

$\psi =-v_{0}r\sin(\theta -\theta _{0})$

हमेशा की तरह स्ट्रीम फ़ंक्शन को एक स्थिर मान तक परिभाषित किया जाता है जिसे हम यहाँ शून्य के रूप में लेते हैं। हम यह भी पुष्टि कर सकते हैं कि प्रवाह इर्रोटेशनल है:

$\nabla ^{2}\psi =0$

अपरिमेय होने के कारण, इसके बजाय संभावित कार्य है:

$v_{x}=-{\frac {\partial \phi }{\partial x}}$

$v_{y}=-{\frac {\partial \phi }{\partial y}}$

और इसलिए

$\phi =-v_{0}\cos(\theta _{0})x-v_{0}\sin(\theta _{0})y$

और बेलनाकार निर्देशांक में

$v_{r}={\frac {\partial \phi }{\partial r}}$

$v_{\theta }={\frac {1}{r}}{\frac {\partial \phi }{\partial \theta }}$

$\phi =-v_{0}r\cos(\theta -\theta _{0})$

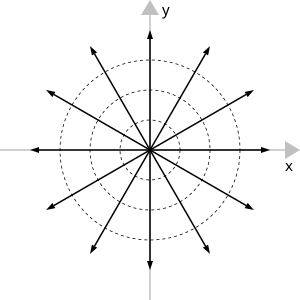
द्वि-आयामी रेखा स्रोत

पोटेंशियल फ्लो एक आदर्श लाइन सोर्स के लिए स्ट्रीमलाइन, स्ट्रीकलाइन और पाथलाइन

एक निश्चित दर पर उत्सर्जक एक लंबवत रेखा का मामला द्रव क्यू प्रति इकाई लंबाई की एक निरंतर मात्रा एक रेखा स्रोत है। समस्या में एक बेलनाकार समरूपता है और ऑर्थोगोनल तल पर दो आयामों में इसका इलाज किया जा सकता है।

लाइन स्रोत और लाइन सिंक (नीचे) महत्वपूर्ण प्रारंभिक प्रवाह हैं क्योंकि वे असम्पीडित तरल पदार्थों के लिए मोनोपोल (ओं) की भूमिका निभाते हैं (जिन्हें सोलेनोइडल क्षेत्र यानी विचलन मुक्त फ़ील्ड्स का उदाहरण भी माना जा सकता है)। मल्टीपोल विस्तार के संदर्भ में सामान्य प्रवाह पैटर्न को भी विघटित किया जा सकता है, उसी तरह जैसे विद्युत क्षेत्र और चुंबकीय क्षेत्र क्षेत्रों के लिए जहां मोनोपोल अनिवार्य रूप से विस्तार का पहला गैर-तुच्छ (जैसे स्थिर) शब्द है।

यह प्रवाह पैटर्न इर्रोटेशनल और असम्पीडित दोनों है।

यह एक बेलनाकार समरूपता की विशेषता है:

$\mathbf {v} =v_{r}(r)\mathbf {e} _{r}$

जहां कुल आउटगोइंग फ्लक्स स्थिर है

$\int _{S}\mathbf {v} \cdot d\mathbf {S} =\int _{0}^{2\pi }(v_{r}(r)\,\mathbf {e} _{r})\cdot (\mathbf {e} _{r}\,r\,d\theta )=\!2\pi \,r\,v_{r}(r)=Q$

इसलिए,

$v_{r}={\frac {Q}{2\pi r}}$

यह एक स्ट्रीम फ़ंक्शन से लिया गया है

$\psi (r,\theta )=-{\frac {Q}{2\pi }}\theta$

या एक संभावित कार्य से

$\phi (r,\theta )=-{\frac {Q}{2\pi }}\ln r$

द्वि-आयामी रेखा सिंक

एक निश्चित दर पर एक निश्चित मात्रा में द्रव Q प्रति यूनिट लंबाई को अवशोषित करने वाली एक ऊर्ध्वाधर रेखा का मामला एक लाइन सिंक है। सब कुछ वैसा ही है जैसा ऋणात्मक चिन्ह से एक भाग के स्रोत की रेखा के मामले में होता है।

$v_{r}=-{\frac {Q}{2\pi r}}$

यह एक स्ट्रीम फ़ंक्शन से लिया गया है

$\psi (r,\theta )={\frac {Q}{2\pi }}\theta$

या एक संभावित कार्य से

$\phi (r,\theta )={\frac {Q}{2\pi }}\ln r$

यह देखते हुए कि दो परिणाम एक ऋण चिह्न से एक ही भाग हैं, हम पारदर्शी रूप से लाइन स्रोतों और लाइन सिंक दोनों को एक ही धारा और संभावित कार्यों के साथ इलाज कर सकते हैं जिससे क्यू को सकारात्मक और नकारात्मक दोनों मूल्यों को ग्रहण करने और क्यू की परिभाषा में ऋण चिह्न को अवशोषित करने की अनुमति मिलती है। .

द्वि-आयामी द्विध्रुव या द्विध्रुवीय रेखा स्रोत

एक आदर्श द्विध्रुव, या द्विध्रुवीय, रेखा के लिए संभावित प्रवाह स्ट्रीमलाइन, स्ट्रीकलाइन और पाथलाइन

यदि हम d दूरी पर एक लाइन स्रोत और एक लाइन सिंक पर विचार करते हैं, तो हम उपरोक्त परिणामों का पुन: उपयोग कर सकते हैं और स्ट्रीम फ़ंक्शन होगा

$\psi (\mathbf {r} )=\psi _{Q}(\mathbf {r} -\mathbf {d} /2)-\psi _{Q}(\mathbf {r} +\mathbf {d} /2)\ \simeq \mathbf {d} \cdot \nabla \psi _{Q}(\mathbf {r} )$

अंतिम सन्निकटन d में पहले क्रम का है।

दिया गया

$\mathbf {d} =d[\cos(\theta _{0})\mathbf {e} _{x}+\sin(\theta _{0})\mathbf {e} _{y}]=d[\cos(\theta -\theta _{0})\mathbf {e} _{r}+\sin(\theta -\theta _{0})\mathbf {e} _{\theta }]$

यह बनी हुई है

$\psi (r,\theta )=-{\frac {Qd}{2\pi }}{\frac {\sin(\theta -\theta _{0})}{r}}$

वेग तो है

$v_{r}(r,\theta )={\frac {Qd}{2\pi }}{\frac {\cos(\theta -\theta _{0})}{r^{2}}}$

$v_{\theta }(r,\theta )={\frac {Qd}{2\pi }}{\frac {\sin(\theta -\theta _{0})}{r^{2}}}$

और इसके बजाय संभावित

$\phi (r,\theta )={\frac {Qd}{2\pi }}{\frac {\cos(\theta -\theta _{0})}{r}}$

द्वि-आयामी भंवर रेखा

एक आदर्श भंवर रेखा के लिए संभावित प्रवाह स्ट्रीमलाइन, स्ट्रीकलाइन और पाथलाइन

यह एक भंवर फिलामेंट का मामला है जो निरंतर गति से घूमता है, एक बेलनाकार समरूपता होती है और ऑर्थोगोनल प्लेन में समस्या को हल किया जा सकता है।

रेखा स्रोतों के ऊपर के मामले में दोहरी, भंवर रेखाएं इरोटेशनल प्रवाह के लिए मोनोपोल की भूमिका निभाती हैं।

इसके अलावा इस मामले में प्रवाह भी इरोटेशनल फ्लो और इनकंप्रेसिबल फ्लो दोनों है और इसलिए संभावित प्रवाह का मामला है।

यह एक बेलनाकार समरूपता की विशेषता है:

$\mathbf {v} =v_{\theta }(r)\,\mathbf {e} _{\theta }$

जहां केंद्रीय भंवर के चारों ओर प्रत्येक बंद रेखा के लिए कुल संचलन स्थिर है

$\oint \mathbf {v} \cdot d\mathbf {s} =\int _{0}^{2\pi }(v_{\theta }(r)\,\mathbf {e} _{\theta })\cdot (\mathbf {e} _{\theta }\,r\,d\theta )=\!2\pi \,r\,v_{\theta }(r)=\Gamma$

और भंवर सहित किसी भी रेखा के लिए शून्य है।

इसलिए,

$v_{\theta }={\frac {\Gamma }{2\pi r}}$

यह एक स्ट्रीम फ़ंक्शन से लिया गया है

$\psi (r,\theta )={\frac {\Gamma }{2\pi }}\ln r$

या एक संभावित कार्य से

$\phi (r,\theta )=-{\frac {\Gamma }{2\pi }}\theta$

जो एक लाइन स्रोत के पिछले मामले से दोहरा है

सामान्य द्वि-आयामी संभावित प्रवाह

एक असंपीड़ित द्वि-आयामी प्रवाह को देखते हुए जो हमारे पास अघूर्णी भी है:

$\nabla ^{2}\psi =0$

जो बेलनाकार निर्देशांक में है

${\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}\psi }{\partial \theta ^{2}}}=0$

हम अलग-अलग चर वाले समाधान की तलाश करते हैं:

$\psi (r,\theta )=R(r)\Theta (\theta )$

जो देता है

${\frac {r}{R(r)}}{\frac {d}{dr}}\left(r{\frac {dR(r)}{dr}}\right)=-{\frac {1}{\Theta (\theta )}}{\frac {d^{2}\Theta (\theta )}{d\theta ^{2}}}$

दिया गया बायाँ भाग केवल r पर निर्भर करता है और दायाँ भाग केवल पर निर्भर करता है $\theta$, दो भागों r और से स्वतंत्र एक स्थिरांक के बराबर होना चाहिए $\theta$. स्थिरांक धनात्मक होगा. इसलिए,

$r{\frac {d}{dr}}\left(r{\frac {d}{dr}}R(r)\right)=m^{2}R(r)$

${\frac {d^{2}\Theta (\theta )}{d\theta ^{2}}}=-m^{2}\Theta (\theta )$

दूसरे समीकरण का हल एक रैखिक संयोजन है $e^{im\theta }$ और $e^{-im\theta }$ एकल-मूल्यवान वेग (और एकल-मूल्यवान धारा फ़ंक्शन) के लिए m एक धनात्मक पूर्णांक होगा।

इसलिए सबसे सामान्य समाधान द्वारा दिया गया है

$\psi =\alpha _{0}+\beta _{0}\ln r+\sum _{m>0}{\left(\alpha _{m}r^{m}+\beta _{m}r^{-m}\right)\sin {[m(\theta -\theta _{m})]}}$

इसके बजाय संभावित द्वारा दिया गया है

$\phi =\alpha _{0}-\beta _{0}\theta +\sum _{m\mathop {>} 0}{(\alpha _{m}r^{m}-\beta _{m}r^{-m})\cos {[m(\theta -\theta _{m})]}}$

संदर्भ

• Fitzpatrick, Richard (2017), Theoretical fluid dynamics, IOP science, ISBN 978-0-7503-1554-8
• Faber, T.E. (1995), Fluid Dynamics for Physicists, Cambridge university press, ISBN 9780511806735

Specific

अग्रिम पठन

• Batchelor, G.K. (1973), An introduction to fluid dynamics, Cambridge University Press, ISBN 978-0-521-09817-5
• Chanson, H. (2009), Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows, CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 478 pages, ISBN 978-0-415-49271-3
• Lamb, H. (1994) [1932], Hydrodynamics (6th ed.), Cambridge University Press, ISBN 978-0-521-45868-9
• Milne-Thomson, L.M. (1996) [1968], Theoretical hydrodynamics (5th ed.), Dover, ISBN 978-0-486-68970-8

बाहरी संबंध

• Richard Fitzpatrick University of Texas, Austin (2017). "Fluid Mechanics". University of Texas, Austin. Retrieved 2018-02-07.

• (c) Aerospace, Mechanical & Mechatronic Engg. 2005 University of Sydney (2005). "Elements of Potential Flow". University of Sydney. Retrieved 2019-04-19.