युग्मन स्थिरांक

For बीईसी में बोसोन के बीच पारस्परिक क्रिया, see सकल-पितावस्की समीकरण § समीकरण का रूप. For मरे-वॉन न्यूमैन युग्मन स्थिरांक, see वॉन न्यूमैन बीजगणित. For एनएमआर स्पेक्ट्रोस्कोपी में युग्मन स्थिरांक, see परमाणु चुंबकीय अनुनाद स्पेक्ट्रोस्कोपी. For और, see प्रोटॉन एनएमआर. For ग्रंथमिति में युग्मन शक्ति, see ग्रंथ सूची युग्मन.

भौतिकी में, एक युग्मन स्थिरांक या गेज युग्मन पैरामीटर (या, अधिक सरलता से, एक युग्मन), एक संख्या है जो मौलिक अन्योन्यक्रिया में लगाए गए बल के सामर्थ्य को निर्धारित करती है। मूल रूप से, युग्मन स्थिरांक दो स्थिर पिंडों के बीच कार्य करने वाले बल को पिंडों के आवेश (भौतिकी) से संबंधित करता है (अर्थात स्थिरवैद्युतिकी के लिए विद्युत आवेश और न्यूटन के सार्वभौमिक गुरुत्वाकर्षण के नियम के लिए द्रव्यमान) से संबंधित होता है, जो पिंडों के बीच की दूरी वर्ग, $r^{2}$,से विभाजित होता है; इस प्रकार: न्यूटोनियन गुरुत्वाकर्षण के लिए $F=Gm_{1}m_{2}/r^{2}$ में $G$ और स्थिरवैद्युतिकी के लिए $F=k_{\text{e}}q_{1}q_{2}/r^{2}$में $k_{\text{e}}$। यह विवरण आधुनिक भौतिकी में स्थैतिक पिंडों और द्रव्यमान रहित बल वाहकों के साथ अध्यारोपण सिद्धांत के लिए मान्य है।

एक आधुनिक और अधिक सामान्य परिभाषा प्रणाली के लग्रांजी(क्षेत्र सिद्धांत) ${\mathcal {L}}$ ( या समकक्ष रूप से हैमिल्टनियन यांत्रिकी ${\mathcal {H}}$) का उपयोग करती है। सामान्यतः, अन्योन्यक्रिया का वर्णन करने वाली प्रणाली के ${\mathcal {L}}$ (या ${\mathcal {H}}$) को एक गतिज भाग $T$ और एक अन्योन्यक्रिया भाग $V$: ${\mathcal {L}}=T-V$ (या ${\mathcal {H}}=T+V$) में अलग किया जा सकता है। क्षेत्र सिद्धांत में, $V$ में सदैव 3 क्षेत्र पद या अधिक होते हैं, उदाहरण के लिए यह व्यक्त करते हुए कि एक प्रारंभिक इलेक्ट्रॉन (क्षेत्र 1) ने एक फोटॉन (क्षेत्र 2) के साथ अन्योन्यक्रिया की, जो इलेक्ट्रॉन की अंतिम स्थिति (क्षेत्र 3) का उत्पादन करता है। इसके विपरीत, गतिज भाग $T$ में सदैव मात्र दो क्षेत्र होते हैं, जो प्रारंभिक कण (क्षेत्र 1) के बाद की स्थिति (क्षेत्र 2) में मुक्त प्रसार को व्यक्त करते हैं। युग्मन स्थिरांक $V$ भाग के संबंध में $T$ भाग के परिमाण को निर्धारित करता है (या अंतःक्रियात्मक भाग के दो क्षेत्रों के बीच यदि कई क्षेत्र अलग-अलग स्थित हैं)। उदाहरण के लिए, एक कण का विद्युत आवेश एक युग्मन स्थिरांक है जो दो आवेश-वहन करने वाले क्षेत्रों और एक फोटॉन क्षेत्र (इसलिए दो तीरों और एक तरंगिल रेखा के साथ सामान्य फेनमैन आरेख) के साथ अन्योन्यक्रिया की विशेषता है। चूंकि फोटॉन विद्युत चुंबकत्व बल की मध्यस्थता करते हैं, इसलिए यह युग्मन निर्धारित करता है कि इलेक्ट्रॉनों को इस प्रकार की सामर्थ्य कितनी प्रबलता से अनुभव होती है, और इसका मान प्रयोग द्वारा निर्धारित किया जाता है। लग्रांजी (क्षेत्र सिद्धांत) को देखकर, कोई देखता है कि वस्तुतः, युग्मन गतिज पद $T={\bar {\psi }}(i\hbar c\gamma ^{\sigma }\partial _{\sigma }-mc^{2})\psi -{1 \over 4\mu _{0}}F_{\mu \nu }F^{\mu \nu }$ और अन्योन्यक्रिया पद $V=-e{\bar {\psi }}(\hbar c\gamma ^{\sigma }A_{\sigma })\psi$ के बीच आनुपातिकता निर्धारित करता है ।

गतिकी में एक युग्मन महत्वपूर्ण भूमिका निभाता है। उदाहरण के लिए, प्रायः विभिन्न युग्मन स्थिरांक के महत्व के आधार पर सन्निकटन के पदानुक्रम स्थापित करता है। चुंबकीय लोहे की एक बड़ी गांठ की गति में, युग्मन स्थिरांक के सापेक्ष परिमाण के कारण चुंबकीय बल गुरुत्वाकर्षण बल से अधिक महत्वपूर्ण हो सकते हैं। यद्यपि, चिरसम्मत यांत्रिकी में, सामान्यतः इन निर्णयों को सीधे बलों की तुलना करके किया जाता है। युग्मन स्थिरांक द्वारा निभाई गई केंद्रीय भूमिका का एक अन्य महत्वपूर्ण उदाहरण यह है कि वे प्रक्षोभ सिद्धांत पर आधारित प्रथम-सिद्धांत गणना के लिए विस्तार पैरामीटर हैं, जो भौतिकी की कई शाखाओं में गणना की मुख्य विधि है।

सूक्ष्म संरचना स्थिरांक

क्वांटम क्षेत्र सिद्धांत में युग्मन स्वाभाविक रूप से उत्पन्न होते हैं। आयामहीन युग्मन द्वारा सापेक्षतावादी क्वांटम सिद्धांतों में एक विशेष भूमिका निभाई जाती है; अर्थात्, शुद्ध संख्याएँ हैं। एक आयाम रहित स्थिरांक का एक उदाहरण सूक्ष्म संरचना स्थिरांक है,

$\alpha ={\frac {e^{2}}{4\pi \varepsilon _{0}\hbar c}},$

जहां e एक इलेक्ट्रॉन का आवेश है, $\varepsilon _{0}$ मुक्त स्थान की पारगम्यता है, ℏ समानीत प्लैंक स्थिरांक है और c प्रकाश की गति है। यह स्थिरांक विद्युत चुम्बकीय क्षेत्र में एक इलेक्ट्रॉन के आवेश की युग्मन सामर्थ्य के वर्ग के समानुपाती होता है।

गेज युग्मन

गैर-एबेलियन गेज सिद्धांत में, गेज युग्मन पैरामीटर, $g$, लग्रांजी (क्षेत्र सिद्धांत) में

${\frac {1}{4g^{2}}}{\rm {Tr}}\,G_{\mu \nu }G^{\mu \nu },$

(जहाँ G गेज क्षेत्र (भौतिकी) प्रदिश है) के रूप में कुछ परिपाटी में प्रकट होता है। एक अन्य व्यापक रूप से उपयोग किए जाने वाले परिपाटी में, G पुनर्निर्धारित किया जाता है ताकि गतिज पद का गुणांक 1/4 हो और$g$सहपरिवर्ती व्युत्पन्न में प्रकट हो। इसे

${\frac {e}{\sqrt {\varepsilon _{0}\hbar c}}}={\sqrt {4\pi \alpha }}\approx 0.30282212\ ~~$

के रूप में परिभाषित मूल आवेश के एक आयाम रहित संस्करण के समान समझा जाना चाहिए

शिथिल और प्रबल युग्मन

युग्मन g के साथ क्वांटम क्षेत्र सिद्धांत में, यदि g 1 से बहुत कम है, तो सिद्धांत को शिथिल युग्मित कहा जाता है। इस स्थिति में, यह g के सामर्थ्य में विस्तार से वर्णित है, जिसे प्रक्षोभ सिद्धांत (क्वांटम यांत्रिकी) कहा जाता है। यदि युग्मन स्थिरांक एक या अधिक क्रम का है, तो सिद्धांत को प्रबलता से युग्मित कहा जाता है। उत्तरार्द्ध का एक उदाहरण प्रबल अंतःक्रियाओं का हैड्रोनिक सिद्धांत है (यही कारण है कि इसे पहले स्थान पर प्रबल कहा जाता है)। ऐसी स्थिति में, सिद्धांत की जांच के लिए गैर-उत्तेजित करने वाली विधियों का उपयोग किया जाना चाहिए।

क्वांटम क्षेत्र सिद्धांत में, युग्मन का आयाम सिद्धांत के पुनर्सामान्यीकरण में महत्वपूर्ण भूमिका निभाता है, और इसलिए प्रक्षोभ सिद्धांत की प्रयोज्यता पर। यदि युग्मन प्राकृतिक इकाइयों में आयामहीन है (अर्थात $c=1$, $\hbar =1$), क्यूईडी, क्यूसीडी, और शिथिल अन्योन्यक्रिया के जैसे, सिद्धांत पुनर्सामान्यीकरण योग्य है और विस्तार श्रृंखला के सभी प्रतिबन्ध परिमित हैं (पुनर्नवीनीकरण के बाद)। यदि युग्मन विमीय है, उदा. गुरुत्वाकर्षण ($[G_{N}]={\text{energy}}^{-2}$) में, फर्मी की अन्योन्यक्रिया ($[G_{F}]={\text{energy}}^{-2}$) या प्रबल बल ($[F]={\text{energy}}$) का चिराल प्रक्षोभ सिद्धांत, तो सिद्धांत सामान्यतः पुन: सामान्य नहीं होता है। युग्मन में प्रक्षोभ का विस्तार अभी भी संभव हो सकता है, यद्यपि सीमाओं के भीतर, क्योंकि श्रृंखला के अधिकांश उच्च क्रम के पद अनंत होंगे।

संचालन युग्मन

अंजीर। 1 आभासी कण युग्मन renormalize

उपयोग की गई जांच के तरंग दैर्ध्य या संवेग, k को बदलकर कम समय या दूरी पर एक क्वांटम क्षेत्र सिद्धांत की जांच की जा सकती है। एक उच्च आवृत्ति (अर्थात, कम समय) जांच के साथ, आभासी कण प्रत्येक प्रक्रिया में भाग लेते हुए देखते हैं। ऊर्जा के संरक्षण के इस स्पष्ट उल्लंघन को अनिश्चितता संबंध

$\Delta E\Delta t\geq {\frac {\hbar }{2}}$

की जांच करके अनुमान के रूप से समझा जा सकता है जो वस्तुतः कम समय में ऐसे उल्लंघनों की अनुमति देता है। पूर्वगामी टिप्पणी मात्र क्वांटम क्षेत्र सिद्धांत के कुछ योगों पर लागू होती है, विशेष रूप से, अंतःक्रिया चित्र में विहित परिमाणीकरण।

अन्य योगों में, समान घटना का वर्णन आभासी कणों द्वारा द्रव्यमान कोश से बाहर जाने के द्वारा वर्णित किया गया है। ऐसी प्रक्रियाएं युग्मन का पुनर्सामान्यीकरण करती हैं और इसे ऊर्जा पैमाने, μ पर निर्भर करती हैं, जिस पर युग्मन की जांच की जाती है। ऊर्जा-पैमाने पर युग्मन g(μ) की निर्भरता को युग्मन के संचालन के रूप में जाना जाता है। युग्मन के संचालन का सिद्धांत पुनर्सामान्यीकरण समूह द्वारा दिया गया है, यद्यपि यह ध्यान में रखा जाना चाहिए कि पुनर्सामान्यीकरण समूह एक अधिक सामान्य अवधारणा है जो भौतिक प्रणाली में किसी भी प्रकार के पैमाने भिन्नता का वर्णन करता है (विवरण के लिए पूरा लेख देखें)।

एक युग्मन के संचालन की घटना

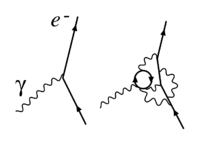
पुनर्सामान्यीकरण समूह एक युग्मन के संचालन को प्राप्त करने के लिए एक औपचारिक तरीका प्रदान करता है, फिर भी संचालन वाली घटनाओं को सहज रूप से समझा जा सकता है। जैसा कि परिचय में समझाया गया है, युग्मन स्थिरांक एक बल का परिमाण निर्धारित करता है जो दूरी के साथ $1/r^{2}$ के रूप में व्यवहार करता है। $1/r^{2}$-निर्भरता को पहली बार माइकल फैराडे द्वारा बल प्रवाह की कमी के रूप में समझाया गया था: निकाय A से $r$ द्वारा दूर एक बिंदु B दूपर एक बल उत्पन्न होता है, यह क्षेत्र के प्रवाह के समानुपाती होता है जो रेखा AB के लिए जाने वाले क्षेत्र प्रवाह के समानुपाती होता है। चूंकि प्रवाह समष्टि के माध्यम से समान रूप से फैलता है, यह सतह S को बनाए रखने वाले ठोस कोण के अनुसार घटता है। क्वांटम क्षेत्र सिद्धांत के आधुनिक दृष्टिकोण में, $1/r^{2}$ बल वाहकों के प्रचारक की स्थिति और संवेग स्थान में अभिव्यक्ति से आता है। अपेक्षाकृत शिथिल रूप से परस्पर क्रिया करने वाले पिंडों के लिए, जैसा कि सामान्यतः विद्युत चुंबकत्व या गुरुत्वाकर्षण या कम दूरी पर परमाणु अन्योन्यक्रिया में होता है, बोर्न सन्निकटन पिंडों के बीच परस्पर क्रिया का एक ठीक पहला सन्निकटन है, और चिरसम्मत रूप से अंतःक्रिया एक $1/r^{2}$-नियम का पालन करेगी (ध्यान दें कि यदि बल वाहक भारी है, तो अतिरिक्त $r$ निर्भरता है)। जब अन्योन्य क्रियाएं अधिक तीव्र होती हैं (उदाहरण के लिए आवेश या द्रव्यमान बड़ा होता है, या $r$ छोटा होता है) या कम समय अवधि (छोटे $r$) पर होता है, तो अधिक बल वाहक शामिल हैं या जोड़ी उत्पादन बनाया जाता है, चित्र 1 देखें, जिसके परिणामस्वरूप ब्रेक-डाउन हो जाता है $1/r^{2}$ व्यवहार। चिरसम्मत समकक्ष यह है कि फील्ड फ्लक्स अब समष्टि में स्वतंत्र रूप से प्रचार नहीं करता है, लेकिन उदा। अतिरिक्त आभासी कणों के आवेशों, या इन आभासी कणों के बीच अन्योन्यक्रिया से विद्युत-क्षेत्र स्क्रीनिंग से गुजरता है। पहले क्रम को अलग करना सुविधाजनक है $1/r^{2}$ इस अतिरिक्त से नियम $r$-निर्भरता। इसके बाद बाद में युग्मन में शामिल होने के कारण इसका हिसाब लगाया जाता है, जो तब बन जाता है $1/r$-निर्भर, (या समकक्ष μ-निर्भर)। चूँकि एकल बल वाहक सन्निकटन से परे शामिल अतिरिक्त कण सदैव आभासी कण होते हैं, अर्थात क्षणिक क्वांटम क्षेत्र में उतार-चढ़ाव, कोई यह समझता है कि युग्मन का चलना एक वास्तविक क्वांटम और सापेक्षतावादी घटना क्यों है, अर्थात् उच्च-क्रम फेनमैन आरेखों का प्रभाव। बल के सामर्थ्य।

चूंकि चल रहे युग्मन सूक्ष्म क्वांटम प्रभावों के लिए प्रभावी रूप से खाते हैं, इसलिए इसे लैग्रैंगियन या हैमिल्टनियन में स्थित नंगे युग्मन (स्थिर) के विपरीत प्रायः एक प्रभावी युग्मन कहा जाता है।

बीटा कार्य

Main article: Beta function (physics)

क्वांटम क्षेत्र सिद्धांत में, एक बीटा फ़ंक्शन, β(g), एक युग्मन पैरामीटर, g के संचालन को कूटबद्ध करता है। यह संबंध द्वारा परिभाषित किया गया है

$\beta (g)=\mu {\frac {\partial g}{\partial \mu }}={\frac {\partial g}{\partial \ln \mu }},$

जहाँ μ दी गई भौतिक प्रक्रिया का ऊर्जा पैमाना है। यदि क्वांटम फील्ड थ्योरी के बीटा फ़ंक्शंस गायब हो जाते हैं, तो सिद्धांत अनुरूप क्षेत्र सिद्धांत | स्केल-इनवेरिएंट है।

क्वांटम क्षेत्र सिद्धांत के युग्मन पैरामीटर प्रवाहित हो सकते हैं, भले ही संबंधित चिरसम्मत क्षेत्र (भौतिकी) सिद्धांत स्केल इनवेरियन | स्केल-इनवेरिएंट हो। इस स्थिति में, गैर-शून्य बीटा फ़ंक्शन हमें बताता है कि क्लासिकल स्केल-इनवेरिएंस अनुरूप विसंगति है।

क्यूईडी और लैंडौ पोल

यदि कोई बीटा फ़ंक्शन धनात्मक है, तो बढ़ती ऊर्जा के साथ संबंधित युग्मन बढ़ता है। एक उदाहरण क्वांटम इलेक्ट्रोडायनामिक्स (क्यूईडी) है, जहां कोई प्रक्षोभ सिद्धांत (क्वांटम यांत्रिकी) का उपयोग करके पाता है कि बीटा फ़ंक्शन (भौतिकी) # उदाहरण सकारात्मक है। विशेष रूप से, कम ऊर्जा पर, α ≈ 1/137, जबकि Z बोसॉन के पैमाने पर, लगभग 90 GeV, एक माप α ≈ 1/127।

इसके अलावा, पर्टुरेटिव बीटा फ़ंक्शन हमें बताता है कि युग्मन में वृद्धि जारी है, और QED उच्च ऊर्जा पर प्रबलता से युग्मित हो जाता है। वस्तुतः कुछ परिमित ऊर्जा पर युग्मन स्पष्ट रूप से अनंत हो जाता है। इस घटना को सबसे पहले लेव लैंडौ ने नोट किया था, और इसे लैंडौ पोल कहा जाता है। यद्यपि, कोई उम्मीद नहीं कर सकता है कि परेशान करने वाला बीटा फ़ंक्शन प्रबल युग्मन पर सटीक परिणाम देता है, और इसलिए यह संभावना है कि लैंडौ पोल प्रक्षोभ सिद्धांत को ऐसी स्थिति में लागू करने का एक आर्टिफैक्ट है जहां यह अब मान्य नहीं है। का सही स्केलिंग व्यवहार $\alpha$ बड़ी ऊर्जाओं पर ज्ञात नहीं है।

क्यूसीडी और स्पर्शोन्मुख स्वतंत्रता

गैर-एबेलियन गेज सिद्धांतों में, बीटा फ़ंक्शन नकारात्मक हो सकता है, जैसा कि पहले फ्रैंक विल्जेक, डेविड पोलित्जर और डेविड ग्रॉस ने पाया था। इसका एक उदाहरण बीटा फ़ंक्शन (भौतिकी) #क्वांटम क्रोमोडायनामिक्स (QCD) के उदाहरण हैं, और परिणामस्वरूप उच्च ऊर्जा पर QCD युग्मन घट जाता है।

इसके अलावा, युग्मन लघुगणकीय रूप से घटता है, एक घटना जिसे स्पर्शोन्मुख स्वतंत्रता के रूप में जाना जाता है (जिसकी खोज को 2004 में भौतिकी में नोबेल पुरस्कार से सम्मानित किया गया था)। युग्मन लगभग घट जाता है

$\alpha _{\text{s}}(k^{2})\ {\stackrel {\mathrm {def} }{=}}\ {\frac {g_{\text{s}}^{2}(k^{2})}{4\pi }}\approx {\frac {1}{\beta _{0}\ln \left({k^{2}}/{\Lambda ^{2}}\right)}},$

जहां बी₀ Wilczek, Gross और Politzer द्वारा पहली बार परिकलित एक स्थिरांक है।

इसके विपरीत, घटती ऊर्जा के साथ युग्मन बढ़ता है। इसका मतलब यह है कि युग्मन कम ऊर्जा पर बड़ा हो जाता है, और कोई भी प्रक्षोभ सिद्धांत (क्वांटम यांत्रिकी) पर भरोसा नहीं कर सकता है। इसलिए, युग्मन स्थिरांक का वास्तविक मान मात्र दिए गए ऊर्जा पैमाने पर परिभाषित किया गया है। QCD में, Z बोसोन मास स्केल को सामान्यतः चुना जाता है, जो α के प्रबल युग्मन स्थिरांक का मान प्रदान करता है_s(एम_Z² ) = 0.1179 ± 0.0010। जाली क्यूसीडी गणनाओं, ताऊ-लिप्टन क्षय के अध्ययन के साथ-साथ जेड बोसोन के अनुप्रस्थ गति स्पेक्ट्रम की पुनर्व्याख्या से सबसे सटीक माप उत्पन्न होते हैं।

क्यूसीडी स्केल

क्वांटम क्रोमोडायनामिक्स (QCD) में, मात्रा Λ को QCD स्केल कहा जाता है। मान है $\Lambda _{\rm {MS}}=332\pm 17{\text{ MeV}}$तीन सक्रिय क्वार्क स्वादों के लिए, अर्थात जब प्रक्रिया में शामिल ऊर्जा-संवेग मात्र ऊपर, नीचे और अजीब क्वार्क उत्पन्न करने की अनुमति देता है, लेकिन भारी क्वार्क नहीं। यह 1.275 GeV से कम ऊर्जा के अनुरूप है। उच्च ऊर्जा पर, Λ छोटा होता है, उदा. $\Lambda _{\rm {MS}}=210\pm 14$ एमईवी लगभग 5 GeV के निचले क्वार्क द्रव्यमान के ऊपर। न्यूनतम घटाव योजना (एमएस) योजना पैमाने का अर्थ Λ_MS आयामी प्रसारण पर लेख में दिया गया है। प्रोटॉन-टू-इलेक्ट्रॉन जन अनुपात मुख्य रूप से क्यूसीडी पैमाने द्वारा निर्धारित किया जाता है।

स्ट्रिंग सिद्धांत

स्ट्रिंग थ्योरी में एक उल्लेखनीय भिन्न स्थिति स्थित है क्योंकि इसमें एक dilaton शामिल है। स्ट्रिंग स्पेक्ट्रम के एक विश्लेषण से पता चलता है कि यह क्षेत्र स्थित होना चाहिए, या तो बोसोनिक स्ट्रिंग या नेफ्यू-श्वार्ज़-रामोंड थोंग|एनएस-एनएस सुपरस्ट्रिंग का क्षेत्र। वर्टेक्स ऑपरेटरों का उपयोग करते हुए, यह देखा जा सकता है कि रोमांचक यह क्षेत्र क्रिया में एक पद जोड़ने के बराबर है जहां एक अदिश क्षेत्र रिक्की अदिश से जुड़ता है। इसलिए यह क्षेत्र युग्मन स्थिरांक का एक संपूर्ण कार्य है। ये युग्मन स्थिरांक पूर्व-निर्धारित, समायोज्य, या सार्वभौमिक पैरामीटर नहीं हैं; वे समष्टि और समय पर एक प्रकार से निर्भर करते हैं जो गतिशील रूप से निर्धारित होता है। स्रोत जो स्ट्रिंग युग्मन का वर्णन करते हैं जैसे कि यह निर्धारित किया गया था, सामान्यतः वैक्यूम अपेक्षा मान का जिक्र कर रहे हैं। यह बोसोनिक सिद्धांत में कोई मान रखने के लिए स्वतंत्र है जहां कोई सुपरपोटेंशियल नहीं है।

यह भी देखें

• विहित परिमाणीकरण, पुनर्सामान्यीकरण और आयामी नियमितीकरण
• ललित-संरचना स्थिरांक
• क्वांटम फील्ड थ्योरी, विशेष रूप से क्वांटम इलेक्ट्रोडायनामिक्स और क्वांटम क्रोमोडायनामिक्स
• ग्लूऑन फील्ड, ग्लूऑन फील्ड स्ट्रेंथ टेंसर

बाहरी संबंध

• The Nobel Prize in Physics 2004 – Information for the Public
• Department of Physics and Astronomy of the Georgia State University - Coupling Constants for the Fundamental Forces
• An introduction to quantum field theory, by M.E.Peskin and H.D.Schroeder, ISBN 0-201-50397-2