चतुर्थांश (साधन)

From Vigyanwiki
Revision as of 08:58, 24 April 2023 by alpha>Saurabh
बीजिंग प्राचीन वेधशाला में बड़ा फ्रेम चतुर्थांश। इसका निर्माण 1673 में किया गया था।

चतुर्थांश मापक यंत्र है जिसका उपयोग समकोण 90° तक के कोणों को मापने के लिए किया जाता है। देशांतर, अक्षांश और नागरिक समय जैसे विभिन्न रीडिंग की गणना के लिए इस उपकरण के विभिन्न संस्करणों का उपयोग किया जा सकता है। इसका सबसे पहला सूची किया गया उपयोग प्राचीन भारत में वैदिक काल में अत्री द्वारा सूर्य ग्रहण देखने के लिए किया गया था।[1][2] यह तब टॉलेमी द्वारा उत्तम प्रकार के यंत्र के रूप में प्रस्तावित किया गया था।[3] साधन के कई अलग-अलग रूप बाद में मध्यकालीन मुस्लिम खगोलविदों द्वारा निर्मित किए गए थे। 18 वीं शताब्दी की खगोलीय वेधशालाओं की यूरोपीय सूची में भित्ति चतुर्थांश खगोलीय उपकरणों की महत्वपूर्ण सूची थी, जो गोलाकार खगोल विज्ञान के लिए उपयोग की स्थापना करती थी।

व्युत्पत्ति

चतुर्थांश शब्द, जिसका अर्थ चौथाई है, इस तथ्य को संदर्भित करता है कि उपकरण के प्रारंभिक संस्करण एस्ट्रोलैब से प्राप्त किए गए थे। चतुर्भुज ने एस्ट्रोलैब के कार्यवाहक को एस्ट्रोलैब के चेहरे के चौथाई आकार के क्षेत्र में संघनित किया; यह अनिवार्य रूप से एस्ट्रोलैब का चौथाई था।

इतिहास

टॉलेमी चतुर्थांश का उपयोग करते हुए
एक तुर्की चित्रण में चतुर्भुज

प्राचीन भारत में वैदिक काल के समय , बड़े सूर्य ग्रहण की सीमा को मापने के लिए 'तुरीयम' नामक चतुर्भुज का उपयोग किया जाता था। ऋग्वेद के पांचवें मंडल में अत्रि द्वारा सूर्य ग्रहण देखने के लिए तुरीयम के उपयोग का वर्णन किया गया है,[1][2] सी के बीच सबसे अधिक संभावना 1500 और 1000 ईसा पूर्व है।[4]

150 ईस्वी के आसपास टॉलेमी के अल्मागेस्ट से चतुर्भुज के प्रारंभिक खाते भी आते हैं। उन्होंने प्लिंथ का वर्णन किया जो 90 डिग्री के स्नातक किए गए चाप पर खूंटी की छाया को प्रक्षेपित करके दोपहर के सूरज की ऊंचाई को माप सकता है।[5] यह चतुर्भुज उपकरण के बाद के संस्करणों के विपरीत था; यह बड़ा था और इसमें कई चलने वाले भाग सम्मिलित थे। टॉलेमी का संस्करण एस्ट्रोलैब का व्युत्पन्न था और इस अल्पविकसित उपकरण का उद्देश्य सूर्य के मध्याह्न कोण को मापना था।

मध्य युग में मुस्लिम खगोलविदों ने इन विचारों में सुधार किया और पूरे मध्य पूर्व में मारघेह वेधशाला, रे, ईरान और समरक़ंद जैसी वेधशालाओं में चतुष्कोणों का निर्माण किया था। पहले ये चतुर्भुज सामान्यतः बहुत बड़े और स्थिर थे, और किसी भी खगोलीय पिंड के लिए ऊंचाई और दिगंश दोनों देने के लिए किसी भी असर में घुमाया जा सकता था।[6] जैसा कि मुस्लिम खगोलविदों ने खगोलीय सिद्धांत और अवलोकन संबंधी स्पष्टता में प्रगति की है, उन्हें मध्य युग और उसके बाद चार अलग-अलग प्रकार के चतुष्कोण विकसित करने का श्रेय दिया जाता है। इनमें से पहला, ज्या चतुर्भुज, का आविष्कार मुहम्मद इब्न मूसा अल-ख्वारिज्मी ने 9वीं शताब्दी में बगदाद में ज्ञान का घर में किया था।[7]: 128  अन्य प्रकार सार्वभौमिक चतुर्भुज, भयानक चतुर्भुज और एस्ट्रोलैब चतुर्भुज थे।

मध्य युग के समय इन उपकरणों का ज्ञान यूरोप में फैल गया। 13वीं शताब्दी में यहूदी खगोलशास्त्री याकूब बिन मुशीर बिन तैयबौन चतुर्थांश को और विकसित करने में महत्वपूर्ण थे।[8] वह कुशल खगोलशास्त्री थे और उन्होंने इस विषय पर कई खंड लिखे, जिसमें प्रभावशाली पुस्तक भी सम्मिलित है, जिसमें बताया गया है कि वृत्तखंड के उत्तम संस्करण का निर्माण और उपयोग कैसे किया जाए। उन्होंने जिस चतुर्भुज का आविष्कार किया, उसे नए चतुर्भुज या नए चतुर्भुज के रूप में जाना जाने लगा है।[9] यह उपकरण क्रांतिकारी था क्योंकि यह निर्मित होने वाला पहला चतुर्भुज था जिसमें कई चलने वाले भाग सम्मिलित नहीं थे और इस प्रकार यह बहुत छोटा और अधिक वहनीय हो सकता था।

टिब्बन की हिब्रू पांडुलिपियों का लैटिन में अनुवाद किया गया था और कई वर्षों बाद फ्रांसीसी विद्वान पीटर कोकिला (विद्वान)विद्वान) ने इसमें सुधार किया।[10][11] अनुवाद के कारण, टिब्बन, या प्रोफेटियस जुडेयस, जैसा कि वह लैटिन में जाना जाता था, खगोल विज्ञान में प्रभावशाली नाम बन गया था। उनका नया चतुर्भुज इस विचार पर आधारित था कि त्रिविमीय प्रक्षेपण जो समतलीय एस्ट्रोलैब को परिभाषित करता है, तब भी काम कर सकता है यदि एस्ट्रोलैब भागों को ही चतुर्थांश में मोड़ दिया जाए।[12] परिणाम ऐसा उपकरण था जो मानक एस्ट्रोलैब की तुलना में कहीं कंम उपयोग में आसान और अधिक वहनीय था। टिब्बन के काम की बहुत दूर तक पहुंच थी और उसने कोपरनिकस, क्रिस्टोफर की और इरास्मस रेनहोल्ड को प्रभावित किया; और उनकी पांडुलिपि को दांते एलघिएरी दांते की ईश्वरीय सुखान्तिकी में संदर्भित किया गया था।[13]

जैसे-जैसे चतुर्थांश छोटा होता गया और इस प्रकार अधिक वहनीय होता गया, मार्गदर्शन के लिए इसका मान जल्द ही अनुभूत किया जाने लगा। समुद्र में नेविगेट करने के लिए चतुर्भुज का पहला प्रलेखित उपयोग 1461 में डिओगो गोम्स द्वारा किया गया है।[14] नाविकों ने अपने अक्षांश का पता लगाने के लिए पोलारिस की ऊंचाई को मापना प्रारंभ किया है । चतुष्कोणों के इस आवेदन को सामान्यतः अरब नाविकों के लिए उत्तरदाई ठहराया जाता है जो अफ्रीका के पूर्वी तट पर व्यापार करते थे और अधिकांशतः भूमि की दृष्टि से बाहर यात्रा करते थे। इस तथ्य के कारण कि पोलारिस भूमध्य रेखा के दक्षिण में दिखाई नहीं देता है, जल्द ही निश्चित समय पर सूर्य की ऊंचाई लेना अधिक सामान्य हो गया है।

1618 में अंग्रेजी गणितज्ञ एडमंड गुंटर ने चतुर्थांश को आविष्कार के साथ अनुकूलित किया जिसे गुंटर चतुर्थांश के रूप में जाना जाने लगा है।[15] यह जेब के आकार का चतुर्भुज क्रांतिकारी था क्योंकि यह कटिबंधों, भूमध्य रेखा, क्षितिज और ग्रहण के अनुमानों के साथ खुदा हुआ था। सही तालिकाओं के साथ, समय, तिथि, दिन या रात की लंबाई, सूर्योदय और सूर्यास्त का समय और मध्याह्न का पता लगाने के लिए चतुर्भुज का उपयोग किया जा सकता है। गंटर चतुर्भुज अत्यंत उपयोगी था किन्तु इसकी कमियां थीं; तराजू केवल निश्चित अक्षांश पर प्रयुक्त होते हैं इसलिए उपकरण का उपयोग समुद्र में सीमित था।

प्रकार

1598 में उरनिबोर्ग में टाइको ब्राहे के भित्ति चतुर्थांश का उत्कीर्णन, दो घड़ियों का चित्रण।

चतुर्भुज कई प्रकार के होते हैं:

  • भित्ति यंत्र, आकाशीय समन्वय प्रणाली या खगोलीय वस्तुओं की ऊंचाई को मापकर समय का निर्धारण करने के लिए उपयोग किया जाता है। टायको ब्राहे ने सबसे बड़े भित्ति चतुर्थांशों में से बनाया है। समय बताने के लिए वह चतुर्थांश के बगल में दो घड़ियां रखता था जिससे वह यंत्र की तरफ माप के संबंध में मिनट और सेकंड की पहचान कर सके।[16]
  • खगोलीय पिंडों के बीच कोणीय दूरियों को मापने के लिए उपयोग किए जाने वाले बड़े फ्रेम-आधारित उपकरण है।
  • ज्यामितीय चतुर्भुज सर्वेक्षण और मार्गदर्शन द्वारा उपयोग किया जाता है।
  • डेविस चतुर्भुज कॉम्पैक्ट, फ़्रेमयुक्त उपकरण है जिसका उपयोग नाविक किसी खगोलीय वस्तु की ऊंचाई मापने के लिए करते हैं।

उन्हें इस रूप में भी वर्गीकृत किया जा सकता है:[17]

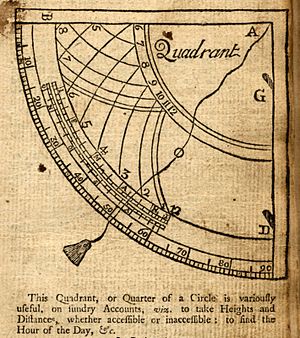
1744 के निर्देशात्मक पाठ में दर्शाए अनुसार लगभग 51.5° के अक्षांश के लिए होरेरी चतुर्थांश: दिन का समय खोजने के लिए: महीने के दिन पर ही धागा बिछाएं, तब तक इसे तब तक पकड़ें जब तक कि आप छोटे मनके या पिन-हेड को खिसका न दें [धागे के साथ] 12 बजे की रेखाओं में से पर आराम करने के लिए; फिर सूर्य को साइट जी से दूसरे स्थान पर डी पर चमकने दें, स्वतंत्रता पर लटका हुआ प्लमेट, बीड दिन के घंटे पर आराम करेगा।

*ऊंचाई - साहुल रेखा के साथ समतल चतुर्थांश, जिसका उपयोग किसी वस्तु की क्षैतिज समन्वय प्रणाली लेने के लिए किया जाता है।

  • गनर्स - तोप या मोर्टार की बंदूक बैरल के उन्नयन या अवसाद कोण को मापने के लिए तोपें द्वारा उपयोग किया जाने वाला प्रकार का क्लेनामिटर , दोनों उचित फायरिंग ऊंचाई को सत्यापित करने के लिए, और हथियार-से लगे अग्नि नियंत्रण उपकरणों के सही संरेखण को सत्यापित करने के लिए है।
  • गुंटर - समय निर्धारण के साथ-साथ दिन की लंबाई, जब सूर्य उदय और अस्त हो गया था, दिनांक, और भूमध्य रेखा का उपयोग संबंधित तालिकाओं के साथ-साथ चतुर्थांश के तराजू और वक्रों का उपयोग करने के लिए किया जाता है। इसका आविष्कार 1623 में एडमंड गुंटर द्वारा किया गया था। गुंटर का चतुर्भुज अधिक सरल था जिसने 17वीं और 18वीं शताब्दी में इसके व्यापक और लंबे समय तक उपयोग की अनुमति दी थी। गुंटर ने सुविधाजनक और व्यापक साधन बनाने के लिए अन्य चतुर्भुजों की मूलभूत विशेषताओं का विस्तार किया।[18] इसकी विशिष्ट विशेषता में उष्णकटिबंधीय, भूमध्य रेखा, ग्रहण और क्षितिज के अनुमान सम्मिलित थे।[15]*मुस्लिम - राजा ने चार प्रकार के चतुष्कोणों की पहचान की जो मुस्लिम खगोलविदों द्वारा निर्मित किए गए थे।[7] या ज्या चतुर्भुज (अरबी: रुबुल मुजय्यब) - जिसे साइनकाल चतुर्भुज के रूप में भी जाना जाता है - का उपयोग त्रिकोणमितीय समस्याओं को हल करने और खगोलीय टिप्पणियों को लेने के लिए किया गया था। यह 9वीं शताब्दी बगदाद में अल-ख्वारिज्मी द्वारा विकसित किया गया था और उन्नीसवीं शताब्दी तक प्रचलित था। इसकी पारिभाषिक विशेषता तरफ ग्राफ-पेपर जैसा ग्रिड है जो प्रत्येक अक्ष पर साठ सामान अंतरालों में विभाजित है और 90 डिग्री अंशांकित चाप से घिरा हुआ है। गणना के लिए, और साहुल बॉब के साथ मनका के साथ चतुर्भुज के शीर्ष पर रस्सी जुड़ी हुई थी। उन्हें कभी-कभी एस्ट्रॉलैब की पीठ पर भी खींचा जाता था।
  1. सार्वभौमिक (शक्काज़िया) चतुर्भुज - किसी भी अक्षांश के लिए खगोलीय समस्याओं को हल करने के लिए उपयोग किया जाता है: इन चतुर्भुजों में शक्काज़िया ग्रिड के या दो समूह थे और चौदहवीं शताब्दी में सीरिया में विकसित किए गए थे। इब्न अल-सरराज द्वारा बनाए गए एस्ट्रोलैब की तरह सार्वभौमिक चतुर्भुज के साथ कुछ एस्ट्रोलैब भी पीठ पर मुद्रित होते हैं।
  2. घोर चतुर्भुज - सूर्य के साथ समय खोजने के लिए प्रयोग किया जाता है: प्रश्नोत्तर चतुर्थांश का उपयोग या तो सामान या असमान (बारह से विभाजित दिन की लंबाई) घंटों में समय खोजने के लिए किया जा सकता है। मार्किंग के अलग-अलग समूह या तो सामान या असमान घंटों के लिए बनाए गए थे। समान घंटों में समय को मापने के लिए, प्रश्नोत्तर चतुर्थांश का उपयोग केवल विशिष्ट अक्षांश के लिए किया जा सकता है, जबकि असमान घंटों के लिए चतुर्थांश का उपयोग अनुमानित सूत्र के आधार पर कहीं भी किया जा सकता है। चतुर्भुज के किनारे को सूर्य के साथ संरेखित किया जाना था, और बार संरेखित होने पर, चतुर्भुज के केंद्र से जुड़ी साहुल रेखा पर मनका दिन का समय दिखाता था। यूरोपीय स्रोतों (इंग्लैंड के रिचर्ड द्वितीय) से उदाहरण दिनांक 1396 उपस्थित है।[19] 2013 में ज़ुतफेन (नीदरलैंड्स) के हंसियाटिक शहर में खुदाई के समय सबसे पुराना हॉरी क्वाड्रेंट पाया गया था, दिनांक सीए है। 1300, और जुत्फेन में स्थानीय स्टेडेलिज्क संग्रहालय में है।[20][21] या द एस्ट्रोलैब/एल्मुकांटार वृत्तखंड - एस्ट्रोलैब से विकसित क्वाड्रेंट: इस क्वाड्रेंट को विशिष्ट एस्ट्रोलबे प्लेट के आधे भाग के साथ चिह्नित किया गया था क्योंकि एस्ट्रोलबे प्लेट सममित हैं। दूसरे छोर पर मनके के साथ चतुर्भुज के केंद्र से जुड़ी रस्सी को खगोलीय पिंड (सूर्य या तारा) की स्थिति का प्रतिनिधित्व करने के लिए स्थानांतरित किया गया था। उपरोक्त के लिए क्रांतिवृत्त और तारा स्थिति को चतुर्थांश पर चिह्नित किया गया था। यह ज्ञात नहीं है कि एस्ट्रोलबे क्वाड्रेंट का आविष्कार कब और कहां हुआ था, वर्तमान एस्ट्रोलबे वृत्तखंड या तो ओटोमन या मामलुक मूल के हैं, जबकि एस्ट्रोलबे वृत्तखंड पर बारहवीं शताब्दी के मिस्र और चौदहवीं शताब्दी के सीरियाई ग्रंथों की खोज की गई है। ये चतुर्भुज एस्ट्रोलैब्स के लिए बहुत लोकप्रिय विकल्प सिद्ध हुए थे।

ज्यामितीय चतुर्भुज

साहुल बॉब के साथ ज्यामितीय चतुर्भुज।

ज्यामितीय चतुर्भुज सामान्यतः लकड़ी या पीतल का चौथाई घेरा फलक होता है। सतह पर चिह्नों को कागज पर मुद्रित किया जा सकता है और लकड़ी पर चिपकाया जा सकता है या सीधे सतह पर चित्रित किया जा सकता है। पीतल के यंत्रों पर उनके निशान सीधे पीतल में अंकित होते थे।

समुद्री मार्गदर्शन के लिए, सबसे प्रारंभिक उदाहरण 1460 के आसपास पाए गए थे। वे डिग्री में ग्रेजुएशन (उपकरण) नहीं थे, किन्तु विक्षनरी पर सीधे लिखे गए सबसे आम गंतव्यों के अक्षांश थे: लिंब या व्युत्पत्ति 2। उपयोग में होने पर, नाविक नौकायन करेगा उत्तर या दक्षिण जब तक चतुर्थांश ने संकेत नहीं दिया कि वह गंतव्य के अक्षांश पर है, गंतव्य की दिशा में मुड़ें और निरंतर अक्षांश के पाठ्यक्रम को बनाए रखते हुए गंतव्य की ओर बढ़ें। 1480 के बाद, अधिक उपकरणों को डिग्री में स्नातक किए गए अंगों के साथ बनाया गया था।[22]

एक किनारे के साथ दो जगहें असलियत बना रही थीं। शीर्ष पर चाप के केंद्र से रेखा द्वारा सीधा लटना को निलंबित कर दिया गया था।

आकाशीय समन्वय प्रणाली को मापने के लिए या तारे की ऊँचाई, पर्यवेक्षक तारे को स्थलों के माध्यम से देखेगा और चतुर्भुज को पकड़ेगा जिससे उपकरण का तल लंबवत हो। प्लंब बॉब को लंबवत लटका दिया गया था और रेखा ने चाप के ग्रेजुएशन (उपकरण ) पर रीडिंग का संकेत दिया था। दूसरे व्यक्ति के लिए रीडिंग लेना असामान्य नहीं था, जबकि पहले व्यक्ति ने उपकरण को उचित स्थिति में देखने और पकड़ने पर ध्यान केंद्रित किया।

उपकरण की स्पष्टता उसके आकार से सीमित थी और प्रभाव से हवा या पर्यवेक्षक की गति प्लंब बॉब पर होगी। चलते जहाज के डेक पर नाविकों के लिए, इन सीमाओं को पार करना कठिनाई हो सकता है।

सौर अवलोकन

पश्च अवलोकन चतुर्भुज का आरेखण। इस उपकरण का उपयोग उपकरण पर छाया की स्थिति को देखकर सूर्य की ऊंचाई को मापने के लिए बैकस्टाफ के रूप में किया गया था।

इसकी ऊंचाई को मापने के लिए सूर्य में घूरने से बचने के लिए, नाविक अपने सामने उपकरण को सूरज के साथ अपनी तरफ रख सकते थे। सूर्य की ओर देखने वाले फलक की छाया नीचे दिखने वाले फलक पर पड़ने से, यंत्र को सूर्य के साथ संरेखित करना संभव हो गया। यह सुनिश्चित करने के लिए ध्यान रखना होगा कि सूर्य के केंद्र की ऊंचाई निर्धारित की गई थी। यह छाया में ऊपरी और निचले गर्भ की ऊंचाई का औसत करके किया जा सकता है।

पिछला प्रेक्षण चतुर्थांश

सूर्य की ऊँचाई का मापन करने के लिए, पश्च अवलोकन चतुर्भुज विकसित किया गया था।[22]

इस तरह के चतुर्भुज के साथ, पर्यवेक्षक क्षितिज फलक (बी) में भट्ठा के माध्यम से दृष्टि फलक (दाईं ओर की आकृति में सी) से क्षितिज को देखता है। यह सुनिश्चित करता है कि उपकरण स्तर था। प्रेक्षक नेछाया फलक (ए) को स्नातक स्तर पर स्थिति में स्थानांतरित कर दिया जिससे उसकी छाया क्षितिज वेन पर क्षितिज के स्तर के साथ मेल खाती दिखाई दे। यह कोण सूर्य का उत्थान था।

फ़्रेमयुक्त चतुर्भुज

खगोलीय मापन के लिए बड़े फ्रेम चतुर्भुज का उपयोग किया गया था, विशेष रूप से आकाशीय समन्वय प्रणाली का निर्धारण या खगोलीय वस्तु वस्तुओं की ऊंचाई। वे स्थायी प्रतिष्ठान हो सकते हैं, जैसे भित्ति यंत्र। छोटे चतुर्भुजों को स्थानांतरित किया जा सकता है। समान षष्ठक (खगोलीय) या फ़्रेमयुक्त षष्ठक की तरह, उन्हें ऊर्ध्वाधर स्तर में उपयोग किया जा सकता है या किसी भी स्तर के लिए समायोज्य बनाया जा सकता है।

जब कुरसी या अन्य माउंट पर समूह किया जाता है, तो उनका उपयोग किसी भी दो खगोलीय पिंडों के बीच कोणीय दूरी को मापने के लिए किया जा सकता है।

उनके निर्माण और उपयोग पर विवरण अनिवार्य रूप से षष्ठक (खगोलीय) या फ्रेमेड षष्ठक के समान हैं; विवरण के लिए उस लेख को देखें।

नौसेना: जहाजों के तोप पर ऊंचाई नापने के लिए उपयोग किया जाता है, लोडिंग के बाद दूरी को जज करने के लिए क्वाड्रेंट को प्रत्येक गन के ट्रूनियन पर रखा जाना था। जहाज के रोल के शीर्ष पर रीडिंग ली गई, बंदूक को समायोजित किया गया, और रोल के शीर्ष पर फिर से जाँच की गई, और वह अगली बंदूक तक चला गया, जब तक कि निकाली जाने वाली सभी तैयार नहीं हो गईं। जहाज के गनर को सूचित किया गया, जिसने बदले में कप्तान को सूचित किया...आप तैयार होने पर फायर कर सकते हैं...अगले उच्च रोल पर, तोप दागी जाएगी।

अधिक आधुनिक अनुप्रयोगों में, चतुर्भुज ट्रूनियन रिंग या बड़ी नौसैनिक बंदूक से जुड़ा होता है जिससे इसे जहाज के डेक पर वेल्डेड बेंचमार्क के साथ संरेखित किया जा सके। यह सुनिश्चित करने के लिए किया जाता है कि बंदूक की फायरिंग ने डेक को विकृत नहीं किया है। माउंट गनहाउस या बुर्ज पर सपाट सतह को बेंचमार्क के विपरीत भी जांचा जाता है, साथ ही, यह सुनिश्चित करने के लिए कि बड़े बियरिंग और/या बियरिंग रेस बंदूक को "कैलिब्रेट" करने के लिए नहीं बदले हैं।


जाता है कि बंदूक की फायरिंग ने डेक को विकृत नहीं किया है। माउंट गनहाउस या बुर्ज पर सपाट सतह को बेंचमार्क के विपरीत भी जांचा जाता है, साथ ही, यह सुनि

अनुकूलन

मध्य युग के समय , निर्माताओं ने अधिकांशतः उस व्यक्ति को प्रभावित करने के लिए अनुकूलन जोड़ा जिसके लिए चतुर्भुज का इरादा था। उपकरण पर बड़े, अप्रयुक्त स्थानों में, सिगिल या बैज अधिकांशतः महत्वपूर्ण व्यक्ति या मालिक की निष्ठा के स्वामित्व को दर्शाने के लिए जोड़ा जाता है।[23]

यह भी देखें

  • डेविस चतुर्थांश
  • खगोलीय उपकरणों की सूची
  • भित्ति यंत्र

संदर्भ

  1. ↑ 1.0 1.1 G. V. Raghava Rau (1949). स्वर्ग का शास्त्र. Ananda Press. p. 8.
  2. ↑ 2.0 2.1 University of Calcutta (1924). Journal of the Department of Science Volume 6. University of Calcutta. Dept. of Science. p. 57.
  3. ↑ King, Henry C. (2003) [1955]. टेलीस्कोप का इतिहास. Dover Publications. ISBN 978-0-486-43265-6.
  4. ↑ Witzel 2019, p. 11: "Incidentally, the Indo-Aryan loanwords in Mitanni confirm the date of the Rig Veda for ca. 1200–1000 BCE. The Rig Veda is a late Bronze age text, thus from before 1000 BCE. However, the Mitanni words have a form of Indo-Aryan that is slightly older than that ... Clearly the Rig Veda cannot be older than ca. 1400, and taking into account a period needed for linguistic change, it may not be much older than ca. 1200 BCE."
  5. ↑ Ackermann, Silke; Van Gent, Robert. "वृत्त का चतुर्थ भाग". Epact: Scientific Instruments of Medieval and Renaissance Europe. Museum of the History of Science.
  6. ↑ Cite error: Invalid <ref> tag; no text was provided for refs named Quadrant
  7. ↑ 7.0 7.1 King, David A. (1987). इस्लामी खगोलीय उपकरण. London: Variorum Reprints. ISBN 0860782018.
  8. ↑ O'Connor, J.J. "याकूब बिन मुशीर बिन तैयबौन". Tibbon Biography. University of St. Andrews.
  9. ↑ "द एस्ट्रोलैब क्वाड्रंट". Astrolabes. Archived from the original on 2018-07-21.
  10. ↑ "डसिया के पीटर फिलोमेना, जिन्हें पीटर डैकस, पीटर डैनस, पीटर नाइटिंगेल के नाम से भी जाना जाता है". Encyclopedia.com (in English). Complete Dictionary of Scientific Biography.
  11. ↑ Lindberg, David C., ed. (1988). मध्य युग में विज्ञान. Chicago, Ill. [u.a.]: Univ. of Chicago Press. ISBN 0226482332.
  12. ↑ Pedersen, Olaf (1993). Early physics and astronomy : a historical introduction. Cambridge: Cambridge University Press. ISBN 0521408997.
  13. ↑ Cite error: Invalid <ref> tag; no text was provided for refs named Jacob ben Machir ibn Tibbon
  14. ↑ "वृत्त का चतुर्थ भाग". Department of Mathematics. University of Singapore. Archived from the original on 2018-10-06.
  15. ↑ 15.0 15.1 "गुंटर चतुर्भुज". National Museum of American History. Smithsonian. Retrieved April 25, 2018.
  16. ↑ Dreyer, John (2014). टाइको ब्राहे. Cambridge University Press. ISBN 978-1-108-06871-0.
  17. ↑ Turner, Gerard L'E. (1980). प्राचीन वैज्ञानिक उपकरण. Blandford Press Ltd. ISBN 0-7137-1068-3.
  18. ↑ Davis, John (September 2011). "A Medieval Gunter's Quadrant?" (PDF). British Sundial Society Bulletin. 23 (iii). Retrieved April 25, 2018.
  19. ↑ Clayton Bloom (9 November 2011). "14th century timepiece unearthed in Qld farm shed". ABC News Online. Retrieved 10 November 2011.
  20. ↑ Davis, John (March 2014). "The Zutphen Quadrant – A Very Early Equal-Hour Instrument Excavated in The Netherlands" (PDF). British Sundial Society Bulletin. 26 (i): 36–42. Retrieved May 31, 2018.
  21. ↑ Fermin, B.; Kastelein, D. (2013). जूटफेन चतुर्थांश। जूटफेन में हौटमार्क पर रिंगवालबर्ग की खाई में पुरातत्व अनुसंधान [The Zutphen Quadrant. Archaeological research in the moat of the ringwalburg on the Houtmarkt in Zutphen] (in Nederlands). Zutphen: Zutphense Archaeological Publications 80. doi:10.17026/dans-xyp-9pzw.
  22. ↑ 22.0 22.1 May, William Edward (1973). समुद्री नेविगेशन का इतिहास. Henley-on-Thames, Oxfordshire: G. T. Foulis & Co. Ltd. ISBN 0-85429-143-1.
  23. ↑ Silke Ackermann & John Cherry (1999). "रिचर्ड द्वितीय, जॉन हॉलैंड और तीन मध्यकालीन चतुर्भुज". Annals of Science. 56 (1): 3–23. doi:10.1080/000337999296508.
  • Maurice Daumas, Scientific Instruments of the Seventeenth and Eighteenth Centuries and Their Makers, Portman Books, London 1989 ISBN 978-0-7134-0727-3


बाहरी संबंध

Wikimedia Commons has media related to Quadrants (instrument).
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=चतुर्थांश_(साधन)&oldid=149022’