हाइपर आवेश (हाइपरचार्ज)

This article is about हैड्रोन की एक क्वांटम संख्या. For इलेक्ट्रोविक सिद्धांत में समान संख्या, see अशक्त हाइपरचार्ज.

कण भौतिकी में, एक उप-परमाणु कण का हाइपरआवेश (हाइपरॉन और आवेश (भौतिकी) का एक पोर्टमैंटो) Y एक क्वांटम संख्या है जो शसक्त अंतःक्रिया के तहत संरक्षित है। हाइपरआवेश की अवधारणा एक एकल आवेश (भौतिकी) प्रदान करती है जो समभारिक प्रचक्रण , विद्युत आवेश और स्वाद (कण भौतिकी) के गुणों के लिए उत्तरदाई है। हाइपरआवेश हैड्रान को वर्गीकृत करने के लिए उपयोगी है; समान रूप से नामित अशक्त हाइपरआवेश की इलेक्ट्रोवीक परस्पर क्रिया में एक समान भूमिका होती है।

परिभाषा

हाइपरआवेश आइसोस्पिन I₃ के साथ हैड्रॉन के एसयू (3) मॉडल के दो क्वांटम नंबरों में से एक है। अकेले आइसोस्पिन दो क्वार्क स्वादों के लिए पर्याप्त था - अर्थात्
u
और
d
- जबकि वर्तमान में क्वार्क के 6 स्वाद ज्ञात हैं।

SU(3) वजन आरेख (नीचे देखें) 2 आयामी हैं, जिसमें निर्देशांक दो क्वांटम नंबरों को संदर्भित करते हैं: I₃ (जिसे I_z के रूप में भी जाना जाता है) जो आइसोस्पिन का z घटक है, और Y, जो हाइपरआवेश (विचित्रता का योग) है (विचित्रता S, आकर्षण C, बॉटमनेस B′', टॉपनेस T′', और बैरियन नंबर B का योग) है । गणितीय रूप से हाइपरआवेश है

$Y=B+S+C+B'+T'~.$

शसक्त परस्पर क्रिया हाइपरआवेश (और अशक्त हाइपरआवेश) को बचाते हैं, किंतु अशक्त परस्पर क्रिया नहीं करते हैं।

इलेक्ट्रिक आवेश और आइसोस्पिन के साथ संबंध

Main article: गेल-मान-निशिजिमा सूत्र

गेल-मान-निशिजीमा सूत्र आइसोस्पिन और विद्युत आवेश से संबंधित है

$Q=I_{3}+{\tfrac {1}{2}}Y,$

जहां I₃ आइसोस्पिन का तीसरा घटक है और Q कण का आवेश है।

आइसोस्पिन कणों के गुणक बनाता है जिसका औसत आवेश हाइपरआवेश से संबंधित होता है:

$Y=2{\bar {Q}}.$

चूंकि बहुविकल्पी के सभी सदस्यों के लिए हाइपरआवेश समान है और I₃ मानों का औसत 0 है।

हाइपरआवेश के संबंध में SU(3) मॉडल

SU(2) मॉडल में एक क्वांटम संख्या J की विशेषता वाले गुणक हैं, जो कि कुल कोणीय गति है। प्रत्येक बहुविकल्पी में 2J + 1 सम्मिलित हैं जो J_z के समान दूरी वाले मूल्यों के साथ होते हैं, जो परमाणु स्पेक्ट्रा और आइसोस्पिन में देखी गई एक सममित व्यवस्था का बनाते हैं। यह अवलोकन को औपचारिक रूप देता है कि कुछ शसक्त बैरोन क्षय नहीं देखे गए, जिससे बड़े मापदंड पर विचित्रता और
Ω⁻
बेरियन के आवेश की पूर्वानुमान की जा सकती है।

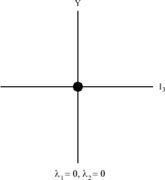
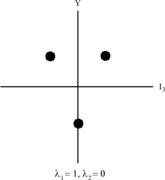
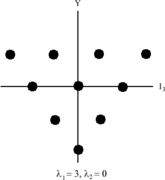
SU(3) में SU(2) बहुविकल्पी वाले बहुगुणक हैं। SU(3) को अब अपने सभी उप-स्तरों को निर्दिष्ट करने के लिए दो संख्याओं की आवश्यकता है जिन्हें λ₁ और λ₂ द्वारा दर्शाया गया है॥

(λ₁ + 1) षट्भुज के शीर्ष भाग में बिंदुओं की संख्या निर्दिष्ट करता है जबकि (λ₂ + 1) नीचे की तरफ अंकों की संख्या निर्दिष्ट करता है।

• 

  SU(3) singlet weight diagram, where Y is hypercharge and I₃ is the third component of isospin.

• 

  SU(3) triplet weight diagram

• 

  SU(3) septet, octet, and nonet weight diagram Note similarity with both charts on the right. The number used to describe the weight diagram depends on whether the particle(s) occupying the center of the diagram have one, two, or three distinct names.

• 

  Mesons of spin 0 form a nonet. K: kaon, π: pion, η: eta meson.

• 

  The octet of light spin-1/2 baryons described in SU(3). n: neutron, p: proton, Λ: Lambda baryon, Σ: Sigma baryon, Ξ: Xi baryon.

• 

  SU(3) decuplet weight diagram Note similarity with chart on the right.

• 

  A combination of three up, down or strange quarks with a total spin of 3/2 form the so-called baryon decuplet. The lower six are hyperons. S: strangeness, Q: electric charge.

उदाहरण

• न्यूक्लियॉन समूह ( Q = +1 वाले प्रोटॉन Q = 0 वाले न्यूट्रॉन ) का औसत ++1/2 होता है , इसलिए उन दोनों में हाइपरआवेश Y = 1 होता है (चूंकि बैरियन संख्या B = +1 ,, और S = C = B′ = T′ = 0)। गेल-मान-निशिजीमा सूत्र से हम जानते हैं कि प्रोटॉन का समस्थानिक I₃ = ++1/2 , होता है, जबकि न्यूट्रॉन का I₃ = −+1/2 . होता है।
• यह क्वार्क के लिए भी काम करता है: अप क्वार्क के लिए, ++2/3 के आवेश के साथ, और ++1/2 के I₃ के साथ, हम 1/3 का हाइपरआवेश घटाते हैं, हम ++1/3 का हाइपरआवेश निकालते हैं।
• एक विचित्र क्वार्क के लिए, विद्युत आवेश −+1/3 , बेरिऑन संख्या ++1/3 और विचित्रता −1 के साथ, हमें हाइपरआवेश Y = −+2/3 , प्राप्त होता है, इसलिए हम यह निष्कर्ष निकालते हैं कि I₃ = 0 . इसका अर्थ है कि एक विचित्र क्वार्क अपने स्वयं के एक आइसोस्पिन सिंगलेट बनाता है (वही चार्म बॉटम और टॉप क्वार्क के साथ होता है), जबकि ऊपर और नीचे एक आइसोस्पिन डबलट का गठन होता है।

व्यावहारिक अप्रचलन

हाइपरआवेश 1960 के दशक में कण चिड़ियाघर में कणों के समूहों को व्यवस्थित करने और उनके देखे गए परिवर्तनों के आधार पर तदर्थ संरक्षण नियमो को विकसित करने के लिए विकसित एक अवधारणा थी। क्वार्क मॉडल के आगमन के साथ, अब यह स्पष्ट हो गया है कि प्रबल हाइपरआवेश, Y, ऊपर क्वार्क की संख्याओं का निम्न संयोजन है (n_u), डाउन क्वार्क (n_d), विचित्र क्वार्क  (n_s), आकर्षण क्वार्क  (n_c), शीर्ष क्वार्क  (n_t) और निचला क्वार्क  (n_b) की संख्याओं का निम्न संयोजन है :

$Y={\tfrac {1}{3}}n_{\textrm {u}}+{\tfrac {1}{3}}n_{\textrm {d}}-{\tfrac {2}{3}}n_{\textrm {s}}+{\tfrac {4}{3}}n_{\textrm {c}}-{\tfrac {2}{3}}n_{\textrm {b}}+{\tfrac {4}{3}}n_{\textrm {t}}~.$

हैड्रॉन परस्पर क्रिया के आधुनिक विवरणों में, फेनमैन आरेखों को आकर्षित करना अधिक स्पष्ट हो गया है जो शसक्त हाइपरआवेश क्वांटम संख्याओं को गिनने के बजाय अलग-अलग घटक क्वार्क (जो संरक्षित हैं) के माध्यम से परस्पर क्रिया करने वाले बेरोन और मेसन की रचना करते हैं। अशक्त हाइपरआवेश, हालांकि, इलेक्ट्रोवीक परस्पर क्रिया को समझने का एक अनिवार्य हिस्सा बना हुआ है।

इलेक्ट्रोवीक परस्पर क्रिया को समझने का एक अनिवार्य हिस्सा बना हुआ है।

संदर्भ

• Semat, Henry; Albright, John R. (1984). Introduction to Atomic and Nuclear Physics. Chapman and Hall. ISBN 978-0-412-15670-0.