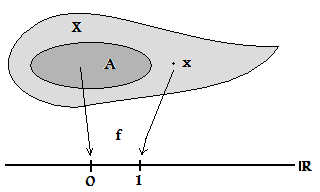
टायचोनॉफ स्पेस
| Separation axioms in topological spaces | |
|---|---|
| Kolmogorov classification | |
| T0 | (Kolmogorov) |
| T1 | (Fréchet) |
| T2 | (Hausdorff) |
| T2½ | (Urysohn) |
| completely T2 | (completely Hausdorff) |
| T3 | (regular Hausdorff) |
| T3½ | (Tychonoff) |
| T4 | (normal Hausdorff) |
| T5 | (completely normal Hausdorff) |
| T6 | (perfectly normal Hausdorff) |
टोपोलॉजी और गणित की संबंधित शाखाओं में, टाइकोनॉफ़ स्पेस और पूरी तरह से नियमित स्पेस टोपोलॉजिकल स्पेस के प्रकार हैं। ये स्थितियाँ पृथक्करण अभिगृहीतों के उदाहरण हैं। एक टाइकोनॉफ़ स्थान किसी भी पूरी तरह से नियमित स्थान को संदर्भित करता है जो हॉसडॉर्फ स्थान भी है; वहाँ पूरी तरह से नियमित स्थान मौजूद हैं जो टाइकोनॉफ़ नहीं हैं (अर्थात हौसडॉर्फ नहीं)।
Tychonoff रिक्त स्थान का नाम एंड्री निकोलाइविच तिखोनॉफ के नाम पर रखा गया है, जिनके रूसी भाषा के नाम (Тихонов) को विभिन्न रूप से Tychonov, Tikhonov, Tihonov, Tichonov, आदि के रूप में प्रस्तुत किया गया है, जिन्होंने 1930 में हौसडॉर्फ रिक्त स्थान की पैथोलॉजिकल स्थिति से बचने के लिए उनका परिचय दिया था, जिसका एकमात्र निरंतर वास्तविक- मूल्यवान कार्य निरंतर मानचित्र हैं।[1]
परिभाषाएँ
एक टोपोलॉजिकल स्पेस कहा जाता हैcompletely regular यदि बिंदुओं को बंद सेटों से (बाध्य) निरंतर वास्तविक-मूल्यवान कार्यों के माध्यम से अलग किया जा सकता है। तकनीकी शब्दों में इसका अर्थ है: किसी भी बंद सेट के लिए और कोई बिंदु (ज्यामिति) अस्तित्वगत मात्रा का ठहराव एक वास्तविक रेखा | वास्तविक-मूल्यवान निरंतर कार्य (टोपोलॉजी) ऐसा है कि और (समतुल्य रूप से इसके बजाय कोई भी दो मान चुन सकते हैं और और यहां तक कि मांग करते हैं एक बाध्य कार्य हो।)
एक टोपोलॉजिकल स्पेस को कहा जाता हैTychonoff space (वैकल्पिक रूप से:T3½ space, या Tπ space, या completely T3 space) यदि यह पूरी तरह से नियमित हौसडॉर्फ स्थान है।
टिप्पणी। पूरी तरह से नियमित रिक्त स्थान और टाइकोनॉफ़ रिक्त स्थान कोलमोगोरोव तुल्यता की धारणा से संबंधित हैं। एक टोपोलॉजिकल स्पेस टायकोनॉफ़ है अगर और केवल अगर यह पूरी तरह से नियमित और कोलमोगोरोव स्पेस दोनों है। टी0. दूसरी ओर, एक स्थान पूरी तरह से नियमित है अगर और केवल अगर उसका कोलमोगोरोव भागफल टाइकोनॉफ़ है।
नामकरण परंपराएं
जब पूरी तरह से नियमित और टी-एक्सिओम्स शब्द की बात आती है तो गणितीय साहित्य में विभिन्न परंपराएं लागू होती हैं। इस खंड की परिभाषाएँ विशिष्ट आधुनिक उपयोग में हैं। हालाँकि, कुछ लेखक दो प्रकार के शब्दों के अर्थ बदल देते हैं, या सभी शब्दों का परस्पर उपयोग करते हैं। विकिपीडिया में, पूरी तरह से नियमित और टाइकोनॉफ़ शब्दों का स्वतंत्र रूप से उपयोग किया जाता है और आमतौर पर टी-नोटेशन से बचा जाता है। मानक साहित्य में, इस प्रकार सावधानी बरतने की सलाह दी जाती है, यह पता लगाने के लिए कि लेखक किन परिभाषाओं का उपयोग कर रहा है। इस मुद्दे पर अधिक जानकारी के लिए, पृथक्करण अभिगृहीतों का इतिहास देखें।
उदाहरण और प्रति उदाहरण
गणितीय विश्लेषण में अध्ययन किया गया लगभग हर टोपोलॉजिकल स्पेस टाइकोनॉफ़ है, या कम से कम पूरी तरह से नियमित है। उदाहरण के लिए, मानक यूक्लिडियन अंतरिक्ष के तहत वास्तविक रेखा टाइकोनॉफ़ है। अन्य उदाहरणों में शामिल हैं:
- प्रत्येक मीट्रिक स्थान टाइकोनॉफ़ है; हर स्यूडोमेट्रिक स्पेस पूरी तरह से नियमित है।
- प्रत्येक स्थानीय रूप से कॉम्पैक्ट नियमित स्थान पूरी तरह से नियमित है, और इसलिए प्रत्येक स्थानीय रूप से कॉम्पैक्ट हौसडॉर्फ स्थान टाइकोनॉफ़ है।
- विशेष रूप से, प्रत्येक टोपोलॉजिकल मैनिफोल्ड टाइकोनॉफ़ है।
- आदेश टोपोलॉजी के साथ हर पूरी तरह से ऑर्डर किया गया सेट टाइकोनॉफ़ है।
- प्रत्येक सांस्थितिक समूह पूर्णतः नियमित होता है।
- मेट्रिक स्पेस और टोपोलॉजिकल समूह दोनों का सामान्यीकरण करते हुए, हर एक समान स्थान पूरी तरह से नियमित है। इसका विलोम भी सत्य है: प्रत्येक पूर्णतः नियमित स्थान एकरूपता योग्य होता है।
- हर सीडब्ल्यू कॉम्प्लेक्स टाइकोनॉफ है।
- प्रत्येक सामान्य स्थान नियमित स्थान पूरी तरह से नियमित है, और प्रत्येक सामान्य हौसडॉर्फ स्थान टाइकोनॉफ़ है।
- नीमेत्ज़की विमान टाइकोनॉफ़ अंतरिक्ष का एक उदाहरण है जो सामान्य स्थान नहीं है।
गुण
संरक्षण
प्रारंभिक टोपोलॉजी के संबंध में पूर्ण नियमितता और टाइकोनॉफ संपत्ति अच्छी तरह से व्यवहार की जाती है। विशेष रूप से, मनमाना प्रारंभिक टोपोलॉजी लेकर पूर्ण नियमितता को संरक्षित किया जाता है और टाइकोनॉफ संपत्ति को बिंदु-पृथक्करण प्रारंभिक टोपोलॉजी लेकर संरक्षित किया जाता है। यह इस प्रकार है कि:
- पूरी तरह से नियमित या टाइकोनॉफ स्पेस के हर सबस्पेस (टोपोलॉजी) में एक ही संपत्ति होती है।
- एक गैर-खाली उत्पाद स्थान पूरी तरह से नियमित (क्रमशः टाइकोनॉफ़) होता है यदि और केवल यदि प्रत्येक कारक स्थान पूरी तरह से नियमित (क्रमशः टाइकोनॉफ़) हो।
सभी अलगाव सिद्धांतों की तरह, अंतिम टोपोलॉजी लेने से पूर्ण नियमितता संरक्षित नहीं होती है। विशेष रूप से, पूरी तरह से नियमित रिक्त स्थान के भागफल स्थान (टोपोलॉजी) को नियमित स्थान नहीं होना चाहिए। टाइकोनॉफ़ रिक्त स्थान के भागफलों को हॉसडॉर्फ स्थान की भी आवश्यकता नहीं है, जिसमें एक प्राथमिक प्रत्युत्तर उदाहरण दो मूल के साथ रेखा है। मूर विमान के बंद भागफल हैं जो प्रति उदाहरण प्रदान करते हैं।
वास्तविक-मूल्यवान निरंतर कार्य
किसी भी टोपोलॉजिकल स्पेस के लिए होने देना वास्तविक-मूल्यवान सतत कार्य (टोपोलॉजी) के परिवार को निरूपित करें और जाने परिबद्ध फलन वास्तविक-मूल्यवान सतत फलन का सबसेट हो।
पूरी तरह से नियमित रिक्त स्थान को इस तथ्य से चित्रित किया जा सकता है कि उनकी टोपोलॉजी पूरी तरह से निर्धारित होती है या विशेष रूप से:
- एक स्थान पूरी तरह से नियमित है अगर और केवल अगर इसके द्वारा प्रेरित प्रारंभिक टोपोलॉजी है या
- एक स्थान पूरी तरह से नियमित है अगर और केवल अगर प्रत्येक बंद सेट को शून्य सेट के परिवार के चौराहे के रूप में लिखा जा सकता है (यानी शून्य सेट के बंद सेट के लिए आधार बनाते हैं ).
- एक स्थान पूरी तरह से नियमित है अगर और केवल अगर कोज़ीरो सेट करता है की टोपोलॉजी के लिए एक आधार (टोपोलॉजी) बनाते हैं
एक मनमाना सामयिक स्थान दिया गया के साथ पूरी तरह से नियमित स्थान को जोड़ने का एक सार्वभौमिक तरीका है बता दें कि ρ प्रारंभिक टोपोलॉजी है प्रेरक या, समतुल्य, कोज़ीरो सेट के आधार पर उत्पन्न टोपोलॉजी तब ρ बेहतरीन टोपोलॉजी होगी, जिस पर पूरी तरह से नियमित टोपोलॉजी होगी वह इससे मोटा है यह निर्माण इस अर्थ में सार्वभौमिक संपत्ति है कि कोई भी निरंतर कार्य करता है
कोई यह दिखा सकता है उपरोक्त निर्माण में ताकि छल्ले और आम तौर पर केवल पूरी तरह से नियमित रिक्त स्थान के लिए अध्ययन किया जाता है रियलकॉम्पैक्ट स्पेस टाइकोनॉफ़ स्पेस की श्रेणी रिंगों की श्रेणी के समकक्ष नहीं है (कहाँ realcompact है) नक्शे के रूप में रिंग होमोमोर्फिज्म के साथ। उदाहरण के लिए कोई पुनर्निर्माण कर सकता है से कब (वास्तविक) कॉम्पैक्ट है। इसलिए इन छल्लों का बीजगणितीय सिद्धांत गहन अध्ययन का विषय है। छल्ले के इस वर्ग का एक विशाल सामान्यीकरण जो अभी भी टाइकोनॉफ रिक्त स्थान के कई गुणों जैसा दिखता है, लेकिन वास्तविक बीजगणितीय ज्यामिति में भी लागू होता है, वास्तविक बंद छल्ले का वर्ग है।
एम्बेडिंग
Tychonoff रिक्त स्थान ठीक वे स्थान हैं जो कॉम्पैक्ट हौसडॉर्फ स्पेस स्थान में टोपोलॉजिकल एम्बेडिंग हो सकते हैं। अधिक सटीक रूप से, प्रत्येक टाइकोनॉफ़ स्थान के लिए एक कॉम्पैक्ट हौसडॉर्फ स्थान मौजूद है ऐसा है कि की एक उपसमष्टि के लिए होमियोमॉर्फिक है वास्तव में, कोई हमेशा चुन सकता है टाइकोनॉफ क्यूब होना (अर्थात इकाई अंतराल का संभवतः अनंत उत्पाद)। टाइकोनॉफ के प्रमेय के परिणामस्वरूप प्रत्येक टाइकोनॉफ क्यूब कॉम्पैक्ट हॉसडॉर्फ है। चूंकि कॉम्पैक्ट हौसडॉर्फ अंतरिक्ष के प्रत्येक उप-स्थान टाइकोनॉफ के पास है:
- एक टोपोलॉजिकल स्पेस टाइकोनॉफ़ है अगर और केवल अगर इसे टाइकोनॉफ़ क्यूब में एम्बेड किया जा सकता है।
संघनन
विशेष रूप से रुचि वे एम्बेडिंग हैं जहां की छवि में घना उपसमुच्चय है इन्हें हॉसडॉर्फ संघनन (गणित)गणित) कहा जाता है टाइकोनॉफ स्पेस के किसी भी एम्बेडिंग को देखते हुए एक कॉम्पैक्ट हौसडॉर्फ स्पेस में की छवि का समापन (टोपोलॉजी)। में का संघनन है उसी 1930 के लेख में जहां टाइकोनॉफ़ ने पूरी तरह से नियमित रिक्त स्थान को परिभाषित किया था, उन्होंने यह भी साबित किया कि प्रत्येक टाइकोनॉफ़ स्पेस में हौसडॉर्फ कॉम्पेक्टिफिकेशन होता है।[2]
उन हॉसडॉर्फ कॉम्पैक्टिफिकेशन में, एक अनोखा सबसे सामान्य है, स्टोन-चेक कॉम्पेक्टिफिकेशन यह सार्वभौमिक संपत्ति की विशेषता है, जिसे एक निरंतर नक्शा दिया गया है से किसी अन्य कॉम्पैक्ट हौसडॉर्फ स्पेस के लिए एक अनोखा (गणित) निरंतर नक्शा है जो फैलता है इस अर्थ में कि की संरचना (कार्य) है और
समान संरचना
पूर्ण नियमितता एक सामयिक स्थान पर समान संरचनाओं के अस्तित्व के लिए आवश्यक शर्त है। दूसरे शब्दों में, प्रत्येक समान स्थान में एक पूरी तरह से नियमित टोपोलॉजी और प्रत्येक पूरी तरह से नियमित स्थान होता है एकरूप करने योग्य है। एक टोपोलॉजिकल स्पेस एक अलग समान संरचना को स्वीकार करता है यदि और केवल अगर यह टाइकोनॉफ़ है।
पूरी तरह से नियमित स्थान दिया गया आमतौर पर एक से अधिक एकरूपता होती है की टोपोलॉजी के अनुकूल है हालाँकि, हमेशा एक बेहतरीन संगत एकरूपता होगी, जिसे फ़ाइन एकरूपता कहा जाता है अगर Tychonoff है, तो समान संरचना को चुना जा सकता है एक समान स्थान का समापन (टोपोलॉजी) हो जाता है
यह भी देखें
उद्धरण
- ↑ Narici & Beckenstein 2011, p. 240.
- ↑ Narici & Beckenstein 2011, pp. 225–273.
ग्रन्थसूची
- Gillman, Leonard; Jerison, Meyer (1960). Rings of continuous functions. Graduate Texts in Mathematics, No. 43 (Dover reprint ed.). NY: Springer-Verlag. p. xiii. ISBN 978-048681688-3.
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Willard, Stephen (1970). General Topology (Dover reprint ed.). Reading, Massachusetts: Addison-Wesley Publishing Company. ISBN 0-486-43479-6.