संघनित पदार्थ भौतिकी में, लाफलिन वेवफंक्शन [1] एन्सैट्ज है, जिसे रॉबर्ट लाफलिन द्वारा एक समान जेलियम पृष्ठभूमि की उपस्थिति में एक समान पृष्ठभूमि चुंबकीय क्षेत्र में रखी गई दो-आयामी इलेक्ट्रॉन गैस की जमीनी स्थिति के लिए प्रस्तावित किया गया है। निम्नतम लन्दौ स्तर का भरण कारक (क्वांटम हॉल प्रभाव)  है जहाँ n विषम धनात्मक पूर्णांक है। इसका निर्माण
है जहाँ n विषम धनात्मक पूर्णांक है। इसका निर्माण  भिन्नात्मक क्वांटम हॉल प्रभाव के अवलोकन की व्याख्या करने के लिए किया गया था और अतिरिक्त
भिन्नात्मक क्वांटम हॉल प्रभाव के अवलोकन की व्याख्या करने के लिए किया गया था और अतिरिक्त  अवस्थाओं के साथ-साथ भिन्नात्मक विद्युत आवेश
अवस्थाओं के साथ-साथ भिन्नात्मक विद्युत आवेश  के साथ क्वासिपार्टिकल उद्दीपन के अस्तित्व की भविष्यवाणी की गई थी, दोनों बाद में प्रायोगिक तौर पर देखे गए थे। लाफलिन को इस खोज के लिए 1998 में भौतिकी के नोबेल पुरस्कार का एक तिहाई हिस्सा मिला था। ट्रायल वेवफंक्शन होने के नाते, यह सटीक नहीं है, लेकिन गुणात्मक रूप से, यह सटीक समाधान की कई विशेषताओं को पुन: पेश करता है और मात्रात्मक रूप से, छोटे प्रणाली के लिए सटीक जमीनी स्थिति के साथ इसका बहुत अधिक अतिव्यापन होता है।
के साथ क्वासिपार्टिकल उद्दीपन के अस्तित्व की भविष्यवाणी की गई थी, दोनों बाद में प्रायोगिक तौर पर देखे गए थे। लाफलिन को इस खोज के लिए 1998 में भौतिकी के नोबेल पुरस्कार का एक तिहाई हिस्सा मिला था। ट्रायल वेवफंक्शन होने के नाते, यह सटीक नहीं है, लेकिन गुणात्मक रूप से, यह सटीक समाधान की कई विशेषताओं को पुन: पेश करता है और मात्रात्मक रूप से, छोटे प्रणाली के लिए सटीक जमीनी स्थिति के साथ इसका बहुत अधिक अतिव्यापन होता है।
यदि हम एक शून्य क्रम सन्निकटन के रूप में इलेक्ट्रॉनों के बीच जेलियम और आपसी कूलम्ब प्रतिकर्षण को अनदेखा करते हैं, तो हमारे पास एक असीम रूप से निम्नतम लैंडौ स्तर (LLL) है और 1/n के भरण कारक के साथ, हम उम्मीद करेंगे कि सभी इलेक्ट्रॉन LLL में स्थित होंगे। अन्योन्यक्रियाओं को चालू करते हुए, हम अनुमान लगा सकते हैं कि सभी इलेक्ट्रॉन LLL में हैं। यदि  सबसे कम कक्षीय कोणीय संवेग के साथ LLL अवस्था का एकल कण तरंग है, तो मल्टीपार्टिकल वेवफंक्शन के लिए लाफलिन एनाट्ज़ है।
सबसे कम कक्षीय कोणीय संवेग के साथ LLL अवस्था का एकल कण तरंग है, तो मल्टीपार्टिकल वेवफंक्शन के लिए लाफलिन एनाट्ज़ है।
![{\displaystyle \langle z_{1},z_{2},z_{3},\ldots ,z_{N}\mid n,N\rangle =\psi _{n,N}(z_{1},z_{2},z_{3},\ldots ,z_{N})=D\left[\prod _{N\geqslant i>j\geqslant 1}\left(z_{i}-z_{j}\right)^{n}\right]\prod _{k=1}^{N}\exp \left(-\mid z_{k}\mid ^{2}\right)}](/index.php?title=Special:MathShowImage&hash=7ec7c0db24a9a762e82e83c1306eb0f5&mode=mathml)
जहां स्थिति द्वारा दर्शाया गया है

(गाऊसी इकाइयों) में

और  और
और  , xy समतल में निर्देशांक हैं। यहाँ
, xy समतल में निर्देशांक हैं। यहाँ  घटी हुई प्लैंक नियतांक है,
घटी हुई प्लैंक नियतांक है,  इलेक्ट्रॉन आवेश है,
इलेक्ट्रॉन आवेश है,  कणों की कुल संख्या है, और
कणों की कुल संख्या है, और  चुंबकीय क्षेत्र है, जो xy तल के लम्बवत् है। Z पर सबस्क्रिप्ट कण की पहचान करते हैं। वेव फंक्शन के लिए फ़र्मियन का वर्णन करने के लिए, n को एक विषम पूर्णांक होना चाहिए। यह कण इंटरचेंज के तहत वेव फ़ंक्शन को एंटीसिमेट्रिक होने के लिए मजबूर करता है। इस स्थिति के लिए कोणीय गति
चुंबकीय क्षेत्र है, जो xy तल के लम्बवत् है। Z पर सबस्क्रिप्ट कण की पहचान करते हैं। वेव फंक्शन के लिए फ़र्मियन का वर्णन करने के लिए, n को एक विषम पूर्णांक होना चाहिए। यह कण इंटरचेंज के तहत वेव फ़ंक्शन को एंटीसिमेट्रिक होने के लिए मजबूर करता है। इस स्थिति के लिए कोणीय गति  है।
है।
दो कणों के लिए परस्पर क्रिया की ऊर्जा

चित्र 1. सहभागिता ऊर्जा बनाम।

के लिए

और

. ऊर्जा की इकाइयों में है

. ध्यान दें कि न्यूनतम के लिए

होता है और

. सामान्य तौर पर मिनीमा

होता है
लॉफलिन वेवफंक्शन क्वासिपार्टिकल्स के लिए मल्टीपार्टिकल वेवफंक्शन है। क्वासिपार्टिकल्स की एक जोड़ी के लिए अंतःक्रियात्मक ऊर्जा का अपेक्षित मूल्य है।

जहां जांच की गई क्षमता है (चुंबकीय क्षेत्र में अंतर्निहित दो वर्तमान लूपों के बीच कूलम्ब क्षमता देखें)

जहाँ  मिला हुआ हाइपरज्यामितीय फलन है और
मिला हुआ हाइपरज्यामितीय फलन है और  पहली तरह का बेसेल फलन है। यहाँ,
पहली तरह का बेसेल फलन है। यहाँ,  दो वर्तमान लूपों के केंद्रों के बीच की दूरी है,
दो वर्तमान लूपों के केंद्रों के बीच की दूरी है,  इलेक्ट्रॉन आवेश का परिमाण है,
इलेक्ट्रॉन आवेश का परिमाण है,  लार्मर त्रिज्या का क्वांटम संस्करण है, और
लार्मर त्रिज्या का क्वांटम संस्करण है, और  चुंबकीय क्षेत्र की दिशा में इलेक्ट्रॉन गैस की मोटाई है। दो व्यक्तिगत वर्तमान लूपों का कोणीय संवेग
चुंबकीय क्षेत्र की दिशा में इलेक्ट्रॉन गैस की मोटाई है। दो व्यक्तिगत वर्तमान लूपों का कोणीय संवेग 
 है जहाँ
है जहाँ  है। व्युत्क्रम स्क्रीनिंग लंबाई (गाऊसी इकाइयों) द्वारा दी गई है
है। व्युत्क्रम स्क्रीनिंग लंबाई (गाऊसी इकाइयों) द्वारा दी गई है

जहाँ  साइक्लोट्रॉन आवृत्ति है, और
साइक्लोट्रॉन आवृत्ति है, और  xy तल में इलेक्ट्रॉन गैस का क्षेत्रफल है।
xy तल में इलेक्ट्रॉन गैस का क्षेत्रफल है।
अंतःक्रियात्मक ऊर्जा का मूल्यांकन:

|
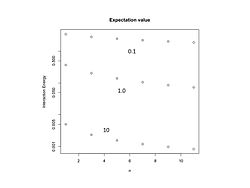
चित्र 2. सहभागिता ऊर्जा बनाम।

के लिए

और

.

ऊर्जा की इकाइयों में है
इस परिणाम को प्राप्त करने के लिए हमने एकीकरण चर में परिवर्तन किया है

और

और विख्यात (क्वांटम क्षेत्र सिद्धांत में सामान्य समाकलन देखें)
![{\displaystyle {1 \over \left(2\pi \right)^{2}\;2^{2n}\;n!}\int d^{2}z_{1}\;d^{2}z_{2}\;\mid z_{1}-z_{2}\mid ^{2n}\;\exp \left[-2\left(\mid z_{1}\mid ^{2}+\mid z_{2}\mid ^{2}\right)\right]\;{\mathcal {J}}_{0}\left({\sqrt {2}}\;{k\mid z_{1}-z_{2}\mid }\right)=}](/index.php?title=Special:MathShowImage&hash=101c272186e252afc449dc8d237dab15&mode=mathml)
![{\displaystyle {1 \over \left(2\pi \right)^{2}\;2^{n}\;n!}\int d^{2}u_{12}\;d^{2}v_{12}\;\mid u_{12}\mid ^{2n}\;\exp \left[-2\left(\mid u_{12}\mid ^{2}+\mid v_{12}\mid ^{2}\right)\right]\;{\mathcal {J}}_{0}\left({2}k\mid u_{12}\mid \right)=}](/index.php?title=Special:MathShowImage&hash=f7e2b110cda81f5023209a3bc8ec4451&mode=mathml)

अंतःक्रियात्मक ऊर्जा के लिए मिनिमा है (चित्र 1)

और

कोणीय संवेग के अनुपात के इन मानों के लिए, ऊर्जा को चित्र 2 में  के एक फलन के रूप में अंकित किया गया है।
के एक फलन के रूप में अंकित किया गया है।
संदर्भ
- ↑ Z. F. Ezewa (2008). क्वांटम हॉल प्रभाव, दूसरा संस्करण. World Scientific. ISBN 978-981-270-032-2. pp. 210-213
यह भी देखें
- लैंडौ स्तर
- फ्रैक्शनल क्वांटम हॉल इफेक्ट
- चुंबकीय क्षेत्र में एम्बेडेड दो वर्तमान लूपों के बीच कूलम्ब क्षमता

