डेलाउने शोधन
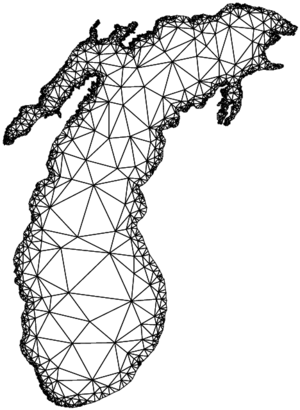
मेश जनरेशन में, डेलाउने रिफाइनमेंट मेश जनरेशन के लिए एल्गोरिदम हैं, जो मेश किए जाने वाले इनपुट की ज्योमेट्री में स्टेनर पॉइंट्स को जोड़ने के सिद्धांत पर आधारित है, जो गुणवत्ता की आवश्यकताओं को पूरा करने के लिए संवर्धित इनपुट के डेलाउने ट्रायंगुलेशन या विवश डेलाउने ट्राइएंगुलेशन का कारण बनता है। मेशिंग एप्लिकेशन का डेलाउने शोधन विधियों में च्यू द्वारा और रूपर्ट द्वारा विधियाँ सम्मिलित हैं।
च्यू का दूसरा एल्गोरिथम
च्यू का दूसरा एल्गोरिद्म एक टुकड़ावार रैखिक कई गुना प्रणाली (पीएलएस) लेता है और केवल गुणवत्ता त्रिकोणों का एक विवश डेलाउने त्रिभुज देता है जहां गुणवत्ता को त्रिकोण में न्यूनतम कोण द्वारा परिभाषित किया जाता है। तीन आयामी अंतरिक्ष में एम्बेडेड सतहों को जोड़ने के लिए एल. पॉल च्यू द्वारा विकसित,[1] च्यू के दूसरे एल्गोरिद्म को कुछ स्थितियों में रूपर्ट के एल्गोरिद्म पर व्यावहारिक लाभ के कारण द्वि-आयामी जाल जनरेटर के रूप में अपनाया गया है और यह स्वतंत्र रूप से उपलब्ध त्रिभुज (सॉफ्टवेयर) पैकेज में कार्यान्वित डिफ़ॉल्ट गुणवत्ता जाल जनरेटर है।[2] च्यू के दूसरे एल्गोरिद्म को कम से कम 28.6 डिग्री तक के न्यूनतम कोण के साथ एक स्थानीय विशेषता आकार-श्रेणी के मेश को समाप्त करने और उत्पादन करने की आश्वासन है।[3]
एल्गोरिथम इनपुट वर्टिकल के विवश डेलाउने त्रिभुज के साथ प्रारंभ होता है। प्रत्येक चरण पर, एक खराब-गुणवत्ता वाले त्रिभुज का परिकेन्द्र एक अपवाद के साथ त्रिभुज में डाला जाता है: यदि परिकेन्द्र खराब गुणवत्ता वाले त्रिभुज के रूप में इनपुट खंड के विपरीत दिशा में स्थित है, तो खंड का मध्यबिंदु सम्मिलित किया जाता है। इसके अतिरिक्त, मूल खंड (विभाजित होने से पहले) के व्यास की गेंद के अंदर पहले से डाले गए परिकेन्द्रों को त्रिकोणासन से हटा दिया जाता है।
परिधि सम्मिलन तब तक दोहराया जाता है जब तक कि कोई खराब-गुणवत्ता वाला त्रिकोण उपस्थित न हो।
रूपर्ट का एल्गोरिदम
रूपर्ट का एल्गोरिदम एक प्लानर स्ट्रेट-लाइन ग्राफ लेता है (या दो पीसवाइज लीनियर मैनिफोल्ड प्रणाली से अधिक आयाम में) और केवल गुणवत्ता वाले त्रिकोणों के अनुरूप डेलाउने ट्राइएंगुलेशन देता है। एक त्रिकोण को खराब-गुणवत्ता वाला माना जाता है, यदि उसके पास कुछ निर्धारित सीमा से कम से कम किनारे का अनुपात बड़ा हो।
1990 के दशक की शुरुआत में जिम रूपर्ट द्वारा खोजा गया,[4]
द्वि-आयामी गुणवत्ता जाल पीढ़ी के लिए रूपर्ट का एल्गोरिदम संभवतः व्यवहार में वास्तव में संतोषजनक होने वाला पहला सैद्धांतिक रूप से गारंटीकृत जाल एल्गोरिदम है।[5]
प्रेरणा
कम्प्यूटेशनल द्रव गतिकी जैसे कंप्यूटर सिमुलेशन करते समय, एक मॉडल के साथ प्रारंभ होता है जैसे कि विंग अनुभाग की 2 डी रूपरेखा 2डी परिमित तत्व विधि के लिए इनपुट को त्रिकोण के रूप में होना चाहिए जो सभी जगह को भरता है, और प्रत्येक त्रिकोण को एक प्रकार के पदार्थ से भरा जाना चाहिए - इस उदाहरण में, या तो हवा या पंख लंबे, पतले त्रिकोणों को स्पष्ट रूप से सिम्युलेट नहीं किया जा सकता है। सिमुलेशन समय सामान्यतः त्रिभुजों की संख्या के समानुपाती होता है, और इसलिए कोई त्रिभुजों की संख्या को कम करना चाहता है, जबकि अभी भी यथोचित स्पष्ट परिणाम देने के लिए पर्याप्त त्रिकोणों का उपयोग कर रहा है - सामान्यतः एक असंरचित ग्रिड का उपयोग करके। कंप्यूटर बहुभुज मॉडल को परिमित तत्व विधि के लिए उपयुक्त त्रिकोण में परिवर्तित करने के लिए रूपर्ट के एल्गोरिथ्म (या कुछ समान मेशिंग एल्गोरिदम) का उपयोग करता है।
एल्गोरिदम
एल्गोरिथम इनपुट शीर्षों के डेलाउने त्रिभुज से प्रारंभ होता है और फिर इसमें दो मुख्य ऑपरेशन होते हैं।
- गैर-रिक्त व्यासीय वृत्तों वाले खण्ड के मध्यबिंदु को त्रिकोणासन में प्रविष्ट किया जाता है।
- खराब-गुणवत्ता वाले त्रिभुज का परिकेंद्र त्रिभुज में डाला जाता है, जब तक कि यह परिकेन्द्र किसी खंड के व्यासीय वृत्त में स्थित न हो। इस स्थिति में, अतिक्रमित खंड इसके अतिरिक्त विभाजित हो जाता है।
ये ऑपरेशन तब तक दोहराए जाते हैं जब तक कि कोई खराब-गुणवत्ता वाला त्रिकोण उपस्थित न हो और सभी खंडों का अतिक्रमण न हो जाए।
स्यूडोकोड
function Ruppert(points, segments, threshold) is
T := DelaunayTriangulation(points)
Q := the set of encroached segments and poor quality triangles
while Q is not empty: // The main loop
if Q contains a segment s:
insert the midpoint of s into T
else Q contains poor quality triangle t:
if the circumcenter of t encroaches a segment s:
add s to Q;
else:
insert the circumcenter of t into T
end if
end if
update Q
end while
return T
end Ruppert.
व्यावहारिक उपयोग
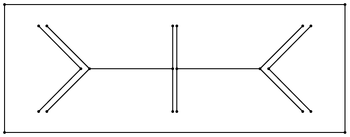
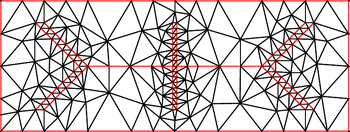
संशोधन के बिना रूपर्ट के एल्गोरिथ्म को गैर-तीव्र इनपुट और लगभग 20.7 डिग्री से कम किसी भी खराब-गुणवत्ता वाली सीमा के लिए एक गुणवत्ता जाल को समाप्त करने और उत्पन्न करने की आश्वासन है। इन प्रतिबंधों में ढील देने के लिए कई छोटे-छोटे सुधार किए गए हैं। छोटे इनपुट कोणों के पास गुणवत्ता की आवश्यकता को शिथिल करके, एल्गोरिथ्म को किसी भी सीधी रेखा के इनपुट को संभालने के लिए बढ़ाया जा सकता है।[6] समान विधियों का उपयोग करके घुमावदार इनपुट को भी मेश किया जा सकता है।[7]
रूपर्ट के एल्गोरिदम को स्वाभाविक रूप से तीन आयामों तक बढ़ाया जा सकता है, चूँकि स्लिवर प्रकार टेट्राहेड्रॉन के कारण इसकी आउटपुट आश्वासन कुछ अशक्त है।
रूपर्ट के एल्गोरिथम का दो आयामों में विस्तार मुक्त रूप से उपलब्ध त्रिभुज (सॉफ्टवेयर) पैकेज में प्रयुक्त किया गया है। इस पैकेज में रूपर्ट के एल्गोरिद्म के दो रूपों को लगभग 26.5 डिग्री की खराब-गुणवत्ता सीमा के लिए समाप्त करने की आश्वासन दी गई है।[8] व्यवहार में ये एल्गोरिदम 30 डिग्री से अधिक खराब-गुणवत्ता वाले थ्रेसहोल्ड के लिए सफल होते हैं। चूँकि, ऐसे उदाहरण ज्ञात हैं जो एल्गोरिथम को 29.06 डिग्री से अधिक सीमा के साथ विफल करने का कारण बनते हैं।[9]
यह भी देखें
- स्थानीय सुविधा का आकार
- बहुभुज जाल
- टेटजेन
- वोरोनोई आरेख
संदर्भ
- ↑ Chew, L. Paul (1993). "घुमावदार सतहों के लिए गारंटी-गुणवत्ता वाली जाली बनाना". Proceedings of the Ninth Annual Symposium on Computational Geometry. pp. 274–280.
- ↑ Shewchuk, Jonathan (2002). "त्रिकोणीय जाल पीढ़ी के लिए Delaunay शोधन एल्गोरिदम". Computational Geometry: Theory and Applications. 22 (1–3): 21–74. doi:10.1016/s0925-7721(01)00047-5.
- ↑ Rand, Alexander (2011). "च्यू का दूसरा डेलाउने शोधन एल्गोरिथम कहां और कैसे काम करता है" (PDF). Proceedings of the 23rd Canadian Conference on Computational Geometry. pp. 157–162.
- ↑ Ruppert, Jim (1995). "A Delaunay refinement algorithm for quality 2-dimensional mesh generation". Journal of Algorithms. 18 (3): 548–585. doi:10.1006/jagm.1995.1021.
- ↑ Shewchuk, Jonathan (12 August 1996). "रूपर्ट का डेलाउने शोधन एल्गोरिथम". Retrieved 28 December 2018.
- ↑ Miller, Gary; Pav, Steven; Walkington, Noel (2005). "डेलाउने शोधन एल्गोरिदम कब और क्यों काम करता है". International Journal of Computational Geometry and Applications. 15 (1): 25–54. doi:10.1142/S0218195905001592.
- ↑ Pav, Steven; Walkington, Noel (2005). Delaunay refinement by corner lopping. Proceedings of the 14th International Meshing Roundtable. pp. 165–181.
- ↑ Shewchuk, Jonathan (2002). "त्रिकोणीय जाल पीढ़ी के लिए Delaunay शोधन एल्गोरिदम". Computational Geometry: Theory and Applications. 22 (1–3): 21–74. doi:10.1016/s0925-7721(01)00047-5.
- ↑ Rand, Alexander (2011). "रूपर्ट के एल्गोरिदम के लिए गैर-समाप्ति के बेहतर उदाहरण". arXiv:1103.3903 [cs.CG]..
अग्रिम पठन
- Rineau, Laurent. "2D Conforming Triangulations and Meshes". Retrieved 28 December 2018.
- Shewchuk, Jonathan. "Triangle: A Two-Dimensional Quality Mesh Generator and Delaunay Triangulator". Retrieved 28 December 2018.
- Si, Hang (2015). "TetGen: A Quality Tetrahedral Mesh Generator and a 3D Delaunay Triangulator". Archived from the original on 29 December 2018. Retrieved 28 December 2018.
{{cite web}}: CS1 maint: bot: original URL status unknown (link)