स्नेक लेम्मा

स्नेक लेम्मा एक उपकरण है जिसका उपयोग गणित में किया जाता है, विशेष रूप से होमोलॉजिकल बीजगणित में, लंबे सटीक अनुक्रमों के निर्माण के लिए। स्नेक लेम्मा हर एबेलियन श्रेणी में मान्य है और होमोलॉजिकल बीजगणित और इसके अनुप्रयोगों में एक महत्वपूर्ण उपकरण है, उदाहरण के लिए बीजगणितीय टोपोलॉजी में। इसकी सहायता से निर्मित होमोमोर्फिज्म को आम तौर पर 'कनेक्टिंग होमोमोर्फिज्म' कहा जाता है।

कथन

एबेलियन श्रेणी में (जैसे कि एबेलियन समूहों की श्रेणी या किसी दिए गए क्षेत्र (बीजगणित) पर वेक्टर रिक्त स्थान की श्रेणी), एक कम्यूटेटिव आरेख पर विचार करें:

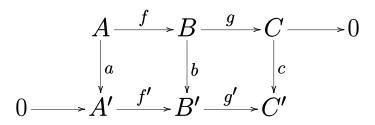जहाँ पंक्तियाँ सटीक क्रम हैं और 0 शून्य वस्तु है।

फिर ए, बी, और सी के कर्नेल (श्रेणी सिद्धांत) और cokernel से संबंधित एक सटीक अनुक्रम है:

$\ker a~{\color {Gray}\longrightarrow }~\ker b~{\color {Gray}\longrightarrow }~\ker c~{\overset {d}{\longrightarrow }}~\operatorname {coker} a~{\color {Gray}\longrightarrow }~\operatorname {coker} b~{\color {Gray}\longrightarrow }~\operatorname {coker} c$

जहाँ d एक समरूपता है, जिसे संयोजक समरूपता के रूप में जाना जाता है।

इसके अलावा, यदि आकृतिवाद f एक एकरूपता है, तो आकारिकी भी है $\ker a~{\color {Gray}\longrightarrow }~\ker b$, और यदि जी 'अधिरूपता है, तो ऐसा है $\operatorname {coker} b~{\color {Gray}\longrightarrow }~\operatorname {coker} c$.

यहाँ कोकर्नेल हैं: $\operatorname {coker} a=A'/\operatorname {im} a$, $\operatorname {coker} b=B'/\operatorname {im} b$, $\operatorname {coker} c=C'/\operatorname {im} c$.

नाम की व्याख्या

यह देखने के लिए कि स्नेक लेम्मा को इसका नाम कहां मिलता है, उपरोक्त आरेख को इस प्रकार विस्तृत करें:

और फिर सटीक क्रम जो कि लेम्मा का निष्कर्ष है, इस विस्तारित आरेख पर एक रेंगने वाले सांप के उल्टे S आकार में खींचा जा सकता है।

नक्शों का निर्माण

मानचित्र d के निर्माण का एक एनीमेशन में कुछ x दिया गया है

आरेख की क्रमविनिमेयता के कारण दिए गए (क्षैतिज) मानचित्रों द्वारा गुठली और कोकर्नेल के बीच के मानचित्रों के बीच के मानचित्रों को प्राकृतिक तरीके से प्रेरित किया जाता है। मूल आरेख की पंक्तियों की सटीकता से दो प्रेरित अनुक्रमों की सटीकता सीधे तरीके से होती है। लेम्मा का महत्वपूर्ण कथन यह है कि एक कनेक्टिंग होमोमोर्फिज्म डी मौजूद है जो सटीक अनुक्रम को पूरा करता है।

कुछ अंगूठी (गणित) पर एबेलियन समूहों या मॉड्यूल (गणित) के मामले में, नक्शा डी निम्नानुसार बनाया जा सकता है:

केर सी में एक तत्व एक्स चुनें और इसे सी के एक तत्व के रूप में देखें; चूँकि g आच्छादक है, इसलिए B में g(y) = x के साथ y मौजूद है। आरेख की क्रमविनिमेयता के कारण, हमारे पास g'(b(y)) = c(g(y)) = c(x) = 0 है (क्योंकि x, c के कर्नेल में है), और इसलिए b(y) g' के कर्नेल में है। चूंकि नीचे की पंक्ति बिल्कुल सटीक है, इसलिए हमें A' में f '(z) = b(y) के साथ एक तत्व z मिलता है। f' के इंजेक्शन द्वारा z अद्वितीय है। फिर हम d(x) = z + im(a) को परिभाषित करते हैं। अब किसी को यह जांचना है कि डी अच्छी तरह से परिभाषित है (यानी, डी (एक्स) केवल एक्स पर निर्भर करता है और वाई की पसंद पर नहीं), यह एक समरूपता है, और परिणामी लंबा अनुक्रम वास्तव में सटीक है। क्रमविनिमेय रेखाचित्र#आरेख का पीछा करते हुए नियमित रूप से सटीकता को सत्यापित किया जा सकता है (प्रमेयिका 9.1 का प्रमाण देखें) ).

एक बार ऐसा हो जाने के बाद, रिंग के ऊपर एबेलियन समूहों या मॉड्यूल के लिए प्रमेय सिद्ध हो जाता है। सामान्य मामले के लिए, तर्क को तत्वों के बजाय तीरों और रद्दीकरण के गुणों के संदर्भ में दोहराया जा सकता है। वैकल्पिक रूप से, कोई मिशेल के एम्बेडिंग प्रमेय का आह्वान कर सकता है।

स्वाभाविकता

अनुप्रयोगों में, अक्सर यह दिखाने की आवश्यकता होती है कि लंबे सटीक अनुक्रम प्राकृतिक हैं (प्राकृतिक परिवर्तनों के अर्थ में)। यह सर्प लेम्मा द्वारा निर्मित अनुक्रम की स्वाभाविकता से अनुसरण करता है।

अगर

सटीक पंक्तियों के साथ एक क्रमविनिमेय आरेख है, तो सांप लेम्मा को दो बार आगे और पीछे दो बार लागू किया जा सकता है, जिससे दो लंबे सटीक क्रम मिलते हैं; ये प्रपत्र के क्रमविनिमेय आरेख द्वारा संबंधित हैं

उदाहरण

होने देना $k$ फील्ड रहो, $V$ एक हो $k$-सदिश स्थल। $V$ है $k[t]$-मॉड्यूल द्वारा $t:V\to V$ होने के नाते $k$-रैखिक परिवर्तन, तो हम टेंसर कर सकते हैं $V$ और $k$ ऊपर $k[t]$.

$V\otimes _{k[t]}k=V\otimes _{k[t]}(k[t]/(t))=V/tV=\operatorname {coker} (t).$

का संक्षिप्त सटीक क्रम दिया गया है $k$-वेक्टर रिक्त स्थान $0\to M\to N\to P\to 0$, हम एक सटीक अनुक्रम प्रेरित कर सकते हैं $M\otimes _{k[t]}k\to N\otimes _{k[t]}k\to P\otimes _{k[t]}k\to 0$ टेंसर उत्पाद की सही सटीकता से। लेकिन क्रम $0\to M\otimes _{k[t]}k\to N\otimes _{k[t]}k\to P\otimes _{k[t]}k\to 0$ सामान्य तौर पर सटीक नहीं है। इसलिए स्वाभाविक प्रश्न उठता है। यह क्रम सटीक क्यों नहीं है?

उपरोक्त आरेख के अनुसार, हम एक सटीक अनुक्रम प्रेरित कर सकते हैं $\ker(t_{M})\to \ker(t_{N})\to \ker(t_{P})\to M\otimes _{k[t]}k\to N\otimes _{k[t]}k\to P\otimes _{k[t]}k\to 0$ स्नेक लेम्मा लगाने से। इस प्रकार, सांप लेम्मा टेन्सर उत्पाद की सटीक होने में विफलता को दर्शाता है।

समूहों की श्रेणी में

जबकि होमोलॉजिकल बीजगणित के कई परिणाम, जैसे कि पांच लेम्मा या नौ लेम्मा, एबेलियन श्रेणियों के साथ-साथ समूहों की श्रेणी में भी हैं, साँप लेम्मा नहीं है। दरअसल, मनमाना कोकर्नेल मौजूद नहीं है। हालाँकि, कोकर्नेल को (बाएं) कोसेट द्वारा प्रतिस्थापित किया जा सकता है $A'/\operatorname {im} a$, $B'/\operatorname {im} b$, और $C'/\operatorname {im} c$. फिर कनेक्टिंग होमोमोर्फिज्म को अभी भी परिभाषित किया जा सकता है, और सांप लेम्मा के बयान के रूप में अनुक्रम लिख सकते हैं। यह हमेशा एक चेन कॉम्प्लेक्स होगा, लेकिन यह सटीक होने में विफल हो सकता है। सटीकता का दावा किया जा सकता है, हालांकि, जब आरेख में लंबवत अनुक्रम सटीक होते हैं, यानी, जब ए, बी, और सी की छवियां सामान्य उपसमूह होती हैं।

प्रति उदाहरण

वैकल्पिक समूह पर विचार करें $A_{5}$: इसमें सममित समूह के लिए एक उपसमूह आइसोमोर्फिक होता है $S_{3}$, जो बदले में चक्रीय समूहों के अर्ध-प्रत्यक्ष उत्पाद के रूप में लिखा जा सकता है: $S_{3}\simeq C_{3}\rtimes C_{2}$. यह निम्नलिखित आरेख को सटीक पंक्तियों के साथ जन्म देता है:

${\begin{matrix}&1&\to &C_{3}&\to &C_{3}&\to 1\\&\downarrow &&\downarrow &&\downarrow \\1\to &1&\to &S_{3}&\to &A_{5}\end{matrix}}$

ध्यान दें कि मध्य स्तंभ सटीक नहीं है: $C_{2}$ अर्ध-प्रत्यक्ष उत्पाद में सामान्य उपसमूह नहीं है।

तब से $A_{5}$ सरल समूह है, दाएँ लंबवत तीर में तुच्छ कोकर्नेल है। इस बीच भागफल समूह $S_{3}/C_{3}$ के लिए आइसोमॉर्फिक है $C_{2}$. सर्प प्रमेयिका के कथन में क्रम इसलिए है

$1\longrightarrow 1\longrightarrow 1\longrightarrow 1\longrightarrow C_{2}\longrightarrow 1$,

जो वास्तव में सटीक होने में विफल रहता है।

लोकप्रिय संस्कृति में

1980 की फिल्म इट्स माई टर्न (फिल्म) की शुरुआत में जिल क्लेबर्ग के चरित्र द्वारा सांप लेम्मा का प्रमाण सिखाया जाता है। इट्स माई टर्न।

यह भी देखें

• ज़िगज़ैग लेम्मा

संदर्भ

• Lang, Serge (2002). "III §9 The Snake Lemma". Algebra (3rd ed.). Springer. pp. 157–9. ISBN 978-0-387-95385-4.
• Atiyah, M.F.; Macdonald, I. G. (1969). Introduction to Commutative Algebra. Addison–Wesley. ISBN 0-201-00361-9.
• Hilton, P.; Stammbach, U. (1997). A course in homological algebra. Graduate Texts in Mathematics. Springer. p. 99. ISBN 0-387-94823-6.

बाहरी संबंध

• Weisstein, Eric W. "Snake Lemma". MathWorld.
• Snake Lemma at PlanetMath
• Proof of the Snake Lemma in the film It's My Turn