भूकंपीय इंटरफेरोमेट्री

उपसतह के बारे में उपयोगी जानकारी हासिल करने के लिए इंटरफेरोमेट्री संकेतों के जोड़े के बीच सामान्य हस्तक्षेप की घटनाओं की जांच करती है। भूकंपीय इंटरफेरोमेट्री (एसआई) किसी दिए गए मीडिया के आवेग प्रतिक्रिया के पुनर्निर्माण के लिए सिग्नल जोड़े के क्रॉसकॉर्रेलाशन का उपयोग करता है। पेपर्स बाय केइटी अकी (1957), गेज़ा कुनेत्ज़ और जॉन क्लेरबाउट (1968) के पत्रों ने भूकंपीय अनुप्रयोगों के लिए तकनीक विकसित करने में मदद की और वह ढांचा प्रदान किया जिस पर आधुनिक सिद्धांत आधारित है।

एक स्थान A पर एक संकेत को एक स्थान B पर एक संकेत के साथ क्रॉसकॉरिनेट किया जा सकता है ताकि भूकंपीय इंटरफेरमेट्री का उपयोग करके एक आभासी स्रोत-रिसीवर जोड़ी को पुन: उत्पन्न किया जा सके। क्रोसोक्रेलेशन को प्रायः इस दृष्टिकोण में महत्वपूर्ण गणितीय ऑपरेशन माना जाता है, लेकिन समान परिणाम प्राप्त करने के लिए कनवल्शन का उपयोग करना भी संभव है। एक मुक्त सतह पर मापा गया निष्क्रिय ध्वनि का परस्पर संबंध उपसतह प्रतिक्रिया को पुन: उत्पन्न करता है जैसे कि यह आवेगी बिंदु स्रोत से प्रेरित था, जो परिभाषा के अनुसार, ग्रीन के कार्य के बराबर है। इस प्रकार, सक्रिय भूकंपीय स्रोत की आवश्यकता के बिना उपसतह के बारे में जानकारी प्राप्त करना संभव है। यद्यपि, यह विधि निष्क्रिय स्रोतों तक सीमित नहीं है, और इसे भूकंपीय स्रोत और कंप्यूटर-जनित तरंगो के उपयोग के लिए बढ़ाया जा सकता है।

छवि उपसतह की जांच के लिए भूकंपीय तरंगों की उपयोगिता दिखाती है

2006 तक भूकंपीय इंटरफेरोमेट्री के क्षेत्र ने भूभौतिकी के भूकंपीय ध्वनि को देखने के तरीके को बदलना शुरू कर दिया था। भूकंपीय इंटरफेरोमेट्री इस पूर्व-उपेक्षित पृष्ठभूमि वेवफील्ड का उपयोग नई जानकारी प्रदान करने के लिए करती है जिसका उपयोग उलटा समस्या के रूप में उपसतह के मॉडल के निर्माण के लिए किया जा सकता है। संभावित अनुप्रयोग महाद्वीप पैमाने से लेकर बहुत छोटे पैमाने के प्राकृतिक खतरों, औद्योगिक और पर्यावरणीय अनुप्रयोगों तक होते हैं।

इतिहास और विकास

जॉन क्लेरबाउट (1968) ने उथली उपसतह की जांच के लिए मौजूदा इंटरफेरोमेट्री तकनीकों को लागू करने के लिए एक कार्यप्रवाह विकसित किया, यद्यपि बाद में यह साबित नहीं हुआ कि भूकंपीय इंटरफेरोमेट्री को वास्तविक विश्व मीडिया पर लागू किया जा सकता है। यादृच्छिक अल्ट्रासाउंड तरंगों का दीर्घकालिक औसत एक एल्यूमीनियम ब्लॉक पर दो बिंदुओं के बीच आवेग प्रतिक्रिया का पुनर्निर्माण कर सकता है। यद्यपि, उन्होंने वास्तविक दुनिया की स्थितियों में इंटरफेरोमेट्री को सीमित करते हुए यादृच्छिक फैलाने वाले ध्वनि को मान लिया था। इसी तरह की स्थितियो में, यह दिखाया गया था कि असंबद्ध ध्वनि स्रोतों के लिए भाव दो रिसीवरों पर अवलोकनों के एकल परस्पर संबंध को कम करते हैं। प्रारंभ में केवल सतह और प्रत्यक्ष तरंग आगमन के लिए, प्रारंभ में केवल सतह और प्रत्यक्ष तरंग आगमन के लिएउपसतह की इंटरफेरोमेट्रिक आवेग प्रतिक्रिया को केवल पृष्ठभूमि ध्वनि के विस्तारित रिकॉर्ड का उपयोग करके पुनर्निर्माण किया जा सकता है।

सतह या उपसतह पर सक्रिय और निष्क्रिय दोनों स्रोतों से भूकंपीय संकेतों के परस्पर संबंध का उपयोग उपसतह के एक वैध मॉडल के पुनर्निर्माण के लिए किया जा सकता है। भूकंपीय इंटरफेरोमेट्री तरंग क्षेत्र या परिवेश स्रोतों के प्रसार पर सीमाओं के बिना संकीर्ण तरीकों के समान परिणाम उत्पन्न कर सकती है। ड्रिलिंग एप्लिकेशन में, डाउनहोल स्थान से सटे उपसतह की छवि के लिए आभासी स्रोत का उपयोग करना संभव है। विशेष रूप से सब्सल्ट सेटिंग्स में अन्वेषण के लिए इस एप्लिकेशन का तेजी से उपयोग किया जाता है।

गणितीय और भौतिक व्याख्या

भूकंपीय इंटरफेरोमेट्री दो भूकंपीय निशानों के परस्पर संबंधों का उपयोग करके उपसतह प्रतिबिंब प्रतिक्रिया के पुनर्निर्माण की संभावना प्रदान करती है। हाल ही के कार्य ने गणितीय रूप से एक हानिरहित, 3D विषम माध्यम में तरंग क्षेत्र पारस्परिकता प्रमेय का उपयोग करते हुए ग्रीन के कार्य के पुनर्निर्माण के लिए क्रॉस-रेलिसेमेंट के अनुप्रयोगों का प्रदर्शन किया है। निशान प्रायः निष्क्रिय पृष्ठभूमि ध्वनि के विस्तारित रिकॉर्ड होते हैं, लेकिन उद्देश्य के आधार पर सक्रिय स्रोतों का उपयोग करना भी संभव है। भूकंपीय इंटरफेरोमेट्री अनिवार्य रूप से उपसतह की छवि के लिए आसन्न रिसीवर स्थानों के बीच चरण अंतर का पता लगाता है।

विधि के वैध होने की शर्तें, जिसका अर्थ है कोरलेशनित संकेतों से ग्रीन के कार्य को पुनः प्राप्त करना, निम्नानुसार दी गई हैं:

• स्रोत समय में असंबद्ध हैं,
• सतह तरंग के पुनर्निर्माण के लिए स्रोत रिसीवर के चारों ओर स्थित हैं,
• वेवफ़ील्ड समविभाजित है, जिसका अर्थ है कि इसमें P तरंग और S तरंग दोनों सम्मिलित हैं।

अंतिम दो शर्तों को सीधे प्रकृति में पूरा करना कठिन है। यद्यपि, तरंग प्रकीर्णन के कारण, तरंगें परिवर्तित हो जाती हैं, जो समविभाजन की स्थिति को संतुष्ट करती है। स्रोतों का समान वितरण इस तथ्य के कारण मिलता है कि तरंगें हर दिशा में बिखरी हुई हैं।

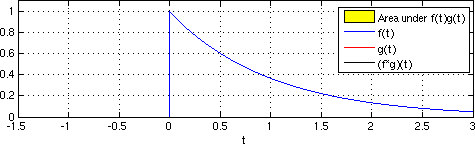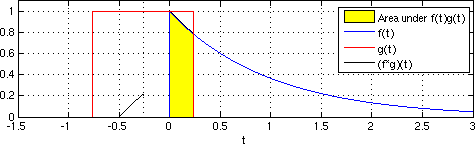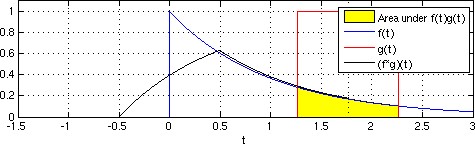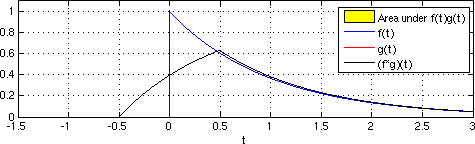
भूकंपीय इंटरफेरोमेट्री में सरल क्रॉसकॉर्रेलाशन और वास्तविक रिसीवर प्रतिक्रियाओं का ढेर होता है ताकि आवेग प्रतिक्रिया का अनुमान लगाया जा सके जैसे कि लागू रिसीवर के स्थान पर आभासी स्रोत रखा गया था। समय डोमेन में निरंतर कार्यों का परस्पर संबंध समीकरण 1 के रूप में प्रस्तुत किया गया है।

समीकरण 1

$(f_{1}*f_{2})(t)=\int f_{1}(\lambda )f_{2}(\lambda -t)d\lambda$

जहां कार्यों को विभिन्न अंतराल मूल्यों पर समय के कार्य के रूप में एकीकृत किया जाता है। को अवधारणात्मक रूप से समझा जा सकता है क्योंकि दो अलग-अलग रिसीवर स्थानों में तरंगों से जुड़े ट्रैवलटाइम लैग के रूप में है। क्रॉसकोरलेशन कनवल्शन के समान है जहां दूसरा फ़ंक्शन पहले के सापेक्ष मुड़ा हुआ है।

भूकंपीय इंटरफेरोमेट्री मूल रूप से ऑप्टिकल इंटरफेरोमेट्री के समान है जो एक ग्लास लेंस से गुजरने वाली प्रत्यक्ष और परावर्तित तरंग के हस्तक्षेप से उत्पन्न होती है जहां तीव्रता मुख्य रूप से चरण घटक पर निर्भर होती है।

कनवल्शन का सिद्धांत। क्रोसोक्रेलेशन के समान

समीकरण 2

I = 1+2R2 cos[ω(λAr+λrB)]+R^4

जहां: तीव्रता प्रतिबिंब गुणांक (R) और चरण घटक ω(λAr+λrB) के परिमाण से संबंधित है। परावर्तकता वितरण का अनुमान एक स्थान A पर प्रत्यक्ष तरंग के परस्पर संबंध के माध्यम से एक स्थान B पर दर्ज प्रतिबिंब के साथ प्राप्त किया जा सकता है जहां A संदर्भ ट्रेस का प्रतिनिधित्व करता है। A पर ट्रेस स्पेक्ट्रम के संयुग्मन और B पर ट्रेस स्पेक्ट्रम का गुणन देता है:

समीकरण 3

ФAB =Re^iω(λAr+λrB) + o.t.

जहां: ФAB = उत्पाद स्पेक्ट्रम o.t. = अतिरिक्त शर्तें, और प्रत्यक्ष-प्रत्यक्ष का कोरलेशन, आदि। पिछली स्थितियो की तरह, उत्पाद स्पेक्ट्रम चरण का एक कार्य है।

कुंजी: परावर्तक ज्यामिति में परिवर्तन से कोरलेशन परिणाम में परिवर्तन होता है और प्रवासन कर्नेल के अनुप्रयोग के माध्यम से परावर्तक ज्यामिति को पुनर्प्राप्त किया जा सकता है। कच्चे इंटरफेरोग्राम की व्याख्या का सामान्य रूप से प्रयास नहीं किया जाता है; क्रॉसकोरलेशन परिणाम सामान्यतः किसी प्रकार के माइग्रेशन का उपयोग करके संसाधित किए जाते हैं।

सबसे सरल स्थित में, सतह पर जियोफोन द्वारा दर्ज की गई गहराई विकिरण ऊर्जा पर घूर्णन ड्रिल की बिट पर विचार करें। यह मान लेना संभव है कि किसी दिए गए स्थान पर स्रोत वेवलेट का चरण यादृच्छिक है और स्रोत स्थान के बारे में किसी भी ज्ञान के बिना एक स्थान बी पर एक आवांछित प्रतिबिम्ब के साथ एक स्थान बी पर प्रत्यक्ष तरंग के क्रॉसकोरलेशन का उपयोग करता है। आवृति डोमेन में निशान A और B का परस्पर संबंध इस प्रकार सरल होता है:

समीकरण 4

Ф(A, B) = −(Wiω)^2 Re^iω(λArλrB)+o.t.

जहां: वाई (ω) = आवृत्ति डोमेन स्रोत तरंगिका (इथ तरंगिका)

किसी स्थान A पर प्रत्यक्ष तरंग का परस्पर संबंध किसी स्थान B पर आवांछित प्रतिबिम्ब के साथ अज्ञात स्रोत शब्द को हटा देता है जहां:

समीकरण 5

Ф(A,B)≈Re^iω(λArλrB)

यह प्रपत्र एक स्थान पर आभासी स्रोत विन्यास के बराबर है एक स्थान बी पर एक इमेजिंग काल्पनिक प्रतिबिंब, इन कोरलेशन पदों का प्रवास चरण अवधि को हटा देता है और स्थिति x पर एक अंतिम प्रवासन छवि उत्पन्न करता है जहां:

m(x) = Σø(A,B,λAx+λxB)

जहां: ø(A,B,t) = अंतराल समय टी के साथ स्थानों ए और बी के बीच अस्थायी संबंध

इस मॉडल को पश्चिम टेक्सास में उपसतह ज्यामिति का अनुकरण करने के लिए एक संकीर्ण अंतर्हित स्रोत और समान परिणाम उत्पन्न करने के लिए एक सिंथेटिक (आभासी) घूर्णन ड्रिल बिट स्रोत सहित सिम्युलेटेड मॉडल का उपयोग करने के लिए लागू किया गया है। इसी तरह के एक मॉडल ने नकली उपसतह ज्यामिति के पुनर्निर्माण का प्रदर्शन किया। इस स्थित में, पुनर्निर्मित उपसतह प्रतिक्रिया ने प्राथमिक और गुणकों की सापेक्ष स्थिति को सही ढंग से प्रतिरूपित किया। विभिन्न प्रकार की स्थितियो में सिग्नल ज्यामिति के पुनर्निर्माण के लिए अतिरिक्त समीकरण प्राप्त किए जा सकते हैं।

अनुप्रयोग

भूकंपीय इंटरफेरोमेट्री वर्तमान में मुख्य रूप से अनुसंधान और शैक्षणिक सेटिंग्स में उपयोग की जाती है। एक उदाहरण में, दक्षिणी कैलिफोर्निया में उथले उपसतह वेग विश्लेषण के लिए आवेग प्रतिक्रिया का अनुमान लगाने के लिए निष्क्रिय श्रवण और लंबे ध्वनि के निशानों के परस्पर संबंध का उपयोग किया गया था। भूकंपीय इंटरफेरोमेट्री ने विस्तृत उलटा तकनीकों का उपयोग करके संकेतित परिणाम की तुलना में एक परिणाम प्रदान किया। भूकंपीय इंटरफेरोमेट्री का उपयोग प्रायः निकट सतह की परीक्षा के लिए किया जाता है और प्रायः केवल सतह और प्रत्यक्ष तरंगों के पुनर्निर्माण के लिए उपयोग किया जाता है। जैसे, भूकंपीय इंटरफेरोमेट्री का उपयोग सामान्यतः ग्राउंड रोल का अनुमान लगाने के लिए किया जाता है ताकि इसे हटाने में सहायता मिल सके। भूकंपीय इंटरफेरोमेट्री एक खड़ी इमारत में अपरूपण तरंग वेग और क्षीणन के अनुमानों को सरल बनाती है। भूकंपीय इंटरफेरोमेट्री को ज्वालामुखी के भूकंपीय फैलाव और वेग संरचना की छवि पर लगाया गया है।

भूकंपीय प्रदर्शन जैसा कि जियोफोन द्वारा रिकॉर्ड किया गया है

अन्वेषण और उत्पादन

तेजी से, भूकंपीय इंटरफेरोमेट्री को हाइड्रोकार्बन अन्वेषण और उत्पादन में जगह मिल रही है। एसआई नमक के गुंबदों से सटे अवसादों की छवि बना सकता है। संकीर्ण भूकंपीय परावर्तन तकनीकों का उपयोग करके जटिल नमक ज्यामिति को खराब तरीके से हल किया जाता है। एक वैकल्पिक विधि डाउनहोल स्रोतों और उपसतह नमक सुविधाओं के निकट रिसीवर के उपयोग के लिए कॉल करती है। डाउनहोल स्थान में आदर्श भूकंपीय संकेत उत्पन्न करना प्रायः मुश्किल होता है। भूकंपीय इंटरफेरोमेट्री वास्तव में एक स्रोत को एक डाउनहोल स्थान में स्थानांतरित कर सकता है, ताकि एक नमक गुंबद के बगल में अच्छी तरह से रोशन किया जा सके और तीव्र गति से डायपिंग तलछट को कैप्चर किया जा सके। इस स्थित में, एसआई परिणाम वास्तविक डाउनहोल स्रोत का उपयोग करके प्राप्त किए गए परिणाम के समान था। भूकंपीय इंटरफेरोमेट्री एक अज्ञात स्रोत की स्थिति का पता लगा सकती है और इसका उपयोग प्रायः हाइड्रो-फ्रेशिंग अनुप्रयोगों में प्रेरित फ्रैक्चर की सीमा को मैप करने के लिए किया जाता है। यह संभव है कि उपसतह में जलाशय गुणों में सूक्ष्म परिवर्तनों की टाइमलैप्स भूकंपीय निगरानी के लिए इंटरफेरोमेट्रिक तकनीकों को लागू किया जा सकता है।

सीमाएं

भूकंपीय इंटरफेरोमेट्री अनुप्रयोग वर्तमान में कई कारकों द्वारा सीमित हैं। वास्तविक विश्व मीडिया और ध्वनि वर्तमान सैद्धांतिक विकास की सीमाओं का प्रतिनिधित्व करते हैं। उदाहरण के लिए, इंटरफेरोमेट्री के काम करने के लिए निष्क्रिय भूकंपीय को असंबद्ध होना चाहिए और पूरी तरह से रुचि के क्षेत्र को घेरना चाहिए। इसके अलावा, क्षीणन और ज्यामितीय प्रसार को काफी हद तक उपेक्षित किया गया है और इसे और अधिक मजबूत मॉडल में सम्मिलित करने की आवश्यकता है। अन्य चुनौतियाँ भूकंपीय इंटरफेरोमेट्री में निहित हैं। उदाहरण के लिए, स्रोत शब्द केवल एक स्थान ए पर एक प्रत्यक्ष लहर के क्रॉस कोरलेशन के स्थित में एक स्थान बी पर एक आवांछित प्रतिबिम्ब के साथ समाप्त हो जाता है। अन्य तरंगों का कोरलेशन परिणामी इंटरफेरोग्राम के गुणकों को पेश कर सकता है। वेग विश्लेषण और फ़िल्टरिंग किसी दिए गए डेटासेट में गुणकों की घटना को कम कर सकते हैं लेकिन समाप्त नहीं कर सकते हैं।

यद्यपि भूकंपीय इंटरफेरोमेट्री में कई प्रगति हुई हैं, फिर भी चुनौतियाँ बनी हुई हैं। सबसे बड़ी शेष चुनौतियों में से एक सिद्धांत को वास्तविक विश्व मीडिया और उपसतह में ध्वनि वितरण के लिए विस्तार करना है। प्राकृतिक स्रोत सामान्यतः गणितीय सामान्यीकरण का पालन नहीं करते हैं और वास्तव में कुछ हद तक कोरलेशन प्रदर्शित कर सकते हैं। भूकंपीय इंटरफेरोमेट्री के अनुप्रयोगों के अधिक व्यापक होने से पहले अतिरिक्त समस्याओं का समाधान किया जाना चाहिए।

संदर्भ

• Bakulin, A.; Calvert, R. (2004). "Virtual source: new method for imaging and 4D below complex overburden". SEG Expanded Abstracts: 2477–2480. doi:10.1190/1.1845233.
• Brenguer, F.; Shapiro, N. (2007). "3D surface wave tomography of the Piton de la Fournaise volcano using seismic noise correlations". Geophysical Research Letters. 34 (2): L02305. Bibcode:2007GeoRL..34.2305B. doi:10.1029/2006gl028586.
• Campillo, H.; Paul, A. (2003). "Longrange correlations in the diffuse seismic coda". Science. 299 (5606): 547–549. Bibcode:2003Sci...299..547C. doi:10.1126/science.1078551. PMID 12543969. S2CID 22021516.
• Chaput, J.; Zandomeneghi, D.; Aster, R.; Knox, H.A.; Kyle, P.R. (2012). "Imaging of Erebus volcano using body wave seismic interferometry of Strombolian eruption coda". Geophysical Research Letters. 39 (7): n/a. Bibcode:2012GeoRL..39.7304C. doi:10.1029/2012gl050956.
• Curtis, A.; Gerstoft, P.; Sato, H.; Snieder, R.; Wapenaar, K. (2006). "Seismic interferometry turning noise into signal". The Leading Edge. 25 (9): 1082–1092. doi:10.1190/1.2349814.
• Draganov, D.; Wapenaar, K.; Thorbecke, J. (2006). "Seismic interferometry: Reconstructing the earth's reflection response". Geophysics. 71 (4): SI61–SI70. Bibcode:2006Geop...71SI.61D. CiteSeerX 10.1.1.75.113. doi:10.1190/1.2209947.
• Hornby, B.; Yu, J. (2007). "Interferometric imaging of a salt flank using walkaway VSP data". The Leading Edge. 26 (6): 760–763. doi:10.1190/1.2748493.
• Lu, R.; Willis, M.; Campman, X.; Franklin, J.; Toksoz, M. (2006). "Imaging dipping sediments at a salt dome flankVSP seismic interferometry and reversetime migration". SEG Expanded Abstracts: 2191–2195. doi:10.1190/1.2369970.
• Schuster, G.; Yu, J.; Sheng, J.; Rickett, J. (2004). "Interferometric/daylight seismic imaging". Geophysical Journal International. 157 (2): 838–852. Bibcode:2004GeoJI.157..838S. doi:10.1111/j.1365-246x.2004.02251.x.
• Yu, J.; Followill, F.; Schuster, G. (2003). "Autocorrelogram migration of IVSPWD data: Field data test". Geophysics. 68 (1): 297–307. Bibcode:2003Geop...68..297Y. doi:10.1190/1.1543215.
• Weaver, R.; Lobkis, O. (2001). "Ultrasonics without a source: Thermal fluctuation correlations at MHz frequencies". Physical Review Letters. 87 (13): 134301. Bibcode:2001PhRvL..87m4301W. doi:10.1103/PhysRevLett.87.134301. PMID 11580591.