आइसोगोनल संयुग्म

__नोटोक__

  Angle bisectors (concur at incenter I)

  Lines from each vertex to P

  Lines to P reflected about the angle bisectors (concur at P*, the isogonal conjugate of P)

त्रिभुज के अंदर बिंदुओं पर आइसोगोनल संयुग्म परिवर्तन।

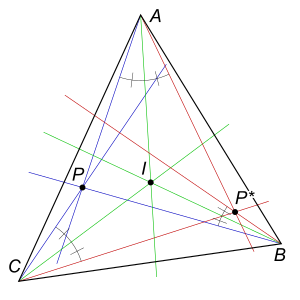
ज्यामिति में, एक बिंदु (ज्यामिति) के आइसोगोनल संयुग्म P त्रिभुज के संबंध में △ABC का निर्माण रेखाओं के परावर्तन (गणित) द्वारा किया जाता है PA, PB, PC के कोण द्विभाजक के बारे में A, B, C क्रमश। ये तीन परावर्तित रेखाएँ समकोणिक संयुग्म पर समवर्ती रेखाएँ हैं P. (यह परिभाषा केवल उन बिंदुओं पर लागू होती है जो त्रिभुज की विस्तारित भुजा पर नहीं हैं △ABC.) यह सेवा के प्रमेय के त्रिकोणमितीय रूप का प्रत्यक्ष परिणाम है।

एक बिंदु का आइसोगोनल संयुग्म P को कभी-कभी निरूपित किया जाता है P*. का आइसोगोनल संयुग्म P* है P.

अंतःकेंद्र का आइसोगोनल संयुग्म I ही है। लम्बकेन्द्र का आइसोगोनल संयुग्म H परिकेन्द्र है O. केन्द्रक का आइसोगोनल संयुग्म G (परिभाषा के अनुसार) सिम्मेडियन बिंदु है K. फर्मेट बिंदु के आइसोगोनल कॉन्जुगेट्स आइसोडायनामिक बिंदु ्स हैं और इसके विपरीत। ब्रोकार्ड बिंदु एक दूसरे के समकोणीय संयुग्म हैं।

ट्रिलिनियर निर्देशांक में, यदि $X=x:y:z$ त्रिभुज की भुजा पर नहीं एक बिंदु है △ABC, तो इसका समद्विबाहु संयुग्म है ${\tfrac {1}{x}}:{\tfrac {1}{y}}:{\tfrac {1}{z}}.$ इस कारण से, का आइसोगोनल संयुग्म X को कभी-कभी निरूपित किया जाता है X ^–1. सेट (गणित) {{mvar|S}त्रिरेखीय गुणनफल के अंतर्गत त्रिभुज केंद्रों का }, द्वारा परिभाषित

$(p:q:r)*(u:v:w)=pu:qv:rw,$

क्रमविनिमेय समूह है, और प्रत्येक का व्युत्क्रम है X में S है X ^–1.

जैसा कि आइसोगोनल संयुग्मन एक फ़ंक्शन (गणित) है, यह बिंदुओं के सेट, जैसे कि रेखाओं और वृत्तों के आइसोगोनल संयुग्मन के बारे में बात करने के लिए समझ में आता है। उदाहरण के लिए, एक रेखा का आइसोगोनल संयुग्म एक खतना और प्रतिष्ठित है; विशेष रूप से, एक दीर्घवृत्त, परवलय या अतिपरवलय के अनुसार रेखा परिवृत्त को 0, 1, या 2 बिंदुओं में काटती है। परिवृत्त का समकोणीय संयुग्म अनंत पर रेखा है। कई प्रसिद्ध क्यूबिक समतल वक्र (जैसे, थॉमसन क्यूबिक, डार्बौक्स क्यूबिक, न्युबर्ग क्यूबिक ) स्व-समकोणीय-संयुग्मी हैं, इस अर्थ में कि यदि X क्यूबिक पर है, तो X ^–1 क्यूबिक पर भी है।

== एक बिंदु == के आइसोगोनल संयुग्म के लिए एक और निर्माण

आइसोगोनल संयुग्म की दूसरी परिभाषा

किसी दिए गए बिंदु के लिए P त्रिभुज के तल में △ABC, के प्रतिबिंब चलो P पार्श्व में BC, CA, AB होना P_a, P_b, P_c. फिर वृत्त का केंद्र 〇P_aP_bP_c का आइसोगोनल संयुग्म है P.

यह भी देखें

• समस्थानिक संयुग्म
• सेंट्रल लाइन (ज्यामिति)
• त्रिकोण केंद्र

बाहरी संबंध

• Interactive Java Applet illustrating isogonal conjugate and its properties
• MathWorld
• Pedal Triangle and Isogonal Conjugacy