विसंधित-सेट डेटा संरचना

Disjoint-set/Union-find Forest
Type	multiway tree
Invented	1964
Invented by	Bernard A. Galler and Michael J. Fischer
Time complexity in big O notation
Algorithm Average Worst case Space O(n) O(n) Search O(α(n)) O(α(n)) Merge O(α(n)) O(α(n))

MakeSet 8 सिंगलटन बनाता है।

के कुछ ऑपरेशन के बाद Union, कुछ सेट एक साथ समूहीकृत किए जाते हैं।

कंप्यूटर विज्ञान में, एक असम्बद्ध-सबसेट डेटा संरचना, जिसे संघ-खोज डेटा संरचना या मर्ज-खोज सेट भी कहा जाता है, एक डेटा संरचना है जो अलग-अलग सेट (गैर-ओवरलैपिंग) सेट (गणित) का संग्रह संग्रहीत करती है। समतुल्य रूप से, यह एक सेट के एक विभाजन को असंबद्ध उपसमुच्चय में संग्रहीत करता है। यह नए सेट जोड़ने, मर्ज करने वाले सेट (उन्हें उनके संघ (सेट सिद्धांत) द्वारा प्रतिस्थापित करने) और एक सेट के प्रतिनिधि सदस्य को खोजने के लिए संचालन प्रदान करता है। अंतिम संक्रिया कुशलतापूर्वक यह पता लगाना संभव बनाती है कि क्या कोई दो तत्व एक ही या अलग-अलग सेट में हैं।

जबकि असंयुक्त-सेट डेटा संरचनाओं को लागू करने के कई तरीके हैं, व्यवहार में उन्हें अक्सर एक विशेष कार्यान्वयन के साथ पहचाना जाता है जिसे असम्बद्ध-सेट वन कहा जाता है। यह एक विशेष प्रकार का वन (ग्राफ सिद्धांत) है जो संघों को निष्पादित करता है और निकट-निरंतर परिशोधित विश्लेषण में पाता है। का क्रम करने के लिए m जोड़, संघ, या असम्बद्ध-सेट फ़ॉरेस्ट पर संचालन खोजें n नोड्स को कुल समय की आवश्यकता होती है O(mα(n)), कहाँ α(n) बेहद धीमी गति से बढ़ने व्युत्क्रम एकरमैन समारोह है। विसंधित वन प्रति-कार्रवाई के आधार पर इस प्रदर्शन की गारंटी नहीं देते हैं। व्यक्तिगत संघ और खोज संचालन एक स्थिर समय से अधिक समय ले सकते हैं α(n) समय, लेकिन प्रत्येक ऑपरेशन डिसजॉइंट-सेट फ़ॉरेस्ट को स्वयं को समायोजित करने का कारण बनता है ताकि क्रमिक संचालन तेज़ हो। असम्बद्ध-सेट फ़ॉरेस्ट असम्बद्ध रूप से इष्टतम और व्यावहारिक रूप से कुशल दोनों हैं।

ग्राफ़ के न्यूनतम फैले पेड़ को खोजने के लिए क्रुस्कल के एल्गोरिदम में अलग-अलग सेट डेटा संरचनाएं महत्वपूर्ण भूमिका निभाती हैं। न्यूनतम फैले हुए पेड़ों के महत्व का अर्थ है कि अलग-अलग सेट डेटा संरचनाएं विभिन्न प्रकार के एल्गोरिदम के अंतर्गत आती हैं। इसके अलावा, अलग-अलग सेट डेटा संरचनाओं में प्रतीकात्मक संगणना के साथ-साथ संकलक में भी अनुप्रयोग होते हैं, विशेष रूप से रजिस्टर आवंटन समस्याओं के लिए।

इतिहास

1964 में बर्नार्ड ए. गैलर और माइकल जे. फिशर द्वारा डिसजॉइंट-सेट वनों का पहली बार वर्णन किया गया था। 1973 में, उनकी समय जटिलता को सीमित कर दिया गया था $O(\log ^{*}(n))$, का पुनरावृत्त लघुगणक $n$, जॉन हॉपक्रॉफ्ट और जेफरी उल्मैन द्वारा। 1975 में, रॉबर्ट टार्जन साबित करने वाले पहले व्यक्ति थे $O(m\alpha (n))$ (एकरमैन फ़ंक्शन # उलटा) एल्गोरिथम की समय जटिलता पर ऊपरी सीमा, और, 1979 में, दिखाया कि यह एक प्रतिबंधित मामले के लिए निचली सीमा थी। 1989 में, माइकल फ्रेडमैन और माइकल सक्स (गणितज्ञ) ने इसे दिखाया $\Omega (\alpha (n))$ (परिशोधित) शब्दों को किसी भी असम्बद्ध-सेट डेटा संरचना प्रति ऑपरेशन द्वारा एक्सेस किया जाना चाहिए, जिससे डेटा संरचना की इष्टतमता साबित होती है।

1991 में, गैलील और इटालियनो ने अलग-अलग सेटों के लिए डेटा संरचनाओं का एक सर्वेक्षण प्रकाशित किया। 1994 में, रिचर्ड जे. एंडरसन और हीथर वोल ने यूनियन-फाइंड के समानांतर संस्करण का वर्णन किया जिसे कभी ब्लॉक करने की आवश्यकता नहीं है। 2007 में, सिल्वेन कॉनचॉन और जीन-क्रिस्टोफ़ फ़िलिआट्रे ने असंयुक्त-सेट फ़ॉरेस्ट डेटा संरचना का एक अर्ध-स्थायी डेटा संरचना संस्करण विकसित किया और सबूत सहायक Coq का उपयोग करके इसकी शुद्धता को औपचारिक रूप दिया। सेमी-पर्सिस्टेंट का अर्थ है कि संरचना के पिछले संस्करणों को कुशलता से बनाए रखा जाता है, लेकिन डेटा संरचना के पिछले संस्करणों तक पहुंच बाद के संस्करणों को अमान्य कर देती है। उनका सबसे तेज़ कार्यान्वयन गैर-स्थायी एल्गोरिदम के रूप में लगभग उतना ही कुशल प्रदर्शन प्राप्त करता है। वे एक जटिलता विश्लेषण नहीं करते हैं।

समस्याओं के प्रतिबंधित वर्ग पर बेहतर प्रदर्शन के साथ अलग-अलग सेट डेटा संरचनाओं के रूपों पर भी विचार किया गया है। गैबो और टारजन ने दिखाया कि यदि संभावित संघों को कुछ खास तरीकों से प्रतिबंधित किया जाता है, तो वास्तव में रैखिक समय एल्गोरिथम संभव है।

प्रतिनिधित्व

असंयुक्त-सेट फ़ॉरेस्ट में प्रत्येक नोड में एक सूचक और कुछ सहायक जानकारी होती है, या तो आकार या रैंक (लेकिन दोनों नहीं)। पॉइंटर्स का उपयोग पैरेंट पॉइंटर ट्री बनाने के लिए किया जाता है, जहाँ प्रत्येक नोड जो ट्री की जड़ नहीं है, अपने पैरेंट को इंगित करता है। रूट नोड्स को दूसरों से अलग करने के लिए, उनके पैरेंट पॉइंटर्स में अमान्य मान होते हैं, जैसे कि नोड या प्रहरी मान के लिए एक परिपत्र संदर्भ। प्रत्येक पेड़ जंगल में संग्रहीत एक सेट का प्रतिनिधित्व करता है, जिसमें सेट के सदस्य पेड़ में नोड होते हैं। रूट नोड सेट प्रतिनिधि प्रदान करते हैं: दो नोड एक ही सेट में होते हैं यदि और केवल यदि नोड्स वाले पेड़ों की जड़ें बराबर होती हैं।

फ़ॉरेस्ट में नोड्स को किसी भी तरह से एप्लिकेशन के लिए सुविधाजनक रूप से संग्रहीत किया जा सकता है, लेकिन एक सामान्य तकनीक उन्हें एक सरणी में संग्रहीत करना है। इस मामले में, माता-पिता को उनके सरणी सूचकांक द्वारा इंगित किया जा सकता है। प्रत्येक सरणी प्रविष्टि की आवश्यकता होती है Θ(log n) पेरेंट पॉइंटर के लिए स्टोरेज के बिट्स। शेष प्रविष्टि के लिए एक तुलनात्मक या कम मात्रा में संग्रहण की आवश्यकता होती है, इसलिए फ़ॉरेस्ट को संग्रहीत करने के लिए आवश्यक बिट्स की संख्या है Θ(n log n). यदि कोई कार्यान्वयन निश्चित आकार के नोड्स का उपयोग करता है (जिससे जंगल के अधिकतम आकार को सीमित किया जा सकता है), तो आवश्यक भंडारण रैखिक है n.

संचालन

डिसजॉइंट-सेट डेटा स्ट्रक्चर्स तीन ऑपरेशनों का समर्थन करते हैं: एक नया सेट बनाना जिसमें एक नया तत्व होता है; किसी दिए गए तत्व वाले सेट के प्रतिनिधि को ढूँढना; और दो सेटों को मर्ज करना।

=== नए सेट बनाना === MakeSet ई> ऑपरेशन एक नए तत्व को एक नए सेट में जोड़ता है जिसमें केवल नया तत्व होता है, और नया सेट डेटा संरचना में जोड़ा जाता है। यदि डेटा संरचना को सेट के विभाजन के रूप में देखा जाता है, तो MakeSet ऑपरेशन नए तत्व को जोड़कर सेट को बढ़ाता है, और यह नए तत्व को केवल नए तत्व वाले नए उपसमुच्चय में डालकर मौजूदा विभाजन का विस्तार करता है।

असंबद्ध वन में, MakeSet नोड के पैरेंट पॉइंटर और नोड के आकार या रैंक को इनिशियलाइज़ करता है। यदि एक जड़ को एक नोड द्वारा दर्शाया जाता है जो स्वयं को इंगित करता है, तो निम्नलिखित स्यूडोकोड का उपयोग करके एक तत्व जोड़ना वर्णित किया जा सकता है:

समारोह MakeSet(x) है
    अगर x पहले से ही जंगल में नहीं है तो
        x.parent := x
        x.size := 1 // if node store size
        x.रैंक := 0 // अगर नोड्स स्टोर रैंक
    अगर अंत
अंत समारोह

इस ऑपरेशन में निरंतर समय जटिलता है। विशेष रूप से, प्रारंभ a असंबद्ध सेट वन के साथ n नोड्स की आवश्यकता है O(n) समय।

व्यवहार में, MakeSet एक ऑपरेशन से पहले होना चाहिए जो मेमोरी को होल्ड करने के लिए आवंटित करता है x. जब तक स्मृति आवंटन एक परिशोधित निरंतर-समय का संचालन है, क्योंकि यह एक अच्छे गतिशील सरणी कार्यान्वयन के लिए है, यह यादृच्छिक-सेट फ़ॉरेस्ट के स्पर्शोन्मुख प्रदर्शन को नहीं बदलता है।

=== सेट प्रतिनिधि ढूँढना === Find ई> ऑपरेशन एक निर्दिष्ट क्वेरी नोड से पैरेंट पॉइंटर्स की श्रृंखला का अनुसरण करता है x जब तक यह मूल तत्व तक नहीं पहुंच जाता। यह मूल तत्व उस सेट का प्रतिनिधित्व करता है जिससे x का है और हो सकता है x अपने आप। Find यह जिस मूल तत्व तक पहुंचता है उसे वापस कर देता है।

प्रदर्शन कर रहा है Find ऑपरेशन जंगल में सुधार के लिए एक महत्वपूर्ण अवसर प्रस्तुत करता है। ए में समय Find ऑपरेशन पैरेंट पॉइंटर्स का पीछा करते हुए खर्च किया जाता है, इसलिए एक चापलूसी वाला पेड़ तेजी से आगे बढ़ता है Find संचालन। जब एक Find निष्पादित किया जाता है, उत्तराधिकार में प्रत्येक पैरेंट पॉइंटर का अनुसरण करने की तुलना में रूट तक पहुंचने का कोई तेज़ तरीका नहीं है। हालाँकि, इस खोज के दौरान देखे गए पैरेंट पॉइंटर्स को रूट के करीब इंगित करने के लिए अपडेट किया जा सकता है। चूँकि रूट के रास्ते में देखा गया प्रत्येक तत्व उसी सेट का हिस्सा होता है, इससे फ़ॉरेस्ट में संग्रहीत सेट नहीं बदलते हैं। लेकिन यह भविष्य बनाता है Find संचालन तेजी से, न केवल क्वेरी नोड और रूट के बीच के नोड्स के लिए, बल्कि उनके वंशजों के लिए भी। यह अद्यतन असंबद्ध-सेट फ़ॉरेस्ट की परिशोधित प्रदर्शन गारंटी का एक महत्वपूर्ण हिस्सा है।

के लिए कई एल्गोरिदम हैं Find जो विषम रूप से इष्टतम समय जटिलता प्राप्त करते हैं। एल्गोरिदम का एक परिवार, जिसे पथ संपीड़न के रूप में जाना जाता है, प्रत्येक नोड को क्वेरी नोड और रूट बिंदु से रूट के बीच बनाता है। पथ संपीड़न को एक साधारण पुनरावर्तन का उपयोग करके निम्नानुसार कार्यान्वित किया जा सकता है:

फ़ंक्शन Find(x) है
    अगर x.parent ≠ x तो
        x.parent := Find(x.parent)
        रिटर्न x.parent
    अन्य
        रिटर्न एक्स
    अगर अंत
अंत समारोह

यह कार्यान्वयन दो मार्ग बनाता है, एक पेड़ के ऊपर और एक पीछे की ओर। क्वेरी नोड से रूट तक पथ को संग्रहीत करने के लिए पर्याप्त स्क्रैच मेमोरी की आवश्यकता होती है (उपरोक्त स्यूडोकोड में, कॉल स्टैक का उपयोग करके पथ को स्पष्ट रूप से दर्शाया गया है)। इसे एक ही दिशा में दोनों पास करके स्मृति की निरंतर मात्रा में घटाया जा सकता है। निरंतर मेमोरी कार्यान्वयन क्वेरी नोड से रूट तक दो बार चलता है, एक बार रूट को खोजने के लिए और एक बार पॉइंटर्स को अपडेट करने के लिए:

फ़ंक्शन Find(x) है
    जड़ := x
    जबकि रूट.पैरेंट ≠ रूट करते हैं
        रूट := रूट.पैरेंट
    जबकि समाप्त करें

    जबकि x.parent ≠ root करते हैं
        अभिभावक := x.जनक
        x.parent := जड़
        एक्स := पैरेंट
    जबकि समाप्त करें

    रिटर्न रूट
अंत समारोह

रॉबर्ट ई. टारजन और जॉन वैन लीउवेन ने भी वन-पास विकसित किया Find एल्गोरिदम जो सबसे खराब स्थिति वाली जटिलता को बनाए रखते हैं लेकिन व्यवहार में अधिक कुशल होते हैं। इन्हें पाथ स्प्लिटिंग और पाथ हॉलिंग कहा जाता है। ये दोनों क्वेरी नोड और रूट के बीच के पथ पर नोड्स के पैरेंट पॉइंटर्स को अपडेट करते हैं। पथ विभाजन प्रत्येक पैरेंट पॉइंटर को उस पथ पर एक पॉइंटर द्वारा नोड के दादा-दादी के लिए बदल देता है:

फ़ंक्शन Find(x) है
    जबकि x.parent ≠ x करते हैं
        (x, x.parent) := (x.parent, x.parent.parent)
    जबकि समाप्त करें
    रिटर्न एक्स
अंत समारोह

पाथ हॉल्टिंग समान रूप से काम करता है लेकिन केवल हर दूसरे पैरेंट पॉइंटर को बदलता है:

फ़ंक्शन Find(x) है
    जबकि x.parent ≠ x करते हैं
        x.parent := x.parent.parent
        x := x.parent
    जबकि समाप्त करें
    रिटर्न एक्स
अंत समारोह

दो सेटों का विलय

संचालन Union(x, y) युक्त सेट को प्रतिस्थापित करता है x और सेट युक्त y उनके संघ के साथ। Union पहला उपयोग करता है Find युक्त पेड़ों की जड़ों का निर्धारण करने के लिए x और y. यदि जड़ें समान हैं, तो कुछ और करने को नहीं है। अन्यथा, दो पेड़ों को मिला देना चाहिए। यह या तो पैरेंट पॉइंटर सेट करके किया जाता है x की जड़ y's, या के पैरेंट पॉइंटर को सेट करना y की जड़ x'एस।

कौन सा नोड माता-पिता बनने का विकल्प पेड़ पर भविष्य के संचालन की जटिलता के परिणाम हैं। अगर इसे लापरवाही से किया जाए तो पेड़ अत्यधिक ऊंचे हो सकते हैं। उदाहरण के लिए, मान लीजिए Union हमेशा पेड़ युक्त बनाया x युक्त पेड़ का एक सबट्री y. एक ऐसे जंगल से शुरू करें जिसे अभी-अभी तत्वों के साथ आरंभ किया गया है $1,2,3,\ldots ,n,$ और निष्पादित करें Union(1, 2), Union(2, 3), ..., Union(n - 1, n). परिणामी जंगल में एक ही पेड़ होता है जिसकी जड़ होती है n, और 1 से पथ n ट्री में हर नोड से होकर गुजरता है। इस जंगल के लिए, चलाने का समय Find(1) है O(n).

एक कुशल कार्यान्वयन में, पेड़ की ऊंचाई को आकार या संघ द्वारा रैंक द्वारा संघ का उपयोग करके नियंत्रित किया जाता है। इन दोनों को अपने पैरेंट पॉइंटर के अलावा सूचनाओं को स्टोर करने के लिए नोड की आवश्यकता होती है। इस जानकारी का उपयोग यह तय करने के लिए किया जाता है कि कौन सा रूट नया पैरेंट बनता है। दोनों रणनीतियाँ सुनिश्चित करती हैं कि पेड़ बहुत गहरे न हों।

आकार से संघ

आकार के संघ के मामले में, एक नोड अपने आकार को संग्रहीत करता है, जो केवल इसके वंशजों की संख्या है (नोड सहित)। जब पेड़ जड़ों के साथ x और y मर्ज किए जाते हैं, तो अधिक डिसेंडेंट वाला नोड पैरेंट बन जाता है। यदि दो नोड्स के वंशजों की संख्या समान है, तो कोई भी माता-पिता बन सकता है। दोनों ही मामलों में, नए पैरेंट नोड का आकार उसके वंशजों की नई कुल संख्या पर सेट होता है।

समारोह Union(x, y) है
     // नोड्स को जड़ों से बदलें 
    x := Find(x)
    वाई := फाइंड(वाई)

    अगर x = y तब
        वापसी  // x और y पहले से ही एक ही सेट में हैं 
    अगर अंत

    // यदि आवश्यक हो, तो यह सुनिश्चित करने के लिए चर स्वैप करें 
    // x के कम से कम उतने वंशज हैं जितने y
    अगर x.size <y.size तो
        (x, y) := (y, x)
    अगर अंत

     // एक्स को नया रूट बनाएं 
    य. जनक := x
     // x का आकार अपडेट करें 
    एक्स.साइज := एक्स.साइज + वाई.साइज
अंत समारोह

आकार को स्टोर करने के लिए आवश्यक बिट्स की संख्या स्पष्ट रूप से स्टोर करने के लिए आवश्यक बिट्स की संख्या है n. यह वन के आवश्यक भंडारण में एक स्थिर कारक जोड़ता है।

रैंक द्वारा संघ

रैंक द्वारा संघ के लिए, एक नोड इसे संग्रहीत करता है rank, जो इसकी ऊंचाई के लिए एक ऊपरी सीमा है। जब एक नोड को इनिशियलाइज़ किया जाता है, तो उसकी रैंक शून्य पर सेट हो जाती है। पेड़ों को जड़ों से मिलाने के लिए x और y, पहले उनके रैंकों की तुलना करें। यदि रैंक अलग हैं, तो बड़ा रैंक ट्री माता-पिता बन जाता है, और रैंक x और y बदलें नहीं। यदि रैंक समान हैं, तो कोई भी माता-पिता बन सकता है, लेकिन नए माता-पिता की रैंक में एक की वृद्धि होती है। जबकि एक नोड का रैंक स्पष्ट रूप से इसकी ऊंचाई से संबंधित होता है, रैंकों को संग्रहित करना ऊंचाइयों को संग्रहित करने से अधिक कुशल होता है। एक नोड की ऊंचाई एक के दौरान बदल सकती है Find ऑपरेशन, इसलिए रैंकों को संग्रहित करने से ऊंचाई को सही रखने के अतिरिक्त प्रयास से बचा जाता है। स्यूडोकोड में, रैंक द्वारा संघ है:

समारोह Union(x, y) है
     // नोड्स को जड़ों से बदलें 
    x := Find(x)
    वाई := फाइंड(वाई)

    अगर x = y तब
        वापसी  // x और y पहले से ही एक ही सेट में हैं 
    अगर अंत

    // यदि आवश्यक हो, तो यह सुनिश्चित करने के लिए चर का नाम बदलें 
    // x का रैंक कम से कम y जितना बड़ा है
    अगर x.रैंक <y.रैंक तब
        (x, y) := (y, x)
    अगर अंत

     // एक्स को नया रूट बनाएं 
    य. जनक := x
    // यदि आवश्यक हो, x के रैंक में वृद्धि 
    अगर x.रैंक = y.रैंक तब
        x.रैंक := x.रैंक + 1
    अगर अंत
अंत समारोह

यह दिखाया जा सकता है कि प्रत्येक नोड में रैंक है $\lfloor \log n\rfloor$ या कम। नतीजतन प्रत्येक रैंक में संग्रहीत किया जा सकता है O(log log n) बिट्स और सभी रैंकों को स्टोर किया जा सकता है O(n log log n) बिट्स। यह रैंकों को जंगल के आकार का एक विषम रूप से नगण्य हिस्सा बनाता है।

उपरोक्त कार्यान्वयन से यह स्पष्ट है कि नोड का आकार और रैंक तब तक मायने नहीं रखता जब तक कि नोड पेड़ की जड़ न हो। एक बार जब एक नोड एक बच्चा बन जाता है, तो इसका आकार और रैंक फिर कभी नहीं देखा जाता है।

समय जटिलता

एक असम्बद्ध-सेट वन कार्यान्वयन जिसमें Find पैरेंट पॉइंटर्स को अपडेट नहीं करता है, और जिसमें Union पेड़ की ऊंचाई को नियंत्रित करने का प्रयास नहीं करता, ऊंचाई वाले पेड़ हो सकते हैं O(n). ऐसी स्थिति में द Find और Union संचालन की आवश्यकता है O(n) समय।

यदि कोई कार्यान्वयन अकेले पथ संपीड़न का उपयोग करता है, तो एक क्रम n MakeSet संचालन, उसके बाद तक n − 1 Union संचालन और f Find संचालन, का सबसे खराब समय चल रहा है $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$. रैंक द्वारा संघ का उपयोग करना, लेकिन माता-पिता पॉइंटर्स को अपडेट किए बिना Find, का चलने का समय देता है $\Theta (m\log n)$ के लिए m किसी भी प्रकार का संचालन, तक n जिनमें से हैं MakeSet संचालन।

आकार या रैंक द्वारा संघ के साथ पथ संपीड़न, विभाजन, या आधा करने का संयोजन, चलने के समय को कम करता है m किसी भी प्रकार का संचालन, तक n जिनमें से हैं MakeSet संचालन, करने के लिए $\Theta (m\alpha (n))$. यह प्रत्येक ऑपरेशन का परिशोधन विश्लेषण करता है $\Theta (\alpha (n))$. यह असम्बद्ध रूप से इष्टतम है, जिसका अर्थ है कि प्रत्येक असम्बद्ध सेट डेटा संरचना का उपयोग करना चाहिए $\Omega (\alpha (n))$ प्रति ऑपरेशन परिशोधित समय। यहाँ, समारोह $\alpha (n)$ एकरमैन फ़ंक्शन # उलटा है। व्युत्क्रम एकरमैन फ़ंक्शन असाधारण रूप से धीरे-धीरे बढ़ता है, इसलिए यह कारक है 4 या किसी के लिए कम n जो वास्तव में भौतिक ब्रह्मांड में लिखा जा सकता है। यह असंबद्ध-सेट संचालन को व्यावहारिक रूप से परिशोधित स्थिर समय बनाता है।

=== यूनियन-फाइंड === की O(m log* n) समय जटिलता का प्रमाण

एक असम्बद्ध-सेट वन के प्रदर्शन का सटीक विश्लेषण कुछ जटिल है। हालांकि, एक बहुत सरल विश्लेषण है जो यह साबित करता है कि किसी के लिए परिशोधित समय m Find या Union एक असम्बद्ध-सेट वन युक्त पर संचालन n वस्तुएं हैं O(mlog^* n), कहाँ log^* पुनरावृत्त लघुगणक को दर्शाता है।

प्रमेयिका 1: जैसे-जैसे डिसजॉइंट-सेट डेटा स्ट्रक्चर#डिसजॉइंट-सेट फ़ॉरेस्ट रूट के साथ-साथ पथ का अनुसरण करता है, नोड का रैंक बढ़ता जा रहा है।

Proof

claim that as Find and Union operations are applied to the data set, this fact remains true over time. Initially when each node is the root of its own tree, it's trivially true. The only case when the rank of a node might be changed is when the Union by Rank operation is applied. In this case, a tree with smaller rank will be attached to a tree with greater rank, rather than vice versa. And during the find operation, all nodes visited along the path will be attached to the root, which has larger rank than its children, so this operation won't change this fact either.

{{anchor|min subtree size lemma}लेम्मा 2: एक नोड u जो रैंक के साथ सबट्री का रूट है r कम से कम है $2^{r}$ नोड्स।

Proof

Initially when each node is the root of its own tree, it's trivially true. Assume that a node u with rank r has at least 2^r nodes. Then when two trees with rank r are merged using the operation Union by Rank, a tree with rank r + 1 results, the root of which has at least $2^{r}+2^{r}=2^{r+1}$ nodes.

File:ProofOflogstarnRank.jpg

लेम्मा 3: रैंक के नोड्स की अधिकतम संख्या r ज्यादा से ज्यादा है ${\frac {n}{2^{r}}}.$

Proof

From lemma 2, we know that a node u which is root of a subtree with rank r has at least $2^{r}$ nodes. We will get the maximum number of nodes of rank r when each node with rank r is the root of a tree that has exactly $2^{r}$ nodes. In this case, the number of nodes of rank r is ${\frac {n}{2^{r}}}.$

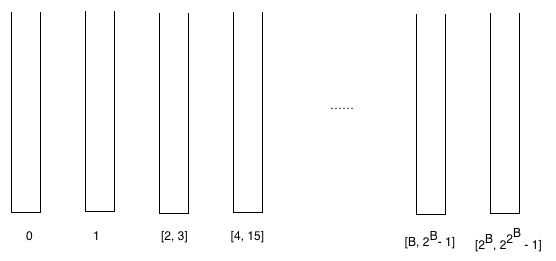
सुविधा के लिए, हम यहां बकेट को परिभाषित करते हैं: एक बकेट एक सेट है जिसमें विशेष रैंक वाले वर्टिकल होते हैं।

हम कुछ बकेट बनाते हैं और उनके रैंक के अनुसार बाल्टियों में वर्टिकल डालते हैं। यानी, रैंक 0 वाले कोने शून्य बकेट में जाते हैं, रैंक 1 वाले वर्टिकल पहली बकेट में जाते हैं, रैंक 2 और 3 वाले वर्टिकल दूसरी बकेट में जाते हैं। अगर B-थ बकेट में अंतराल से रैंक वाले वर्टिकल होते हैं $\left[r,2^{r}-1\right]=[r,R-1]$ तब (B+1)st बकेट में अंतराल से रैंक वाले शीर्ष होंगे $\left[R,2^{R}-1\right].$

का सबूत $O(\log ^{*}n)$ संघ खोजें

हम बाल्टियों के बारे में दो अवलोकन कर सकते हैं।

1. बकेट की कुल संख्या अधिक से अधिक है log^*n

   प्रमाण: जब हम एक बाल्टी से दूसरी बाल्टी में जाते हैं, तो हम शक्ति में एक और दो जोड़ देते हैं, यानी अगली बाल्टी $\left[B,2^{B}-1\right]$ होगा $\left[2^{B},2^{2^{B}}-1\right]$

2. बाल्टी में तत्वों की अधिकतम संख्या $\left[B,2^{B}-1\right]$ अधिक से अधिक है ${\frac {2n}{2^{B}}}$

   सबूत: बाल्टी में तत्वों की अधिकतम संख्या $\left[B,2^{B}-1\right]$ अधिक से अधिक है ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$

होने देना F प्रदर्शन किए गए कार्यों की सूची का प्रतिनिधित्व करते हैं, और जाने दें

$$T_{1}=\sum _{F}{\text{(link to the root)}}$$

$$T_{2}=\sum _{F}{\text{(number of links traversed where the buckets are different)}}$$

$$T_{3}=\sum _{F}{\text{(number of links traversed where the buckets are the same).}}$$

फिर की कुल लागत m पाता है $T=T_{1}+T_{2}+T_{3}.$ चूंकि प्रत्येक खोज ऑपरेशन ठीक एक ट्रैवर्सल बनाता है जो रूट की ओर जाता है, हमारे पास है T₁ = O(m).

इसके अलावा, ऊपर की सीमा से बाल्टियों की संख्या पर, हमारे पास है T₂ = O(mlog^*n).

के लिए T₃, मान लीजिए कि हम एक किनारे से गुजर रहे हैं u को v, कहाँ u और v बकेट में रैंक है [B, 2^B − 1] और v रूट नहीं है (इस ट्रैवर्सिंग के समय, अन्यथा ट्रैवर्सल का हिसाब होगा T₁). हल करना u और अनुक्रम पर विचार करें $v_{1},v_{2},\ldots ,v_{k}$ कि भूमिका निभाएं v विभिन्न खोज कार्यों में। पथ संपीड़न के कारण और किनारे को रूट के लिए लेखांकन नहीं करने के कारण, इस अनुक्रम में केवल अलग-अलग नोड होते हैं और #बढ़ती रैंक लेम्मा के कारण हम जानते हैं कि इस क्रम में नोड्स की रैंक सख्ती से बढ़ रही है। बकेट में दोनों नोड्स होने से हम यह निष्कर्ष निकाल सकते हैं कि लंबाई k अनुक्रम का (कई बार नोड u एक ही बाल्टी में एक अलग जड़ से जुड़ा हुआ है) बाल्टियों में रैंकों की अधिकतम संख्या है B, यानी ज्यादा से ज्यादा $2^{B}-1-B<2^{B}.$ इसलिए, $T_{3}\leq \sum _{[B,2^{B}-1]}\sum _{u}2^{B}.$ टिप्पणियों से #अधिकतम बाल्टियाँ और #अधिकतम बकेट आकार, हम यह निष्कर्ष निकाल सकते हैं ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ इसलिए, $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$

अनुप्रयोग

न्यूनतम फैले पेड़ को खोजने के लिए क्रुस्कल के एल्गोरिदम का उपयोग करते समय संघ-खोज के लिए एक डेमो।

असंयुक्त-सेट डेटा संरचनाएं एक सेट के विभाजन को मॉडल करती हैं, उदाहरण के लिए एक अप्रत्यक्ष ग्राफ के कनेक्टेड घटक (ग्राफ सिद्धांत) का ट्रैक रखने के लिए। इस मॉडल का उपयोग तब यह निर्धारित करने के लिए किया जा सकता है कि क्या दो कोने एक ही घटक से संबंधित हैं, या क्या उनके बीच एक किनारा जोड़ने से एक चक्र बन जाएगा। यूनियन-फाइंड एल्गोरिथम का उपयोग एकीकरण (कंप्यूटर विज्ञान) के उच्च-प्रदर्शन कार्यान्वयन में किया जाता है।

इस डेटा संरचना का उपयोग बूस्ट ग्राफ लाइब्रेरी द्वारा इसकी इंक्रीमेंटल कनेक्टेड कंपोनेंट्स कार्यक्षमता को लागू करने के लिए किया जाता है। ग्राफ़ के न्यूनतम फैले पेड़ को खोजने के लिए क्रस्कल के एल्गोरिदम को लागू करने में यह एक महत्वपूर्ण घटक भी है।

ध्यान दें कि असंयुक्त-सेट वनों के रूप में नियमित कार्यान्वयन किनारों को हटाने की अनुमति नहीं देता है, यहां तक ​​कि पथ संपीड़न या रैंक हेयुरिस्टिक के बिना भी। हालाँकि, आधुनिक कार्यान्वयन मौजूद हैं जो निरंतर-समय के विलोपन की अनुमति देते हैं।Template:Vague citation

शारीर और अग्रवाल ने डिसजॉइंट-सेट के सबसे खराब स्थिति वाले व्यवहार और डेवनपोर्ट-शिनज़ेल अनुक्रम की लंबाई के बीच संबंध की रिपोर्ट की। डेवनपोर्ट-शिनज़ेल अनुक्रम, कम्प्यूटेशनल ज्यामिति से एक संयोजन संरचना। द होशेन-कोपेलमैन_एल्गोरिदम | होशेन-कोपेलमैन एल्गोरिथम एल्गोरिथम में यूनियन-फाइंड का उपयोग करता है।

यह भी देखें

• Partition refinement, असंयुक्त सेट को बनाए रखने के लिए एक भिन्न डेटा संरचना, ऐसे अपडेट के साथ जो सेट को एक साथ मिलाने के बजाय अलग कर देता है
• Dynamic connectivity

बाहरी संबंध

• C++ implementation, part of the Boost C++ libraries
• Java implementation, part of JGraphT library
• Javascript implementation
• Python implementation
• Visual explanation and C# code