डीएफटी मैट्रिक्स

लागू गणित में, एक डीएफटी मैट्रिक्स एक परिवर्तन मैट्रिक्स के रूप में असतत फूरियर रूपांतरण (डीएफटी) की अभिव्यक्ति है, जिसे मैट्रिक्स गुणन के माध्यम से सिग्नल पर लागू किया जा सकता है।

परिभाषा

एन-पॉइंट डीएफटी को गुणन के रूप में व्यक्त किया जाता है $X=Wx$ , कहाँ $x$ मूल इनपुट संकेत है, $W$ एन-बाय-एन स्क्वायर मैट्रिक्स डीएफटी मैट्रिक्स है, और $X$ सिग्नल का डीएफटी है।

परिवर्तन मैट्रिक्स $W$ के रूप में परिभाषित किया जा सकता है $W=\left({\frac {\omega ^{jk}}{\sqrt {N}}}\right)_{j,k=0,\ldots ,N-1}$ , या समकक्ष:

W={\frac {1}{\sqrt {N}}}{\begin{bmatrix}1&1&1&1&\cdots &1\\1&\omega &\omega ^{2}&\omega ^{3}&\cdots &\omega ^{N-1}\\1&\omega ^{2}&\omega ^{4}&\omega ^{6}&\cdots &\omega ^{2(N-1)}\\1&\omega ^{3}&\omega ^{6}&\omega ^{9}&\cdots &\omega ^{3(N-1)}\\\vdots &\vdots &\vdots &\vdots &\ddots &\vdots \\1&\omega ^{N-1}&\omega ^{2(N-1)}&\omega ^{3(N-1)}&\cdots &\omega ^{(N-1)(N-1)}\end{bmatrix}}

,

कहाँ $\omega =e^{-2\pi i/N}$ एकता की जड़ है जिसमें $i^{2}=-1$ . हम के लिए बड़े घातांक लिखने से बच सकते हैं $\omega$ इस तथ्य का उपयोग करके कि किसी भी एक्सपोनेंट के लिए $x$ हमारी पहचान है $\omega ^{x}=\omega ^{x{\bmod {N}}}.$ यह सामान्यीकरण कारक तक, एकता की जड़ों के लिए वैंडरमोंड मैट्रिक्स है। ध्यान दें कि योग के सामने सामान्यीकरण कारक ( $1/{\sqrt {N}}$ ) और ω में घातांक का चिह्न केवल प्रथाएं हैं, और कुछ उपचारों में भिन्न हैं। नीचे दी गई सभी चर्चा परिपाटी पर ध्यान दिए बिना, कम से कम मामूली समायोजन के साथ लागू होती हैं। एकमात्र महत्वपूर्ण बात यह है कि आगे और व्युत्क्रम परिवर्तनों में विपरीत-चिन्ह वाले घातांक होते हैं, और यह कि उनके सामान्यीकरण कारकों का गुणनफल 1/N होता है। हालांकि $1/{\sqrt {N}}$ यहां पसंद परिणामी डीएफटी मैट्रिक्स एकात्मक मैट्रिक्स बनाता है, जो कई परिस्थितियों में सुविधाजनक है।

फास्ट फूरियर रूपांतरण एल्गोरिदम मैट्रिक्स की समरूपता का उपयोग इस मैट्रिक्स द्वारा एक वेक्टर को गुणा करने के समय को सामान्य से कम करने के लिए करता है $O(N^{2})$ . हैडमार्ड मैट्रिक्स और वॉल्श मैट्रिक्स जैसे मैट्रिसेस द्वारा गुणन के लिए इसी तरह की तकनीकों को लागू किया जा सकता है।

उदाहरण

दो-बिंदु

दो-बिंदु डीएफटी एक साधारण मामला है, जिसमें पहली प्रविष्टि डीसी पूर्वाग्रह (योग) है और दूसरी प्रविष्टि एसी गुणांक (अंतर) है।

W={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}

पहली पंक्ति योग करती है, और दूसरी पंक्ति अंतर करती है।

का कारक $1/{\sqrt {2}}$ रूपांतरण को एकात्मक बनाना है (नीचे देखें)।

चार सूत्री

चार-बिंदु दक्षिणावर्त DFT मैट्रिक्स इस प्रकार है:

W={\frac {1}{\sqrt {4}}}{\begin{bmatrix}\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}\\\omega ^{0}&\omega ^{1}&\omega ^{2}&\omega ^{3}\\\omega ^{0}&\omega ^{2}&\omega ^{4}&\omega ^{6}\\\omega ^{0}&\omega ^{3}&\omega ^{6}&\omega ^{9}\\\end{bmatrix}}={\frac {1}{\sqrt {4}}}{\begin{bmatrix}1&1&1&1\\1&-i&-1&i\\1&-1&1&-1\\1&i&-1&-i\end{bmatrix}}

कहाँ $\omega =e^{-{\frac {2\pi i}{4}}}=-i$ .

आठ-बिंदु

दो मामलों की पहली गैर-तुच्छ पूर्णांक शक्ति आठ बिंदुओं के लिए है:

W = \frac{1}{\sqrt{8}} [\begin{matrix} ω^{0} & ω^{0} & ω^{0} & ω^{0} & ω^{0} & ω^{0} & ω^{0} & ω^{0} \\ ω^{0} & ω^{1} & ω^{2} & ω^{3} & ω^{4} & ω^{5} & ω^{6} & ω^{7} \\ ω^{0} & ω^{2} & ω^{4} & ω^{6} & ω^{8} & ω^{10} & ω^{12} & ω^{14} \\ ω^{0} & ω^{3} & ω^{6} & ω^{9} & ω^{12} & ω^{15} & ω^{18} & ω^{21} \\ ω^{0} & ω^{4} & ω^{8} & ω^{12} & ω^{16} & ω^{20} & ω^{24} & ω^{28} \\ ω^{0} & ω^{5} & ω^{10} & ω^{15} & ω^{20} & ω^{25} & ω^{30} & ω^{35} \\ ω^{0} & ω^{6} & ω^{12} & ω^{18} & ω^{24} & ω^{30} & ω^{36} & ω^{42} \\ ω^{0} & ω^{7} & ω^{14} & ω^{21} & ω^{28} & ω^{35} & ω^{42} & ω^{49} \end{matrix}] = \frac{1}{\sqrt{8}} [\begin{matrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & ω & - i & - i ω & - 1 & - ω & i \end{matrix}

कहाँ

\omega =e^{-{\frac {2\pi i}{8}}}={\frac {1}{\sqrt {2}}}-{\frac {i}{\sqrt {2}}}

(ध्यान दें कि $\omega ^{8+n}=\omega ^{n}$ .)

निम्नलिखित छवि डीएफटी को मैट्रिक्स गुणन के रूप में दर्शाती है, जटिल घातांक के नमूनों द्वारा दर्शाए गए मैट्रिक्स के तत्वों के साथ:

वास्तविक भाग (कोज्या तरंग) को एक ठोस रेखा और काल्पनिक भाग (साइन तरंग) को धराशायी रेखा द्वारा दर्शाया जाता है।

शीर्ष पंक्ति सभी वाले हैं (द्वारा स्केल किया गया $1/{\sqrt {8}}$ यूनिटारिटी के लिए), इसलिए यह इनपुट सिग्नल में डीसी पूर्वाग्रह को मापता है। अगली पंक्ति एक जटिल घातांक के ऋणात्मक एक चक्र के आठ नमूने हैं, अर्थात, −1/8 की भिन्नात्मक आवृत्ति वाला एक संकेत, इसलिए यह मापता है कि संकेत में भिन्नात्मक आवृत्ति +1/8 पर कितनी शक्ति है। याद रखें कि एक मेल खाने वाला फ़िल्टर सिग्नल की तुलना हम जो कुछ भी खोज रहे हैं उसके एक समय उलट संस्करण के साथ करते हैं, इसलिए जब हम fracfreq की तलाश कर रहे हैं। 1/8 हम fracfreq से तुलना करते हैं। −1/8 इसलिए यह पंक्ति ऋणात्मक बारंबारता है। अगली पंक्ति एक जटिल घातांक के नकारात्मक दो चक्र हैं, जिन्हें आठ स्थानों पर नमूना लिया गया है, इसलिए इसमें -1/4 की भिन्नात्मक आवृत्ति है, और इस प्रकार उस सीमा को मापता है जिस तक सिग्नल की आंशिक आवृत्ति +1/4 है।

निम्नलिखित सारांशित करता है कि 8-बिंदु डीएफटी कैसे काम करता है, पंक्ति दर पंक्ति, भिन्नात्मक आवृत्ति के संदर्भ में:

0 मापता है कि सिग्नल में कितना DC है
−1/8 मापता है कि कितने सिग्नल की आंशिक आवृत्ति +1/8 है
−1/4 मापता है कि कितने सिग्नल की आंशिक आवृत्ति +1/4 है
−3/8 मापता है कि कितने सिग्नल की भिन्नात्मक आवृत्ति +3/8 है
−1/2 मापता है कि कितने सिग्नल की आंशिक आवृत्ति +1/2 है
−5/8 मापता है कि कितने सिग्नल की भिन्नात्मक आवृत्ति +5/8 है
−3/4 मापता है कि कितने सिग्नल की आंशिक आवृत्ति +3/4 है
−7/8 मापता है कि कितने सिग्नल की भिन्नात्मक आवृत्ति +7/8 है

समतुल्य रूप से अंतिम पंक्ति को +1/8 की भिन्नात्मक आवृत्ति कहा जा सकता है और इस प्रकार यह मापता है कि कितने सिग्नल की भिन्नात्मक आवृत्ति -1/8 है। इस तरह, यह कहा जा सकता है कि मैट्रिक्स की शीर्ष पंक्तियाँ संकेत में सकारात्मक आवृत्ति सामग्री को मापती हैं और नीचे की पंक्तियाँ संकेत में नकारात्मक आवृत्ति घटक को मापती हैं।

एकात्मक परिवर्तन

डीएफटी (या स्केलिंग के उचित चयन के माध्यम से हो सकता है) एक एकात्मक परिवर्तन है, यानी, जो ऊर्जा को संरक्षित करता है। एकात्मकता प्राप्त करने के लिए स्केलिंग का उपयुक्त विकल्प है $1/{\sqrt {N}}$ , ताकि भौतिक डोमेन में ऊर्जा फूरियर डोमेन में ऊर्जा के समान हो, यानी पारसेवल के प्रमेय को संतुष्ट करने के लिए। (अन्य, गैर-एकात्मक, स्केलिंग, आमतौर पर कम्प्यूटेशनल सुविधा के लिए भी उपयोग किए जाते हैं; उदाहरण के लिए, असतत फूरियर रूपांतरण लेख में दिखाए गए स्केलिंग के साथ कनवल्शन प्रमेय थोड़ा सरल रूप लेता है।)

अन्य गुण

डीएफटी मैट्रिक्स के अन्य गुणों के लिए, इसके eigenvalues सहित, कनवल्शन से कनेक्शन, एप्लिकेशन, और इसी तरह, असतत फूरियर ट्रांसफॉर्म लेख देखें।

एक सीमित मामला: फूरियर ऑपरेटर

Real part (cosine)

Imaginary part (sine)

The Fourier operator

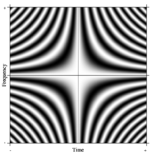
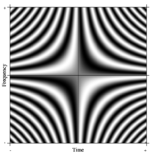
फूरियर रूपांतरण की धारणा आसानी से सामान्यीकृत फूरियर श्रृंखला है। एन-पॉइंट डीएफटी के ऐसे एक औपचारिक सामान्यीकरण की कल्पना एन को मनमाने ढंग से बड़ा करके की जा सकती है। सीमा में, कठोर गणितीय मशीनरी ऐसे रैखिक ऑपरेटरों को तथाकथित अभिन्न परिवर्तन के रूप में मानती है। इस मामले में, यदि हम पंक्तियों में जटिल घातांकों के साथ एक बहुत बड़ा मैट्रिक्स बनाते हैं (अर्थात, कोज्या वास्तविक भाग और साइन काल्पनिक भाग), और बिना सीमा के रिज़ॉल्यूशन बढ़ाते हैं, तो हम दूसरी तरह के फ्रेडहोम इंटीग्रल समीकरण के कर्नेल तक पहुँचते हैं, अर्थात् फूरियर ऑपरेटर जो निरंतर फूरियर रूपांतरण को परिभाषित करता है। इस सतत फूरियर ऑपरेटर के एक आयताकार हिस्से को एक छवि के रूप में प्रदर्शित किया जा सकता है, जो डीएफटी मैट्रिक्स के समान है, जैसा कि दाईं ओर दिखाया गया है, जहां ग्रेस्केल पिक्सेल मान संख्यात्मक मात्रा को दर्शाता है।

यह भी देखें

बहुआयामी परिवर्तन
पाउली मैट्रिसेस का सामान्यीकरण # निर्माण: घड़ी और शिफ्ट मैट्रिसेस

संदर्भ

The Transform and Data Compression Handbook by P. C. Yip, K. Ramamohan Rao – See chapter 2 for a treatment of the DFT based largely on the DFT matrix

बाहरी संबंध

Fourier Operator and Decimation In Time (DIT)

v t e Matrix classes
Explicitly constrained entries	Alternant Anti-diagonal Anti-Hermitian Anti-symmetric Arrowhead Band Bidiagonal Bisymmetric Block-diagonal Block Block tridiagonal Boolean Cauchy Centrosymmetric Conference Complex Hadamard Copositive Diagonally dominant Diagonal Discrete Fourier Transform Elementary Equivalent Frobenius Generalized permutation Hadamard Hankel Hermitian Hessenberg Hollow Integer Logical Matrix unit Metzler Moore Nonnegative Pentadiagonal Permutation Persymmetric Polynomial Quaternionic Signature Skew-Hermitian Skew-symmetric Skyline Sparse Sylvester Symmetric Toeplitz Triangular Tridiagonal Vandermonde Walsh Z
Constant	Exchange Hilbert Identity Lehmer Of ones Pascal Pauli Redheffer Shift Zero
Conditions on eigenvalues or eigenvectors	Companion Convergent Defective Definite Diagonalizable Hurwitz Positive-definite Stieltjes
Satisfying conditions on products or inverses	Congruent Idempotent or Projection Invertible Involutory Nilpotent Normal Orthogonal Unimodular Unipotent Unitary Totally unimodular Weighing
With specific applications	Adjugate Alternating sign Augmented Bézout Carleman Cartan Circulant Cofactor Commutation Confusion Coxeter Distance Duplication and elimination Euclidean distance Fundamental (linear differential equation) Generator Gram Hessian Householder Jacobian Moment Payoff Pick Random Rotation Seifert Shear Similarity Symplectic Totally positive Transformation
Used in statistics	Centering Correlation Covariance Design Doubly stochastic Fisher information Hat Precision Stochastic Transition
Used in graph theory	Adjacency Biadjacency Degree Edmonds Incidence Laplacian Seidel adjacency Tutte
Used in science and engineering	Cabibbo–Kobayashi–Maskawa Density Fundamental (computer vision) Fuzzy associative Gamma Gell-Mann Hamiltonian Irregular Overlap S State transition Substitution Z (chemistry)
Related terms	Jordan normal form Linear independence Matrix exponential Matrix representation of conic sections Perfect matrix Pseudoinverse Row echelon form Wronskian
' List of matrices Category:Matrices

Anonymous

Search

डीएफटी मैट्रिक्स

Namespaces

More

Page actions

Contents

परिभाषा