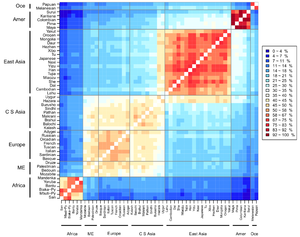
आनुवंशिक दूरी

कैवेली-स्फोर्ज़ा एट अल द्वारा आनुवंशिक दूरी का नक्शा। (1994)

आनुवंशिक दूरी प्रजातियों के बीच या एक प्रजाति के भीतर आबादी#आनुवांशिकी के बीच आनुवंशिकी विचलन का एक उपाय है, चाहे दूरी सामान्य पूर्वज या भेदभाव की डिग्री से समय को मापती है। कई समान युग्मविकल्पी वाली आबादी में छोटी आनुवंशिक दूरी होती है। यह इंगित करता है कि वे निकट से संबंधित हैं और हाल ही में एक सामान्य पूर्वज हैं।

आबादी के इतिहास के पुनर्निर्माण के लिए आनुवंशिक दूरी उपयोगी है, जैसे कि अफ्रीका सिद्धांत के बाहर कई मानव विस्तार। इसका उपयोग जैव विविधता की उत्पत्ति को समझने के लिए भी किया जाता है। उदाहरण के लिए, पालतू जानवरों की विभिन्न नस्लों के बीच आनुवंशिक दूरी की अक्सर जांच की जाती है ताकि यह निर्धारित किया जा सके कि आनुवंशिक विविधता को बनाए रखने के लिए किन नस्लों को संरक्षित किया जाना चाहिए।

जैविक नींव

एक जीव के जीनोम में, प्रत्येक जीन एक विशिष्ट स्थान पर स्थित होता है जिसे उस जीन के लिए लोकस (आनुवांशिकी) कहा जाता है। इन लोकी में युग्मक भिन्नता प्रजातियों के भीतर फेनोटाइपिक भिन्नता का कारण बनती है (जैसे बालों का रंग, आंखों का रंग)। हालांकि, अधिकांश एलील्स का फेनोटाइप पर कोई प्रभाव नहीं पड़ता है। आबादी के भीतर उत्परिवर्तन द्वारा उत्पन्न नए एलील या तो मर जाते हैं या पूरी आबादी में फैल जाते हैं। जब एक आबादी को अलग-अलग अलग-अलग आबादी में विभाजित किया जाता है (भौगोलिक या पारिस्थितिक कारकों द्वारा), विभाजन के बाद होने वाले उत्परिवर्तन केवल पृथक आबादी में मौजूद होंगे। एलील फ़्रीक्वेंसी का यादृच्छिक उतार-चढ़ाव भी आबादी के बीच आनुवंशिक भेदभाव पैदा करता है। इस प्रक्रिया को आनुवंशिक बहाव के रूप में जाना जाता है। आबादी और कंप्यूटिंग आनुवंशिक दूरी के बीच एलील आवृत्तियों के बीच अंतर की जांच करके, हम अनुमान लगा सकते हैं कि कितनी देर पहले दो आबादी अलग हो गई थी।

उपाय

यद्यपि आनुवंशिक दूरी को आनुवंशिक विचलन के माप के रूप में परिभाषित करना सरल है, फिर भी कई अलग-अलग सांख्यिकीय उपाय प्रस्तावित किए गए हैं। ऐसा इसलिए हुआ है क्योंकि अलग-अलग लेखकों ने अलग-अलग विकासवादी मॉडल पर विचार किया। सबसे अधिक इस्तेमाल किया जाने वाला नी की आनुवंशिक दूरी है,कवेली-स्फोर्ज़ा और एडवर्ड्स माप, और रेनॉल्ड्स, वीर और कॉकरहम आनुवंशिक दूरी, नीचे दिये गये।

इस खंड के सभी सूत्रों में, $X$ और $Y$ जिसके लिए दो अलग-अलग आबादी का प्रतिनिधित्व करते हैं $L$ लोकी का अध्ययन किया गया है। होने देना $X_{u}$ प्रतिनिधित्व करते हैं $u$^वें एलील फ्रीक्वेंसी पर $l$^वें ठिकाना।

Nei की मानक आनुवंशिक दूरी

1972 में, मसातोशी नेई ने प्रकाशित किया जिसे नेई की मानक आनुवंशिक दूरी के रूप में जाना जाने लगा। इस दूरी का यह अच्छा गुण है कि यदि प्रति वर्ष या पीढ़ी में आनुवंशिक परिवर्तन (अमीनो एसिड प्रतिस्थापन) की दर स्थिर रहती है तो Nei की मानक आनुवंशिक दूरी (D) विचलन समय के अनुपात में बढ़ जाती है। यह उपाय मानता है कि आनुवंशिक अंतर उत्परिवर्तन और आनुवंशिक बहाव के कारण होता है।

$D=-\ln {\frac {\sum \limits _{\ell }\sum \limits _{u}X_{u}Y_{u}}{\sqrt {\left(\sum \limits _{u}X_{u}^{2}\right)\left(\sum \limits _{u}Y_{u}^{2}\right)}}}$

यह दूरी जीन पहचान के अंकगणितीय माध्य के संदर्भ में भी व्यक्त की जा सकती है। होने देना $j_{X}$ जनसंख्या के दो सदस्यों के लिए संभावना हो $X$ एक विशेष स्थान पर एक ही एलील होना और $j_{Y}$ जनसंख्या में संगत संभावना हो $Y$. इसके अलावा, चलो $j_{XY}$ के एक सदस्य के लिए संभावना हो $X$ और का एक सदस्य $Y$ एक ही एलील होना। अब चलो $J_{X}$, $J_{Y}$ और $J_{XY}$ के अंकगणितीय माध्य का प्रतिनिधित्व करते हैं $j_{X}$, $j_{Y}$ और $j_{XY}$ सभी लोकी पर, क्रमशः। दूसरे शब्दों में,

$J_{X}=\sum _{u}{\frac {{X_{u}}^{2}}{L}}$

$J_{Y}=\sum _{u}{\frac {{Y_{u}}^{2}}{L}}$

$J_{XY}=\sum _{\ell }\sum _{u}{\frac {X_{u}Y_{u}}{L}}$

कहाँ $L$ लोकी की जांच की कुल संख्या है। Nei की मानक दूरी को तब इस प्रकार लिखा जा सकता है

$D=-\ln {\frac {J_{XY}}{\sqrt {J_{X}J_{Y}}}}$

कवेली-स्फोर्ज़ा तार दूरी

1967 में लुइगी लुका कवेली-स्फोर्ज़ा और ए.डब्ल्यू.एफ. एडवर्ड्स ने इस उपाय को प्रकाशित किया। यह मानता है कि अनुवांशिक मतभेद केवल अनुवांशिक बहाव के कारण उत्पन्न होते हैं। इस उपाय का एक प्रमुख लाभ यह है कि आबादी को हाइपरस्फीयर में दर्शाया जाता है, जिसका पैमाना प्रति जीन प्रतिस्थापन एक इकाई है। हाइपरडिमेंशनल स्फीयर में जीवा की दूरी किसके द्वारा दी जाती है

$D_{\text{CH}}={\frac {2}{\pi }}{\sqrt {2\left(1-\sum _{\ell }\sum _{u}{\sqrt {X_{u}Y_{u}}}\right)}}$

कुछ लेखक कारक छोड़ देते हैं ${\frac {2}{\pi }}$ संपत्ति को खोने की कीमत पर सूत्र को सरल बनाने के लिए कि पैमाना एक इकाई प्रति जीन प्रतिस्थापन है।

रेनॉल्ड्स, वीर, और कॉकरहम की आनुवंशिक दूरी

1983 में, इस माप को जॉन रेनॉल्ड्स, ब्रूस वीर और सी. क्लार्क कॉकरहैम द्वारा प्रकाशित किया गया था। यह उपाय मानता है कि अनुवांशिक भिन्नता उत्परिवर्तन के बिना अनुवांशिक बहाव से ही होती है। यह मैलेकोट की सहवंश की विधि का अनुमान लगाता है $\Theta$ जो अनुवांशिक विचलन का एक उपाय प्रदान करता है:

$\Theta _{w}={\sqrt {\frac {\sum \limits _{\ell }\sum \limits _{u}(X_{u}-Y_{u})^{2}}{2\sum \limits _{\ell }\left(1-\sum \limits _{u}X_{u}Y_{u}\right)}}}$

अन्य उपाय

अलग-अलग सफलता के साथ आनुवंशिक दूरी के कई अन्य उपाय प्रस्तावित किए गए हैं।

नया डी_A दूरी 1983

यह दूरी मानती है कि उत्परिवर्तन और आनुवंशिक बहाव के कारण आनुवंशिक अंतर उत्पन्न होते हैं, लेकिन यह दूरी माप विशेष रूप से माइक्रोसेटेलाइट डीएनए डेटा के लिए अन्य दूरियों की तुलना में अधिक विश्वसनीय जनसंख्या वृक्ष देने के लिए जाना जाता है।

$D_{A}=1-\sum _{\ell }\sum _{u}{\sqrt {X_{u}Y_{u}}}/{L}$

यूक्लिडियन दूरी

दुनिया भर में 51 मानव आबादी के बीच यूक्लिडियन आनुवंशिक दूरी, 289,160 एसएनपी का उपयोग करके गणना की गई। गहरा लाल सबसे समान जोड़ी है और गहरा नीला सबसे दूर का जोड़ा है।

Main article: Euclidean distance

$D_{EU}={\sqrt {\sum _{u}(X_{u}-Y_{u})^{2}}}$

गोल्डस्टीन दूरी 1995

यह विशेष रूप से माइक्रोसैटेलाइट मार्करों के लिए विकसित किया गया था और यह स्टेपवाइज म्यूटेशन मॉडल | स्टेपवाइज-म्यूटेशन मॉडल (SMM) पर आधारित है। $\mu _{X}$ और $\mu _{Y}$ जनसंख्या X और Y में एलील आकार के साधन हैं।

$(\delta \mu )^{2}=\sum _{\ell }{\frac {(\mu _{X}-\mu _{Y})^{2}}{L}}$

Nei की न्यूनतम अनुवांशिक दूरी 1973

यह उपाय मानता है कि उत्परिवर्तन और अनुवांशिक बहाव के कारण अनुवांशिक मतभेद उत्पन्न होते हैं।

$D_{m}={\frac {J_{X}+J_{Y}}{2}}-J_{XY}$

रोजर की दूरी 1972

$D_{R}={\frac {1}{L}}{\sqrt {\frac {\sum \limits _{u}(X_{u}-Y_{u})^{2}}{2}}}$

फिक्सेशन इंडेक्स

Main article: Fixation index

अनुवांशिक दूरी का आमतौर पर इस्तेमाल किया जाने वाला माप निर्धारण सूचकांक (एफ_ST) जो 0 और 1 के बीच भिन्न होता है। 0 का मान इंगित करता है कि दो आबादी आनुवंशिक रूप से समान हैं (दो आबादी के बीच न्यूनतम या कोई आनुवंशिक विविधता नहीं है) जबकि 1 का मान इंगित करता है कि दो आबादी आनुवंशिक रूप से भिन्न हैं (दो आबादी के बीच अधिकतम आनुवंशिक विविधता) ). कोई उत्परिवर्तन नहीं माना जाता है। बड़ी आबादी, जिनके बीच बहुत अधिक प्रवासन होता है, उदाहरण के लिए, थोड़ा अलग होने की प्रवृत्ति होती है, जबकि छोटी आबादी जिनके बीच बहुत कम प्रवास होता है, उनमें बहुत अंतर होता है। एफ_ST इस भेदभाव का एक सुविधाजनक उपाय है, और परिणामस्वरूप एफ_ST और संबंधित आँकड़े जनसंख्या और विकासवादी आनुवंशिकी में सबसे व्यापक रूप से उपयोग किए जाने वाले वर्णनात्मक आंकड़ों में से हैं। लेकिन एफ_ST एक वर्णनात्मक आंकड़े और अनुवांशिक भेदभाव के उपाय से अधिक है। एफ_ST आबादी के बीच एलील आवृत्ति में भिन्नता से सीधे संबंधित है और इसके विपरीत आबादी के भीतर व्यक्तियों के बीच समानता की डिग्री है। अगर एफ_ST छोटा है, इसका मतलब है कि प्रत्येक आबादी के भीतर एलील आवृत्तियां बहुत समान हैं; यदि यह बड़ा है, तो इसका मतलब है कि एलील फ़्रीक्वेंसी बहुत अलग हैं।

सॉफ्टवेयर

• PHYLIP उपयोग करता है GENDIST
  • नेई की मानक आनुवंशिक दूरी 1972
  • कवेली-स्फोर्ज़ा और एडवर्ड्स 1967
  • रेनॉल्ड्स, वीर, और कॉकरहैम 1983
• TFPGA
  • Nei की मानक आनुवंशिक दूरी (मूल और निष्पक्ष)
  • Nei की न्यूनतम आनुवंशिक दूरी (मूल और निष्पक्ष)
  • राइट्स (1978) रोजर्स (1972) की दूरी का संशोधन
  • रेनॉल्ड्स, वीर, और कॉकरहैम 1983
• GDA
• POPGENE
• POPTREE2 Takezaki, Nei, and Tamura (2010, 2014)
  • आमतौर पर इस्तेमाल की जाने वाली आनुवंशिक दूरी और जीन विविधता विश्लेषण
• DISPAN
  • नेई की मानक आनुवंशिक दूरी 1972
  • नेई का डी_A आबादी के बीच की दूरी 1983

यह भी देखें

• रिश्ते का गुणांक
• सगोत्रता की डिग्री
• मानव आनुवंशिक भिन्नता
• फाइलोजेनेटिक्स
• एलील आवृत्ति

बाहरी संबंध

• The Estimation of Genetic Distance and Population Substructure from Microsatellite allele frequency data., Brent W. Murray (May 1996), McMaster University website on genetic distance
• Computing distance by stepwise genetic distance model, web pages of Bruce Walsh at the Department of Ecology and Evolutionary Biology at the University of Arizona Archived 2006-12-10 at the Wayback Machine