फिटनेस परिदृश्य
| Part of a series on |
| Evolutionary biology |
|---|
 |
विकासवादी जीव विज्ञान में, फिटनेस परिदृश्य या अनुकूली परिदृश्य (विकासवादी परिदृश्य के प्रकार) का उपयोग जीनोटाइप और प्रजनन सफलता के बीच संबंधों को देखने के लिए किया जाता है। यह माना जाता है कि प्रत्येक जीनोटाइप में एक अच्छी तरह से परिभाषित प्रतिकृति दर होती है (जिसे अक्सर फिटनेस (जीव विज्ञान) कहा जाता है)। यह फिटनेस परिदृश्य की ऊंचाई है। जो जीनोटाइप समान हैं उन्हें एक-दूसरे के करीब कहा जाता है, जबकि जो बहुत अलग हैं वे एक-दूसरे से दूर हैं। सभी संभावित जीनोटाइप्स के सेट, उनकी समानता की डिग्री और उनके संबंधित फिटनेस मूल्यों को तब एक फिटनेस लैंडस्केप कहा जाता है। एक फिटनेस परिदृश्य का विचार प्राकृतिक चयन द्वारा विकास में खराब डिजाइन से तर्क की व्याख्या करने में मदद करने के लिए एक रूपक है, जिसमें जानवरों में शोषण और गड़बड़ी शामिल है, जैसे अलौकिक उत्तेजना के लिए उनकी प्रतिक्रिया।
एक प्रकार के परिदृश्य के रूप में फिटनेस मूल्यों के वितरण की कल्पना करके विकास का अध्ययन करने का विचार सबसे पहले 1932 में सेवल राइट द्वारा पेश किया गया था।[1] विकासवादी एल्गोरिथम समस्याओं में, फिटनेस परिदृश्य सभी उम्मीदवार समाधानों के लिए एक फिटनेस कार्य का मूल्यांकन है (नीचे देखें)।
जीव विज्ञान में
सभी फिटनेस परिदृश्यों में, ऊंचाई प्रतिनिधित्व करती है और फिटनेस (जीव विज्ञान) के लिए एक दृश्य रूपक है। अन्य आयामों को चित्रित करने के तीन अलग-अलग तरीके हैं, हालांकि प्रत्येक मामले में दूरी प्रतिनिधित्व करती है और असमानता की डिग्री के लिए एक रूपक है।[2]
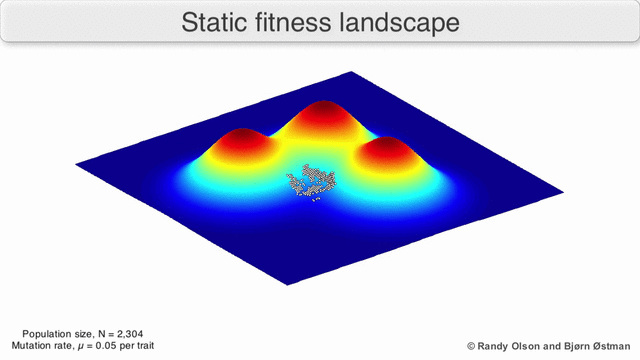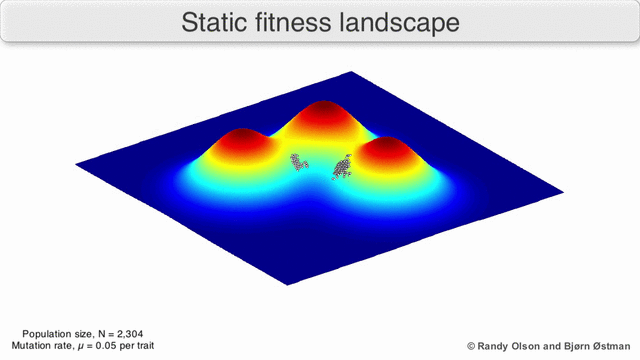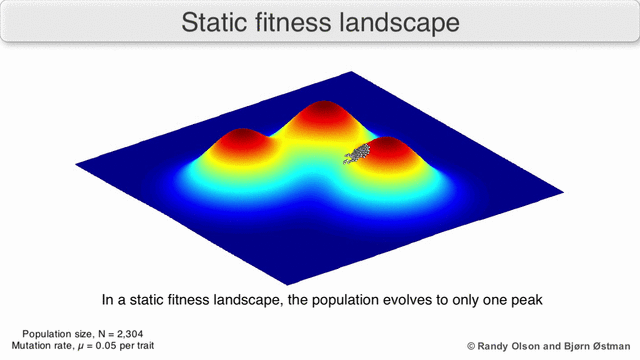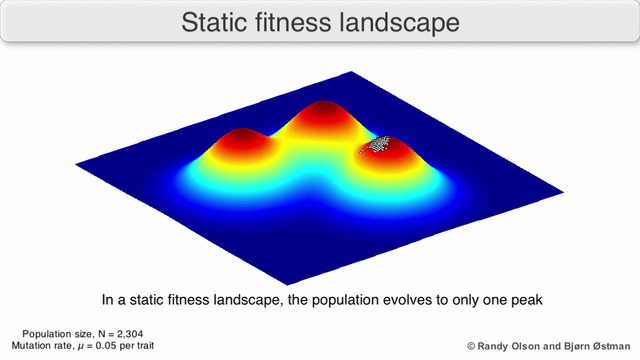
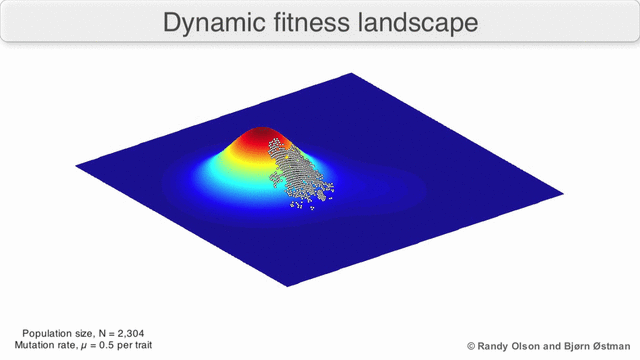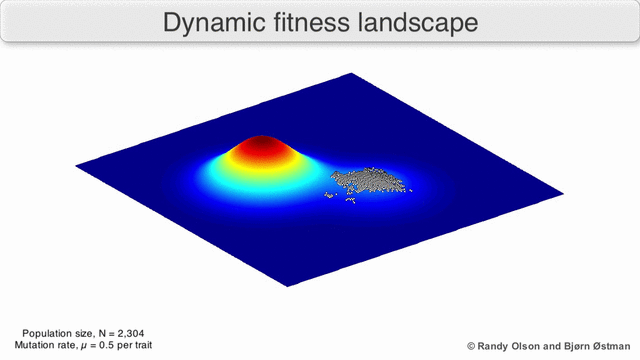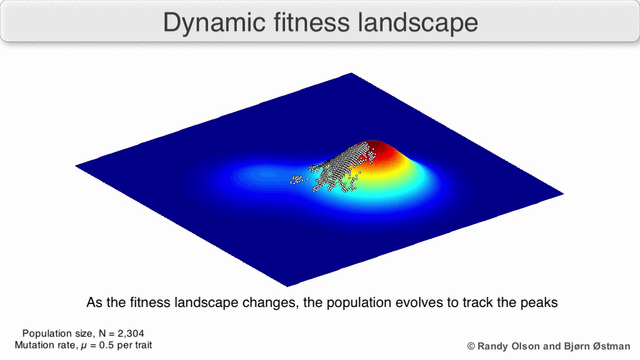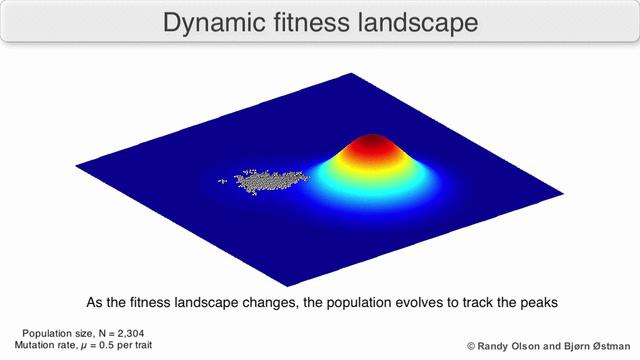
फ़िटनेस परिदृश्य की अक्सर पर्वत श्रृंखलाओं के रूप में कल्पना की जाती है. वहाँ स्थानीय चोटियाँ मौजूद हैं (वे बिंदु जहाँ से सभी रास्ते ढलान पर हैं, यानी कम फिटनेस के लिए) और घाटियाँ (ऐसे क्षेत्र जहाँ से कई रास्ते ऊपर की ओर जाते हैं)। गहरी घाटियों से घिरी कई स्थानीय चोटियों वाला एक फिटनेस परिदृश्य बीहड़ कहलाता है। यदि सभी जीनोटाइप समान प्रतिकृति दर है, दूसरी ओर, एक फिटनेस परिदृश्य को सपाट कहा जाता है। एक उभरती हुई आबादी आम तौर पर छोटे आनुवंशिक परिवर्तनों की एक श्रृंखला द्वारा फिटनेस परिदृश्य में ऊपर की ओर चढ़ती है, जब तक - अनंत समय सीमा में - एक स्थानीय इष्टतम तक नहीं पहुंच जाती।
ध्यान दें कि एक स्थानीय इष्टतम हमेशा विकासवादी समय में भी नहीं पाया जा सकता है: यदि स्थानीय इष्टतम को उचित समय में पाया जा सकता है तो फिटनेस परिदृश्य को आसान कहा जाता है और यदि आवश्यक समय घातीय है तो फिटनेस परिदृश्य को कठिन कहा जाता है।[3] कठोर भू-दृश्यों को भूलभुलैया जैसी संपत्ति की विशेषता होती है, जिसके द्वारा एक एलील जो एक बार फायदेमंद था, हानिकारक हो जाता है, विकास को पीछे हटने के लिए मजबूर करता है। हालांकि, जैव-भौतिक रूप से प्रेरित फिटनेस परिदृश्य में भूलभुलैया जैसी संपत्ति की उपस्थिति एक कठिन परिदृश्य उत्पन्न करने के लिए पर्याप्त नहीं हो सकती है।[4]

फिटनेस परिदृश्य के लिए जीनोटाइप
राइट ने एक जीनोटाइप स्पेस को अतिविम के रूप में देखा।[1]कोई निरंतर जीनोटाइप आयाम परिभाषित नहीं किया गया है। इसके बजाय, जीनोटाइप का एक नेटवर्क परस्पर पथ के माध्यम से जुड़ा हुआ है।
स्टुअर्ट कॉफ़मैन का एनके मॉडल फिटनेस परिदृश्य की इस श्रेणी में आता है। चयन-भारित आकर्षण रेखांकन (एसडब्ल्यूएजी) जैसी नई नेटवर्क विश्लेषण तकनीकें भी एक आयाम रहित जीनोटाइप स्थान का उपयोग करती हैं।[5]
फ़िटनेस लैंडस्केप के लिए एलील फ़्रीक्वेंसी
राइट के गणितीय कार्य ने फिटनेस को एलील आवृत्तियों के कार्य के रूप में वर्णित किया।[2]यहां, प्रत्येक आयाम एक अलग जीन पर एलील आवृत्ति का वर्णन करता है, और 0 और 1 के बीच जाता है।
फिटनेस परिदृश्य के लिए फेनोटाइप
तीसरे प्रकार के फिटनेस परिदृश्य में, प्रत्येक आयाम एक अलग फेनोटाइपिक विशेषता का प्रतिनिधित्व करता है।[2]मात्रात्मक आनुवंशिकी की मान्यताओं के तहत, इन फेनोटाइपिक आयामों को जीनोटाइप पर मैप किया जा सकता है। फेनोटाइप से फ़िटनेस लैंडस्केप के उदाहरणों के लिए नीचे दिए गए विज़ुअलाइज़ेशन देखें।
विकासवादी अनुकूलन में
विकासवादी जीव विज्ञान के क्षेत्र के अलावा, एक फिटनेस परिदृश्य की अवधारणा ने विकासवादी एल्गोरिदम विधियों जैसे आनुवंशिक एल्गोरिदम या विकास रणनीति में भी महत्व प्राप्त किया है। विकासवादी अनुकूलन में, जैविक विकास की गतिशीलता की नकल करके वास्तविक दुनिया की समस्याओं (जैसे, अभियांत्रिकी या रसद समस्याओं) को हल करने की कोशिश की जाती है। उदाहरण के लिए, कई गंतव्य पतों वाला एक डिलीवरी ट्रक विभिन्न मार्गों की एक बड़ी विविधता ले सकता है, लेकिन बहुत कम ड्राइविंग समय का परिणाम होगा।
विकासवादी अनुकूलन के कई सामान्य रूपों का उपयोग करने के लिए, किसी को ब्याज की समस्या के हर संभव समाधान बिंदु (यानी, डिलीवरी ट्रक के मामले में हर संभव मार्ग) को परिभाषित करना होगा कि यह कितना 'अच्छा' है। यह एक अदिश (गणित)-मूल्यवान फलन (गणित) f(s) को प्रस्तुत करके किया जाता है (अदिश मान का अर्थ है कि f(s) एक साधारण संख्या है, जैसे कि 0.3, जबकि s एक अधिक जटिल वस्तु हो सकती है, उदाहरण के लिए a डिलीवरी ट्रक के मामले में गंतव्य पतों की सूची), जिसे फिटनेस फ़ंक्शन कहा जाता है।
एक उच्च f(s) का अर्थ है कि s एक अच्छा समाधान है। डिलीवरी ट्रक के मामले में, f(s) रूट एस पर प्रति घंटे डिलीवरी की संख्या हो सकती है। सबसे अच्छा, या कम से कम एक बहुत अच्छा, समाधान तब निम्न तरीके से पाया जाता है: प्रारंभ में, यादृच्छिक समाधानों की आबादी बनाई जाती है। फिर, समाधान उत्परिवर्तित होते हैं और उच्च फिटनेस वाले लोगों के लिए चुने जाते हैं, जब तक कि एक संतोषजनक समाधान नहीं मिल जाता।
विकासवादी अनुकूलन तकनीक उन स्थितियों में विशेष रूप से उपयोगी होती है जिनमें एकल समाधान की गुणवत्ता निर्धारित करना आसान होता है, लेकिन एक-एक करके सभी संभावित समाधानों से गुजरना मुश्किल होता है (वितरण ट्रक के किसी विशेष मार्ग के लिए ड्राइविंग समय निर्धारित करना आसान होता है) , लेकिन एक बार गंतव्यों की संख्या मुट्ठी भर से अधिक हो जाने पर सभी संभावित मार्गों की जांच करना लगभग असंभव है)।
ऐसे मामलों में भी जहां एक फिटनेस फ़ंक्शन को परिभाषित करना कठिन है, फिटनेस परिदृश्य की अवधारणा उपयोगी हो सकती है। उदाहरण के लिए, यदि फिटनेस मूल्यांकन स्टोचैस्टिक नमूनाकरण द्वारा होता है, तो नमूना प्रत्येक बिंदु पर (आमतौर पर अज्ञात) वितरण से होता है; फिर भी प्रत्येक बिंदु पर अपेक्षित फिटनेस द्वारा निर्मित परिदृश्य के बारे में तर्क करना उपयोगी हो सकता है। यदि फिटनेस समय के साथ बदलती है (गतिशील अनुकूलन) या पर्यावरण में अन्य प्रजातियों के साथ (सह-विकास), यह अभी भी तात्कालिक फिटनेस परिदृश्य के प्रक्षेपवक्र के बारे में तर्क करने के लिए उपयोगी हो सकता है। हालांकि, कुछ मामलों में (उदाहरण के लिए, वरीयता-आधारित इंटरैक्टिव विकासवादी संगणना) प्रासंगिकता अधिक सीमित है, क्योंकि इस बात की कोई गारंटी नहीं है कि मानव वरीयताएँ एकल फिटनेस असाइनमेंट के अनुरूप हैं।
स्केलर मूल्यवान फिटनेस फ़ंक्शन एफ (एस) की अवधारणा भी भौतिकी में संभावित या ऊर्जा समारोह की अवधारणा से मेल खाती है। दो अवधारणाएं केवल इस बात में भिन्न हैं कि भौतिकविद पारंपरिक रूप से संभावित कार्य को कम करने के संदर्भ में सोचते हैं, जबकि जीवविज्ञानी इस धारणा को पसंद करते हैं कि फिटनेस को अधिकतम किया जा रहा है। इसलिए, एक संभावित फ़ंक्शन का व्युत्क्रम लेने से यह एक फिटनेस फ़ंक्शन में बदल जाता है, और इसके विपरीत।[6]
चेतावनियां और सीमाएं
कई महत्वपूर्ण चेतावनियां मौजूद हैं। चूंकि मानव मन तीन आयामों से अधिक सोचने के लिए संघर्ष करता है, इसलिए 3डी टोपोलॉजी अत्यधिक बहुआयामी फिटनेस परिदृश्यों पर चर्चा करते समय गुमराह कर सकती है।[7][8] विशेष रूप से यह स्पष्ट नहीं है कि क्या प्राकृतिक जैविक फिटनेस परिदृश्यों में चोटियों को ऐसे बहुआयामी परिदृश्यों में फिटनेस घाटियों द्वारा वास्तव में अलग किया गया है, या क्या वे बहुत लंबी तटस्थ लकीरों से जुड़े हुए हैं।[9][10] इसके अतिरिक्त, फिटनेस परिदृश्य समय के साथ स्थिर नहीं है बल्कि बदलते परिवेश और अन्य जीनों के विकास पर निर्भर है।[5]इसलिए यह एक सीस्केप का अधिक है,[11] आगे यह प्रभावित करता है कि अलग-अलग अनुकूली शिखर वास्तव में कैसे हो सकते हैं। इसके अतिरिक्त, यह ध्यान रखना प्रासंगिक है कि एक परिदृश्य सामान्य रूप से एक पूर्ण नहीं बल्कि एक सापेक्ष कार्य है।[12] अंत में, चूंकि एंजाइमों पर चर्चा करते समय फिटनेस के लिए एक प्रॉक्सी के रूप में फ़ंक्शन का उपयोग करना आम है, कोई भी अनैतिक गतिविधियां अतिव्यापी परिदृश्य के रूप में मौजूद होती हैं जो एक साथ जीव की अंतिम फिटनेस का निर्धारण करती हैं, जो विभिन्न सह-अस्तित्व वाले सापेक्ष परिदृश्यों के बीच अंतर को दर्शाती हैं।[13] इन सीमाओं को ध्यान में रखते हुए, फिटनेस परिदृश्य अभी भी विकास के बारे में सोचने का एक शिक्षाप्रद तरीका हो सकता है। लैंडस्केप कठोरता और शिखर संख्या, ऊंचाई, अलगाव और क्लस्टरिंग के कुछ मानकों को मापना (भले ही कल्पना न करना हो) मौलिक रूप से संभव है। इसके बाद सरलीकृत 3डी भूदृश्यों को संबंधित विशेषताओं को दृष्टिगत रूप से प्रस्तुत करने के लिए एक दूसरे के सापेक्ष उपयोग किया जा सकता है। इसके अतिरिक्त, विकासवादी मार्गों के छोटे उपसमुच्चय के फिटनेस परिदृश्य प्रयोगात्मक रूप से निर्मित और देखे जा सकते हैं, संभावित रूप से फिटनेस चोटियों और घाटियों जैसी सुविधाओं का खुलासा कर सकते हैं।[5]विकासवादी मार्गों के स्वास्थ्य परिदृश्य संभावित विकासवादी कदमों और अलग-अलग उत्परिवर्तनों के सेट के बीच समापन बिंदुओं को इंगित करते हैं।
यह भी देखें
संदर्भ
- ↑ 1.0 1.1 Wright, Sewall (1932). "विकास में उत्परिवर्तन, अंतःप्रजनन, क्रॉसब्रीडिंग और चयन की भूमिका" (PDF). Proceedings of the Sixth International Congress on Genetics. 1 (8): 355–66.
- ↑ 2.0 2.1 2.2 Provine, William B. (1986). सीवेल राइट एंड इवोल्यूशनरी बायोलॉजी. University of Chicago Press.[page needed]
- ↑ Kaznatcheev, Artem (2019). "विकास पर एक अंतिम बाधा के रूप में कम्प्यूटेशनल जटिलता". Genetics. 212 (1): 245–265. doi:10.1534/genetics.119.302000. PMC 6499524. PMID 30833289.
- ↑ Bertram, Jason; Masel, Joanna (April 2020). "विकास तेजी से व्यापक लैंडस्केप घाटियों और भूल-भुलैया के बावजूद जाली प्रोटीन में स्थिरता और एकत्रीकरण का अनुकूलन करता है". Genetics. 214 (4): 1047–1057. doi:10.1534/genetics.120.302815. PMC 7153934. PMID 32107278.
- ↑ 5.0 5.1 5.2 Steinberg, B; Ostermeier, M (2016). "पर्यावरण परिवर्तन विकासवादी घाटियों को पाटते हैं". Science Advances. 2 (1): e1500921. Bibcode:2016SciA....2E0921S. doi:10.1126/sciadv.1500921. PMC 4737206. PMID 26844293.
- ↑ Kauffman, Stuart A. (1993). आदेश की उत्पत्ति, स्व-संगठन और विकास में चयन (1st ed.). New york - Oxford: Oxford University Press. p. 43. ISBN 0-19-505811-9.
- ↑ McCandlish, David M (2011). "स्वास्थ्य परिदृश्य की कल्पना करना". Evolution. 65 (6): 1544–58. doi:10.1111/j.1558-5646.2011.01236.x. PMC 3668694. PMID 21644947.
- ↑ McGhee, George R. (2006). The Geometry of Evolution: Adaptive Landscapes and Theoretical Morphospaces. ISBN 978-1-139-45995-2.[page needed]
- ↑ Gavrilets, S. (2004). स्वास्थ्य परिदृश्य और प्रजातियों की उत्पत्ति. Princeton University Press. ISBN 978-0-691-11983-0.[page needed]
- ↑ Kaplan, Jonathan (2008). "The end of the adaptive landscape metaphor?". Biology & Philosophy. 23 (5): 625–38. doi:10.1007/s10539-008-9116-z. S2CID 170649453.
- ↑ Mustonen, Ville; Lässig, Michael (2009). "From fitness landscapes to seascapes: Non-equilibrium dynamics of selection and adaptation". Trends in Genetics. 25 (3): 111–9. doi:10.1016/j.tig.2009.01.002. PMID 19232770.
- ↑ Woodcock, Glenn; Higgs, Paul G (1996). "मल्टीप्लिकेटिव सिंगल-पीक फिटनेस लैंडस्केप पर जनसंख्या विकास". Journal of Theoretical Biology. 179 (1): 61–73. doi:10.1006/jtbi.1996.0049. PMID 8733432.
- ↑ Diaz Ochoa, Juan G (2017). "Elastic Multi-scale Mechanisms: Computation and Biological Evolution". Journal of Molecular Evolution. 86 (1): 47–57. Bibcode:2018JMolE..86...47D. doi:10.1007/s00239-017-9823-7. PMID 29248946. S2CID 22624633.
बाहरी संबंध
- Examples of visualized fitness landscapes
- Video: Using fitness landscapes to visualize evolution in action
- BEACON Blog—Evolution 101: Fitness Landscapes
- Pleiotropy Blog—an interesting discussion of Sergey Gavrilets's contributions
- Pup Fish Evolution—UC Davis
- Evolution 101—Shifting Balance Theory (Figure at bottom of page)
- Superimposing evolutionary trajectories onto fitness landscapes in virtual reality
- Further reading
- Counterbalance: Evolution as movement through a fitness landscape—an interesting (if flawed) discussion of evolution and fitness landscapes
- Example of the use of Evolutionary Landscapes in thinking & speaking about evolution
- Hendrik Richter; Andries P. Engelbrecht (2014). Recent Advances in the Theory and Application of Fitness Landscapes. ISBN 978-3-642-41888-4.
- Beerenwinkel, Niko; Pachter, Lior; Sturmfels, Bernd (2007). "Epistasis and Shapes of Fitness Landscapes". Statistica Sinica. 17 (4): 1317–42. arXiv:q-bio.PE/0603034. Bibcode:2006q.bio.....3034B. MR 2398598.
- Richard Dawkins (1996). Climbing Mount Improbable. ISBN 0-393-03930-7.
- Sergey Gavrilets (2004). Fitness landscapes and the origin of species. ISBN 978-0-691-11983-0.
- Stuart Kauffman (1995). At Home in the Universe: The Search for Laws of Self-Organization and Complexity. ISBN 978-0-19-511130-9.
- Melanie Mitchell (1996). An Introduction to Genetic Algorithms (PDF). ISBN 978-0-262-63185-3.
- Langdon, W. B.; Poli, R. (2002). "Chapter 2 Fitness Landscapes". Foundations of Genetic Programming. ISBN 3-540-42451-2.
- Stuart Kauffman (1993). The Origins of Order. ISBN 978-0-19-507951-7.
- Poelwijk, Frank J; Kiviet, Daniel J; Weinreich, Daniel M; Tans, Sander J (2007). "Empirical fitness landscapes reveal accessible evolutionary paths". Nature. 445 (7126): 383–6. Bibcode:2007Natur.445..383P. doi:10.1038/nature05451. PMID 17251971. S2CID 4415468.