काल्पनिक न्यायवाक्य

Hypothetical syllogism

Type	Syllogism
Field	Propositional calculus Classical logic Intuitionistic logic Most systems of relevance logic
Statement	Whenever instances of $P\to Q$, and $Q\to R$ appear on lines of a proof, $P\to R$ can be placed on a subsequent line.
Symbolic statement	${\frac {P\to Q,Q\to R}{\therefore P\to R}}$

शास्त्रीय तर्क में, एक काल्पनिक न्यायवाक्य एक वैध तर्क रूप है, एक या दोनों परिसरों के लिए एक सशर्त कथन के साथ एक न्यायवाक्य।

काल्पनिक न्यायवाक्य के चार संभावित रूप हैं, जिनमें से दो वैध हैं, जबकि दो अमान्य हैं। एक बहुत ही सरल उदाहरण पर विचार करने से आपको यह समझने में मदद मिल सकती है कि ये फॉर्म वैध या अमान्य क्यों हैं। यदि p दर्शाता है कि कैंडिरू एक मछली है और q दर्शाता है कि कैंडिरू में गलफड़े हैं, तो उपरोक्त तालिका में इन कथनों को p और q से प्रतिस्थापित करके स्वयं को समझाने का प्रयास करें।

अंग्रेजी भाषा में एक उदाहरण:

अगर मैं नहीं जागा, तो मैं काम पर नहीं जा पाऊंगा.

अगर मैं काम पर नहीं जा सकता तो मुझे वेतन नहीं मिलेगा।

इसलिए, अगर मैं नहीं जागा, तो मुझे भुगतान नहीं मिलेगा।

इस शब्द की उत्पत्ति ठेओफ्रस्तुस से हुई। शुद्ध काल्पनिक न्यायवाक्य वह न्यायवाक्य है जिसमें परिसर और निष्कर्ष दोनों सशर्त होते हैं। सशर्त वैध होने के लिए एक आधार का पूर्ववृत्त दूसरे के परिणाम से मेल खाना चाहिए। नतीजतन, सशर्त पूर्ववर्ती के रूप में पूर्ववर्ती बने रहे और परिणामी के रूप में परिणामी बने रहे।

यदि p, तो q.

यदि q, तो r.

∴ यदि p, तो r.

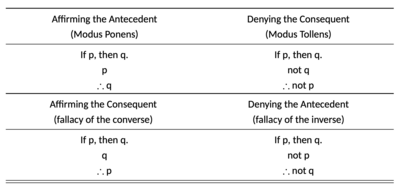
एक मिश्रित काल्पनिक न्यायवाक्य में एक सशर्त कथन और एक कथन शामिल होता है जो उस सशर्त के पूर्ववृत्त या परिणाम के साथ या तो पुष्टि या खंडन व्यक्त करता है। इसलिए, ऐसे मिश्रित काल्पनिक न्यायवाक्य के चार संभावित रूप हैं, जिनमें से दो वैध हैं, जबकि अन्य दो अमान्य हैं (तालिका देखें)। वैध निष्कर्ष प्राप्त करने का पहला तरीका पूर्ववृत्त की पुष्टि करना है। एक वैध काल्पनिक न्यायवाक्य या तो परिणामी (मोडस टोलेंस) को नकारता है या पूर्ववर्ती (मोडस पोनेंस) की पुष्टि करता है।

प्रस्तावात्मक तर्क

प्रस्तावात्मक तर्क में, काल्पनिक न्यायवाक्य अनुमान के एक वैध नियम का नाम है (अक्सर संक्षिप्त एचएस और कभी-कभी श्रृंखला तर्क, श्रृंखला नियम, या निहितार्थ की परिवर्तनशीलता का सिद्धांत भी कहा जाता है)। नियम कहा जा सकता है:

${\frac {P\to Q,Q\to R}{\therefore P\to R}}$

जहां नियम यह है कि जब भी उदाहरण हों$P\to Q$, और$Q\to R$एक औपचारिक प्रमाण की तर्ज पर प्रकट होते हैं,$P\to R$अगली पंक्ति में रखा जा सकता है.

हाइपोथेटिकल सिलोगिज्म निकटता से संबंधित है और विच्छेदात्मक न्यायवाक्य के समान है, इसमें यह एक प्रकार का सिलोगिज्म भी है, और अनुमान के नियम का नाम भी है।

प्रयोज्यता

काल्पनिक न्यायशास्त्र का नियम शास्त्रीय तर्क, अंतर्ज्ञानवादी तर्क, प्रासंगिक तर्क की अधिकांश प्रणालियों और तर्क की कई अन्य प्रणालियों में लागू होता है। हालाँकि, यह सभी तर्कों पर लागू नहीं होता है, उदाहरण के लिए, गैर-मोनोटोनिक तर्क, संभाव्य तर्क और डिफ़ॉल्ट तर्क। इसका कारण यह है कि ये तर्क अक्षम्य तर्क का वर्णन करते हैं, और वास्तविक दुनिया के संदर्भों में दिखाई देने वाली सशर्तताएं आम तौर पर अपवादों, डिफ़ॉल्ट मान्यताओं, अन्य सभी समान स्थितियों या बस साधारण अनिश्चितता की अनुमति देती हैं।

अर्नेस्ट डब्ल्यू एडम्स से लिया गया एक उदाहरण,

1. यदि जोन्स चुनाव जीतता है, तो स्मिथ चुनाव के बाद सेवानिवृत्त हो जाएगा।
2. यदि चुनाव से पहले स्मिथ की मृत्यु हो जाती है, तो जोन्स चुनाव जीत जाएगा।
3. यदि चुनाव से पहले स्मिथ की मृत्यु हो जाती है, तो चुनाव के बाद स्मिथ सेवानिवृत्त हो जायेंगे.

स्पष्टतः, (3) (1) और (2) से अनुसरण नहीं करता है। (1) डिफ़ॉल्ट रूप से सत्य है, लेकिन स्मिथ की मृत्यु की असाधारण परिस्थितियों में इसे लागू करने में विफल रहता है। व्यवहार में, वास्तविक दुनिया की सशर्तताओं में हमेशा डिफ़ॉल्ट धारणाएं या संदर्भ शामिल होते हैं, और उन सभी असाधारण परिस्थितियों को निर्दिष्ट करना असंभव या यहां तक ​​​​कि असंभव हो सकता है जिनमें वे सत्य होने में विफल हो सकते हैं। समान कारणों से, काल्पनिक न्यायवाक्य का नियम प्रतितथ्यात्मक शर्तों पर लागू नहीं होता है।

औपचारिक संकेतन

काल्पनिक न्यायवाक्य अनुमान नियम को अनुक्रमिक संकेतन में लिखा जा सकता है, जो कट नियम की विशेषज्ञता के समान है:

${\frac {P\vdash Q\quad Q\vdash R}{P\vdash R}}$

कहाँ $\vdash$ एक धातु प्रतीक है और $A\vdash B$ मतलब है कि $B$ का तार्किक परिणाम है $A$ कुछ औपचारिक प्रणाली में;

और एक सत्य-कार्यात्मक टॉटोलॉजी (तर्क) या प्रस्तावात्मक कलन के प्रमेय के रूप में व्यक्त किया गया:

$((P\to Q)\land (Q\to R))\to (P\to R)$

कहाँ $P$, $Q$, और $R$ कुछ औपचारिक प्रणाली में व्यक्त किए गए प्रस्ताव हैं।

प्रमाण

Step	Proposition	Derivation
1	$P\to Q$	Given
2	$Q\to R$	Given
3	$P$	Conditional proof assumption
4	$Q$	Modus ponens (1,3)
5	$R$	Modus ponens (2,4)
6	$P\to R$	Conditional Proof (3-5)

वैकल्पिक रूप

काल्पनिक न्यायवाक्य का एक वैकल्पिक रूप, List_of_Hilbert_systems#Classical_propositional_calculus_systems के लिए निहितार्थ और निषेध के साथ अधिक उपयोगी (अर्थात संयोजन चिह्न के बिना), निम्नलिखित है:

(HS1) $(Q\to R)\to ((P\to Q)\to (P\to R))$

फिर भी एक और रूप है:

(HS2) $(P\to Q)\to ((Q\to R)\to (P\to R))$

प्रमाण

ऐसी प्रणालियों में इन प्रमेयों के प्रमाण का एक उदाहरण नीचे दिया गया है। हम Jan Łukasiewicz द्वारा वर्णित Propositional_calculus#Example_1._Simple_axiom_system में उपयोग किए गए तीन सिद्धांतों में से दो का उपयोग करते हैं। प्रमाण इस प्रणाली के तीन सिद्धांतों में से दो पर निर्भर करते हैं:

(ए1) $\phi \to \left(\psi \to \phi \right)$

(आआ) $\left(\phi \to \left(\psi \rightarrow \xi \right)\right)\to \left(\left(\phi \to \psi \right)\to \left(\phi \to \xi \right)\right)$

(HS1) का प्रमाण इस प्रकार है:

(1) $((p\to (q\to r))\to ((p\to q)\to (p\to r)))\to ((q\to r)\to ((p\to (q\to r))\to ((p\to q)\to (p\to r))))$ ((A1) का उदाहरण)

(2) $(p\to (q\to r))\to ((p\to q)\to (p\to r))$ ((A2 का उदाहरण))

(3) $(q\to r)\to ((p\to (q\to r))\to ((p\to q)\to (p\to r)))$ (सेटिंग विधि द्वारा (1) और (2) से)

(4) $((q\to r)\to ((p\to (q\to r))\to ((p\to q)\to (p\to r))))\to (((q\to r)\to (p\to (q\to r)))\to ((q\to r)\to ((p\to q)\to (p\to r))))$ ((A2 का उदाहरण))

(5) $((q\to r)\to (p\to (q\to r)))\to ((q\to r)\to ((p\to q)\to (p\to r)))$ (सेटिंग विधि द्वारा (3) और (4) से)

(6) $(q\to r)\to (p\to (q\to r))$ ((A1) का उदाहरण)

(7) $(q\to r)\to ((p\to q)\to (p\to r))$ ((5) और (6) से मोडस पोनेन्स द्वारा)

(HS2) का प्रमाण हिल्बर्ट_सिस्टम#कुछ_उपयोगी_प्रमेय_और_उनके_प्रमाण दिए गए हैं।

एक मेटाथ्योरम के रूप में

जब भी हमारे पास फॉर्म के दो प्रमेय होते हैं $T_{1}=(Q\to R)$ और $T_{2}=(P\to Q)$, हम साबित कर सकते हैं $(P\to R)$ निम्नलिखित चरणों द्वारा:

(1) $(Q\to R)\to ((P\to Q)\to (P\to R)))$ (ऊपर सिद्ध प्रमेय का उदाहरण)

(2) $Q\to R$ ((T1 का उदाहरण))

(3) $(P\to Q)\to (P\to R)$ (सेटिंग विधि द्वारा (1) और (2) से)

(4) $P\to Q$ ((T2 का उदाहरण))

(5) $P\to R$ (सेटिंग विधि द्वारा (3) और (4) से)

यह भी देखें

• मूड सेट करना
• हटाने की विधि
• परिणाम की पुष्टि करना
• पूर्ववृत्त को नकारना
• सकर्मक संबंध

बाहरी संबंध

• Philosophy Index: Hypothetical Syllogism