पुइसेक्स श्रृंखला
गणित में, पुइसेक्स श्रृंखला घात श्रृंखला का एक सामान्यीकरण है जो अनिश्चित (चर) के ऋणात्मक और भिन्नात्मक घातांक की अनुमति देती है। उदाहरण के लिए, श्रृंखला
अनिश्चित x में एक पुइसेक्स श्रृंखला होती है। पुइसेक्स श्रृंखला को पहली बार 1676 में आइजैक न्यूटन द्वारा प्रस्तुत किया गया था[1] और 1850 में विक्टर पुइसेक्स द्वारा पुनः खोजा गया था।[2]
पुइसेक्स श्रृंखला की परिभाषा में यह सम्मलित है कि घातांक के प्रत्येक को सीमित किया जाना चाहिए। तो, घातांक को एक सामान्य हर n तक कम करके, एक पुइसेक्स श्रृंखला अनिश्चित काल के nवें मूल में एक लॉरेंट श्रृंखला बन जाती है। उदाहरण के लिए, उपरोक्त उदाहरण लॉरेंट श्रृंखला होती है क्योंकि एक जटिल संख्या में n nवीं मूल होते हैं, एक अभिसरण श्रृंखला पुइसेक्स श्रृंखला सामान्यतः 0 के निकटतम में n फलन को परिभाषित करती है।
पुइसेक्स प्रमेय, जिसे कभी-कभी न्यूटन-पुइसेक्स प्रमेय भी कहा जाता है, यह प्रमाणित करता है कि, एक बहुपद समीकरण दिया गया है जटिल गुणांकों के साथ, इसके विलयन y, के फलनों के रूप में देखे जाने पर, x पुइसेक्स श्रृंखला के रूप में विस्तारित किया जा सकता है x जो कि 0 के कुछ निकटतम में अभिसरण होते हैं। दूसरे शब्दों में, बीजगणितीय वक्र की प्रत्येक शाखा को स्थानीय रूप से पुइसेक्स श्रृंखला द्वारा वर्णित किया जा सकता है x (या में x − x0 जब निकटतम के ऊपर की ब्रांच पर विचार किया जाता है x0 ≠ 0)
आधुनिक शब्दावली का उपयोग करते हुए, पुइसेक्स का प्रमेय प्रमाणित करता है कि विशेषता 0 के बीजगणितीय रूप से बंद क्षेत्र पर पुइसेक्स श्रृंखला का सेट स्वयं एक बीजगणितीय रूप से बंद क्षेत्र है, जिसे पुइसेक्स श्रृंखला का क्षेत्र कहा जाता है। यह औपचारिक घात श्रेणी औपचारिक लॉरेंट श्रृंखला का बीजगणितीय समापन है, जो स्वयं औपचारिक घात श्रेणी के वलय के अंशों का क्षेत्र होता है।
परिभाषा
यदि K एक क्षेत्र (जैसे जटिल संख्याएं) है, गुणांक के साथ एक पुइसेक्स श्रृंखला K रूप की अभिव्यक्ति है
कहाँ एक धनात्मक पूर्णांक है और पूर्णांक है दूसरे शब्दों में, पुइसेक्स श्रृंखला लॉरेंट श्रृंखला से इस मायने में भिन्न है कि वे अनिश्चित के भिन्नात्मक घातांक की अनुमति देते हैं, जब तक कि इन भिन्नात्मक घातांकों ने प्रत्येक (यहाँ n) को सीमित कर दिया है। लॉरेंट श्रृंखला की तरह, पुइसेक्स श्रृंखला अनिश्चित के ऋणात्मक घातांक के लिए अनुमति देती है जब तक कि ये ऋणात्मक घातांक नीचे (यहाँ द्वारा) सीमित हैं जोड़ और गुणा अपेक्षा के अनुरूप हैं: उदाहरण के लिए,
और
कोई पहले घातांक के हर को किसी सामान्य हर में अपग्रेड करके उन्हें परिभाषित कर सकता है, N और फिर औपचारिक लॉरेंट श्रृंखला के संबंधित क्षेत्र में ऑपरेशन निष्पादित करना
गुणांकों के साथ पुइसेक्स श्रृंखला K एक क्षेत्र बनाएं, जो संयोजन होता है
औपचारिक लॉरेंट श्रृंखला के क्षेत्रों में (अनिश्चित माना जाता है)।
इससे प्रत्यक्ष सीमा के संदर्भ में पुइसेक्स श्रृंखला के क्षेत्र की एक वैकल्पिक परिभाषा प्राप्त होती है। प्रत्येक सकारात्मक पूर्णांक के लिए n, होने देना एक अनिश्चित हो (प्रतिनिधित्व करने के लिए)। ), और औपचारिक लॉरेंट श्रृंखला का क्षेत्र बनें यदि m बांटता है n, मानचित्रण एक क्षेत्र समरूपता को प्रेरित करता है और ये समरूपताएं एक प्रत्यक्ष प्रणाली बनाती हैं जिसमें पुइसेक्स श्रृंखला का क्षेत्र प्रत्यक्ष सीमा के रूप में होता है। तथ्य यह है कि प्रत्येक क्षेत्र समरूपता अन्तःक्षेपण है, यह दर्शाता है कि इस प्रत्यक्ष सीमा को उपरोक्त संयोजन के साथ पहचाना जा सकता है, और यह कि दोनों परिभाषाएँ समतुल्य हैं (एक समरूपता तक)।
मूल्यांकन
एक शून्येतर पुइसेक्स श्रृंखला विशिष्ट रूप से लिखा जा सकता है
साथ मूल्यांकन
का परिमेय संख्याओं के प्राकृतिक क्रम और संगत गुणांक के लिए सबसे छोटा घातांक है का प्रारंभिक गुणांक या मूल्यांकन गुणांक कहा जाता है शून्य श्रृंखला का मूल्यांकन है कार्यक्रम v एक मूल्यांकन (बीजगणित) है और पुइसेक्स श्रृंखला को योगात्मक समूह के साथ एक मूल्यवान क्षेत्र बनाता है इसके मूल्यांकन समूह के रूप में तर्कसंगत संख्याएँ।
प्रत्येक मूल्यवान क्षेत्र के लिए, मूल्यांकन सूत्र द्वारा एक अल्ट्रामेट्रिक स्पेस को परिभाषित करता है इस दूरी के लिए, पुइसेक्स श्रृंखला का क्षेत्र एक मीट्रिक स्थान है। संकेतन
व्यक्त करता है कि एक पुइसेक्स उसके आंशिक योग की सीमा है। चूँकि, पुइसेक्स श्रृंखला का क्षेत्र पूर्ण मीट्रिक स्थान नहीं है; नीचे देखें § लेवी-सिविटा क्षेत्र.
अभिसरण पुइसेक्स श्रृंखला
- न्यूटन-पुइसेक्स प्रमेय द्वारा प्रदान की गई पुइसेक्स श्रृंखला न्यूटन-पुइसेक्स प्रमेय इस अर्थ में अभिसरण श्रृंखला है, कि शून्य का एक निकटतम है जिसमें वे अभिसरण हैं (यदि मूल्यांकन ऋणात्मक है तो 0 को बाहर रखा गया है)।
अधिक त्रुटिहीन रूप से, चलो
सम्मिश्र संख्या गुणांकों वाली एक पुइसेक्स श्रृंखला बनें। एक वास्तविक संख्या है r, जिसे अभिसरण की त्रिज्या कहा जाता है जैसे कि श्रृंखला अभिसरण करती है यदि T को एक गैरशून्य सम्मिश्र संख्या के लिए प्रतिस्थापित किया जाता है t निरपेक्ष मान से कम r, और r इस संपत्ति के साथ सबसे बड़ी संख्या है। एक पुइसेक्स श्रृंखला अभिसरण है यदि इसमें अभिसरण की गैर-शून्य त्रिज्या होता है।
क्योंकि एक शून्येतर सम्मिश्र संख्या होती है n nवाँ मूल nवें मूल, प्रतिस्थापन के लिए कुछ देखभाल की जानी चाहिए: एक विशिष्ट nकी मूल t, कहना x, चुना जाना चाहिए. फिर प्रतिस्थापन में प्रतिस्थापित करना सम्मलित है द्वारा हरएक के लिए k.
अभिसरण की त्रिज्या का अस्तित्व एक घात श्रेणी के लिए समान अस्तित्व से उत्पन्न होता है, जिस पर लागू होता है में एक घात श्रेणी के रूप में माना जाता है
यह न्यूटन-पुइसेक्स प्रमेय का एक हिस्सा है कि प्रदान की गई पुइसेक्स श्रृंखला में अभिसरण का एक सकारात्मक त्रिज्या है, और इस प्रकार शून्य के कुछ निकटतम में एक (बहुमूल्यवान फ़ंक्शन) विश्लेषणात्मक फ़ंक्शन को परिभाषित करता है (शून्य स्वयं संभवतः बाहर रखा गया है)।
गुणांकों पर मूल्यांकन और क्रम
यदि आधार क्षेत्र ऑर्डर किया गया क्षेत्र है, फिर पुइसेक्स श्रृंखला का क्षेत्र खत्म हो गया है इसे स्वाभाविक रूप से ("शब्दावली क्रम") निम्नानुसार क्रमबद्ध किया गया है: एक गैर-शून्य पुइसेक्स श्रृंखला जब भी इसका मूल्यांकन गुणांक ऐसा होता है तो 0 को सकारात्मक घोषित किया जाता है। अनिवार्य रूप से, इसका मतलब यह है कि अनिश्चित की कोई भी सकारात्मक तर्कसंगत शक्ति को सकारात्मक बनाया गया है, किन्तु आधार क्षेत्र में किसी भी सकारात्मक तत्व से छोटा है .
यदि आधार क्षेत्र मूल्यांकन से संपन्न है , तो हम पुइसेक्स श्रृंखला के क्षेत्र पर एक अलग मूल्यांकन का निर्माण कर सकते हैं मूल्यांकन देकर होना कहाँ पहले से परिभाषित मूल्यांकन है ( पहला गैर-शून्य गुणांक है) और असीम रूप से बड़ा है (दूसरे शब्दों में, का मान समूह है शब्दकोषीय ढंग से आदेश दिया गया, कहाँ का मान समूह है ). अनिवार्य रूप से, इसका मतलब है कि पहले से परिभाषित मूल्यांकन मूल्यांकन को ध्यान में रखने के लिए एक अनंत राशि द्वारा सही किया जाता है आधार क्षेत्र पर दिया गया है.
न्यूटन-पुइसेक्स प्रमेय
1671 की प्रारंभ में,[3] आइजैक न्यूटन ने स्पष्ट रूप से पुइसेक्स श्रृंखला का उपयोग किया और बीजगणितीय समीकरणों के एक फ़ंक्शन के शून्य को श्रृंखला (गणित) के साथ अनुमानित करने के लिए निम्नलिखित प्रमेय को प्रमाणित किया, जिनके गुणांक ऐसे कार्य हैं जो स्वयं श्रृंखला या बहुपद के साथ अनुमानित होते हैं। इस उद्देश्य के लिए, उन्होंने न्यूटन बहुभुज की प्रारंभ की, जो इस संदर्भ में एक मौलिक उपकरण बना हुआ है। न्यूटन ने संक्षिप्त श्रृंखला के साथ काम किया, और यह केवल 1850 में विक्टर पुइसेक्स द्वारा किया गया था[2] (गैर-काट-छाँट) पुइसेक्स श्रृंखला की अवधारणा प्रस्तुत की और उस प्रमेय को प्रमाणित किया जिसे अब पुइसेक्स प्रमेय या न्यूटन-पुइसेक्स प्रमेय के रूप में जाना जाता है।[4] प्रमेय का प्रमाणित है कि, एक बीजगणितीय समीकरण दिया गया है जिसके गुणांक बहुपद हैं या, अधिक सामान्यतः, विशेषता शून्य के क्षेत्र (गणित) पर पुइसेक्स श्रृंखला, समीकरण के प्रत्येक विलयन को पुइसेक्स श्रृंखला के रूप में व्यक्त किया जा सकता है। इसके अतिरिक्त, प्रमाण इन पुइसेक्स श्रृंखला की गणना के लिए एक एल्गोरिदम प्रदान करता है, और, जटिल संख्याओं पर काम करते समय, परिणामी श्रृंखला अभिसरण होती है।
आधुनिक शब्दावली में, प्रमेय को इस प्रकार दोहराया जा सकता है: विशेषता शून्य के क्षेत्र पर पुइसेक्स श्रृंखला का क्षेत्र, और जटिल संख्याओं पर अभिसरण पुइसेक्स श्रृंखला का क्षेत्र, दोनों बीजगणितीय रूप से बंद हैं।
न्यूटन बहुभुज
होने देना
एक बहुपद हो जिसका शून्येतर गुणांक हो बहुपद, घात श्रृंखला, या यहाँ तक कि पुइसेक्स श्रृंखला भी हैं x. इस खंड में, मूल्यांकन का का सबसे निचला घातांक है x में (इसमें से अधिकांश किसी भी मूल्यवान क्षेत्र में गुणांक पर अधिक सामान्यतः लागू होता है।)
पुइसेक्स श्रृंखला की गणना के लिए जो एक फ़ंक्शन के शून्य हैं P (यह कार्यात्मक समीकरण का विलयन है ), करने वाली पहली बात मूलों के मूल्यांकन की गणना करना है। यह न्यूटन बहुभुज की भूमिका है।
आइए, कार्तीय तल में, निर्देशांक के बिंदुओं पर विचार करें न्यूटन बहुभुज P इन बिंदुओं का निचला उत्तल आवरण है। अर्थात्, न्यूटन बहुभुज के किनारे इनमें से दो बिंदुओं को जोड़ने वाले रेखा खंड हैं, जैसे कि ये सभी बिंदु खंड का समर्थन करने वाली रेखा से नीचे नहीं हैं (नीचे, सामान्यतः, दूसरे निर्देशांक के मान के सापेक्ष होता है)।
पुइसेक्स श्रृंखला दी गई मूल्यांकन का , का मूल्यांकन कम से कम संख्याओं का न्यूनतम है और इस न्यूनतम के बराबर है यदि यह न्यूनतम केवल एक के लिए पहुँचता है i. अभीतक के लिए तो की मूल है P, न्यूनतम तक कम से कम दो बार पहुंचना चाहिए। अर्थात् दो मान होने चाहिए और का i ऐसा है कि और हरएक के लिए i.
वह है, और न्यूटन बहुभुज के एक किनारे से संबंधित होना चाहिए, और
संक्षेप में, एक मूल का मूल्यांकन P न्यूटन बहुपद के एक किनारे के ढलान के विपरीत होना चाहिए।
पुइसेक्स श्रृंखला विलयन का प्रारंभिक गुणांक आसानी से अनुमान लगाया जा सकता है. होने देना का प्रारंभिक गुणांक हो यानी का गुणांक में होने देना न्यूटन बहुभुज का ढलान हो, और संबंधित पुइसेक्स श्रृंखला विलयन का प्रारंभिक पद हो यदि कोई रद्दीकरण नहीं होगा, तो प्रारंभिक गुणांक होगा कहाँ I सूचकांकों का सेट है i ऐसा है कि ढलान के किनारे से संबंधित है न्यूटन बहुभुज का. तो, एक मूल होने के लिए, प्रारंभिक गुणांक बहुपद का एक शून्येतर मूल होना चाहिए
न्यूटन-पुइसेक्स प्रमेय के प्रमाण में पुइसेक्स श्रृंखला विलयनों के अगले शब्दों की पुनरावर्ती गणना के लिए इन प्रारंभिक शब्दों से प्रारंभ करना सम्मलित होगा।
रचनात्मक प्रमाण
मान लीजिए कि पहला पद पुइसेक्स श्रृंखला विलयन का पूर्ववर्ती अनुभाग की विधि द्वारा गणना की गई है। अभी हिसाब लगाना बाकी है इसके लिए हम सेट करते हैं और टेलर का विस्तार लिखें P पर
यह एक बहुपद है z जिनके गुणांक पुइसेक्स श्रृंखला में हैं x कोई इस पर न्यूटन बहुभुज की विधि लागू कर सकता है, और एक के बाद एक पुइसेक्स श्रृंखला की शर्तों को प्राप्त करने के लिए पुनरावृत्त कर सकता है। किन्तु उसका बीमा कराने के लिए कुछ सावधानी बरतनी पड़ती है और यह दिखाते हुए कि किसी को पुइसेक्स श्रृंखला मिलती है, अर्थात, के घातांक के प्रत्येक x बंधे रहन
के संबंध में व्युत्पत्ति y में मूल्यांकन नहीं बदलता है x गुणांकों का; वह है,
और समानता तब होती है जब और केवल यदि कहाँ पूर्ववर्ती अनुभाग का बहुपद है. यदि m की बहुलता है की मूल के रूप में इसका परिणाम यह होता है कि असमानता ही समानता है शर्तें ऐसी कि जहां तक मूल्यांकन का सवाल है, भुलाया जा सकता है और मतलब
इसका मतलब यह है कि, न्यूटन बहुभुज की विधि को दोहराने के लिए, किसी को न्यूटन बहुभुज के केवल उस भाग पर विचार करना चाहिए जिसका पहला निर्देशांक अंतराल से संबंधित है दो स्थितियों पर अलग से विचार करना होगा और वे अगले उपधाराओं का विषय होंगे, तथाकथित जटिल स्थितियों, जहां m > 1, और नियमित स्थितियों जहां m = 1
नियमित स्थिति
रामिफाइड स्थिति
न्यूटन बहुभुज की विधि को पुनरावर्ती रूप से लागू करने का तरीका पहले वर्णित किया गया है। जैसा कि विधि के प्रत्येक अनुप्रयोग में वृद्धि हो सकती है, रामिफाइड स्थिति में, घातांक (मूल्यांकन) के हर, यह प्रमाणित करना बाकी है कि एक सीमित संख्या में पुनरावृत्तियों के बाद नियमित स्थिति तक पहुंचता है (अन्यथा परिणामी श्रृंखला के घातांक के हर होंगे) बाध्य नहीं होगा, और यह श्रृंखला पुइसेक्स श्रृंखला नहीं होगी। वैसे, यह भी प्रमाणित हो जाएगा कि किसी को उतने ही पुइसेक्स श्रृंखला विलयन मिलते हैं जितनी अपेक्षा की जाती है, यही की डिग्री है में y
व्यापकता की हानि के बिना, कोई ऐसा मान सकता है वह है, दरअसल, प्रत्येक कारक y का एक विलयन प्रदान करता है जो शून्य पुइसेक्स श्रृंखला है, और ऐसे कारकों को दूर किया जा सकता है।
जैसे विशेषता शून्य मानी जाती है, वैसा भी कोई मान सकता है एक वर्ग-मुक्त बहुपद है, अर्थात इसका विलयन है सभी अलग हैं. दरअसल, वर्ग-मुक्त गुणनखंडन गुणनखंडन के लिए केवल गुणांक के क्षेत्र के संचालन का उपयोग करता है वर्ग-मुक्त कारकों में अलग से हल किया जा सकता है। (विशेषता शून्य की परिकल्पना की आवश्यकता है, क्योंकि, विशेषता में p, वर्ग-मुक्त अपघटन अघुलनशील कारक प्रदान कर सकता है, जैसे जिसके बीजगणितीय विस्तार पर अनेक मूल होंते है।)
इस संदर्भ में, कोई न्यूटन बहुभुज के किनारे की लंबाई को उसके अंतिम बिंदुओं के भुज के अंतर के रूप में परिभाषित करता है। बहुभुज की लंबाई उसके किनारों की लंबाई का योग होती है। परिकल्पना के साथ न्यूटन बहुभुज की लंबाई P इसकी डिग्री है y, वह इसकी मूलों की संख्या है। न्यूटन बहुभुज के एक किनारे की लंबाई किसी दिए गए मूल्यांकन की मूलों की संख्या है। यह संख्या पहले से परिभाषित बहुपद की घात के बराबर है
इस प्रकार, व्यापक स्थितियों दो (या अधिक) विलयनों से मेल खाता है जिनके प्रारंभिक शब्द समान हैं। चूंकि ये विलयन अलग-अलग होने चाहिए (वर्ग-मुक्त परिकल्पना), उन्हें पुनरावृत्तियों की एक सीमित संख्या के बाद अलग किया जाना चाहिए। अर्थात्, अंततः एक बहुपद प्राप्त होता है यह वर्ग मुक्त है, और गणना प्रत्येक मूल के लिए नियमित स्थिति की तरह जारी रह सकती है चूंकि नियमित स्थिति की पुनरावृत्ति घातांक के हरों में वृद्धि नहीं करती है, इससे पता चलता है कि विधि सभी विलयनों को पुइसेक्स श्रृंखला के रूप में प्रदान करती है, अर्थात, जटिल संख्याओं पर पुइसेक्स श्रृंखला का क्षेत्र एक बीजगणितीय रूप से बंद क्षेत्र है जिसमें अविभाज्य बहुपद सम्मलित जटिल गुणांक के साथ होती हैं।
सकारात्मक विशेषता में विफलता
न्यूटन-पुइसेक्स प्रमेय सकारात्मक विशेषता वाले क्षेत्रों पर मान्य नहीं है। उदाहरण के लिए, समीकरण विलयन है
और
(कोई पहले कुछ पदों पर आसानी से जांच कर सकता है कि इन दोनों श्रृंखलाओं का योग और उत्पाद 1 और है क्रमश; यह तब मान्य होता है जब आधार क्षेत्र K की विशेषता 2 से भिन्न होती है)।
चूँकि पिछले उदाहरण के गुणांकों के हर में 2 की घातें किसी को विश्वास दिला सकती हैं, प्रमेय का कथन सकारात्मक विशेषता में सत्य नहीं है। आर्टिन-श्रेयर प्रमाणित ांत का उदाहरण आर्टिन-श्रेयर समीकरण यह दिखाता है: मूल्यांकन के साथ तर्क से पता चलता है कि एक्स का मूल्यांकन होना चाहिए , और यदि हम इसे इस रूप में पुनः लिखते हैं तब
और एक वैसा ही दिखाता है मूल्यांकन होना चाहिए , और उस विधि से आगे बढ़ने पर व्यक्ति श्रृंखला प्राप्त करता है
चूंकि इस श्रृंखला का पुइसेक्स श्रृंखला के रूप में कोई मतलब नहीं है - क्योंकि घातांक में असीमित हर हैं - मूल समीकरण का कोई विलयन नहीं है। चूँकि , ऐसे आइज़ेंस्टीन के मानदंड अनिवार्य रूप से एकमात्र विलयन नहीं हैं, क्योंकि, यदि बीजगणितीय रूप से विशेषता से बंद है , फिर पुइसेक्स श्रृंखला का क्षेत्र खत्म के अधिकतम वश में रामीकरण (गणित) विस्तार का पूर्ण समापन है [4]
इसी प्रकार बीजगणितीय समापन के स्थिति में, वास्तविक बंद क्षेत्र के लिए एक अनुरूप प्रमेय है: यदि एक वास्तविक बंद क्षेत्र है, फिर पुइसेक्स श्रृंखला का क्षेत्र खत्म हो गया यह औपचारिक लॉरेंट श्रृंखला के क्षेत्र का वास्तविक समापन होता है [5] (यह पूर्व प्रमेय का तात्पर्य है क्योंकि विशेषता शून्य का कोई भी बीजगणितीय रूप से बंद क्षेत्र कुछ वास्तविक-बंद क्षेत्र का अद्वितीय द्विघात विस्तार है।)
पी-एडिकली बंद क्षेत्र|पी-एडिक क्लोजर: यदि के लिए भी एक समान परिणाम है एक है -मूल्यांकन के संबंध में मौलिक रूप से बंद क्षेत्र , फिर पुइसेक्स श्रृंखला का क्षेत्र खत्म ई आल्सो -वैधिक रूप से बंद होता है। [6]
बीजगणितीय वक्रों और फलनों का पुइसेक्स विस्तार
बीजगणितीय वक्र
मान लीजिए एक बीजगणितीय वक्र है[7] जो एक एफ़िन समीकरण द्वारा दिया गया है बीजगणितीय रूप से बंद क्षेत्र पर विशेषता शून्य का, और एक बिंदु पर विचार करें पर जिसे हम मान सकते हैं हम भी यही मानते हैं की निर्देशांक अक्ष नहीं होता है फिर (द.) का पुइसेक्स विस्तार का समन्वय) पर एक पुइसेक्स श्रृंखला है का सकारात्मक मूल्यांकन होता है।
अधिक त्रुटिहीन रूप से, आइए हम इसकी ब्रांच को परिभाषित करें पर अंक होना नोएथेर सामान्यीकरण लेम्मा का का कौन सा मानचित्र बनाना है . ऐसे प्रत्येक के लिए , एक स्थानीय समन्वय है का पर (जो एक सहज बिंदु है) जैसे कि निर्देशांक और की औपचारिक घात श्रेणी के रूप में व्यक्त किया जा सकता है , कहना (तब से बीजगणितीय रूप से बंद है, हम मूल्यांकन गुणांक 1) और मान सकते हैं : फिर फॉर्म की एक अनूठी पुइसेक्स श्रृंखला है (एक घात श्रेणी में ), ऐसा है कि (बाद वाली अभिव्यक्ति तब से सार्थक है में एक सुपरिभाषित घात श्रेणी है ). यह पुइसेक्स का विस्तार है पर जो कि दी गई शाखा से जुड़ा बताया जा रहा है (या बस, उस शाखा का पुइसेक्स विस्तार ), और प्रत्येक पुइसेक्स विस्तार पर की एक अनूठी शाखा के लिए इस प्रकार दिया गया है पर .[8][9] बीजगणितीय वक्र या फ़ंक्शन की ब्रांच के औपचारिक पैरामीट्रिजेशन के इस अस्तित्व को पुइसेक्स के प्रमेय के रूप में भी जाना जाता है: इसमें तर्कसंगत रूप से वही गणितीय सामग्री है जो तथ्य यह है कि पुइसेक्स श्रृंखला का क्षेत्र बीजगणितीय रूप से बंद है और ऐतिहासिक रूप से अधिक त्रुटिहीन विवरण है मूल लेखक का कथन है [10]
उदाहरण के लिए, वक्र (जिसका सामान्यीकरण समन्वय के साथ एक रेखा है और मानचित्र ) की दोहरे बिंदु (0,0) पर दो शाखाएँ हैं, जो बिंदुओं के अनुरूप हैं और सामान्यीकरण पर, जिसका पुइसेक्स विस्तार है और क्रमशः (यहाँ, दोनों घात श्रेणी हैं क्योंकि सामान्यीकरण में संगत बिंदुओं पर निर्देशांक एटेले मॉर्फिज्म होते है)। बिंदु पर (जो है सामान्यीकरण में), इसकी एक ही उपखंड होता है, जो पुइसेक्स विस्तार द्वारा दी गई है (द निर्देशांक इस बिंदु पर प्रभाव डालता है, इसलिए यह एक घात श्रृंखला नहीं है)।
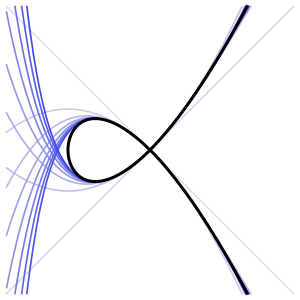
वक्र (जिसका सामान्यीकरण फिर से निर्देशांक के साथ एक रेखा है और मानचित्र ), दूसरी ओर, नोक (विलक्षणता) पर एक ही श्रेणी होती है , जिसका पुइसेक्स विस्तार होता है।
विश्लेषणात्मक अभिसरण
जब सम्मिश्र संख्याओं का क्षेत्र होता है, एक बीजगणितीय वक्र का पुइसेक्स विस्तार (जैसा कि ऊपर परिभाषित किया गया है) इस अर्थ में अभिसरण है कि दिए गए विकल्प के लिए -वें की मूल , वे अधिक छोटे से अभिसरण करते हैं इसलिए प्रत्येक शाखा का एक विश्लेषणात्मक पैरामीटरीकरण परिभाषित करें के निकटतम में (अधिक त्रुटिहीन रूप से, पैरामीट्रिज़ेशन इसके -वें की मूल द्वारा होता है)।
सामान्यीकरण
लेवी-सिविटा क्षेत्र
पुइसेक्स श्रृंखला का क्षेत्र मीट्रिक स्थान के रूप में पूर्ण नहीं है। इसका समापन, जिसे लेवी-सिविटा क्षेत्र कहा जाता है, को इस प्रकार वर्णित किया जा सकता है: यह विधि औपचारिक अभिव्यक्ति का क्षेत्र होता है जहां गुणांकों का समर्थन (अर्थात्, e का समुच्चय ऐसा है कि ) परिमेय संख्याओं के बढ़ते अनुक्रम की सीमा है जो या तो परिमित है या इसकी ओर प्रवृत्त होता है दूसरे शब्दों में, ऐसी शृंखलाएं असीमित हरों के घातांकों को स्वीकार करती हैं, परंतु कि इससे से कम घातांक के परिमित रूप से अनेक पद किसी दिए गए बंधन के लिए उदाहरण के लिए, पुइसेक्स श्रृंखला नहीं होते है, किन्तु यह पुइसेक्स श्रृंखला के कॉची अनुक्रम की शृंखला होती है; विशेष रूप से, यह सीमा जैसा होती है चूँकि , यह पूर्णता अभी भी इस अर्थ में अधिकतम रूप से पूर्ण नहीं है कि यह गैर-तुच्छ विस्तारों को स्वीकार करती है जो समान मूल्य समूह और अवशेष क्षेत्र वाले मूल्यवान क्षेत्र होते हैं,[11][12] इसलिए इसे पूरा करने का अवसर और भी अधिक होता है।
हैन श्रृंखला
हैन श्रृंखला पुइसेक्स श्रृंखला का एक और (बड़ा) सामान्यीकरण है, जिसे हंस हैन (गणितज्ञ) ने 1907 में अपने हैन एम्बेडिंग प्रमेय के प्रमाण के समय प्रस्तुत किया था और फिर हिल्बर्ट की सत्रहवीं समस्या के दृष्टिकोण में उनके द्वारा अध्ययन किया गया था। हैन श्रृंखला में, घातांकों को परिबद्ध हर की आवश्यकता के अधिकांशतः उन्हें मूल्य समूह (सामान्यतः) का सुव्यवस्थित उपसमुच्चय बनाने की आवश्यकता होती है (सामान्यतः या ) इन्हें बाद में अनातोली माल्टसेव और बर्नहार्ड न्यूमैन द्वारा एक गैर-कम्यूटेटिव सेटिंग में सामान्यीकृत किया गया (इसलिए उन्हें कभी-कभी हैन-मालसेव-न्यूमैन श्रृंखला के रूप में जाना जाता है)। हैन श्रृंखला का उपयोग करते हुए, सकारात्मक विशेषता में शक्ति श्रृंखला के क्षेत्र के बीजगणितीय समापन का विवरण देना संभव है जो कुछ हद तक पुइसेक्स श्रृंखला के क्षेत्र के अनुरूप है।[13]
टिप्पणियाँ
- ↑ Newton (1960)
- ↑ 2.0 2.1 Puiseux (1850, 1851)
- ↑ Newton (1736)
- ↑ 4.0 4.1 cf. Kedlaya (2001), introduction
- ↑ Basu &al (2006), chapter 2 ("Real Closed Fields"), theorem 2.91 (p. 75)
- ↑ Cherlin (1976), chapter 2 ("The Ax–Kochen–Ershof Transfer Principle"), §7 ("Puiseux series fields")
- ↑ We assume that is irreducible or, at least, that it is reduced and that it does not contain the coordinate axis.
- ↑ Shafarevich (1994), II.5, pp. 133–135
- ↑ Cutkosky (2004), chapter 2, pp. 3–11
- ↑ Puiseux (1850), p. 397
- ↑ Poonen, Bjorn (1993). "अधिकतम पूर्ण फ़ील्ड". Enseign. Math. 39: 87–106.
- ↑ Kaplansky, Irving (1942). "मूल्यांकन के साथ अधिकतम फ़ील्ड". Duke Math. J. 9 (2): 303–321. doi:10.1215/s0012-7094-42-00922-0.
- ↑ Kedlaya (2001)
यह भी देखें
- लॉरेंट श्रृंखला
- माधव श्रृंखला
- न्यूटन बहुपद|न्यूटन का विभाजित अंतर प्रक्षेप
- पाडे सन्निकटन
संदर्भ
- Basu, Saugata; Pollack, Richard; Roy, Marie-Françoise (2006). Algorithms in Real Algebraic Geometry. Algorithms and Computations in Mathematics 10 (2nd ed.). Springer-Verlag. doi:10.1007/3-540-33099-2. ISBN 978-3-540-33098-1.
- Cherlin, Greg (1976). Model Theoretic Algebra Selected Topics. Lecture Notes in Mathematics 521. Springer-Verlag. ISBN 978-3-540-07696-4.[dead link]
- Cutkosky, Steven Dale (2004). Resolution of Singularities. Graduate Studies in Mathematics 63. American Mathematical Society. ISBN 0-8218-3555-6.
- Eisenbud, David (1995). Commutative Algebra with a View Toward Algebraic Geometry. Graduate Texts in Mathematics 150. Springer-Verlag. ISBN 3-540-94269-6.
- Kedlaya, Kiran Sridhara (2001). "The algebraic closure of the power series field in positive characteristic". Proc. Amer. Math. Soc. 129 (12): 3461–3470. doi:10.1090/S0002-9939-01-06001-4.
- Newton, Isaac (1736) [1671], The method of fluxions and infinite series; with its application to the geometry of curve-lines, translated by Colson, John, London: Henry Woodfall, p. 378 (Translated from Latin)
- Newton, Isaac (1960). "letter to Oldenburg dated 1676 Oct 24". The correspondence of Isaac Newton. Vol. II. Cambridge University press. pp. 126–127. ISBN 0-521-08722-8.
- Puiseux, Victor Alexandre (1850). "Recherches sur les fonctions algébriques" (PDF). J. Math. Pures Appl. 15: 365–480.
- Puiseux, Victor Alexandre (1851). "Nouvelles recherches sur les fonctions algébriques" (PDF). J. Math. Pures Appl. 16: 228–240.
- Shafarevich, Igor Rostislavovich (1994). Basic Algebraic Geometry (2nd ed.). Springer-Verlag. ISBN 3-540-54812-2.
- Walker, R.J. (1978). Algebraic Curves (PDF) (Reprint ed.). Springer-Verlag. ISBN 0-387-90361-5.