समूह विलंब और चरण विलंब

संकेत संसाधन में, समूह विलंब और चरण विलंब संकेत के विभिन्न आवृति घटकों द्वारा अनुभव किए जाने वाले विलंब समय मे होते हैं, जब संकेत एक ऐसी प्रणाली से गुजरता है जो रैखिक समय-अपरिवर्तनीय है, जैसे कि माइक्रोफ़ोन, समाक्षीय केबल, प्रवर्धक, लाउडस्पीकर, दूरसंचार सिस्टम या ईथरनेट केबल। ये विलंब सामान्यतः आवृत्ति पर निर्भर होते है। इसका मतलब है कि विभिन्न आवृत्ति घटक अलग-अलग विलंब का अनुभव करते हैं, जो संकेत के तरंग के विरूपण का कारण बनते हैं क्योंकि यह सिस्टम से गुजरता है। यह विकृति एनालॉग वीडियो और एनालॉग ऑडियो में खराब उच्च विश्वस्तता या उपकरण बिट वर्ग में उच्च बिट-त्रुटि दर जैसी समस्याएं उत्पन्न कर सकती है। मॉड्यूलेशन संकेत के लिए, संकेत बुद्धिमत्ता को विशेष रूप से तरंग एनवेलप कर में ले जाया जाता है। समूह विलंब केवल एनवेलप से प्राप्त आवृत्ति घटकों के साथ संचालित होता है।

परिचय

रैखिक समय-अपरिवर्तनीय प्रणाली के समूह विलंब और चरण विलंब गुण आवृत्ति के कार्य हैं, जो उस समय देते हैं जब किसी समय के संकेत के आवृत्ति घटक भौतिक मात्रा में भिन्न होते हैं-उदाहरण के लिए वोल्टेज संकेत- एलटीआई सिस्टम इनपुट पर उस समय दिखाई देता है जब उसी आवृत्ति घटक की एक प्रति पर प्रकट होता है -एक अलग भौतिक घटना-एलटीआई सिस्टम आउटपुट पर दिखाई देता है।

आवृत्ति के एक कार्य के रूप में एक भिन्न चरण प्रतिक्रिया, जिससे समूह विलंब और चरण विलंब की गणना की जा सकती है, सामान्यतः इक्रोफ़ोन, प्रवर्धक, लाउडस्पीकर, चुंबकीय रिकॉर्डर, हेडफ़ोन, समाक्षीय केबल और एंटीएलियासिंग फ़िल्टर जैसे उपकरणों में होती है। संकेत के सभी आवृत्ति घटकों में विलंब हो जाती है जब ऐसे उपकरणों के माध्यम से पारित किया जाता है, या जब अंतरिक्ष या माध्यम से फैलता है, जैसे हवा या पानी।

चरण विलंब

एक रैखिक समय-अपरिवर्तनीय प्रणाली या उपकरण में एक चरण प्रतिक्रिया सामग्री और एक चरण विलंब सामग्री होती है, जहां एक की गणना दूसरे से की जा सकती है। चरण विलंब सीधे व्यक्तिगत आवृत्ति घटकों के उपकरण या सिस्टम समय विलंब को मापता है। यदि किसी निश्चित आवृत्ति पर चरण विलंब कार्य-ब्याज की आवृत्ति सीमा के भीतर - चयनित आवृत्ति पर चरण और स्वयं चयनित आवृत्ति के बीच आनुपातिकता का समान स्थिरांक होता है, तो सिस्टम/ उपकरण में एक फ्लैट चरण विलंब सामग्री का आदर्श, a.k.a. रैखिक चरण होते है । चूंकि चरण विलंब समय की विलंब देने वाली आवृत्ति का एक कार्य है, इसके फ़ंक्शन ग्राफ़ की समतलता से एक प्रस्थान विभिन्न संकेत के आवृति घटकों के बीच समय की विलंब के अंतर को प्रकट कर सकता है, जिस स्थिति में वे अंतर संकेत विरूपण में योगदान करेंगे, जो कि आउटपुट संकेत वेवफॉर्म शेप के रूप में प्रकट होता है जो इनपुट संकेत से अलग होता है। यदि उपकरण इनपुट एक मॉड्यूलेशन संकेत है, तो चरण विलंब सामग्री सामान्य रूप से उपयोगी जानकारी नहीं देती है। उसके लिए समूह विलंब का उपयोग करना चाहिए।

समूह विलंब

चित्र 1: बाहरी और आंतरिक एलटीआई उपकरण

समूह विलंब एक मॉडुलन प्रणाली में आवृत्ति के संबंध में चरण की रैखिकता का एक सुविधाजनक उपाय है।

बुनियादी मॉडुलन प्रणाली

उपकरण के समूह विलंब की गणना उपकरण की चरण प्रतिक्रिया से की जा सकती है, लेकिन इसके विपरीत नहीं।

समूह विलंब के लिए सबसे सरल उपयोग मामला चित्र 1 में दिखाया गया है जो एक वैचारिक मॉडुलन प्रणाली को दर्शाता है, जो स्वयं एक बेसबैंड आउटपुट के साथ एक एलटीआई प्रणाली है जो आदर्श रूप से बेसबैंड संकेत इनपुट की एक सुनिश्चित प्रति है। समग्र रूप से इस प्रणाली को यहां बाहरी एलटीआई उपकरण के रूप में संदर्भित किया जाता है, जिसमें एक आंतरिक (लाल ब्लॉक) एलटीआई उपकरण होता है। जैसा कि अक्सर एक रेडियो सिस्टम के मामले में होता है, चित्र 1 में आंतरिक लाल एलटीआई सिस्टम कैस्केड में दो एलटीआई सिस्टम का प्रतिनिधित्व कर सकता है, उदाहरण के लिए एक प्रवर्धक भेजने वाले अंत में एक संचारण एंटीना और दूसरा एंटीना और प्रवर्धक प्राप्त करने के अंत में होता है।

आयाम मॉडुलन मापीय

विपुलता मॉड्यूलेशन बेसबैंड आवृति घटकों को बहुत अधिक आवृति रेंज में स्थानांतरित करके पासबैंड संकेत बनाता है। हालांकि आवृत्तियां अलग-अलग हैं, पासबैंड संकेत बेसबैंड संकेत के समान ही जानकारी रखता है। डेमोडुलेटर उलटा करता है, पासबैंड आवृत्तियों को मूल बेसबैंड आवृत्ति रेंज में वापस स्थानांतरित कर देता है। आदर्श रूप से, आउटपुट संकेत, इनपुट संकेत का एक समय विलंबित संस्करण है जहां आउटपुट का तरंग आकार इनपुट के समान होता है।

चित्र 1 में, बाहरी सिस्टम चरण विलंब सार्थक प्रदर्शन मापीय है। आयाम मॉडुलन के लिए, आंतरिक लाल एलटीआई उपकरण समूह विलंब बाहरी एलटीआई उपकरण चरण विलंब बन जाता है। यदि आंतरिक लाल उपकरण समूह विलंब ब्याज की आवृत्ति रेंज में पूरी तरह से चपटी होती है, तो बाहरी उपकरण में एक चरण विलंब का आदर्श होगा, जहां बाहरी एलटीआई उपकरण के चरण प्रतिक्रिया के कारण विरूपण का योगदान-पूरी तरह से निर्धारित होता है आंतरिक उपकरण की संभावित रूप से भिन्न चरण प्रतिक्रिया द्वारा-समाप्त हो जाती है। उस स्थिति में, आंतरिक लाल उपकरण की समूह विलंब और बाहरी उपकरण की चरण विलंब बेसबैंड इनपुट से बेसबैंड आउटपुट तक संकेत के लिए एक ही समय विलंब का आंकड़ा देती है। यह ध्यान रखना महत्वपूर्ण है कि आंतरिक लाल उपकरण के लिए बहुत गैर-फ्लैट चरण विलंब (लेकिन फ्लैट समूह विलंब) होना संभव है, जबकि बाहरी उपकरण में पूरी तरह से फ्लैट चरण विलंब का आदर्श होता है। यह सौभाग्य की बात है क्योंकि एलटीआई उपकरण डिजाइन में, फ्लैट चरण विलंब की तुलना में एक फ्लैट समूह विलंब प्राप्त करना आसान होता है।

कोण मॉडुलन

कोण -मॉड्यूलेशन सिस्टम में - जैसे आवृति मॉड्यूलेशन (एफएम) या फ़ेज़ मॉड्यूलेशन के साथ -एलटीआई सिस्टम इनपुट पर लागू (एफएम या पीएम) पासबैंड संकेत का विश्लेषण दो अलग-अलग पासबैंड संकेत के रूप में किया जा सकता है, एक इन-फ़ेज़ ( I) आयाम मॉडुलन पासबैंड संकेत और एक चतुर्भुज-चरण (क्यू) आयाम मॉड्यूलेशन पासबैंड संकेत, जहां उनका योग वास्तव में मूल कोण-मॉड्यूलेशन (एफएम या पीएम) पासबैंड संकेत का पुनर्निर्माण करता है। जबकि (एफएम/पीएम) पासबैंड संकेत आयाम मॉडुलन नहीं है, और इसलिए कोई स्पष्ट बाहरी लिफाफा नहीं है, आई और क्यू पासबैंड संकेत में वास्तव में आयाम मॉड्यूलेशन एनवेलप हैं। (हालांकि, नियमित आयाम मॉडुलन के विपरीत, I और क्यू बेसबैंड संकेत के तरंग आकार के समान नहीं होते हैं, भले ही बेसबैंड संकेत का 100 प्रतिशत उनके एनवेलप द्वारा जटिल तरीके से दर्शाया जाता है।) इसलिए, प्रत्येक के लिए I और क्यू पासबैंड संकेत, एक फ्लैट समूह विलंब सुनिश्चित करता है कि न तो I पास बैंड लिफाफा और न ही क्यू पासबैंड एनवेलप में तरंग आकार विकृति होगी, इसलिए जब I पासबैंड संकेत और क्यू पासबैंड संकेत को एक साथ वापस जोड़ा जाता है, तो योग मूल है एफएम/पीएम पासबैंड संकेत, जिसे भी बदला नहीं जाएगा।

पृष्ठभूमि

एक आवधिक संकेत के लिए, एक आवृत्ति घटक गुणों के साथ एक साइन वक्र होता है जिसमें समय-आधारित आवृत्ति और चरण शामिल होते हैं।

एक मूल साइन वक्र उत्पन्न करना

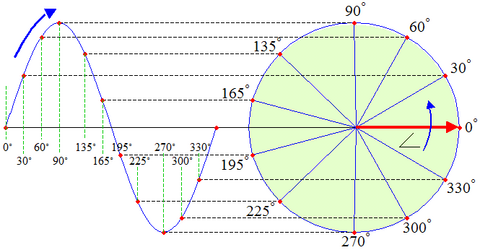
साइन वक्र, समय आधारित आवृत्ति सामग्री के साथ या बिना, एक सर्कल द्वारा उत्पन्न होता है जैसा कि चित्र में दिखाया गया है। इस उदाहरण में, साइन वक्र एक साइन वेव है जिसे का उपयोग करके पता लगाया जाता है $\sin$ त्रिकोणमितीय समारोह।

सदिश का अनुरेखण घूर्णन करते हुए $\sin()$ समारोह। चरण 1 प्ले दबाएं। चरण 2 अधिकतम चरण 3 वेबएम स्रोत चुनें

जब एक बढ़ता हुआ कोण $x$ सर्कल के चारों ओर एक पूर्ण सीसीडब्ल्यू रोटेशन बनाता है, फ़ंक्शन के पैटर्न का एक चक्र उत्पन्न होता है। 360 डिग्री से आगे के कोण को और बढ़ाना बस फिर से सर्कल के चारों ओर घूमता है, एक और चक्र पूरा करता है, जहां प्रत्येक सफल चक्र एक ही पैटर्न को दोहराता है, जिससे फ़ंक्शन आवधिक हो जाता है। (देखें सदिश घूर्णन... एनीमेशन बाईं ओर।) कोण मान की कोई सीमा नहीं होती है, और इसलिए पैटर्न जितनी बार स्वयं को दोहराता है उसकी भी कोई सीमा नहीं होती है। इस वजह से, साइन वक्र की कोई शुरुआत नहीं है और कोई अंत नहीं है। एक साइन वक्रल फ़ंक्शन त्रिकोणमितीय कार्यों में से किसी एक या दोनों पर आधारित होता है $\sin(x)$ तथा $\cos(x)$.

सिद्धांत

एलटीआई प्रणाली सिद्धांत में, नियंत्रण सिद्धांत, और डिजिटल संकेत प्रोसेसिंग या एनालॉग संकेत प्रोसेसिंग में, इनपुट संकेत के बीच संबंध, $\displaystyle x(t)$ और आउटपुट संकेत, $\displaystyle y(t)$, एक LTI प्रणाली एक कनवल्शन ऑपरेशन द्वारा शासित होती है:

$y(t)=(h*x)(t)\ {\stackrel {\mathrm {def} }{=}}\ \int _{-\infty }^{\infty }x(u)h(t-u)\,du$

या, आवृत्ति डोमेन में,

$Y(s)=H(s)X(s)\,$

कहाँ पे

$X(s)={\mathcal {L}}{\Big \{}x(t){\Big \}}\ {\stackrel {\mathrm {def} }{=}}\ \int _{-\infty }^{\infty }x(t)e^{-st}\,dt$

$Y(s)={\mathcal {L}}{\Big \{}y(t){\Big \}}\ {\stackrel {\mathrm {def} }{=}}\ \int _{-\infty }^{\infty }y(t)e^{-st}\,dt$

तथा

$H(s)={\mathcal {L}}{\Big \{}h(t){\Big \}}\ {\stackrel {\mathrm {def} }{=}}\ \int _{-\infty }^{\infty }h(t)e^{-st}\,dt$.

यहां $\displaystyle h(t)$ एलटीआई प्रणाली की समय-क्षेत्रीय आवेग प्रतिक्रिया है और $\displaystyle X(s)$, $\displaystyle Y(s)$, $\displaystyle H(s)$, इनपुट के लाप्लास रूपांतर हैं $\displaystyle x(t)$, आउटपुट $\displaystyle y(t)$, और आवेग प्रतिक्रिया $\displaystyle h(t)$, क्रमश। $\displaystyle H(s)$ एलटीआई प्रणाली का स्थानांतरण कार्य कहा जाता है और, आवेग प्रतिक्रिया की तरह $\displaystyle h(t)$, एलटीआई प्रणाली की इनपुट-आउटपुट विशेषताओं को पूरी तरह से परिभाषित करता है।

मान लीजिए कि ऐसी प्रणाली एक अर्ध-साइन वक्रल संकेत द्वारा संचालित होती है, जैसे कि एक साइन लहर जिसमें एक आयाम लिफाफा होता है $\displaystyle a(t)>0$ जो आवृत्ति के सापेक्ष धीरे-धीरे बदल रहा है $\displaystyle \omega$ साइन वक्र का। गणितीय रूप से, इसका मतलब है कि अर्ध-साइन वक्रल ड्राइविंग संकेत का रूप है

$x(t)=a(t)\cos(\omega t+\theta )\$

और धीरे-धीरे बदलते आयाम लिफाफा $\displaystyle a(t)$ मतलब कि

$\left|{\frac {d}{dt}}\log {\big (}a(t){\big )}\right|\ll \omega \ .$

तब इस तरह के एक एलटीआई सिस्टम का आउटपुट बहुत अच्छी तरह से अनुमानित है

$y(t)={\big |}H(i\omega ){\big |}\ a(t-\tau _{g})\cos {\big (}\omega (t-\tau _{\phi })+\theta {\big )}\;.$

यहां $\displaystyle \tau _{g}$ समूह विलंब है और $\displaystyle \tau _{\phi }$ चरण विलंब है, और वे नीचे दिए गए भावों द्वारा दिए गए हैं (और संभावित रूप से कोणीय आवृत्ति के कार्य हैं $\displaystyle \omega$) साइन वक्र का चरण, जैसा कि शून्य क्रॉसिंग की स्थिति से संकेत मिलता है, चरण विलंब के बराबर राशि से समय में विलंब होती है, $\displaystyle \tau _{\phi }$. समूह की विलंब से साइन वक्र का लिफाफा समय पर विलंबित होता है, $\displaystyle \tau _{g}$.

एक रैखिक चरण प्रणाली में (नॉन-इनवर्टिंग गेन के साथ), दोनों $\displaystyle \tau _{g}$ तथा $\displaystyle \tau _{\phi }$ स्थिर हैं (अर्थात, से स्वतंत्र) $\displaystyle \omega$) और बराबर, और उनका सामान्य मूल्य सिस्टम के समग्र विलंब के बराबर होता है; और सिस्टम के अलिखित चरण (लहरें) (अर्थात् $\displaystyle -\omega \tau _{\phi }$) ऋणात्मक है, परिमाण आवृत्ति के साथ रैखिक रूप से बढ़ रहा है $\displaystyle \omega$.

अधिक सामान्यतः, यह दिखाया जा सकता है कि स्थानांतरण फ़ंक्शन वाले एलटीआई सिस्टम के लिए $\displaystyle H(s)$ इकाई आयाम के एक चरण द्वारा संचालित,

$x(t)=e^{i\omega t}\$

आउटपुट है

${\begin{aligned}y(t)&=H(i\omega )\ e^{i\omega t}\ \\&=\left({\big |}H(i\omega ){\big |}e^{i\phi (\omega )}\right)\ e^{i\omega t}\ \\&={\big |}H(i\omega ){\big |}\ e^{i\left(\omega t+\phi (\omega )\right)}\ \\\end{aligned}}\$

जहां चरण बदलाव $\displaystyle \phi$ है

$\phi (\omega )\ {\stackrel {\mathrm {def} }{=}}\ \arg \left\{H(i\omega )\right\}\;.$

इसके अतिरिक्त, यह दिखाया जा सकता है कि समूह विलंबित है, $\displaystyle \tau _{g}$, और चरण विलंब, $\displaystyle \tau _{\phi }$, आवृत्ति-निर्भर हैं।उनकी गणना फेज अनरैपिंग फेज शिफ्ट से की जा सकती है $\displaystyle \phi$ द्वारा

$\tau _{g}(\omega )=-{\frac {d\phi (\omega )}{d\omega }}\$

$\tau _{\phi }(\omega )=-{\frac {\phi (\omega )}{\omega }}\$ .

अर्थात्, प्रत्येक आवृत्ति पर समूह विलंब चरण के ढलान के ऋणात्मक के बराबर होता है वह आवृत्ति(तात्कालिक आवृत्ति की तुलना)।

नकारात्मक समूह विलंब वाले सर्किट संभव हैं, हालांकि कार्य-कारण का उल्लंघन नहीं किया गया है।

ऑडियो में समूह विलंब

ऑडियो क्षेत्र में और विशेष रूप से ध्वनि प्रजनन क्षेत्र में समूह विलंब का कुछ महत्व है।एक ऑडियो प्रजनन श्रृंखला के कई घटक, विशेष रूप से लाउडस्पीकर और मल्टीवे लाउडस्पीकर ऑडियो क्रॉसओवर, ऑडियो संकेत में समूह विलंब का परिचय देते हैं।इसलिए आवृत्ति के संबंध में समूह विलंब की श्रव्यता की सीमा जानना महत्वपूर्ण है,विशेष रूप से यदि ऑडियो श्रृंखला उच्च विश्वस्तता प्रजनन प्रदान करने वाली हो। श्रव्यता तालिका की सर्वोत्तम सीमाएँ Blauert and Laws द्वारा प्रदान की गई हैं।

Frequency (kHz)	Threshold (ms)	Periods (Cycles)
0.5	3.2	1.6
1	2	2
2	1	2
4	1.5	6
8	2	16

फ्लैनगन, मूर और स्टोन ने निष्कर्ष निकाला है कि 1, 2 और 4 kHz पर, गैर-प्रतिवर्ती स्थिति में हेडफ़ोन के साथ लगभग 1.6 ms का समूह विलंब श्रव्य है।अन्य प्रयोगात्मक परिणाम बताते हैं कि जब समूह की आवृत्ति रेंज में 300 हर्ट्ज से 1 किलोहर्ट्ज़ तक की विलंब 1.0 एमएस से कम है, तो यह अश्रव्य है।

एक ऑडियो संकेत के तरंग को एक सिस्टम द्वारा ठीक से पुन: पेश किया जा सकता है जिसमें संकेत की बैंडविड्थ पर एक फ्लैट आवृत्ति प्रतिक्रिया होती है और एक चरण विलंब जो समूह विलंब के बराबर होता है। नमकीन पानीविभेदक समय-विलंब विकृति की अवधारणा को पेश किया, जिसे चरण विलंब और समूह विलंब के बीच अंतर के रूप में परिभाषित किया गया है, जो इसके द्वारा दिया गया है:

$\Delta \tau =\tau _{\phi }-\tau _{g}$.

एक आदर्श प्रणाली को शून्य या नगण्य अंतर समय-विलंब विरूपण प्रदर्शित करना चाहिए।

मल्टी-वे लाउडस्पीकर सिस्टम में क्रॉसओवर नेटवर्क के उपयोग के कारण उत्पन्न होने वाले समूह विलंब विकृति को ठीक करने के लिए डिजिटल संकेत प्रोसेसिंग तकनीकों का उपयोग करना संभव है।इसमें विलंब समीकरण को सफलतापूर्वक लागू करने के लिए लाउडस्पीकर सिस्टम का काफी कम्प्यूटेशनल मॉडलिंग शामिल है,पार्क्स-मैकलेलन फ़िल्टर डिज़ाइन एल्गोरिथम का उपयोग करना | पार्क्स-मैकलेलन एफआईआर इक्विरिपल फ़िल्टर डिज़ाइन एल्गोरिथम।

प्रकाशिकी में समूह विलंब

भौतिकी में और विशेष रूप से प्रकाशिकी में समूह विलंब महत्वपूर्ण है।

एक ऑप्टिकल फाइबर में, समूह विलंब ऑप्टिकल पावर ) के लिए आवश्यक पारगमन समय है, जो किसी दिए गए दूरी की यात्रा करने के लिए किसी दिए गए ट्रांसवर्स मोड के समूह वेग पर यात्रा करता है। ऑप्टिकल फाइबर फैलाव (प्रकाशिकी) माप उद्देश्यों के लिए, ब्याज की मात्रा समूह प्रसार विलंब प्रति इकाई लंबाई है, जो एक विशेष मोड के समूह वेग का पारस्परिक है। एक ऑप्टिकल फाइबर के माध्यम से एक संकेतिंग दूरसंचार के मापा समूह विलंब फाइबर में मौजूद विभिन्न फैलाव प्रकाशिकी तंत्र के कारण तरंग दैर्ध्य निर्भरता प्रदर्शित करता है।

समूह विलंब के लिए सभी आवृत्तियों पर स्थिर होना अक्सर वांछनीय होता है; अन्यथा संकेत का अस्थायी धुंधलापन होता है। क्योंकि समूह विलंब है ${\textstyle \tau _{g}(\omega )=-{\frac {d\phi }{d\omega }}}$, इसलिए यह इस प्रकार है कि एक निरंतर समूह विलंब प्राप्त किया जा सकता है यदि उपकरण या माध्यम के स्थानांतरण फ़ंक्शन में रैखिक चरण प्रतिक्रिया होती है (यानी, $\phi (\omega )=\phi (0)-\tau _{g}\omega$ जहां समूह विलंब करता है $\tau _{g}$ एक स्थिरांक है। चरण की गैर-रैखिकता की डिग्री एक स्थिर मूल्य से समूह विलंब के विचलन को इंगित करती है।

सही समय विलंब

एक संचारण उपकरण को वास्तविक समय विलंब (टीटीडी) कहा जाता है यदि समय विलंब विद्युत संकेत की आवृत्ति से स्वतंत्र होता है। टीटीडी दोषरहित और कम-नुकसान, फैलाव मुक्त, पारेषण लाइनों की एक महत्वपूर्ण विशेषता है। टीटीडी एक व्यापक तात्कालिक संकेत बैंडविड्थ संकेत प्रोसेसिंग के लिए अनुमति देता है जिसमें स्पंदित ऑपरेशन के दौरान पल्स ब्रॉडिंग जैसे लगभग कोई संकेत विरूपण नहीं होता है।

यह भी देखें

• ऑडियो सिस्टम माप
• बेसेल फिल्टर
• आंखों का पैटर्न
• समूह वेग - किसी माध्यम में प्रकाश का समूह वेग प्रति इकाई लंबाई समूह विलंब का व्युत्क्रम होता है।

संदर्भ

 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.

बाहरी संबंध

• Discussion of Group Delay in Loudspeakers
• Group Delay Explanations and Applications
• "Introduction to Digital Filters with Audio Applications", Julius O. Smith III, (September 2007 Edition).