संभाव्यता वितरण फिटिंग

संभाव्यता वितरण फिटिंग या पूर्णतः वितरण फिटिंग एक चर घटना के बार-बार माप से संबंधित डेटा की एक श्रृंखला के लिए संभाव्यता वितरण की फिटिंग है। वितरण फिटिंग का उद्देश्य किसी निश्चित अंतराल में घटना की भयावहता की संभावना की भविष्यवाणी करना या घटित होने की आवृत्ति का पूर्वानुमान लगाना है।

कई संभाव्यता वितरण हैं (संभाव्यता वितरण की सूची देखें) जिनमें से कुछ को घटना और वितरण की विशेषताओं के आधार पर, दूसरों की तुलना में डेटा की देखी गई आवृत्ति के अधिक समीप से उपयुक्त किया जा सकता है। यह माना जाता है कि वितरण एक करीबी उपयुक्त देता है जिससे अच्छी भविष्यवाणियाँ होती हैं। इसलिए, वितरण फिटिंग में, किसी को ऐसे वितरण का चयन करने की आवश्यकता होती है जो डेटा के लिए उपयुक्त हो।

वितरण का चयन

माध्य μ और विचरण σ² के आधार पर सममित सामान्य वितरण के विभिन्न आकार

उपयुक्त वितरण का चयन केंद्रीय प्रवृत्ति के संबंध में डेटा सेट की समरूपता की उपस्थिति या अनुपस्थिति पर निर्भर करता है।

सममित वितरण

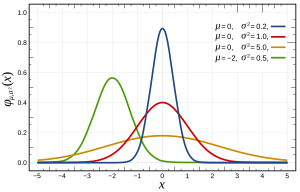
जब डेटा को माध्य के चारों ओर सममित रूप से वितरित किया जाता है, जबकि माध्य से दूर डेटा की घटना की आवृत्ति कम हो जाती है, तो उदाहरण के लिए कोई सामान्य वितरण, लॉजिस्टिक वितरण या छात्र के टी-वितरण का चयन कर सकता है। पहले दो बहुत समान हैं, जबकि अंतिम, एक डिग्री की स्वतंत्रता के साथ, "हेवियर टेल्स" है जिसका अर्थ है कि माध्य से दूर के मान अपेक्षाकृत अधिक बार होते हैं (यानी कर्टोसिस अधिक होता है)। कॉची वितरण भी सममित है।

दाईं ओर विषम (स्केव) वितरण

जब बड़े मान छोटे मानों की तुलना में माध्य से अधिक दूर होते हैं, तो व्यक्ति के दाईं ओर विषम वितरण होता है (अर्थात धनात्मक विषमता होती है), उदाहरण के लिए, कोई व्यक्ति लॉग-सामान्य वितरण का चयन कर सकता है (यानी डेटा के लॉग मान सामान्य रूप से वितरित होते हैं), लॉग-लॉजिस्टिक वितरण (यानी डेटा के लॉग मान लॉजिस्टिक वितरण का पालन करते हैं), गम्बेल वितरण, घातीय वितरण, पारेतो वितरण, वेइबुल वितरण, बूर वितरण, या फ़्रेचेट वितरण। अंतिम चार वितरण बाईं ओर सीमित हैं।

बाएँ और दाएँ विषमता

बायीं ओर विषम वितरण

जब छोटे मान बड़े मानों की तुलना में माध्य से अधिक दूर होते हैं, तो व्यक्ति के बाईं ओर विषम वितरण होता है (यानी ऋणात्मक विषमता होती है), उदाहरण के लिए, व्यक्ति वर्ग-सामान्य वितरण का चयन कर सकता है (अर्थात उस पर लागू सामान्य वितरण डेटा मानों का वर्ग), उलटा (प्रतिबिंबित) गंबेल वितरण, डैगम वितरण (प्रतिबिंबित बूर वितरण), या गोम्पर्ट्ज़ वितरण, जो बाईं ओर घिरा हुआ है।

फिटिंग की तकनीकें

वितरण फिटिंग की निम्नलिखित तकनीकें उपस्थित हैं:

• पैरामीटर विधियाँ, जिनके द्वारा डेटा श्रृंखला से वितरण के मापदंडों की गणना की जाती है। पैरामीट्रिक विधियाँ हैं:
  • क्षणों की विधि (सांख्यिकी)
  • अधिकतम अंतर अनुमान
  • L-क्षणों की विधि
  • अधिकतम संभावना विधि

उदाहरण के लिए, पैरामीटर $\mu$ (अपेक्षा) का अनुमान डेटा के माध्यम से लगाया जा सकता है और पैरामीटर $\sigma ^{2}$(विचरण) का अनुमान डेटा के मानक विचलन से लगाया जा सकता है। माध्य ${\textstyle m=\sum {X}/n}$ के रूप में पाया जाता है, जहां $X$ डेटा मूल्य है और $n$ डेटा की संख्या है, जबकि मानक विचलन की गणना ${\textstyle s={\sqrt {{\frac {1}{n-1}}\sum {(X-m)^{2}}}}}$ के रूप में की जाती है। इन पैरामीटर्स के साथ कई वितरण, उदा. सामान्य वितरण, पूर्णतः परिभाषित हैं।

क्यूमफ़्रेक का उपयोग करके अतिरिक्त आत्मविश्वास बैंड के साथ प्रतिगमन विधि द्वारा सूरीनाम में अक्टूबर में अधिकतम एक दिवसीय वर्षा के लिए संचयी गम्बेल वितरण उपयुक्त किया गया

• संचयी वितरण फ़ंक्शन के परिवर्तन का उपयोग करके प्लॉटिंग स्थिति प्लस प्रतिगमन विश्लेषण, ताकि संचयी संभाव्यता और डेटा के मूल्यों के बीच एक रैखिक संबंध पाया जा सके, जिसे चयनित संभाव्यता वितरण के आधार पर बदलने की भी आवश्यकता हो सकती है। इस विधि में प्लॉटिंग स्थिति द्वारा संचयी संभाव्यता का अनुमान लगाने की आवश्यकता होती है।

उदाहरण के लिए, संचयी गम्बेल वितरण को $Y=aX+b$ पर रेखीयकृत किया जा सकता है, जहां $X$ डेटा चर है और $Y=-\ln(-\ln P)$, $P$ संचयी संभाव्यता होने के साथ, अर्थात संभावना है कि डेटा मान $X$ से कम है। इस प्रकार, $P$ के लिए प्लॉटिंग स्थिति का उपयोग करते हुए, कोई $X$ पर $Y$ के एक रैखिक प्रतिगमन से पैरामीटर $a$ और $b$ पाता है, और गम्बेल वितरण पूरी तरह से परिभाषित होता है।

वितरणों का सामान्यीकरण

सममित वितरण (सामान्य और लॉजिस्टिक की तरह) को उपयुक्त करने के लिए डेटा को लॉगरिदमिक रूप से परिवर्तित करने की प्रथा है, जो कि वितरण का पालन करने वाले डेटा में सकारात्मक रूप से विषम होता है (यानी दाईं ओर विषम होता है, माध्य> मोड के साथ, और दाएं हाथ की पूंछ के साथ जो इससे अधिक लंबी होती है) बाएँ हाथ का पट), लॉगनॉर्मल वितरण और लॉग-लॉजिस्टिक वितरण देखें। एक समान प्रभाव डेटा का वर्गमूल लेकर प्राप्त किया जा सकता है।

किसी भी विषमता के वितरण का पालन करने वाले डेटा में सममित वितरण को उपयुक्त करने के लिए सामान्यतः कोई डेटा को पावर p तक बढ़ा सकता है, जिससे विषमता  धनात्मक होने पर p <1 और विषमता ऋणात्मक होने पर p > 1 हो सकता है। p का इष्टतम मान संख्यात्मक विधि से ज्ञात किया जाना है। संख्यात्मक विधि में पी मानों की एक श्रृंखला को मानना, फिर सभी अनुमानित पी मानों के लिए वितरण फिटिंग प्रक्रिया को बार-बार लागू करना और अंत में p के मान का चयन करना सम्मिलित हो सकता है जिसके लिए मापी गई आवृत्तियों से गणना की गई संभावनाओं के विचलन के वर्गों का योग (ची) सम्मिलित हो सकता है। चुकता) न्यूनतम है, जैसा कमफ़्रीक में किया जाता है।

सामान्यीकरण संभाव्यता वितरण के नम्यता को बढ़ाता है और वितरण फिटिंग में उनकी प्रयोज्यता को बढ़ाता है।

सामान्यीकरण की बहुमुखी प्रतिभा इसे संभव बनाती है, उदाहरण के लिए, लगभग सामान्य रूप से वितरित डेटा सेट को बड़ी संख्या में अलग-अलग संभाव्यता वितरणों में उपयुक्त करना, जबकि ऋणात्मक रूप से विषमता वितरणों को वर्गाकार सामान्य और प्रतिबिंबित गम्बेल वितरणों में उपयुक्त किया जा सकता है।

वैषम्य का व्युत्क्रमण

(ए) गंबेल संभाव्यता वितरण दाईं ओर विषम है और (बी) गंबेल बाईं ओर विषम प्रतिबिंबित है

संचयी वितरण फ़ंक्शन (F) की गणितीय अभिव्यक्ति को इसके पूरक द्वारा प्रतिस्थापित करके विषम वितरण को उलटा (या प्रतिबिंबित) किया जा सकता है: F'=1-F पूरक वितरण फ़ंक्शन (जिसे उत्तरजीविता फ़ंक्शन भी कहा जाता है) प्राप्त करना जो एक दर्पण छवि देता है। इस तरीके से, एक वितरण जो दाईं ओर विषम है, एक ऐसे वितरण में बदल जाता है जो बाईं ओर विषम है और इसके विपरीत।

उदाहरण। धनात्मक रूप से विषम गम्बेल वितरण की एफ-अभिव्यक्ति है: F=exp[-exp{-(X-u)/0.78s}] जहां u मोड है (अर्थात सबसे अधिक बार होने वाला मान) और s मानक विचलन है। गम्बेल वितरण को F'=1-exp[-exp{-(x-u)/0.78s}] का उपयोग करके बदला जा सकता है। यह परिवर्तन व्युत्क्रम, प्रतिबिंबित, या पूरक गम्बेल वितरण उत्पन्न करता है जो ऋणात्मक रूप से विषम वितरण का पालन करने वाली डेटा श्रृंखला में उपयुक्त हो सकता है।

विषम व्युत्क्रमण की तकनीक वितरण फिटिंग के लिए उपलब्ध संभाव्यता वितरणों की संख्या बढ़ाती है और वितरण फिटिंग के अवसरों को बढ़ाती है।

वितरण का स्थानांतरण

कुछ संभाव्यता वितरण, जैसे घातांक, ऋणात्मक डेटा मान (X) का समर्थन नहीं करते हैं। फिर भी, जब ऋणात्मक डेटा उपस्थित होता है, तब भी ऐसे वितरणों का उपयोग X को Y=X-Xm से प्रतिस्थापित करके किया जा सकता है, जहां Xm, X का न्यूनतम मान है। यह प्रतिस्थापन संभाव्यता वितरण के धनात्मक दिशा में बदलाव को दर्शाता है, अर्थात दाईं ओर, क्योंकि Xm ऋणात्मक है. Y की वितरण फिटिंग को पूरा करने के बाद, संबंधित X-मान X=Y+Xm से पाए जाते हैं, जो ऋणात्मक दिशा में, यानी बाईं ओर वितरण के बैक-शिफ्ट का प्रतिनिधित्व करता है।

वितरण स्थानांतरण की तकनीक उचित रूप से उपयुक्त संभाव्यता वितरण खोजने का अवसर बढ़ाती है।

समग्र वितरण

आत्मविश्वास बेल्ट के साथ समग्र (असंतत) वितरण

विकल्प दो अलग-अलग संभाव्यता वितरणों का उपयोग करने के लिए उपस्थित है, निम्न डेटा रेंज के लिए, और उच्च के लिए, उदाहरण के लिए लाप्लास वितरण। श्रेणियाँ ब्रेक-पॉइंट द्वारा अलग की जाती हैं। इस तरह के मिश्रित (असंतत) संभाव्यता वितरण का उपयोग तब उचित हो सकता है जब अध्ययन की गई घटना के लिए डेटा दो अलग-अलग स्थितियों के तहत प्राप्त किया गया हो।

पूर्वानुमान की अनिश्चितता

द्विपद वितरण का उपयोग करके आत्मविश्वास बेल्ट के साथ अनिश्चितता विश्लेषण

उपयुक्त संभाव्यता वितरणों के आधार पर घटना की भविष्यवाणियाँ अनिश्चितता के अधीन हैं, जो निम्नलिखित स्थितियों से उत्पन्न होती हैं:

• घटनाओं का वास्तविक संभाव्यता वितरण उपयुक्त किए गए वितरण से विचलित हो सकता है, क्योंकि देखी गई डेटा श्रृंखला यादृच्छिक त्रुटि के कारण घटना के घटित होने की वास्तविक संभावना का पूरी तरह से प्रतिनिधि नहीं हो सकती है।
• किसी अन्य स्थिति में या भविष्य में घटनाओं की घटना उपयुक्त किए गए वितरण से विचलित हो सकती है क्योंकि यह घटना यादृच्छिक त्रुटि के अधीन भी हो सकती है
• पर्यावरणीय परिस्थितियों में बदलाव से घटना के घटित होने की संभावना में बदलाव हो सकता है।

पहले और दूसरे स्तिथि में अनिश्चितता का अनुमान द्विपद संभाव्यता वितरण के साथ प्राप्त किया जा सकता है, उदाहरण के लिए पे की अधिकता की संभावना (यानी घटना X, X के संदर्भ मूल्य एक्सआर से बड़ी है) और गैर की संभावना का उपयोग करके प्राप्त किया जा सकता है। -अतिरिक्त Pn (अर्थात् घटना X के संदर्भ मान X_r से छोटा या बराबर होने की संभावना, इसे संचयी संभाव्यता भी कहा जाता है)। इस स्तिथि में, केवल दो संभावनाएँ हैं: या तो अति है या अति नहीं है। इस द्वैत के कारण ही द्विपद वितरण लागू होता है।

द्विपद वितरण से कोई पूर्वानुमान अंतराल प्राप्त कर सकता है। ऐसा अंतराल विफलता के जोखिम का भी अनुमान लगाता है, यानी संभावना है कि पूर्वानुमानित घटना अभी भी विश्वास अंतराल से बाहर है। विश्वास या जोखिम विश्लेषण में रिटर्न अवधि T=1/Pe सम्मिलित हो सकती है, जैसा कि जल विज्ञान में किया जाता है।

उपयुक्त की अच्छाई के आधार पर क्रमबद्ध संभाव्यता वितरण की सूची।

जीईवी वितरण को उपयुक्त करने वाले डेटा सेट का हिस्टोग्राम और संभाव्यता घनत्व

उपयुक्तता की अच्छाई

विभिन्न वितरणों की उपयुक्तता की रैंकिंग करके कोई यह आभास प्राप्त कर सकता है कि कौन सा वितरण स्वीकार्य है और कौन सा नहीं।

हिस्टोग्राम और सघनता फलन

संचयी वितरण फलन (सीडीएफ) से कोई हिस्टोग्राम और संभाव्यता घनत्व फलन (पीडीएफ) प्राप्त कर सकता है।

यह भी देखें

• वक्र फिटिंग
• घनत्व अनुमान
• मिश्रण वितरण
• गुणनफल वितरण