प्रायिकता वितरण

For other uses, see वितरण.

संभाव्यता सिद्धांत और आंकड़ों में, संभाव्यता वितरण गणितीय कार्य (गणित) है जो प्रयोग (संभाव्यता सिद्धांत) के लिए विभिन्न संभावित परिणामों की घटना की संभावना देता है। यह इसके नमूना स्थान और घटना की संभावना (संभाव्यता सिद्धांत) (नमूना स्थान के उपसमुच्चय) के संदर्भ में यादृच्छिकता घटना का गणितीय विवरण है।

उदाहरण के लिए, यदि X सिक्का टॉस (प्रयोग) के परिणाम को निरूपित करने के लिए उपयोग किया जाता है, फिर X की संभावना वितरण X = heads के लिए मान 0.5 (2 या 1/2 में 1) और 0.5 ले जाएगा X = टेल (उस निष्पक्ष सिक्के को मानते हुए)। यादृच्छिक घटनाओं के उदाहरणों में कुछ भविष्य की तारीख में मौसम की स्थिति, यादृच्छिक रूप से चयनित व्यक्ति की ऊंचाई, स्कूल में पुरुष छात्रों का अंश, सर्वेक्षण पद्धति के परिणामों का संचालन करना, आदि सम्मिलित हैं।

परिचय

संभावना द्रव्यमान कार्य (पीएमएफ) $p(S)$ योग के लिए संभावना वितरण निर्दिष्ट करता है $S$ दो पासा से मायने रखता है।उदाहरण के लिए, आंकड़ा दिखाता है कि $p(11)=2/36=1/18$।पीएमएफ इस तरह की घटनाओं की संभावनाओं की गणना की अनुमति देता है $P(X>9)=1/12+1/18+1/36=1/6$, और वितरण में अन्य सभी संभावनाएं।

एक संभावना वितरण घटनाओं की संभावनाओं, नमूना स्थान के उपसमुच्चय की संभावनाओं का गणितीय विवरण है।नमूना स्थान, जिसे अधिकांशतः $\Omega$ निरूपित किया जाता है , यादृच्छिक घटना के सभी संभावित परिणामों (संभावना) का समुच्चय (गणित) है;यह कोई भी समुच्चय हो सकता है: वास्तविक संख्याओं का समुच्चय, सदिश (गणित) का समुच्चय, इच्छानुसार गैर-नामांकित मूल्यों का समुच्चय, आदि। उदाहरण के लिए, सिक्का फ्लिप का नमूना स्थान Ω = {heads, tails} होगा ।

यादृच्छिक वेरिएबल के विशिष्ट स्थितियोंके लिए संभाव्यता वितरण को परिभाषित करने के लिए (इसलिए नमूना स्थान को संख्यात्मक समुच्चय के रूप में देखा जा सकता है), असतत और बिल्कुल निरंतर यादृच्छिक वेरिएबल के मध्य अंतर करना आम है।असतत स्थितियोंमें, यह संभावना द्रव्यमान कार्य $p$ को निर्दिष्ट करने के लिए पर्याप्त है प्रत्येक संभावित परिणाम के लिए संभावना प्रदान करना: उदाहरण के लिए, उचित पासा फेंकते समय, छह मान 1 से 6 में से प्रत्येक में संभावना 1/6 होती है।एक घटना की संभावना (संभाव्यता सिद्धांत) को तब उन परिणामों की संभावनाओं का योग माना जाता है जो घटना को संतुष्ट करते हैं;उदाहरण के लिए, घटना की संभावना भी मूल्य रोल करती है

$$p(2)+p(4)+p(6)=1/6+1/6+1/6=1/2.$$

इसके विपरीत, जब यादृच्छिक वेरिएबल निरंतरता से मान लेता है तब सामान्यतः, किसी भी व्यक्तिगत परिणाम में संभावना शून्य होती है और केवल ऐसी घटनाएं होती हैं जिनमें असीम रूप से अनेक परिणाम सम्मिलित होते हैं, जैसे कि अंतराल, सकारात्मक संभावना हो सकती है। उदाहरण के लिए, सुपरमार्केट में हैम के टुकड़े के वजन को मापने पर विचार करें, और मान लें कि मापदंड में स्पष्टता के अनेक अंक हैं।संभावना है कि इसका वजन ठीक 500 & g शून्य है, क्योंकि इसमें कुछ गैर-शून्य दशमलव अंक होंगे।फिर भी, कोई भी गुणवत्ता नियंत्रण में मांग कर सकता है, कि 500 & g हैम के पैकेज;का वजन कम से कम 98% संभावना के साथ 490 & g और 510 & g के मध्य वजन होना चाहिए, और यह मांग माप उपकरणों की स्पष्टता के लिए कम संवेदनशील है।

बाईं ओर संभावना घनत्व फलन दिखाता है।अधिकार संचयी वितरण फलन को दर्शाता है, जिसके लिए मूल्य पर के सामान्तर क्षेत्र के सामान्तर होता है।

बिल्कुल निरंतर संभावना वितरण को अनेक तरीकों से वर्णित किया जा सकता है।संभाव्यता घनत्व फलन किसी भी मूल्य की इनफिनिटिमल्स संभावना का वर्णन करता है, और संभावना है कि किसी दिए गए अंतराल में परिणाम निहित है, एकीकरण (गणित) द्वारा उस अंतराल पर संभावना घनत्व फलन द्वारा गणना की जा सकती है।वितरण का वैकल्पिक विवरण संचयी वितरण फलन के माध्यम से है, जो इस संभावना का वर्णन करता है कि यादृच्छिक वेरिएबल किसी दिए गए मूल्य से बड़ा नहीं है (अर्थात, कुछ $x$ के लिए $P(X<x)$)।संचयी वितरण फलन से संभावना घनत्व फलन के $-\infty$ को $x$ अनुसार क्षेत्र है, जैसा कि चित्र द्वारा दाईं ओर वर्णित है।

सामान्य संभाव्यता परिभाषा

एक संभाव्यता वितरण को विभिन्न रूपों में वर्णित किया जा सकता है, जैसे कि संभावना द्रव्यमान कार्य या संचयी वितरण फलन द्वारा।सबसे सामान्य विवरणों में से एक, जो बिल्कुल निरंतर और असतत वेरिएबल के लिए प्रयुक्त होता है, संभाव्यता फलन के $P\colon {\mathcal {A}}\to \mathbb {R}$ माध्यम से है जिसका इनपुट स्पेस ${\mathcal {A}}$ संबंधित है नमूना स्थान के लिए, और इसके आउटपुट के रूप में वास्तविक संख्या ${\displaystyle [0,1]\subseteq \mathbb {R} }.$ संभावना देता है।

संभाव्यता फलन $P$ नमूना स्थान के तर्क उपसमुच्चय के रूप में ले सकते हैं, जैसा कि सिक्का टॉस उदाहरण में, जहां फलन $P$ ऐसा परिभाषित किया गया था P(heads) = 0.5 और P(tails) = 0.5।चूंकि, यादृच्छिक वेरिएबल के व्यापक उपयोग के कारण, जो नमूना स्थान को संख्याओं के समुच्चय में बदल देते हैं (जैसे, $\mathbb {R}$, $\mathbb {N}$), संभावना वितरण का अध्ययन करना अधिक सामान्य है, जिनके तर्क इन विशेष प्रकार के समुच्चयों (संख्या समुच्चय) के उपसमुच्चय हैं, और इस लेख में वेरिएबल ्चा की गई सभी संभावना वितरण इस प्रकार के हैं।के रूप में निरूपित करना आम है $P(X\in E)$ संभावना है कि वेरिएबल $X$ का निश्चित मूल्य निश्चित घटना से संबंधित है $E$.

उपरोक्त संभाव्यता फलन केवल संभाव्यता वितरण की विशेषता है यदि यह सभी कोल्मोगोरोव स्वयंसिद्ध को संतुष्ट करता है, अर्थात:

1. $P(X\in E)\geq 0\;\forall E\in {\mathcal {A}}$, इसलिए संभावना गैर-ऋणात्मक है
2. $P(X\in E)\leq 1\;\forall E\in {\mathcal {A}}$, इसलिए कोई संभावना $1$ से अधिक नहीं है
3. $P(X\in \bigsqcup _{i}E_{i})=\sum _{i}P(X\in E_{i})$ समुच्चय $\{E_{i}\}$ के किसी भी असंतुष्ट परिवार के लिए उपयोग नही किया जाता है

संभाव्यता फलन की अवधारणा को संभाव्यता स्थान $(X,{\mathcal {A}},P)$ के तत्व के रूप में परिभाषित करके अधिक कठोर बना दिया जाता है , जहाँ $X$ संभावित परिणामों का समुच्चय है, ${\mathcal {A}}$ सभी उपसमुच्चय का समुच्चय है $E\subset X$ जिनकी संभावना को मापा जा सकता है, और $P$ संभावना फलन, या संभाव्यता माप है, जो इन औसत अंकिते के उपसमुच्चय में से प्रत्येक के लिए संभावना प्रदान करता है $E\in {\mathcal {A}}$.

संभाव्यता वितरण सामान्यतः दो वर्गों में से संबंधित हैं। तथा असतत संभावना वितरण उन परिदृश्यों पर प्रयुक्त होता है जहां संभावित परिणामों का समुच्चय असतत संभावना वितरण है (जैसे कि सिक्का टॉस, मरने का रोल) और संभावनाओं को परिणामों की संभावनाओं की असतत सूची द्वारा एन्कोड किया जाता है; इस स्थितियों में असतत संभावना वितरण को संभावना द्रव्यमान कार्य के रूप में जाना जाता है। दूसरी ओर, बिल्कुल निरंतर संभावना वितरण उन परिदृश्यों पर प्रयुक्त होते हैं जहां संभावित परिणामों का समुच्चय निरंतर सीमा (जैसे वास्तविक संख्या) में मूल्यों पर ले जा सकता है, जैसे कि किसी दिए गए दिन पर तापमान।अधिक बिल्कुल निरंतर स्थितियों में संभावनाएं संभाव्यता घनत्व फलन द्वारा वर्णित की जाती हैं, और संभावना वितरण संभावना घनत्व फलन के अभिन्न अंग की परिभाषा के अनुसार है। सामान्य वितरण सामान्यतः बिल्कुल निरंतर संभावना वितरण है।अधिक जटिल प्रयोग किये गये है, जैसे कि निरंतर समय में परिभाषित स्टोकेस्टिक प्रक्रियाओं को सम्मिलित करने वाले, अधिक सामान्य संभावना उपायों के उपयोग की मांग कर सकते हैं।

एक संभाव्यता वितरण का उपयोग किया जाता है जिसका नमूना स्थान एक-आयामी है और (उदाहरण के लिए वास्तविक संख्या, लेबल की सूची, ऑर्डर किए गए लेबल या बाइनरी) को अविभाज्य वितरण कहा जाता है, जबकि वितरण जिसका नमूना स्थान आयाम 2 या 2 से अधिक का सदिश स्थान है, जिसे मल्टीवेरेट वितरण कहा जाता है। अविभाज्य वितरण विभिन्न-विभिन्न मूल्यों पर एकल यादृच्छिक वेरिएबल की संभावनाओं को देता है; एक बहुभिन्नरूपी वितरण (एक संयुक्त संभावना वितरण) यादृच्छिक सदिश की संभावनाएं देता है - दो या अधिक यादृच्छिक वेरिएबल की सूची - मूल्यों के विभिन्न संयोजनों पर ले जाता है। महत्वपूर्ण और सामान्यतः सामना किए जाने वाले एकतरफा संभावना वितरण में द्विपद वितरण, हाइपरजोमेट्रिक वितरण और सामान्य वितरण सम्मिलित हैं। सामान्यतः सामना किया जाने वाला बहुभिन्नरूपी वितरण बहुभिन्नरूपी सामान्य वितरण है।

संभाव्यता फलन, संचयी वितरण फलन, संभाव्यता द्रव्यमान फलन और संभाव्यता घनत्व फलन, क्षण उत्पन्न करने वाले फलन और विशेषता फलन (संभाव्यता सिद्धांत) के अतिरिक्त, संभावना वितरण की पहचान करने के लिए भी काम करते हैं, क्योंकि वे विशिष्ट रूप से अंतर्निहित संचयी वितरण फलन का निर्धारण करते हैं।

सामान्य वितरण की संभाव्यता घनत्व फलन (पीडीएफ), जिसे गाऊसी या बेल वक्र भी कहा जाता है, सबसे महत्वपूर्ण बिल्कुल निरंतर यादृच्छिक वितरण।जैसा कि आंकड़े पर ध्यान दिया गया है, मूल्यों के अंतराल की संभावनाएं वक्र के अनुसार क्षेत्र के अनुरूप हैं।

शब्दावली

संभावना वितरण के विषय पर साहित्य में व्यापक रूप से उपयोग किए जाने वाले कुछ प्रमुख अवधारणाओं और शब्द नीचे सूचीबद्ध हैं।

मूल शर्तें

• यादृच्छिक वेरिएबल : नमूना स्थान से मान लेता है;संभावनाएं बताती हैं कि कौन से मान और मूल्यों के समुच्चय को अधिक संभावना है।
• घटना (संभाव्यता सिद्धांत): यादृच्छिक वेरिएबल के संभावित मूल्यों (परिणामों) का समुच्चय जो निश्चित संभावना के साथ होता है।
• संभाव्यता उपाय या संभाव्यता माप: संभावना $P(X\in E)$ का वर्णन करता है वह घटना $E,$ होता है।
• संचयी वितरण फलन : संभावना का मूल्यांकन करने वाले फलन $X$ से कम या उसके सामान्तर मूल्य लेंगे $x$ यादृच्छिक वेरिएबल के लिए (केवल वास्तविक-मूल्यवान यादृच्छिक वेरिएबल के लिए)।
• क्वांटाइल फलन: संचयी वितरण फलन का उलटा।देता है $x$ ऐसा, संभावना $q$ के साथ , $X$ $x$ अधिक नहीं होगा ।

असतत संभावना वितरण

• असतत संभावना वितरण: अनेक यादृच्छिक वेरिएबल के लिए सूक्ष्म रूप से या गिनती से असीम रूप से अनेक मूल्यों के साथ।
• प्रायिकता द्रव्यमान फलन ( पीमफ ): फलन जो संभावना देता है कि असतत यादृच्छिक वेरिएबल कुछ मूल्य के सामान्तर है।
• आवृत्ति वितरण : तालिका जो विभिन्न परिणामों की आवृत्ति को एक नमूने में प्रदर्शित करती है ।
• सापेक्ष आवृत्ति वितरण: आवृत्ति वितरण जहां प्रत्येक मान को नमूना (आँकड़े) (अर्थात नमूना आकार) में अनेक परिणामों द्वारा विभाजित (सामान्यीकृत) किया गया है।
• श्रेणीबद्ध वितरण: मूल्यों के परिमित समुच्चय के साथ असतत यादृच्छिक वेरिएबल के लिए।

बिल्कुल निरंतर संभावना वितरण

• बिल्कुल निरंतर संभावना वितरण: अनेक यादृच्छिक वेरिएबल के लिए अधिकतम अनेक मूल्यों के साथ।
• प्रायिकता घनत्व फलन ( पीडीफ ) या प्रायिकता घनत्व : फलन जिसका मूल्य किसी भी दिए गए नमूने (या बिंदु) पर नमूना स्थान (यादृच्छिक वेरिएबल द्वारा लिए गए संभावित मूल्यों का समुच्चय) पर है। एक सापेक्ष संभावना 'प्रदान करने के रूप में व्याख्या की जा सकती है कि यादृच्छिक वेरिएबल का मूल्य उस नमूने के सामान्तर होगा।

संबंधित शब्द

• समर्थन (गणित): मान यादृच्छिक वेरिएबल द्वारा गैर-शून्य संभावना के साथ मान लिया जा सकता है।एक यादृच्छिक वेरिएबल $X$ के लिए , इसे कभी -कभी $R_{X}$निरूपित किया जाता है ।
• टेल : यादृच्छिक वेरिएबल की सीमा के करीब क्षेत्र, यदि पीएमएफ या पीडीएफ अपेक्षाकृत कम हैं। सामान्यतः रूप $X>a$, $X<b$ या उसके पश्चात् संघ होता है।
• हेड : वह क्षेत्र जहां पीएमएफ या पीडीएफ अपेक्षाकृत अधिक है। सामान्यतः $a<X<b$ रूप होता है ।
• अपेक्षित मूल्य या मतलब: संभावित मूल्यों का भारित औसत है तथा उनकी संभावनाओं का उपयोग उनके वजन के रूप में;या निरंतर एनालॉग के उपयोग में किया जाता है ।
• माध्य: मूल्य जैसे कि माध्य से कम मानों का समुच्चय, और समुच्चय से अधिक समुच्चय, प्रत्येक में संभावनाएं हैं कि एक-आधा से अधिक नहीं है।
• मोड (सांख्यिकी): असतत यादृच्छिक वेरिएबल के लिए, उच्चतम संभावना के साथ मूल्य;एक बिल्कुल निरंतर यादृच्छिक वेरिएबल के लिए, स्थान जिस पर संभावना घनत्व फलन में स्थानीय शिखर होता है।
• क्वांटाइल: क्यू-क्वांटाइल मान है $x$ ऐसा है कि $P(X<x)=q$।
• विचरण माध्य के बारे में पीएमएफ या पीडीएफ का दूसरा क्षण;वितरण के सांख्यिकीय फैलाव का महत्वपूर्ण उपाय।
• मानक विचलन: विचरण का वर्गमूल, और इसलिए फैलाव का और उपाय।
• सममित संभावना वितरण: कुछ वितरणों की संपत्ति जिसमें वितरण का हिस्सा विशिष्ट मूल्य के बाईं ओर (सामान्यतः माध्यिका) के हिस्से की दर्पण छवि है, जो इसके दाईं ओर है।
• तिरछापन: जिस सीमा तक पीएमएफ या पीडीएफ अपने माध्य के तरफ से झुकता है, उसका उपाय।वितरण का तीसरा मानकीकृत क्षण।
• कर्टोसिस: पीएमएफ या पीडीएफ की पूंछ के मोटापे का उपाय।वितरण का चौथा मानकीकृत क्षण।

संचयी वितरण फलन

एक वास्तविक-मूल्यवान यादृच्छिक वेरिएबल के विशेष स्थितियोंमें, संभाव्यता वितरण को संभावना माप के अतिरिक्त संचयी वितरण फलन द्वारा समान रूप से दर्शाया जा सकता है। एक यादृच्छिक वेरिएबल का संचयी वितरण कार्य $X$ संभावना वितरण के संबंध में $p$ की तरह परिभाषित किया गया है

$$F(x)=P(X\leq x).$$

किसी भी वास्तविक-मूल्यवान यादृच्छिक वेरिएबल के संचयी वितरण फलन में गुण होते हैं:

• <ली स्टाइल = मार्जिन: 0.7REM 0;>$F(x)$ गैर-डिसीजिंग है;
• <ली स्टाइल = मार्जिन: 0.7REM 0;>$F(x)$ सही-निरंतर है;
• <ली स्टाइल = मार्जिन: 0.7REM 0;>$0\leq F(x)\leq 1$;
• <ली स्टाइल = मार्जिन: 0.7REM 0;>$\lim _{x\to -\infty }F(x)=0$ और $\lim _{x\to \infty }F(x)=1$;और
• <ली स्टाइल = मार्जिन: 0.7REM 0;>$\Pr(a<X\leq b)=F(b)-F(a)$।

इसके विपरीत, कोई भी कार्य $F:\mathbb {R} \to \mathbb {R}$ यह उपरोक्त गुणों के पहले चार को संतुष्ट करता है, वास्तविक संख्याओं पर कुछ संभाव्यता वितरण का संचयी वितरण कार्य है। किसी भी संभावना वितरण को असतत संभावना वितरण के योग के रूप में विघटित किया जा सकता है, बिल्कुल निरंतर संभावना वितरण और विलक्षण उपाय, और इस प्रकार कोई भी संचयी वितरण फलन संचयी वितरण कार्यों के अनुसार तीनों के योग के रूप में अपघटन को स्वीकार करता है।

असतत संभावना वितरण

Main article: जन समारोह की संभावना

एक असतत संभावना वितरण की संभावना द्रव्यमान कार्य।सिंगलटन (गणित) की संभावनाएं {1}, {3}, और {7} क्रमशः 0.2, 0.5, 0.3 हैं।इनमें से किसी भी बिंदु से युक्त समुच्चय में संभावना शून्य है।

एक असतत संभावना वितरण का संचयी वितरण कार्य, ...

... निरंतर संभावना वितरण की, ...

... वितरण का जिसमें निरंतर हिस्सा और असतत हिस्सा दोनों है।

एक असतत संभावना वितरण यादृच्छिक वेरिएबल की संभावना वितरण है जो केवल मानों की गिनती योग्य संख्या पर ले जा सकता है (लगभग निश्चित रूप से) जिसका अर्थ है कि किसी भी घटना की संभावना $E$ (परिमित या श्रृंखला (गणित)) योग के रूप में व्यक्त किया जा सकता है:

$$P(X\in E)=\sum _{\omega \in A}P(X=\omega ),$$

जहाँ $A$ गिनती योग्य समुच्चय है। इस प्रकार असतत यादृच्छिक वेरिएबल वास्तव में संभावना द्रव्यमान $p(x)=P(X=x)$ कार्य के साथ हैं । उस स्थितियों में जहां मूल्यों की सीमा अनगिनत अनंत है, इन मानों को संभावनाओं के लिए पर्याप्त तेजी से शून्य तक गिरना होगा। उदाहरण के लिए, उदाहरण के लिए, यदि, यदि $p(n)={\tfrac {1}{2^{n}}}$ के लिए $n=1,2,...$, संभावनाओं का योग होगा $1/2+1/4+1/8+\dots =1$।

एक असतत यादृच्छिक वेरिएबल यादृच्छिक वेरिएबल है जिसका संभाव्यता वितरण असतत है।

सांख्यिकीय मॉडलिंग में उपयोग किए जाने वाले प्रसिद्ध असतत संभावना वितरण में पॉइसन वितरण, बर्नौली वितरण, द्विपद वितरण, ज्यामितीय वितरण, ऋणात्मक द्विपद वितरण और श्रेणीबद्ध वितरण सम्मिलित हैं। जब नमूना (आँकड़े) (टिप्पणियों का समुच्चय) बड़ी जनसंख्या से खींचा जाता है, तब नमूना बिंदुओं में अनुभवजन्य वितरण फलन होता है जो असतत होता है, और जो जनसंख्या वितरण के बारे में जानकारी प्रदान करता है। इसके अतिरिक्त, यूनिफ़ॉर्म डिस्ट्रीब्यूशन (असतत) का उपयोग सामान्यतः कंप्यूटर प्रोग्रामों में किया जाता है जो अनेक विकल्पों के मध्य समान-संभाव्यता यादृच्छिक चयन बनाते हैं।

संचयी वितरण फलन

एक वास्तविक-मूल्यवान असतत यादृच्छिक वेरिएबल को समतुल्य रूप से यादृच्छिक वेरिएबल के रूप में परिभाषित किया जा सकता है जिसका संचयी वितरण फलन केवल कूदने से बढ़ता है-अर्थात, इसका सीडीएफ केवल जहां यह उच्च मूल्य पर कूदता है, और बिना कूद के अंतराल में स्थिर होता है।जिन बिंदुओं पर छलांग लगती है, वे ठीक वे मान हैं जो यादृच्छिक वेरिएबल ले सकते हैं। इस प्रकार संचयी वितरण फलन का रूप है

$$F(x)=P(X\leq x)=\sum _{\omega \leq x}p(\omega ).$$

ध्यान दें कि वे बिंदु जहां सीडीएफ कूदता है सदैव गणना योग्य समुच्चय बनाता है; यह कोई भी गिनती करने योग्य समुच्चय हो सकता है और इस प्रकार वास्तविक संख्याओं में भी घना हो सकता है।

DIRAC डेल्टा प्रतिनिधित्व

एक असतत संभावना वितरण को अधिकांशतः डिराक उपायों पतित वितरण की संभावना वितरण के साथ दर्शाया जाता है। किसी भी परिणाम $\omega$ के लिए , मान लीजिये $\delta _{\omega }$ $\omega$ डिराक उपाय पर केंद्रित हो । असतत संभावना वितरण को देखते हुए, $P(X\in A)=1$ के साथ गणना योग्य समुच्चय $A$ है और संभावना द्रव्यमान कार्य $p$ है।यदि $E$ कोई घटना है, तब

$$P(X\in E)=\sum _{\omega \in A}p(\omega )\delta _{\omega }(E),$$

या संक्षेप में,

$$P_{X}=\sum _{\omega \in A}p(\omega )\delta _{\omega }.$$

इसी तरह, असतत वितरण को डिराक डेल्टा फलन के साथ सामान्यीकृत संभावना घनत्व फलन $f$ के रूप में दर्शाया जा सकता है , जहाँ

$$f(x)=\sum _{\omega \in A}p(\omega )\delta (x-\omega ),$$

जिसका कारणहै

$$P(X\in E)=\int _{E}f(x)\,dx=\sum _{\omega \in A}p(\omega )\int _{E}\delta (x-\omega )=\sum _{\omega \in A\cap E}p(\omega )$$

किसी भी घटना के लिए $E.$

संकेतक-फलन प्रतिनिधित्व

एक असतत यादृच्छिक वेरिएबल $X$ के लिए , मान लीजिये की $u_{0},u_{1},\dots$ जो यह गैर-शून्य संभावना के साथ ले सकते हैं। निरूपित

$$\Omega _{i}=X^{-1}(u_{i})=\{\omega :X(\omega )=u_{i}\},\,i=0,1,2,\dots$$

ये असंतुष्ट समुच्चय हैं, और ऐसे समुच्चयों के लिए

$$P\left(\bigcup _{i}\Omega _{i}\right)=\sum _{i}P(\Omega _{i})=\sum _{i}P(X=u_{i})=1.$$

यह इस बात की संभावना है कि $X$ द्वारा $u_{0},u_{1},\dots$ को छोड़कर कोई भी मान लेने की संभावना शून्य है और इस प्रकार कोई $X$ इस प्रकार लिख सकता है जैसा

$$X(\omega )=\sum _{i}u_{i}1_{\Omega _{i}}(\omega )$$

संभावना शून्य के समुच्चय को छोड़कर, जहां $1_{A}$ $A$ का संकेतक कार्य है । यह असतत यादृच्छिक वेरिएबल की वैकल्पिक परिभाषा के रूप में काम कर सकता है।

एक-बिंदु वितरण

एक विशेष स्थितिया यादृच्छिक वेरिएबल का असतत वितरण है जो केवल निश्चित मूल्य पर ले सकता है;दूसरे शब्दों में, यह नियतात्मक वितरण है।औपचारिक रूप से व्यक्त किया गया, यादृच्छिक वेरिएबल $X$ यदि संभावित परिणाम है तब एक-बिंदु वितरण है $x$ ऐसा है कि $P(X{=}x)=1.$ अन्य सभी संभावित परिणामों में संभावना 0. है। इसका संचयी वितरण फलन 0 से 1 तक तुरंत कूदता है।

बिल्कुल निरंतर संभावना वितरण

Main article: संभाव्यता सघनता फलन

एक पूरी तरह से निरंतर संभावना वितरण वास्तविक संख्याओं के साथ वास्तविक संख्याओं पर संभावना वितरण है, जैसे कि वास्तविक रेखा में संपूर्ण अंतराल, और जहां किसी भी घटना की संभावना को अभिन्न के रूप में व्यक्त किया जा सकता है। अधिक स्पष्ट रूप से, वास्तविक यादृच्छिक वेरिएबल $X$ तब बिल्कुल निरंतर संभावना वितरण है यदि कोई फलन $f:\mathbb {R} \to [0,\infty ]$ है ऐसा कि प्रत्येक अंतराल $[a,b]\subset \mathbb {R}$ के लिए $X$ की से संबंधित $[a,b]$ के संभावना $f$ ऊपर $I$: अभिन्न अंग द्वारा दिया जाता है

$$P\left(a\leq X\leq b\right)=\int _{a}^{b}f(x)\,dx.$$

यह संभाव्यता घनत्व फलन की परिभाषा है, जिससे पूरी तरह से निरंतर संभावना वितरण वास्तव में संभाव्यता घनत्व फलन के साथ हो। विशेष रूप से, $X$ के लिए कोई एकल मूल्य लेने के लिए $a$ (वह है, $a\leq X\leq a$) संभावना शून्य है, क्योंकि ऊपरी और निचली सीमाओं के साथ अभिन्न अंग सदैव शून्य के सामान्तर होता है।यदि अंतराल $[a,b]$ किसी भी औसत अंकिते का समुच्चय $A$ द्वारा प्रतिस्थापित किया जाता है , जो कि समानता के अनुसार अभी भी है:

$$P(X\in A)=\int _{A}f(x)\,dx.$$

एक बिल्कुल निरंतर यादृच्छिक वेरिएबल यादृच्छिक वेरिएबल है जिसका संभाव्यता वितरण बिल्कुल निरंतर है।

पूरी तरह से निरंतर संभावना वितरण के अनेक उदाहरण हैं: जो कि सामान्य वितरण, समान वितरण (निरंतर), ची-वर्ग वितरण | ची-स्क्वर्ड, और संभाव्यता वितरण की सूची या बिल्कुल निरंतर वितरण।

संचयी वितरण फलन

ऊपर परिभाषित के रूप में बिल्कुल निरंतर संभावना वितरण ठीक पूर्ण निरंतरता संचयी वितरण फलन के साथ हैं। इस स्थितियों में, संचयी वितरण $F$ कार्य प्रपत्र है

$$F(x)=P(X\leq x)=\int _{-\infty }^{x}f(t)\,dt$$

जहाँ $f$ वितरण $P$ के संबंध में यादृच्छिक वेरिएबल $X$ का घनत्व है

शब्दावली पर ध्यान दें: बिल्कुल निरंतर वितरण को 'निरंतर वितरण' से अलग किया जाना चाहिए, जो निरंतर संचयी वितरण फलन वाले हैं।हर बिल्कुल निरंतर वितरण निरंतर वितरण है, किन्तुयह सच नहीं है, एकवचन वितरण उपस्थित हैं, जो न तब बिल्कुल निरंतर हैं और न ही असतत हैं और न ही उन का मिश्रण है, और कोई घनत्व नहीं है।एक उदाहरण कैंटर वितरण द्वारा दिया गया है।कुछ लेखक चूंकि सभी वितरणों को निरूपित करने के लिए सतत वितरण शब्द का उपयोग करते हैं, जिनके संचयी वितरण कार्य बिल्कुल निरंतर कार्य हैं, अर्थात निरंतर वितरण के रूप में बिल्कुल निरंतर वितरण को संदर्भित करते हैं। घनत्व कार्यों की अधिक सामान्य परिभाषा के लिए और समकक्ष बिल्कुल निरंतर उपायों को बिल्कुल निरंतर उपाय देखें।

kolmogorov परिभाषा

Main articles: संभाव्यता स्थान and संभाव्यता माप

माप सिद्धांत में | संभावना सिद्धांत के माप-सिद्धांतीय औपचारिकता, यादृच्छिक वेरिएबल को औसत अंकिते का कार्य के रूप में परिभाषित किया गया है $X$ संभावना स्थान से $(\Omega ,{\mathcal {F}},\mathbb {P} )$ औसत अंकिते के स्थान के लिए $({\mathcal {X}},{\mathcal {A}})$।फॉर्म की घटनाओं की संभावनाओं को देखते हुए $\{\omega \in \Omega \mid X(\omega )\in A\}$ संतुष्ट संभाव्यता स्वयंसिद्ध $X$पुष्पक उपाय है $X_{*}\mathbb {P}$ का $X$ , जो संभावना उपाय है $({\mathcal {X}},{\mathcal {A}})$ संतुष्टि देने वाला $X_{*}\mathbb {P} =\mathbb {P} X^{-1}$.

अन्य प्रकार के वितरण

राबिनोविच -फब्रिकेंट समीकरणों के लिए समाधान।समर्थन के निश्चित स्थान (अर्थात, लाल उपसमुच्चय) पर राज्य को देखने की संभावना क्या है?

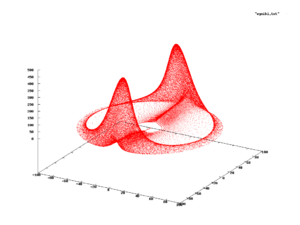
समर्थन के साथ बिल्कुल निरंतर और असतत वितरण $\mathbb {R} ^{k}$ या $\mathbb {N} ^{k}$ घटना के असंख्य को मॉडल करने के लिए बेहद उपयोगी हैं,चूंकि अधिकांश व्यावहारिक वितरण अपेक्षाकृत सरल उपसमुच्चय पर समर्थित होते हैं, जैसे कि हाइपरक्यूब या बॉल (गणित)।चूंकि, यह सदैव स्थितिया नहीं होता है, और समर्थन के साथ घटनाएं उपस्थित हैं जो वास्तव में जटिल घटता हैं $\gamma :[a,b]\rightarrow \mathbb {R} ^{n}$ कुछ स्थान के अंदर $\mathbb {R} ^{n}$ या इसी के समान।इन स्थितियोंं में, संभावना वितरण को इस तरह की वक्र की छवि पर समर्थित किया जाता है, और इसके लिए बंद सूत्र खोजने के अतिरिक्त अनुभवजन्य रूप से निर्धारित किए जाने की संभावना है।

एक उदाहरण को दाईं ओर के आंकड़े में दिखाया गया है, जो विभेदक समीकरणों की प्रणाली के विकास को प्रदर्शित करता है (जिसे सामान्यतः राबिनोविच -फब्रिकेंट समीकरणों के रूप में जाना जाता है) का उपयोग प्लाज्मा (भौतिकी) में लैंगमुइर तरंगों के व्यवहार को मॉडल करने के लिए किया जा सकता है। जब इस घटना का अध्ययन किया जाता है, तब उपसमुच्चय से देखे गए राज्यों को लाल रंग में इंगित किया जाता है।तब कोई यह पूछ सकता है कि लाल उपसमुच्चय की निश्चित स्थिति में राज्य को देखने की संभावना क्या है;यदि ऐसी संभावना उपस्थित है, तब इसे प्रणाली की संभावना माप कहा जाता है।

इस तरह का जटिल समर्थन गतिशील प्रणालियों में काफी बार दिखाई देता है।यह स्थापित करना सरल नहीं है कि प्रणाली में संभावना उपाय है, और मुख्य समस्या निम्नलिखित है।होने देना $t_{1}\ll t_{2}\ll t_{3}$ समय में इंस्टेंट हो और $O$ समर्थन का उपसमुच्चय;यदि प्रणालीके लिए संभावना उपाय उपस्थित है, तब कोई समुच्चय के अंदर राज्यों को देखने की आवृत्ति की उम्मीद करेगा $O$ अंतराल में समान होगा $[t_{1},t_{2}]$ और $[t_{2},t_{3}]$, जो नहीं हो सकता है;उदाहरण के लिए, यह साइन के समान दोलन कर सकता है, $\sin(t)$, किसकी सीमा कब $t\rightarrow \infty$ अभिसरण नहीं करता है।औपचारिक रूप से, माप केवल तभी उपस्थित होता है जब सापेक्ष आवृत्ति की सीमा तब होती है जब प्रणालीको अनंत भविष्य में देखा जाता है। डायनेमिक प्रणाली की शाखा जो संभाव्यता माप के अस्तित्व का अध्ययन करती है वह है एर्गोडिक सिद्धांत।

ध्यान दें कि इन स्थितियोंं में भी, संभावना वितरण, यदि यह उपस्थित है, तब भी इस बात पर निर्भर करता है कि समर्थन क्रमशः या गिनती योग्य है या नहीं, इस पर निर्भर करता है।

यादृच्छिक संख्या पीढ़ी

Main article: छद्म-यादृच्छिक संख्या नमूनाकरण

अधिकांश एल्गोरिदम स्यूडोरेंडोम नंबर जनरेटर पर आधारित होते हैं जो संख्याओं का उत्पादन करता है $X$ जो समान रूप से आधे-खुले अंतराल में वितरित किए जाते हैं [0, 1)।ये यादृच्छिक वेरिएबल $X$ फिर कुछ एल्गोरिथ्म के माध्यम से नया यादृच्छिक वेरिएबल बनाने के लिए बदल दिया जाता है जो आवश्यक संभावना वितरण होता है।समान छद्म-यादृच्छिकता के इस स्रोत के साथ, किसी भी यादृच्छिक वेरिएबल की वास्तविकता उत्पन्न की जा सकती है। उदाहरण के लिए, मान लीजिए $U$ कुछ के लिए यादृच्छिक बर्नौली वेरिएबल का निर्माण करने के लिए 0 और 1 के मध्य समान वितरण है $0<p<1$, हम परिभाषित करते हैं

$$X={\begin{cases}1,&{\text{if }}U<p\\0,&{\text{if }}U\geq p\end{cases}}$$

ताकि

$$\Pr(X=1)=\Pr(U<p)=p,\quad \Pr(X=0)=\Pr(U\geq p)=1-p.$$

इस यादृच्छिक वेरिएबल एक्स में पैरामीटर के साथ बर्नौली वितरण है $p$.ध्यान दें कि यह असतत यादृच्छिक वेरिएबल का परिवर्तन है।

एक वितरण फलन के लिए $F$ बिल्कुल निरंतर यादृच्छिक वेरिएबल में से, बिल्कुल निरंतर यादृच्छिक वेरिएबल का निर्माण किया जाना चाहिए। $F^{\mathit {inv}}$का उलटा कार्य $F$, वर्दी वेरिएबल से संबंधित है $U$:

$${U\leq F(x)}={F^{\mathit {inv}}(U)\leq x}.$$

उदाहरण के लिए, मान लें कि यादृच्छिक वेरिएबल है जिसमें घातीय वितरण है $F(x)=1-e^{-\lambda x}$ निर्माण किया जाना चाहिए।

$${\begin{aligned}F(x)=u&\Leftrightarrow 1-e^{-\lambda x}=u\\[2pt]&\Leftrightarrow e^{-\lambda x}=1-u\\[2pt]&\Leftrightarrow -\lambda x=\ln(1-u)\\[2pt]&\Leftrightarrow x={\frac {-1}{\lambda }}\ln(1-u)\end{aligned}}$$

इसलिए $F^{\mathit {inv}}(u)={\frac {-1}{\lambda }}\ln(1-u)$ और अगर $U$ $U(0,1)$ वितरण, फिर यादृच्छिक वेरिएबल $X$ द्वारा परिभाषित किया गया है $X=F^{\mathit {inv}}(U)={\frac {-1}{\lambda }}\ln(1-U)$।यह घातीय वितरण है $\lambda$.

सांख्यिकीय सिमुलेशन (मोंटे कार्लो विधि) में लगातार समस्या स्यूडोरेंडोमनेस की पीढ़ी है। छद्म-यादृच्छिक संख्या जो दिए गए तरीके से वितरित की जाती हैं।

सामान्य संभावना वितरण और उनके अनुप्रयोग

For a more comprehensive list, see संभाव्यता वितरण की सूची.

संभाव्यता वितरण और यादृच्छिक वेरिएबल की अवधारणा जो वे वर्णन करते हैं कि संभाव्यता सिद्धांत के गणितीय अनुशासन और सांख्यिकी विज्ञान के विज्ञान को रेखांकित करता है।लगभग किसी भी मूल्य में प्रसार या परिवर्तनशीलता होती है जिसे जनसंख्या में मापा जा सकता है (जैसे लोगों की ऊंचाई, धातु की स्थायित्व, बिक्री वृद्धि, यातायात प्रवाह, आदि);लगभग सभी माप कुछ आंतरिक त्रुटि के साथ किए जाते हैं;भौतिकी में, अनेक प्रक्रियाओं को संभावित रूप से वर्णित किया जाता है, गैसों के गतिज सिद्धांत से मौलिक कणों के क्वांटम यांत्रिक विवरण तक।इन और अनेक अन्य कारणों के लिए, सरल संख्या अधिकांशतः मात्रा का वर्णन करने के लिए अपर्याप्त होती है, जबकि संभावना वितरण अधिकांशतः अधिक उपयुक्त होते हैं।

निम्नलिखित कुछ सबसे सामान्य संभावना वितरणों की सूची है, जिसे वे संबंधित प्रक्रिया के प्रकार द्वारा समूहीकृत करते हैं।अधिक संपूर्ण सूची के लिए, संभाव्यता वितरण की सूची देखें, जो परिणाम की प्रकृति द्वारा माना जाता है (असतत, बिल्कुल निरंतर, बहुभिन्नरूपी, आदि)

नीचे दिए गए सभी एकतरफा वितरण एकल रूप से वेरिएबल म पर हैं;यही है, यह माना जाता है कि मान ही बिंदु के आसपास क्लस्टर करते हैं।व्यवहार में, वास्तव में देखी गई मात्रा अनेक मूल्यों के आसपास क्लस्टर हो सकती है।इस तरह की मात्रा को मिश्रण वितरण का उपयोग करके मॉडलिंग की जा सकती है।

रैखिक विकास (जैसे त्रुटियां, ऑफसमुच्चय)

• सामान्य वितरण (गौसियन वितरण), ऐसी मात्रा के लिए;सबसे अधिक उपयोग किया जाने वाला बिल्कुल निरंतर वितरण

घातीय वृद्धि (जैसे कीमत, आय, आबादी)

• लॉग-सामान्य वितरण, ऐसी एकल मात्रा के लिए जिसका लॉग सामान्य वितरण वितरित है
• Pareto वितरण, ऐसी एकल मात्रा के लिए जिसका लॉग घातांक वितरण वितरित है;प्रोटोटाइप पावर लॉ डिस्ट्रीब्यूशन

समान रूप से वितरित मात्रा

• असतत वर्दी वितरण, मूल्यों के परिमित समुच्चय के लिए (जैसे कि मेला मरने का परिणाम)
• निरंतर समान वितरण, बिल्कुल लगातार वितरित मूल्यों के लिए

बर्नौली परीक्षण (हाँ/नहीं घटना, किसी दिए गए संभाव्यता के साथ)

• मूलभूत वितरण:
  • बर्नौली वितरण, एकल बर्नौली परीक्षण के परिणाम के लिए (जैसे सफलता/विफलता, हाँ/नहीं)
  • द्विपद वितरण, सकारात्मक घटनाओं की संख्या (जैसे सफलताओं, हाँ वोट, आदि) के लिए स्वतंत्र (सांख्यिकी) घटनाओं की निश्चित कुल संख्या दी गई है
  • ऋणात्मक द्विपद वितरण, द्विपद-प्रकार की टिप्पणियों के लिए, किन्तु जहां ब्याज की मात्रा निश्चित संख्या में होने से पहले विफलताओं की संख्या है
  • ज्यामितीय वितरण, द्विपद-प्रकार की टिप्पणियों के लिए किन्तु जहां ब्याज की मात्रा पहली सफलता से पहले विफलताओं की संख्या है; ऋणात्मक द्विपद वितरण का विशेष स्थितिया
• एक परिमित जनसंख्या पर नमूना योजनाओं से संबंधित:
  • हाइपरजोमेट्रिक वितरण, सकारात्मक घटनाओं की संख्या (जैसे सफलताओं, हाँ वोट, आदि) के लिए कुल घटनाओं की निश्चित संख्या को देखते हुए, प्रतिस्थापन के बिना नमूने का उपयोग करना
  • बीटा-बिनोमियल वितरण, सकारात्मक घटनाओं की संख्या (जैसे सफलताओं, हाँ वोट, आदि) के लिए कुल घटनाओं की निश्चित संख्या दी गई, प्लायला कलश मॉडल का उपयोग करके नमूनाकरण (कुछ अर्थों में, प्रतिस्थापन के बिना नमूने के विपरीत)

श्रेणीबद्ध परिणाम (के साथ घटनाएं) K संभावित परिणाम)

• श्रेणीबद्ध वितरण, एकल श्रेणीगत परिणाम के लिए (जैसे सर्वेक्षण में हाँ/नहीं/संभवतः); बर्नौली वितरण का सामान्यीकरण
• बहुराष्ट्रीय वितरण, प्रत्येक प्रकार के श्रेणीबद्ध परिणामों की संख्या के लिए, कुल परिणामों की निश्चित संख्या को देखते हुए; द्विपद वितरण का सामान्यीकरण
• बहुभिन्नरूपी हाइपरजोमेट्रिक वितरण, बहुराष्ट्रीय वितरण के समान, किन्तु प्रतिस्थापन के बिना नमूने का उपयोग करना हाइपरजोमेट्रिक वितरण का सामान्यीकरण

पॉइसन प्रक्रिया (किसी दिए गए दर के साथ स्वतंत्र रूप से होने वाली घटनाएं)

• पॉइसन वितरण, समय की अवधि में पॉइसन-प्रकार की घटनाओं की संख्या के लिए
• घातीय वितरण, अगले पॉइसन-प्रकार की घटना से पहले के समय के लिए
• गामा वितरण, अगले पॉइसन K - प्रकार की घटनाओं से पहले के समय के लिए

सामान्य रूप से वितरित घटकों के साथ सदिश का निरपेक्ष मान

• रेले वितरण, गॉसियन वितरित ऑर्थोगोनल घटकों के साथ सदिश परिमाण के वितरण के लिए। गॉसियन वास्तविक और काल्पनिक घटकों के साथ आरएफ संकेत में रेले वितरण पाए जाते हैं।
• राइस वितरण, रेले वितरण का सामान्यीकरण जहां स्थिर पृष्ठभूमि संकेत घटक है। मल्टीपैथ प्रसार के कारण और गैर-शून्य एनएमआर संकेत पर ध्वनि भ्रष्टाचार के साथ एमआर छवियों में रेडियो सिग्नल के रेनियन लुप्त होने में पाया गया।

सामान्य रूप से वितरित मात्रा वर्गों के योग के साथ संचालित

• ची-वर्ग वितरण, वर्ग मानक सामान्य वेरिएबल के योग का वितरण उपयोगी उदा।सामान्य रूप से वितरित नमूनों के नमूना विचरण के बारे में अनुमान के लिए (ची-स्क्वर्ड परीक्षण देखें)
• छात्र का टी वितरण, मानक सामान्य वेरिएबल के अनुपात का वितरण और स्केल ची चुकता वितरण वेरिएबल का वर्गमूल; अज्ञात विचरण के साथ सामान्य रूप से वितरित नमूनों के माध्य के बारे में अनुमान के लिए उपयोगी (छात्र का टी-टेस्ट देखें)
• एफ-वितरण, दो स्केल ची चुकता वितरण वेरिएबल के अनुपात का वितरण उपयोगी उदा। ऐसे अनुमानों के लिए जिसमें वेरिएंट की तुलना करना या आर-स्क्वेयर सम्मिलित करना सम्मिलित है (चुकता पियर्सन उत्पाद-पल सहसंबंध गुणांक)

के रूप में बायेसियन इनवेंशन में पूर्व वितरण के रूप में

Main article: पूर्व संयुग्मित करें

• बीटा वितरण, एकल संभावना के लिए (0 और 1 के मध्य वास्तविक संख्या) बर्नौली वितरण और द्विपद वितरण के लिए संयुग्मन
• गामा वितरण, गैर-ऋणात्मक स्केलिंग पैरामीटर के लिए एक पॉइसन वितरण या घातीय वितरण के दर पैरामीटर के लिए संयुग्मन, सामान्य वितरण, आदि के स्पष्ट (सांख्यिकी) (उलटा विचरण), आदि।
• डिरिचलेट वितरण, संभावनाओं के सदिश के लिए जो 1 के लिए राशि होनी चाहिए; श्रेणीबद्ध वितरण और बहुराष्ट्रीय वितरण के लिए संयुग्म बीटा वितरण का सामान्यीकरण
• विशार्ट वितरण, सममित गैर-ऋणात्मक निश्चित आव्युह के लिए; बहुभिन्नरूपी सामान्य वितरण के सहसंयोजक आव्युह के व्युत्क्रम के लिए संयुग्म गामा वितरण का सामान्यीकरण

संभावना वितरण के कुछ विशेष अनुप्रयोग

• कैश लैंग्वेज मॉडल और अन्य सांख्यिकीय भाषा मॉडल प्राकृतिक भाषा प्रसंस्करण में उपयोग किए जाने वाले विशेष शब्दों और शब्द अनुक्रमों की घटना के लिए संभावनाएं प्रदान करने के लिए संभावना वितरण के माध्यम से ऐसा करते हैं।
• क्वांटम यांत्रिकी में, किसी दिए गए बिंदु पर कण को खोजने की संभावना घनत्व उस बिंदु पर कण की तरंग के परिमाण के वर्ग के लिए आनुपातिक है (जन्म के नियम देखें)। इसलिए, कण की स्थिति की संभावना वितरण कार्य द्वारा वर्णित किया गया है ${\textstyle P_{a\leq x\leq b}(t)=\int _{a}^{b}dx\,|\Psi (x,t)|^{2}}$, संभावना है कि कण की स्थिति x अंतराल में होगा a ≤ x ≤ b आयाम में, और आयाम तीन में समान ट्रिपल अभिन्न।यह क्वांटम यांत्रिकी का प्रमुख सिद्धांत है।
• पावर-फ्लो अध्ययन में संभाव्य लोड प्रवाह इनपुट वेरिएबल की अनिश्चितताओं को संभाव्यता वितरण के रूप में बताता है और संभावना वितरण की अवधि में बिजली प्रवाह गणना भी प्रदान करता है।
• पिछले आवृत्ति वितरण जैसे कि उष्णकटिबंधीय चक्रवात, ओले, घटनाओं के मध्य समय, आदि के आधार पर प्राकृतिक घटनाओं की भविष्यवाणी की ।

फिटिंग

This section is an excerpt from संभाव्यता वितरण फिटिंग.[edit]

संभाव्यता वितरण फिटिंग या पूर्णतः वितरण फिटिंग एक चर घटना के बार-बार माप से संबंधित डेटा की एक श्रृंखला के लिए संभाव्यता वितरण की फिटिंग है। वितरण फिटिंग का उद्देश्य किसी निश्चित अंतराल में घटना की भयावहता की संभावना की भविष्यवाणी करना या घटित होने की आवृत्ति का पूर्वानुमान लगाना है।

कई संभाव्यता वितरण हैं (संभाव्यता वितरण की सूची देखें) जिनमें से कुछ को घटना और वितरण की विशेषताओं के आधार पर, दूसरों की तुलना में डेटा की देखी गई आवृत्ति के अधिक समीप से उपयुक्त किया जा सकता है। यह माना जाता है कि वितरण एक करीबी उपयुक्त देता है जिससे अच्छी भविष्यवाणियाँ होती हैं। इसलिए, वितरण फिटिंग में, किसी को ऐसे वितरण का चयन करने की आवश्यकता होती है जो डेटा के लिए उपयुक्त हो।

यह भी देखें

• सशर्त संभाव्यता वितरण
• संयुक्त संभावना वितरण
• अर्धसंभाव्यता वितरण
• अनुभवजन्य संभावना
• हिस्टोग्राम
• रीमैन-स्टिल्टजे इंटीग्रल या एप्लिकेशन टू प्रोबेबिलिटी थ्योरी | रीमैन-स्टिल्टजेस इंटीग्रल एप्लिकेशन टू प्रोबेबिलिटी थ्योरी

सूची

• संभाव्यता वितरण की सूची
• सांख्यिकीय विषयों की सूची

संदर्भ

स्रोत

• den Dekker, A. J.; Sijbers, J. (2014). "चुंबकीय अनुनाद छवियों में डेटा वितरण: एक समीक्षा". Physica Medica. 30 (7): 725–741. doi:10.1016/j.ejmp.2014.05.002. PMID 25059432.
• Vapnik, Vladimir Naumovich (1998). सांख्यिकीय शिक्षण सिद्धांत. John Wiley and Sons.

बाहरी कड़ियाँ

• "Probability distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Field Guide to Continuous Probability Distributions, Gavin E. Crooks.

संभाव्यता वितरण श्रेणी: गणितीय और मात्रात्मक तरीके (अर्थशास्त्र)]