कांस्टेंट शीफ

गणित में, टोपोलॉजिकल स्पेस पर स्थिर शीफ़ $X$ एक सेट से संबंधित (गणित) $A$ पर एक शीफ (गणित) है $X$ जिसके डंठल (शेफ) सभी बराबर हों $A$. द्वारा निरूपित किया जाता है ${\underline {A}}$ या $A_{X}$. मान के साथ स्थिर प्रीशीफ $A$ वह प्रीशीफ़ है जो प्रत्येक गैर-रिक्त खुले सेट को असाइन करता है $X$ मूल्य $A$, और जिनके सभी प्रतिबंध मानचित्र पहचान मानचित्र हैं $A\to A$. से संबंधित निरंतर शीफ़ $A$ से जुड़े निरंतर प्रीशीफ़ का शीफ़ीकरण है $A$. यह शीफ स्थानीय स्थिरांक के शीफ से पहचान करता है $A$-मूल्यवान कार्य चालू $X$. कुछ मामलों में, सेट $A$ किसी वस्तु से प्रतिस्थापित किया जा सकता है (श्रेणी सिद्धांत) $A$ किसी श्रेणी में (गणित) ${\textbf {C}}$ (उदाहरण के लिए जब ${\textbf {C}}$ [[एबेलियन समूहों की श्रेणी]] है, या क्रमविनिमेय वलय की श्रेणी है)।

एबेलियन समूहों के निरंतर शीव विशेष रूप से शीफ़ कोहोमोलोजी में गुणांक के रूप में दिखाई देते हैं।

बुनियादी बातें

होने देना $X$ एक टोपोलॉजिकल स्पेस बनें, और $A$ एक सेट। स्थिर शीफ के अनुभाग ${\underline {A}}$ एक खुले सेट पर $U$ निरंतर कार्यों के रूप में व्याख्या की जा सकती है $U\to A$, कहाँ $A$ असतत टोपोलॉजी दी गई है। अगर $U$ स्थान जुड़ा हुआ है, तो ये स्थानीय रूप से स्थिर कार्य स्थिर हैं। अगर $f:X\to \{{\text{pt}}\}$ एक-बिंदु स्थान के लिए अद्वितीय मानचित्र (गणित) है और $A$ पर एक पुलिंदा माना जाता है $\{{\text{pt}}\}$, फिर उलटा छवि शीफ $f^{-1}A$ स्थिर पूल है ${\underline {A}}$ पर $X$. का शीफ़ स्थान ${\underline {A}}$ प्रक्षेपण मानचित्र है $A$ (कहाँ $X\times A\to X$ असतत टोपोलॉजी दी गई है)।

एक विस्तृत उदाहरण

दो-बिंदु असतत स्थान पर लगातार प्रीशेफ़

दो-बिंदु असतत टोपोलॉजिकल स्पेस

होने देना $X$ दो बिंदुओं से युक्त टोपोलॉजिकल स्पेस बनें $p$ और $q$ असतत टोपोलॉजी के साथ. $X$ चार खुले सेट हैं: $\varnothing ,\{p\},\{q\},\{p,q\}$. के खुले सेट के पांच गैर-तुच्छ समावेशन $X$ चार्ट में दिखाया गया है.

पर एक प्रीशीफ $X$ के चार खुले सेटों में से प्रत्येक के लिए एक सेट चुनता है $X$ और नौ समावेशन मानचित्रों में से प्रत्येक के लिए एक प्रतिबंध मानचित्र (पांच गैर-तुच्छ समावेशन और चार तुच्छ समावेशन)। मान के साथ स्थिर प्रीशीफ ${\textbf {Z}}$, जिसे हम निरूपित करेंगे $F$, वह प्रीशीफ़ है जो सभी चार सेटों को चुनता है ${\textbf {Z}}$, पूर्णांक, और सभी प्रतिबंध मानचित्र पहचान होंगे। $F$ एक फ़नकार है, इसलिए एक प्रीशीफ़ है, क्योंकि यह स्थिर है। $F$ ग्लूइंग सिद्धांत को संतुष्ट करता है, लेकिन यह एक शीफ नहीं है क्योंकि यह खाली सेट पर स्थानीय पहचान सिद्धांत को विफल करता है। ऐसा इसलिए है क्योंकि खाली सेट सेट के खाली परिवार द्वारा कवर किया जाता है: रिक्त रूप से, कोई भी दो खंड $F$ खाली परिवार में किसी भी सेट तक सीमित होने पर खाली सेट पर बराबर होते हैं। इसलिए स्थानीय पहचान स्वयंसिद्ध का तात्पर्य यह होगा कि कोई भी दो खंड $F$ खाली सेट पर बराबर हैं, लेकिन यह सच नहीं है।

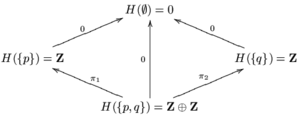
एक समान प्रीशीफ $G$ जो खाली सेट पर स्थानीय पहचान सिद्धांत को संतुष्ट करता है उसका निर्माण निम्नानुसार किया जाता है। होने देना $G(\varnothing )=0$, जहां 0 एक-तत्व सेट है। सभी गैर-रिक्त सेटों पर, दें $G$ मूल्य ${\textbf {Z}}$. खुले सेटों के प्रत्येक समावेशन के लिए, $G$ यदि छोटा सेट खाली है, तो या तो अद्वितीय मानचित्र को 0 पर लौटाता है, या पहचान मानचित्र को चालू करता है ${\textbf {Z}}$.

स्थिर शीफ़ के लिए मध्यवर्ती चरण

ध्यान दें कि खाली सेट के लिए स्थानीय पहचान सिद्धांत के परिणामस्वरूप, खाली सेट से जुड़े सभी प्रतिबंध मानचित्र उबाऊ हैं। यह खाली सेट के लिए स्थानीय पहचान स्वयंसिद्ध को संतुष्ट करने वाले किसी भी प्रीशीफ के लिए और विशेष रूप से किसी भी शीफ के लिए सच है।

$G$ एक पृथक प्रीशीफ़ है (अर्थात, स्थानीय पहचान सिद्धांत को संतुष्ट करता है), लेकिन इसके विपरीत $F$ यह ग्लूइंग सिद्धांत को विफल कर देता है। $\{p,q\}$ दो खुले सेटों द्वारा कवर किया गया है $\{p\}$ और $\{q\}$, और इन सेटों में खाली चौराहा है। पर एक अनुभाग $\{p\}$ या पर $\{q\}$ का एक तत्व है ${\textbf {Z}}$, अर्थात यह एक संख्या है। एक अनुभाग चुनें $m$ ऊपर $\{p\}$ और $n$ ऊपर $\{q\}$, और मान लीजिये $m\neq n$. क्योंकि $m$ और $n$ एक ही तत्व को 0 से अधिक तक सीमित रखें $\varnothing$, ग्लूइंग स्वयंसिद्ध को एक अद्वितीय अनुभाग के अस्तित्व की आवश्यकता होती है $s$ पर $G(\{p,q\})$ जो कि प्रतिबंधित है $m$ पर $\{p\}$ और $n$ पर $\{q\}$. लेकिन क्योंकि प्रतिबंध मानचित्र से $\{p,q\}$ को $\{p\}$ पहचान है, $s=m$, और इसी तरह $s=n$, इसलिए $m=n$, एक विरोधाभास.

दो-बिंदु टोपोलॉजिकल स्पेस पर लगातार शीफ

$G(\{p,q\})$ दोनों के बारे में जानकारी रखने के लिए बहुत छोटा है $\{p\}$ और $\{q\}$. इसे बड़ा करने के लिए ताकि यह ग्लूइंग सिद्धांत को संतुष्ट कर सके, चलो $H(\{p,q\})=\mathbf {Z} \oplus \mathbf {Z}$. होने देना $\pi _{1}$ और $\pi _{2}$ दो प्रक्षेपण मानचित्र बनें $\mathbf {Z} \oplus \mathbf {Z} \to \mathbf {Z}$. परिभाषित करना $H(\{p\})={\text{im}}(\pi _{1})=\mathbf {Z}$ और $H(\{q\})={\text{im}}(\pi _{2})=\mathbf {Z}$. शेष खुले सेट और समावेशन के लिए, आइए $H$ बराबर $G$. $H$ एक शीफ है जिसे निरंतर शीफ ऑन कहा जाता है $X$ मूल्य के साथ ${\textbf {Z}}$. क्योंकि ${\textbf {Z}}$ एक वलय है और सभी प्रतिबंध मानचित्र वलय समरूपताएँ हैं, $H$ क्रमविनिमेय छल्लों का एक समूह है।

यह भी देखें

• स्थानीय रूप से स्थिर शीफ

संदर्भ

• Section II.1 of Hartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics, vol. 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157
• Section 2.4.6 of Tennison, B.R. (1975), Sheaf theory, ISBN 978-0-521-20784-3