डबल-प्रिसिजन फ़्लोटिंग-पॉइंट फॉर्मेट
डबल-प्रिसिजन फ़्लोटिंग-पॉइंट प्रारूप (जिसे कभी-कभी एफपी64 या फ्लोट64 भी कहा जाता है) एक फ़्लोटिंग-पॉइंट नंबर प्रारूप है, जो प्रायः कंप्यूटर मेमोरी में 64 बिट्स रखता है; यह एक फ़्लोटिंग मूलांक बिंदु का उपयोग करके संख्यात्मक मानों की एक विस्तृत गतिशील श्रृंखला का प्रतिनिधित्व करता है।
फ़्लोटिंग पॉइंट का उपयोग भिन्नात्मक मानों को दर्शाने के लिए किया जाता है, या जब निश्चित-बिंदु (समान बिट चौड़ाई) द्वारा प्रदान की जाने वाली व्यापक रेंज की आवश्यकता होती है, भले ही परिशुद्धता की कीमत पर हो। दोहरी परिशुद्धता को तब चुना जा सकता है जब एकल-परिशुद्धता फ़्लोटिंग-पॉइंट प्रारूप की सीमा या परिशुद्धता अपर्याप्त होगी।
आईईई 754-2008 मानकीकरण में, 64-बिट बेस-2 प्रारूप को आधिकारिक रूप से बाइनरी64 कहा जाता है; आईईईई 754-1985 में इसे डबल कहा गया। आईईईई 754 अतिरिक्त फ़्लोटिंग-पॉइंट प्रारूप निर्दिष्ट करता है, जिसमें 32-बिट बेस-2 एकल परिशुद्धता और, हाल ही में, बेस-10 प्रतिनिधित्व सम्मिलित हैं।
सिंगल और डबल-प्रिसिजन फ़्लोटिंग-पॉइंट डेटा प्रकार प्रदान करने वाली पहली प्रोग्रामिंग भाषाओं में से एक फोरट्रान थी। आईईईई 754-1985 को व्यापक रूप से अपनाने से पहले, फ्लोटिंग-पॉइंट डेटा प्रकारों का प्रतिनिधित्व और गुण कंप्यूटर निर्माता और कंप्यूटर मॉडल और प्रोग्रामिंग-भाषा कार्यान्वयनकर्ताओं द्वारा किए गए निर्णयों पर निर्भर थे। उदाहरण के लिए, जीडब्ल्यू-बेसिक का डबल-प्रिसिजन डेटा टाइप 64-बिट एमबीएफ फ़्लोटिंग-पॉइंट प्रारूप था।
| Floating-point formats |
|---|
| IEEE 754 |
|
| Other |
आईईईई 754 डबल-प्रिसिजन बाइनरी फ़्लोटिंग-पॉइंट प्रारूप: बाइनरी64
इसके प्रदर्शन और बैंडविड्थ लागत के बाद भी, सिंगल-प्रिसिजन फ़्लोटिंग पॉइंट पर इसकी व्यापक रेंज के कारण डबल-प्रिसिजन बाइनरी फ़्लोटिंग-पॉइंट पीसी पर साधारणतः उपयोग किया जाने वाला प्रारूप है। इसे प्रायः डबल के नाम से जाना जाता है। आईईईई 754 मानक एक बाइनरी64 को इस प्रकार निर्दिष्ट करता है:
- साइन बिट: 1 बिट
- घातांक: 11 बिट्स
- अपूर्णांश परिशुद्धता: 53 बिट्स (52 स्पष्ट रूप से संग्रहीत)
साइन बिट संख्या का चिह्न निर्धारित करता है (इसमें यह भी सम्मिलित है कि जब यह संख्या शून्य है, जो चिह्नित है)।
घातांक क्षेत्र पूर्वाग्रहित रूप में 0 से 2047 तक 11-बिट अचिहिनत इन्टिजर है: 1023 का घातांक मान वास्तविक शून्य का प्रतिनिधित्व करता है। घातांक -1022 से +1023 तक होते हैं क्योंकि -1023 (सभी 0s) और +1024 (सभी 1s) के घातांक विशेष संख्याओं के लिए आरक्षित होते हैं।
53-बिट अपूर्णांश परिशुद्धता 15 से 17 सार्थक दशमलव अंकों की सटीकता (2−53 ≈ 1.11 × 10−16) देती है। यदि अधिकतम 15 सार्थक अंकों वाली एक दशमलव स्ट्रिंग को सामान्य संख्या देते हुए आईईईई 754 डबल-प्रिसिजन प्रारूप में परिवर्तित किया जाता है, और फिर समान अंकों की संख्या के साथ दशमलव स्ट्रिंग में परिवर्तित किया जाता है, तो अंतिम परिणाम मूल स्ट्रिंग से मेल खाना चाहिए। यदि आईईईई 754 डबल-प्रिसिजन संख्या को कम से कम 17 सार्थक अंकों के साथ दशमलव स्ट्रिंग में परिवर्तित किया जाता है, और फिर वापस डबल-प्रिसिजन निरूपण में परिवर्तित किया जाता है, तो अंतिम परिणाम मूल संख्या से मेल खाना चाहिए।[1]
प्रारूप को अपूर्णांश के साथ लिखा गया है और इसमें मान 1 का एक अंतर्निहित इन्टिजर बिट है (विशेष डेटा को छोड़कर, नीचे घातांक एन्कोडिंग देखें)। फ्रैक्शन (एफ) के 52 बिट्स के मेमोरी प्रारूप में प्रदर्शित होने के साथ, कुल परिशुद्धता 53 बिट्स (लगभग 16 दशमलव अंक, 53 log10(2) ≈ 15.955) है। बिट्स को इस प्रकार रखा गया है:
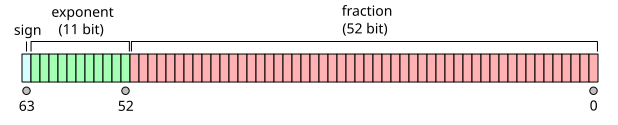 किसी दिए गए पूर्वाग्रह घातांक और एक 52-बिट फ्रैक्शन के साथ दिए गए 64-बिट डबल-प्रिसिजन डेटम द्वारा ग्रहण किया गया वास्तविक मान है
किसी दिए गए पूर्वाग्रह घातांक और एक 52-बिट फ्रैक्शन के साथ दिए गए 64-बिट डबल-प्रिसिजन डेटम द्वारा ग्रहण किया गया वास्तविक मान है
या
252=4,503,599,627,370,496 और 253=9,007,199,254,740,992 के बीच प्रतिनिधित्व योग्य संख्याएँ बिल्कुल इन्टिजर हैं। अगली श्रेणी के लिए, 253 से 254 तक, हर संख्या को 2 से गुणा किया जाता है, इसलिए प्रतिनिधित्व योग्य संख्याएँ सम संख्याएँ हैं, आदि। इसके विपरीत, 251से 252 तक की पिछली श्रेणी के लिए, अंतर 0.5 है, आदि।
2 से सीमा में संख्याओं के एक अंश के रूप में अंतरnसे 2n+1 2 हैn−52. किसी संख्या को निकटतम निरूपण योग्य संख्या (मशीन ईपीएसलॉन) में पूर्णांकित करते समय अधिकतम सापेक्ष पूर्णांकन त्रुटि 2 होती है−53.
घातांक की 11 बिट चौड़ाई 10 के बीच संख्याओं के प्रतिनिधित्व की अनुमति देती है−308और 10308, पूर्ण 15-17 दशमलव अंकों की सटीकता के साथ। परिशुद्धता से समझौता करके, असामान्य प्रतिनिधित्व लगभग 5 × 10 तक के छोटे मानों की भी अनुमति देता है−324.
प्रतिपादक एन्कोडिंग
डबल-प्रिसिजन बाइनरी फ़्लोटिंग-पॉइंट एक्सपोनेंट को ऑफसेट-बाइनरी प्रतिनिधित्व का उपयोग करके एन्कोड किया गया है, जिसमें शून्य ऑफसेट 1023 है; आईईईई 754 मानक में प्रतिपादक पूर्वाग्रह के रूप में भी जाना जाता है। ऐसे अभ्यावेदन के उदाहरण होंगे:
e =000000000012=00116=1:
|
(smallest exponent for normal numbers) | ||
e =011111111112=3ff16=1023:
|
(zero offset) | ||
e =100000001012=40516=1029:
|
|||
e =111111111102=7fe16=2046:
|
(highest exponent) |
प्रतिपादक 00016 और 7ff16 एक विशेष अर्थ है:
000000000002=00016एक हस्ताक्षरित शून्य (यदि एफ = 0) और असामान्य संख्याओं (यदि एफ ≠ 0) का प्रतिनिधित्व करने के लिए उपयोग किया जाता है; और111111111112=7ff16अनंत को दर्शाने के लिए उपयोग किया जाता है|∞ (यदि F = 0) और NaNs (यदि F ≠ 0),
जहाँ F महत्व का भिन्नात्मक भाग है। सभी बिट पैटर्न वैध एन्कोडिंग हैं।
उपरोक्त अपवादों को छोड़कर, संपूर्ण दोहरी-परिशुद्धता संख्या का वर्णन इस प्रकार किया गया है:
असामान्य संख्याओं (e = 0) के मामले में दोहरी-परिशुद्धता संख्या का वर्णन इस प्रकार किया गया है:
एंडियननेस
दोहरे-सटीक उदाहरण
| 0 01111111111 00000000000000000000000000000000000000000000000000002 ≙ 3FF0 0000 0000 000016 ≙ +20 × 1 = 1 |
| 0 01111111111 00000000000000000000000000000000000000000000000000012 ≙ 3FF0 0000 0000 000116 ≙ +20 × (1 + 2−52) ≈ 1.0000000000000002, the smallest number > 1 |
| 0 01111111111 00000000000000000000000000000000000000000000000000102 ≙ 3FF0 0000 0000 000216 ≙ +20 × (1 + 2−51) ≈ 1.0000000000000004 |
| 0 10000000000 00000000000000000000000000000000000000000000000000002 ≙ 4000 0000 0000 000016 ≙ +21 × 1 = 2 |
| 1 10000000000 00000000000000000000000000000000000000000000000000002 ≙ C000 0000 0000 000016 ≙ −21 × 1 = −2 |
| 0 10000000000 10000000000000000000000000000000000000000000000000002 ≙ 4008 0000 0000 000016 ≙ +21 × 1.12 = 112 = 3 |
| 0 10000000001 00000000000000000000000000000000000000000000000000002 ≙ 4010 0000 0000 000016 ≙ +22 × 1 = 1002 = 4 |
| 0 10000000001 01000000000000000000000000000000000000000000000000002 ≙ 4014 0000 0000 000016 ≙ +22 × 1.012 = 1012 = 5 |
| 0 10000000001 10000000000000000000000000000000000000000000000000002 ≙ 4018 0000 0000 000016 ≙ +22 × 1.12 = 1102 = 6 |
| 0 10000000011 01110000000000000000000000000000000000000000000000002 ≙ 4037 0000 0000 000016 ≙ +24 × 1.01112 = 101112 = 23 |
| 0 01111111000 10000000000000000000000000000000000000000000000000002 ≙ 3F88 0000 0000 000016 ≙ +2−7 × 1.12 = 0.000000112 = 0.01171875 (3/256) |
| 0 00000000000 00000000000000000000000000000000000000000000000000012 ≙ 0000 0000 0000 000116 ≙ +2−1022 × 2−52 = 2−1074 ≈ 4.9406564584124654 × 10−324 (Min. subnormal positive double) |
| 0 00000000000 11111111111111111111111111111111111111111111111111112 ≙ 000F FFFF FFFF FFFF16 ≙ +2−1022 × (1 − 2−52) ≈ 2.2250738585072009 × 10−308 (Max. subnormal double) |
| 0 00000000001 00000000000000000000000000000000000000000000000000002 ≙ 0010 0000 0000 000016 ≙ +2−1022 × 1 ≈ 2.2250738585072014 × 10−308 (Min. normal positive double) |
| 0 11111111110 11111111111111111111111111111111111111111111111111112 ≙ 7FEF FFFF FFFF FFFF16 ≙ +21023 × (1 + (1 − 2−52)) ≈ 1.7976931348623157 × 10308 (Max. Double) |
| 0 00000000000 00000000000000000000000000000000000000000000000000002 ≙ 0000 0000 0000 000016 ≙ +0 |
| 1 00000000000 00000000000000000000000000000000000000000000000000002 ≙ 8000 0000 0000 000016 ≙ −0 |
| 0 11111111111 00000000000000000000000000000000000000000000000000002 ≙ 7FF0 0000 0000 000016 ≙ +∞ (positive infinity) |
| 1 11111111111 00000000000000000000000000000000000000000000000000002 ≙ FFF0 0000 0000 000016 ≙ −∞ (negative infinity) |
| 0 11111111111 00000000000000000000000000000000000000000000000000012 ≙ 7FF0 0000 0000 000116 ≙ NaN (sNaN on most processors, such as x86 and ARM) |
| 0 11111111111 10000000000000000000000000000000000000000000000000012 ≙ 7FF8 0000 0000 000116 ≙ NaN (qNaN on most processors, such as x86 and ARM) |
| 0 11111111111 11111111111111111111111111111111111111111111111111112 ≙ 7FFF FFFF FFFF FFFF16 ≙ NaN (an alternative encoding of NaN) |
| 0 01111111101 01010101010101010101010101010101010101010101010101012 = 3FD5 5555 5555 555516 ≙ +2−2 × (1 + 2−2 + 2−4 + ... + 2−52) ≈ 1/3 |
| 0 10000000000 10010010000111111011010101000100010000101101000110002 = 4009 21FB 5444 2D1816 ≈ pi |
NaN#Encoding आईईईई फ़्लोटिंग पॉइंट में पूरी तरह से निर्दिष्ट नहीं हैं और प्रोसेसर पर निर्भर हैं। अधिकांश प्रोसेसर, जैसे कि x86 परिवार और एआरएम वास्तुकला परिवार प्रोसेसर, एक शांत NaN को इंगित करने के लिए महत्व क्षेत्र के सबसे महत्वपूर्ण बिट का उपयोग करते हैं; आईईईई 754 द्वारा इसकी अनुशंसा की जाती है। PA-RISC प्रोसेसर सिग्नलिंग NaN को इंगित करने के लिए बिट का उपयोग करते हैं।
डिफ़ॉल्ट रूप से, 1/3 महत्व में बिट्स की विषम संख्या के कारण, एकल परिशुद्धता की तरह ऊपर की बजाय नीचे की ओर गोल किया जाता है।
और अधिक विस्तार में:
हेक्साडेसिमल प्रतिनिधित्व को देखते हुए 3FD5 5555 5555 555516, चिह्न = 0 घातांक = 3FD16 =1021 घातांक पूर्वाग्रह = 1023 (स्थिर मान; ऊपर देखें) भिन्न = 5 5555 5555 555516
मान = 2(घातांक - घातांक पूर्वाग्रह) × 1.अंश - ध्यान दें कि भिन्न को यहां दशमलव में परिवर्तित नहीं किया जाना चाहिए
= 2−2 × (15 5555 5555 555516 × 2−52)
= 2−54 × 15 5555 5555 555516
= 0.333333333333333314829616256247390992939472198486328125
≈ 1/3
डबल-सटीक अंकगणित के साथ निष्पादन गति
डबल-प्रिसिजन फ़्लोटिंग-पॉइंट वेरिएबल्स का उपयोग प्रायः उनके एकल प्रिसिजन समकक्षों के साथ काम करने की तुलना में धीमा होता है। कंप्यूटिंग का एक क्षेत्र जहां यह एक विशेष मुद्दा है, जीपीयू पर चलने वाला समानांतर कोड है। उदाहरण के लिए, एNVIDIA के CUDA प्लेटफ़ॉर्म का उपयोग करते समय, हार्डवेयर के आधार पर, सिंगल-प्रिसिजन फ़्लोटिंग-पॉइंट प्रारूप का उपयोग करके की गई गणनाओं की तुलना में दोहरी परिशुद्धता वाली गणनाओं को पूरा होने में 2 से 32 गुना अधिक समय लग सकता है।[2] इसके अतिरिक्त, कई गणितीय कार्यों (उदाहरण के लिए, पाप, कॉस, एटैन 2, लॉग, एक्सपी और एसक्यूआरटी) को सटीक डबल-सटीक परिणाम देने के लिए अधिक गणना की आवश्यकता होती है, और इसलिए धीमी होती है।
पूर्णांक मानों पर परिशुद्धता सीमाएँ
- -2 से पूर्णांक53से 253 (−9,007,199,254,740,992 से 9,007,199,254,740,992) को सटीक रूप से दर्शाया जा सकता है
- 2 के बीच पूर्णांक53और 254 = 18,014,398,509,481,984, 2 के गुणज तक (सम संख्या)
- 2 के बीच पूर्णांक54और 255 = 36,028,797,018,963,968, 4 के गुणज तक
कार्यान्वयन
डबल्स को कई प्रोग्रामिंग भाषाओं में अलग-अलग तरीकों से लागू किया जाता है जैसे कि निम्नलिखित। केवल गतिशील परिशुद्धता वाले प्रोसेसर पर, जैसे कि SSE2 के बिना x86 (या जब संगतता उद्देश्य के लिए SSE2 का उपयोग नहीं किया जाता है) और डिफ़ॉल्ट रूप से उपयोग की जाने वाली विस्तारित परिशुद्धता के साथ, सॉफ़्टवेयर को कुछ आवश्यकताओं को पूरा करने में कठिनाई हो सकती है।
सी और सी++
C और C++ विभिन्न प्रकार के C डेटा प्रकार#बेसिक प्रकार प्रदान करते हैं। मानकों द्वारा दोहरी परिशुद्धता की आवश्यकता नहीं है (आईईईई 754 अंकगणित को कवर करने वाले सी99 के वैकल्पिक अनुबंध एफ को छोड़कर), लेकिन अधिकांश प्रणालियों पर, double प्रकार दोहरी परिशुद्धता से मेल खाता है। हालाँकि, डिफ़ॉल्ट रूप से विस्तारित परिशुद्धता के साथ 32-बिट x86 पर, कुछ कंपाइलर सी मानक के अनुरूप नहीं हो सकते हैं या अंकगणित राउंडिंग#डबल राउंडिंग से पीड़ित हो सकता है।[3]
फोरट्रान
फोरट्रान कई पूर्णांक और वास्तविक प्रकार और 64-बिट प्रकार प्रदान करता है real64, फोरट्रान के आंतरिक मॉड्यूल के माध्यम से पहुंच योग्य iso_fortran_env, दोहरी परिशुद्धता से मेल खाती है।
सामान्य लिस्प
कॉमन लिस्प शॉर्ट-फ्लोट, सिंगल-फ्लोट, डबल-फ्लोट और लॉन्ग-फ्लोट प्रकार प्रदान करता है। अधिकांश कार्यान्वयन अन्य प्रकार के उपयुक्त पर्यायवाची शब्दों के साथ सिंगल-फ्लोट्स और डबल-फ्लोट्स प्रदान करते हैं। आईईईई 754 के अनुसार, सामान्य लिस्प फ़्लोटिंग-पॉइंट अंडरफ्लो और ओवरफ़्लो और सटीक फ़्लोटिंग-पॉइंट अपवाद को पकड़ने के लिए अपवाद प्रदान करता है। ANSI मानक में कोई अनंतता और NaN का वर्णन नहीं किया गया है, हालांकि, कई कार्यान्वयन इन्हें एक्सटेंशन के रूप में प्रदान करते हैं।
जावा
संस्करण 1.2 से पहले जावा (प्रोग्रामिंग भाषा) पर, प्रत्येक कार्यान्वयन को आईईईई 754 के अनुरूप होना था। संस्करण 1.2 ने x87 जैसे प्लेटफार्मों के लिए मध्यवर्ती गणनाओं में अतिरिक्त सटीकता लाने के लिए कार्यान्वयन की अनुमति दी। इस प्रकार सख्त आईईईई 754 संगणनाओं को लागू करने के लिए एक संशोधक strictfp पेश किया गया था। जावा 17 में सख्त फ़्लोटिंग पॉइंट बहाल कर दिया गया है।[4]
एकमा स्क्रिप्ट
जैसा कि ईसीएमएस्क्रिप्ट मानक द्वारा निर्दिष्ट किया गया है, जावास्क्रिप्ट (प्रोग्रामिंग भाषा) में सभी अंकगणित डबल-प्रिसिजन फ़्लोटिंग-पॉइंट अंकगणित का उपयोग करके किया जाएगा।[5]
JSON
JSON डेटा एन्कोडिंग प्रारूप संख्यात्मक मानों का समर्थन करता है, और जिस व्याकरण के लिए संख्यात्मक अभिव्यक्तियाँ अनुरूप होनी चाहिए, उसमें एन्कोड किए गए संख्याओं की सटीकता या सीमा पर कोई सीमा नहीं है। हालाँकि, आरएफसी 8259 सलाह देता है कि, चूंकि आईईईई 754 बाइनरी64 नंबर व्यापक रूप से कार्यान्वित हैं, इसलिए जेएसओएन प्रसंस्करण कार्यान्वयन द्वारा अच्छी अंतरसंचालनीयता प्राप्त की जा सकती है यदि वे बाइनरी64 ऑफ़र की तुलना में अधिक सटीकता या सीमा की अपेक्षा नहीं करते हैं।[6]
यह भी देखें
- आईईईई 754, फ्लोटिंग-पॉइंट अंकगणित के लिए आईईईई मानक
- डी संकेतन (वैज्ञानिक संकेतन)
नोट्स और संदर्भ
- ↑ William Kahan (1 October 1997). "Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic" (PDF). Archived (PDF) from the original on 8 February 2012.
- ↑ "Nvidia's New Titan V Pushes 110 Teraflops From A Single Chip". Tom's Hardware (in English). 2017-12-08. Retrieved 2018-11-05.
- ↑ "Bug 323 – optimized code gives strange floating point results". gcc.gnu.org. Archived from the original on 30 April 2018. Retrieved 30 April 2018.
- ↑ Darcy, Joseph D. "JEP 306: Restore Always-Strict Floating-Point Semantics". Retrieved 2021-09-12.
- ↑ ECMA-262 ECMAScript Language Specification (PDF) (5th ed.). Ecma International. p. 29, §8.5 The Number Type. Archived (PDF) from the original on 2012-03-13.
- ↑ "जावास्क्रिप्ट ऑब्जेक्ट नोटेशन (JSON) डेटा इंटरचेंज प्रारूप". Internet Engineering Task Force. December 2017. Retrieved 2022-02-01.
श्रेणी:बाइनरी अंकगणित श्रेणी:कंप्यूटर अंकगणित श्रेणी:फ़्लोटिंग पॉइंट प्रकार