टिमसॉर्ट

From Vigyanwiki
Revision as of 10:10, 7 July 2023 by alpha>Indicwiki (Created page with "{{Short description|Hybrid sorting algorithm based on insertion sort and merge sort}} {{Use dmy dates|date=April 2016}} {{Infobox Algorithm | class = [[Sorting algorithm]...")
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

टिमसॉर्ट
ClassSorting algorithm
Data structureArray
Worst-case performance[1][2]
Best-case performance[3]
Average performance
Worst-case space complexity

टिमसॉर्ट एक हाइब्रिड एल्गोरिदम है, :श्रेणी:स्थिर छँटाई एल्गोरिथ्म, मर्ज़ सॉर्ट और सम्मिलन सॉर्ट से प्राप्त, कई प्रकार के वास्तविक दुनिया डेटा पर अच्छा प्रदर्शन करने के लिए डिज़ाइन किया गया है। इसे टिम पीटर्स (सॉफ्टवेयर इंजीनियर) द्वारा 2002 में पायथन (प्रोग्रामिंग भाषा) में उपयोग के लिए लागू किया गया था। एल्गोरिदम पहले से ही ऑर्डर किए गए डेटा के अनुक्रमों को ढूंढता है (चलता है) और शेष को अधिक कुशलता से सॉर्ट करने के लिए उनका उपयोग करता है। यह कुछ मानदंडों के पूरा होने तक रन को मर्ज करके किया जाता है। टिमसॉर्ट संस्करण 2.3 से पायथन का मानक सॉर्टिंग एल्गोरिदम रहा है। इसका उपयोग जावा 7 में गैर-आदिम प्रकार के सरणियों को सॉर्ट करने के लिए भी किया जाता है,[4] एंड्रॉइड (ऑपरेटिंग सिस्टम) पर,[5] जीएनयू ऑक्टेव में,[6] V8 (जावास्क्रिप्ट इंजन) पर,[7] स्विफ्ट (प्रोग्रामिंग भाषा),[8] और जंग (प्रोग्रामिंग भाषा)।[9] यह पीटर मैकलरॉय के 1993 के पेपर ऑप्टिमिस्टिक सॉर्टिंग एंड इंफॉर्मेशन थ्योरेटिक कॉम्प्लेक्सिटी की तकनीकों का उपयोग करता है।[10]


ऑपरेशन

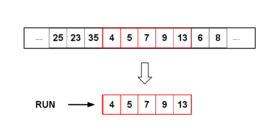
टिमसॉर्ट को लगातार ऑर्डर किए गए तत्वों के रन का लाभ उठाने के लिए डिज़ाइन किया गया था जो पहले से ही अधिकांश वास्तविक दुनिया डेटा, प्राकृतिक रन में मौजूद हैं। यह डेटा एकत्रित करने वाले तत्वों को रनों में पुनरावृत्त करता है और साथ ही उन रनों को एक स्टैक में रखता है। जब भी स्टैक के शीर्ष पर रन टिमसॉर्ट#मर्ज मानदंड से मेल खाते हैं, तो उन्हें मर्ज कर दिया जाता है। यह तब तक चलता रहता है जब तक कि सभी डेटा का पता नहीं लगा लिया जाता; फिर, सभी रन को एक समय में दो में मिला दिया जाता है और केवल एक क्रमबद्ध रन बचता है। निश्चित आकार की उप-सूचियों को मर्ज करने के बजाय ऑर्डर किए गए रन को मर्ज करने का लाभ यह है कि यह पूरी सूची को सॉर्ट करने के लिए आवश्यक तुलनाओं की कुल संख्या को कम कर देता है।

प्रत्येक रन का एक न्यूनतम आकार होता है, जो इनपुट के आकार पर आधारित होता है और एल्गोरिदम की शुरुआत में परिभाषित किया जाता है। यदि कोई रन इस न्यूनतम रन आकार से छोटा है, तो न्यूनतम रन आकार तक पहुंचने तक रन में अधिक तत्व जोड़ने के लिए सम्मिलन सॉर्ट का उपयोग किया जाता है।

मर्ज मानदंड

रन को स्टैक (डेटा संरचना) में डाला जाता है। अगर |Z| ≤ |Y| + |X|, फिर X और Y को मर्ज कर दिया जाता है और स्टैक पर प्रतिस्थापित कर दिया जाता है। इस प्रकार, विलय तब तक जारी रहता है जब तक कि सभी रन संतुष्ट न हो जाएं i. |Z| > |Y| + |X| और ii. |Y| > |X|.

टिमसॉर्ट एक स्थिर सॉर्टिंग एल्गोरिदम है (समान कुंजी वाले तत्वों का क्रम रखा जाता है) और संतुलित मर्ज करने का प्रयास करता है (एक मर्ज इस प्रकार समान आकार के रन को मर्ज करता है)।

सॉर्टिंग स्थिरता प्राप्त करने के लिए, केवल लगातार रन को मर्ज किया जाता है। दो गैर-लगातार रन के बीच, रन के अंदर एक ही कुंजी वाला एक तत्व हो सकता है। उन दो रनों को मर्ज करने से समान कुंजियों का क्रम बदल जाएगा। इस स्थिति का उदाहरण ([] क्रमबद्ध रन हैं): [1 2 2] 1 4 2 [0 1 2]

संतुलित मर्ज की खोज में, टिमसॉर्ट स्टैक के शीर्ष पर तीन रन, एक्स, वाई, जेड पर विचार करता है, और इनवेरिएंट को बनाए रखता है:

  1. |Z| > |Y| + |X|
  2. |Y| > |X|[11]

यदि इनमें से किसी भी अपरिवर्तनीय का उल्लंघन किया जाता है, तो Y को X या Z में से छोटे के साथ विलय कर दिया जाता है और अपरिवर्तनीयों की फिर से जाँच की जाती है। एक बार जब अपरिवर्तनीय पकड़ में आ जाते हैं, तो डेटा में एक नए रन की खोज शुरू हो सकती है।[12] संतुलन के लिए विलय में देरी, सीपीयू कैश में रन की ताजा घटना का फायदा उठाने और मर्ज निर्णयों को अपेक्षाकृत सरल बनाने के बीच समझौता बनाए रखते हुए ये अपरिवर्तनीय मर्ज को लगभग संतुलित बनाए रखते हैं।

ओवरहेड स्थान मर्ज करें

मर्ज करने के लिए, टिमसॉर्ट छोटे ऐरे (इस चित्रण में X) के तत्वों को अस्थायी मेमोरी में कॉपी करता है, फिर तत्वों को अंतिम क्रम में X और Y के संयुक्त स्थान में सॉर्ट और भरता है।

मूल मर्ज सॉर्ट कार्यान्वयन यथास्थान नहीं है और इसमें N (डेटा आकार) का एक स्थान ओवरहेड है। इन-प्लेस मर्ज सॉर्ट कार्यान्वयन मौजूद हैं, लेकिन इसमें बहुत अधिक समय लगता है। एक मध्य अवधि प्राप्त करने के लिए, टिमसॉर्ट एन की तुलना में छोटे समय ओवरहेड और छोटे स्थान ओवरहेड के साथ एक मर्ज सॉर्ट करता है।

सबसे पहले, टिमसॉर्ट उस स्थान को खोजने के लिए एक बाइनरी खोज करता है जहां दूसरे रन का पहला तत्व पहले ऑर्डर किए गए रन में डाला जाएगा, इसे क्रम में रखते हुए। फिर, यह उस स्थान को खोजने के लिए उसी एल्गोरिदम को निष्पादित करता है जहां पहले रन के अंतिम तत्व को दूसरे ऑर्डर किए गए रन में डाला जाएगा, इसे क्रम में रखते हुए। इन स्थानों से पहले और बाद के तत्व पहले से ही अपने सही स्थान पर हैं और उन्हें विलय करने की आवश्यकता नहीं है। फिर, दो रन के शेष तत्वों में से छोटे को अस्थायी मेमोरी में कॉपी किया जाता है, और तत्वों को बड़े रन के साथ अब खाली स्थान में विलय कर दिया जाता है। यदि पहला रन छोटा है, तो मर्ज शुरुआत में शुरू होता है; यदि दूसरा छोटा है, तो मर्ज अंत में शुरू होता है। यह अनुकूलन सामान्य मामले में आवश्यक तत्व आंदोलनों की संख्या, चलने का समय और अस्थायी स्थान को कम कर देता है।

उदाहरण: दो रन [1, 2, 3, 6, 10] और [4, 5, 7, 9, 12, 14, 17] को मर्ज किया जाना चाहिए। ध्यान दें कि दोनों रन पहले से ही अलग-अलग क्रमबद्ध हैं। दूसरे रन का सबसे छोटा तत्व 4 है और इसके क्रम को बनाए रखने के लिए इसे पहले रन के चौथे स्थान पर जोड़ना होगा (यह मानते हुए कि रन की पहली स्थिति 1 है)। पहले रन का सबसे बड़ा तत्व 10 है और इसके क्रम को बनाए रखने के लिए इसे दूसरे रन के पांचवें स्थान पर जोड़ना होगा। इसलिए, [1, 2, 3] और [12, 14, 17] पहले से ही अपनी अंतिम स्थिति में हैं और जिन रन में तत्वों की गतिविधियों की आवश्यकता होती है वे हैं [6, 10] और [4, 5, 7, 9]। इस ज्ञान के साथ, हमें केवल 4 के बजाय 2 आकार का एक अस्थायी बफर आवंटित करने की आवश्यकता है।

विलय की दिशा

विलय दोनों दिशाओं में किया जा सकता है: बाएँ से दाएँ, जैसा कि पारंपरिक मर्जसॉर्ट में होता है, या दाएँ से बाएँ।

मर्ज के दौरान सरपट दौड़ने वाला मोड

तत्वों (नीले तीर द्वारा इंगित) की तुलना की जाती है और छोटे तत्व को उसकी अंतिम स्थिति (लाल तीर द्वारा इंगित) पर ले जाया जाता है।

रन R1 और R2 का एक व्यक्तिगत विलय एक रन से चुने गए लगातार तत्वों की गिनती रखता है। जब यह संख्या न्यूनतम सरपट दौड़ने की सीमा (min_gallop) तक पहुंच जाती है, तो टिमसॉर्ट का मानना ​​​​है कि यह संभावना है कि उस रन से अभी भी कई लगातार तत्वों का चयन किया जा सकता है और सरपट मोड में स्विच किया जा सकता है। आइए मान लें कि R1 इसे ट्रिगर करने के लिए ज़िम्मेदार है। इस मोड में, एल्गोरिदम रन R1 में रन R2 के अगले तत्व x के लिए एक घातीय खोज करता है, जिसे सरपट खोज के रूप में भी जाना जाता है। यह दो चरणों में किया जाता है: पहले चरण में सीमा का पता लगाया जाता है (2क − 1, 2k+1 - 1) जहां x है। दूसरा चरण पहले चरण में पाई गई सीमा में तत्व x के लिए बाइनरी खोज करता है। सरपट मोड रन में तत्वों के बीच अंतराल के पैटर्न के अनुसार मर्ज एल्गोरिदम को अनुकूलित करने का एक प्रयास है।

सभी लाल तत्व नीले से छोटे हैं (यहाँ, 21)। इस प्रकार उन्हें एक टुकड़े में अंतिम सरणी में ले जाया जा सकता है।

सरपट दौड़ना हमेशा कारगर नहीं होता. कुछ मामलों में सरपट दौड़ने वाले मोड में साधारण रैखिक खोज की तुलना में अधिक तुलना की आवश्यकता होती है। डेवलपर द्वारा किए गए बेंचमार्क के अनुसार, सरपट दौड़ना तभी फायदेमंद होता है जब एक रन का प्रारंभिक तत्व दूसरे रन के पहले सात तत्वों में से एक न हो। इसका तात्पर्य 7 की प्रारंभिक सीमा से है। सरपट दौड़ने वाले मोड की कमियों से बचने के लिए, दो क्रियाएं की जाती हैं: (1) जब सरपट दौड़ने को बाइनरी खोज एल्गोरिदम की तुलना में कम कुशल पाया जाता है, तो सरपट मोड से बाहर निकल जाता है। (2)

सरपट दौड़ने की सफलता या विफलता का उपयोग min_gallop को समायोजित करने के लिए किया जाता है। यदि चयनित तत्व उसी सरणी से है जिसने पहले एक तत्व लौटाया था, तो min_gallop एक से कम हो जाता है, इस प्रकार सरपट मोड में वापसी को प्रोत्साहित किया जाता है। अन्यथा, मूल्य एक से बढ़ जाता है, इस प्रकार सरपट मोड में वापसी को हतोत्साहित करता है। यादृच्छिक डेटा के मामले में, min_gallop का मान इतना बड़ा हो जाता है कि सरपट मोड की पुनरावृत्ति कभी नहीं होती है।[13]


अवरोही रन

अवरोही क्रम में क्रमबद्ध डेटा का लाभ उठाने के लिए, टिमसॉर्ट उन्हें मिलने पर कड़ाई से अवरोही रन को उलट देता है और उन्हें रन के ढेर में जोड़ देता है। चूंकि अवरोही रन को बाद में आँख बंद करके उलट दिया जाता है, समान तत्वों वाले रन को छोड़कर एल्गोरिदम की स्थिरता बनी रहती है; यानी, समान तत्वों को उलटा नहीं किया जाएगा।

न्यूनतम रन आकार

टिम्सोर्ट एल्गोरिदम अपने प्रकार को निष्पादित करने के लिए न्यूनतम आकार के आदेशित अनुक्रमों, मिनरन की खोज करता है।

क्योंकि विलय तब सबसे अधिक कुशल होता है जब रनों की संख्या दो की शक्ति के बराबर या उससे थोड़ी कम होती है, और विशेष रूप से कम कुशल होती है जब रनों की संख्या दो की शक्ति से थोड़ी अधिक होती है, यह सुनिश्चित करने का प्रयास करने के लिए टिमसॉर्ट मिनरुन को चुनता है पूर्व स्थिति.[11]

मिनरुन को 32 से 64 समावेशी श्रेणी में से चुना जाता है, जैसे कि डेटा का आकार, मिनरुन द्वारा विभाजित, दो की शक्ति के बराबर या उससे थोड़ा कम होता है। अंतिम एल्गोरिदम सरणी के आकार के छह सबसे महत्वपूर्ण बिट्स लेता है, यदि शेष बिट्स में से कोई भी सेट होता है तो एक जोड़ता है, और उस परिणाम को मिनरुन के रूप में उपयोग करता है। यह एल्गोरिदम सभी सरणियों के लिए काम करता है, जिनमें 64 से छोटी सरणियाँ भी शामिल हैं; 63 या उससे कम आकार की सरणियों के लिए, यह मिनरुन को सरणी आकार के बराबर सेट करता है और टिमसॉर्ट एक सम्मिलन सॉर्ट में कम हो जाता है।[11]


विश्लेषण

सबसे अच्छे, सबसे खराब और औसत मामले में, टिमसॉर्ट लेता है किसी सरणी को क्रमबद्ध करने के लिए तुलनाएँ nतत्व. सबसे अच्छे मामले में, जो तब होता है जब इनपुट पहले से ही सॉर्ट किया गया हो, यह रैखिक समय में चलता है, जिसका अर्थ है कि यह एक अनुकूली सॉर्टिंग एल्गोरिदम है।[3]

ऑब्जेक्ट संदर्भों या पॉइंटर्स को सॉर्ट करने के लिए यह जल्दी से सुलझाएं से बेहतर है क्योंकि इन्हें डेटा तक पहुंचने और तुलना करने के लिए महंगी मेमोरी इनडायरेक्शन की आवश्यकता होती है और क्विकॉर्ट के कैश सुसंगतता लाभ बहुत कम हो जाते हैं।

औपचारिक सत्यापन

2015 में, EU FP7 ENVISAGE प्रोजेक्ट में डच और जर्मन शोधकर्ताओं ने टिमसॉर्ट के मानक कार्यान्वयन में एक बग पाया।[14] इसे 2015 में Python, Java और Android में ठीक किया गया था।

विशेष रूप से, स्टैक्ड रन आकारों पर अपरिवर्तनीय आवश्यक स्टैक के अधिकतम आकार पर एक तंग ऊपरी सीमा सुनिश्चित करते हैं। कार्यान्वयन ने सॉर्ट 2 के लिए पर्याप्त स्टैक पूर्व-आवंटित कियाइनपुट के 64 बाइट्स, और आगे अतिप्रवाह जांच से बचा गया।

हालाँकि, गारंटी के लिए इनवेरिएंट्स को लगातार तीन रनों के प्रत्येक समूह पर लागू करने की आवश्यकता होती है, लेकिन कार्यान्वयन ने इसे केवल शीर्ष तीन के लिए जांचा।[14] जावा सॉफ़्टवेयर चाबी औपचारिक सत्यापन के लिए KeY टूल का उपयोग करते हुए, शोधकर्ताओं ने पाया कि यह जाँच पर्याप्त नहीं है, और वे रन लंबाई (और इनपुट जो उन रन लंबाई उत्पन्न करते हैं) को खोजने में सक्षम थे, जिसके परिणामस्वरूप स्टैक में गहराई से इनवेरिएंट का उल्लंघन हो सकता था। स्टैक के शीर्ष को मर्ज करने के बाद।[15] परिणामस्वरूप, कुछ इनपुट के लिए आवंटित आकार सभी असंबद्ध रन को रखने के लिए पर्याप्त नहीं है। जावा में, यह उन इनपुटों के लिए एक ऐरे-आउट-ऑफ-बाउंड अपवाद उत्पन्न करता है। जावा और एंड्रॉइड v7 में इस अपवाद को ट्रिगर करने वाला सबसे छोटा इनपुट आकार का है 67108864 (226). (पुराने एंड्रॉइड संस्करणों ने पहले ही आकार के कुछ इनपुट के लिए इस अपवाद को ट्रिगर कर दिया है 65536 (216))

अद्यतन सबसे खराब स्थिति विश्लेषण के आधार पर पूर्व-आवंटित स्टैक के आकार को बढ़ाकर जावा कार्यान्वयन को ठीक किया गया था। लेख में औपचारिक तरीकों से यह भी दिखाया गया है कि स्टैक में चार सबसे ऊपरी रन ऊपर दिए गए दो नियमों को पूरा करते हैं या नहीं, इसकी जांच करके इच्छित अपरिवर्तनीय को कैसे स्थापित किया जाए। यह दृष्टिकोण Python द्वारा अपनाया गया था[16] और एंड्रॉइड।

संदर्भ

  1. ↑ Peters, Tim (20 July 2002). "[Python-Dev] Sorting". Python Developers Mailinglist. Retrieved 24 February 2011. [Timsort] also has good aspects: It's stable (items that compare equal retain their relative order, so, e.g., if you sort first on zip code, and a second time on name, people with the same name still appear in order of increasing zip code; this is important in apps that, e.g., refine the results of queries based on user input). ... It has no bad cases (O(N log N) is worst case; N−1 compares is best).
  2. ↑ Auger, Nicolas; Jugé, Vincent; Nicaud, Cyril; Pivoteau, Carine (2018). [DROPS]. doi:10.4230/LIPIcs.ESA.2018.4. ISBN 9783959770811. S2CID 44091254. Retrieved 1 September 2018. TimSort is an intriguing sorting algorithm designed in 2002 for Python, whose worst-case complexity was announced, but not proved until our recent preprint.
  3. ↑ 3.0 3.1 Chandramouli, Badrish; Goldstein, Jonathan (2014). Patience is a Virtue: Revisiting Merge and Sort on Modern Processors. SIGMOD/PODS.
  4. ↑ "[#JDK-6804124] (coll) Replace "modified mergesort" in java.util.Arrays.sort with timsort". JDK Bug System. Retrieved 11 June 2014.
  5. ↑ "Class: java.util.TimSort<T>". Android Gingerbread Documentation. Archived from the original on 16 July 2015. Retrieved 24 February 2011.
  6. ↑ "liboctave/util/oct-sort.cc". Mercurial repository of Octave source code. Lines 23-25 of the initial comment block. Retrieved 18 February 2013. Code stolen in large part from Python's, listobject.c, which itself had no license header. However, thanks to Tim Peters for the parts of the code I ripped-off.
  7. ↑ "Getting things sorted in V8 · V8". v8.dev. Retrieved 21 December 2018.
  8. ↑ "Is sort() stable in Swift 5?". Swift Forums (in English). 4 July 2019. Retrieved 4 July 2019.
  9. ↑ "टुकड़ा - जंग". doc.rust-lang.org. Retrieved 8 December 2022. The current algorithm is an adaptive, iterative merge sort inspired by timsort. It is designed to be very fast in cases where the slice is nearly sorted, or consists of two or more sorted sequences concatenated one after another.
  10. ↑ McIlroy, Peter (January 1993). "Optimistic Sorting and Information Theoretic Complexity". असतत एल्गोरिदम पर चौथे वार्षिक ACM-SIAM संगोष्ठी की कार्यवाही. pp. 467–474. ISBN 0-89871-313-7.
  11. ↑ 11.0 11.1 11.2 "listsort.txt". Python source code. 18 May 2022. Archived from the original on 28 January 2016.
  12. ↑ MacIver, David R. (11 January 2010). "Understanding timsort, Part 1: Adaptive Mergesort". Retrieved 5 December 2015.
  13. ↑ Peters, Tim. "listsort.txt". CPython git repository. Retrieved 5 December 2019.
  14. ↑ 14.0 14.1 de Gouw, Stijn; Rot, Jurriaan; de Boer, Frank S.; Bubel, Richard; Hähnle, Reiner (July 2015). "OpenJDK's Java.utils.Collection.sort() Is Broken: The Good, the Bad and the Worst Case" (PDF). Computer Aided Verification. Lecture Notes in Computer Science. 9206: 273–289. doi:10.1007/978-3-319-21690-4_16. ISBN 978-3-319-21689-8.
  15. ↑ de Gouw, Stijn (24 February 2015). "साबित करना कि एंड्रॉइड, जावा और पायथन का सॉर्टिंग एल्गोरिदम टूटा हुआ है (और इसे ठीक करने का तरीका दिखाएं)". Retrieved 6 May 2017.
  16. ↑ Python Issue Tracker – Issue 23515: Bad logic in timsort's merge_collapse


अग्रिम पठन


बाहरी संबंध

Retrieved from ‘https://www.vigyanwiki.in/index.php?title=टिमसॉर्ट&oldid=226150’