एचपी-एफईएम
एचपी-एफईएम परिमित अवयव विधि (एफईएम) का सामान्य संस्करण होता है | जो खंड अनुसार-बहुपद सन्निकटन के आधार पर आंशिक अंतर समीकरणों का समाधान करने के लिए संख्यात्मक विश्लेषण विधि होती है | और जो वैरिएबल आकार (h) और बहुपद की डिग्री (p) के अवयवों को नियोजित करता है। एचपी-एफईएम की उत्पत्ति बार्ना A सज़ाबो और इवो बाबूस्का के अग्रणी कार्य से हुई है | [1] [2] [3] [4] [5] [6] जिन्होंने इसमें पाया कि परिमित अवयव विधि शीघ्रता से परिवर्तित होती है। और जालक को h-शोधन (अवयवों को लघु भागों में विभाजित करना) होता हैं | इस प्रकार p-शोधन (उनकी बहुपद डिग्री को बढ़ाने) के उपयुक्त संयोजन का उपयोग करके परिष्कृत किया जाता है। यह घातीय अभिसरण अधिकांश अन्य परिमित अवयव विधियों की तुलना में विधि को बहुत आकर्षक बनाता है | जिससे यह सिर्फ बीजगणितीय दर के साथ अभिसरण करता है। एचपी-एफईएम के घातीय अभिसरण का पूर्वानुमान न सिर्फ सैद्धांतिक रूप से किया गया था, किंतु यह अनेक स्वतंत्र शोधकर्ताओं द्वारा भी देखा गया था। [7] [8] [9]
मानक एफईएम से अंतर
एचपी-एफईएम अनेक पहलुओं में मानक (निम्नतम-क्रम) एफईएम से भिन्न होते है।[10]
- उच्च-क्रम आकार कार्यों का चयन उदाहरण आवश्यक: अवयवों में उच्च-डिग्री बहुपद को आकार कार्यों के विभिन्न समुच्चयो का उपयोग करके उत्पन्न किया जा सकता है। ऐसे समुच्चय का चयन कठोरता आव्युह की कंडीशनिंग और उसी स्थान में संपूर्ण समाधान प्रक्रिया को नाटकीय रूप से प्रभावित कर सकता है। इस समस्या को सबसे पहले बाबुस्का एट अल द्वारा प्रलेखित किया गया था।[11]
- स्वचालित एचपी-अनुकूलन: एचपी-एफईएम में, अवयव को अनेक भिन्न-भिन्न विधियों से एचपी-परिष्कृत किया जा सकता है, जैसे: इसे स्पेस में उप-विभाजित किए बिना इसकी बहुपद डिग्री बढ़ाना, या अवयव को ज्यामितीय रूप से उप-विभाजित करना होता हैं | जहां विभिन्न बहुपद डिग्री को उप-अवयवों पर प्रयुक्त किया जा सकता है। और अवयव शोधन प्रत्याशी की संख्या सरलता से दो आयामों में 100 और तीन आयामों में 1000 तक पहुंच जाती है। किसी अवयव में त्रुटि के आकार को सांकेतिक करने वाली संख्या स्वचालित hp-अनुकूलता को निर्देशित करने के लिए पर्याप्त नहीं होती है | यह (मानक एफईएम में अनुकूलता के विपरीत) होती हैं । इस प्रकार यह प्रत्येक अवयव में त्रुटि के आकार के बारे में अधिक सूचना प्राप्त करने के लिए संदर्भ समाधान या विश्लेषणात्मक विचार जैसी अन्य तकनीकों को नियोजित किया जाना चाहिए। [12]
- संयोजन और समाधान सीपीयू समय का अनुपात: मानक एफईएम में, कठोरता आव्युह होता हैं | यह सामान्यतः शीघ्रता से एकत्रित किया जाता है किन्तु यह अधिक विस्तृत होता है। यह सामान्यतः, असतत समस्या के समाधान में कुल कंप्यूटिंग समय का सबसे विस्तृत भाग व्यय होता है। और इसके विपरीत, hp- में एफईएम में कठोरता आव्युह सामान्यतः बहुत लघु होते हैं | किन्तु यह (समान आव्युह आकार के लिए) होता हैं और उनमें एकत्रित मानक एफईएम की तुलना में अधिक समय लगता है। यह मुख्य रूप से संख्यात्मक चतुर्भुज की कम्प्यूटेशनल निवेश के कारण होता है | जिसमें शीघ्र अभिसरण दरों का लाभ उठाने के लिए मानक एफईएम की तुलना में उच्च परिशुद्धता होनी चाहिए | और इसलिए यह उच्च क्रम का होना चाहिए।
- विश्लेषणात्मक चुनौतियाँ: एचपी-एफईएम को सामान्यतः मानक एफईएम की तुलना में विश्लेषणात्मक दृष्टिकोण से समझना अधिक कठिन माना जाता है। जिसके अनुसार यह अनेक तकनीकों से संबंधित होता है, जैसे वृत्ताकार समस्याओं के लिए असतत अधिकतम सिद्धांत (डीएमपी) होता हैं। यह परिणाम बताते हैं कि, सामान्यतः जालक पर कुछ सीमित धारणाओं के साथ, खंड अनुसार-बहुपद एफईएम सन्निकटन अंतर्निहित वृत्ताकार पीडीई के समान अधिकतम सिद्धांतबं का पालन करता है। ऐसे परिणाम बहुत महत्वपूर्ण हैं क्योंकि वे गारंटी देते हैं कि सन्निकटन भौतिक रूप से स्वीकार्य रहता है, जिससे नकारात्मक घनत्व, नकारात्मक एकाग्रता, या नकारात्मक निरपेक्ष तापमान की गणना करने की कोई संभावना नहीं रहती है। डीएमपी निम्नतम-क्रम एफईएम के लिए अधिक अच्छी तरह से समझा जाता है किन्तु दो या दो से अधिक आयामों में एचपी-एफईएम के लिए पूरी तरह से अज्ञात होता है। स्थानिक आयाम में प्रथम डीएमपी वर्तमान में तैयार किया गया था। [13] [14]
- प्रोग्रामिंग चुनौतियाँ: मानक एफईएम कोड की तुलना में hp-एफईएम सॉल्वर को प्रयुक्त करना बहुत कठिन होता है। जिनमें अनेक मुद्दों को दूर करने की आवश्यकता है | यह उनमें सम्मिलित होता हैं (किन्तु यह सिर्फ यहीं तक सीमित नहीं होता हैं) | उच्च-क्रम चतुर्भुज सूत्र, उच्च-क्रम आकार फ़ंक्शन, भौतिक डोमेन में आधार कार्यों के साथ संदर्भ डोमेन पर आकार कार्यों से संबंधित कनेक्टिविटी और अभिविन्यास सूचना आदि होते हैं। [15]
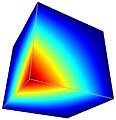
फ़िचेरा समस्या
फिचेरा समस्या (जिसे फिचेरा कॉर्नर समस्या भी कहा जाता है) | यह अनुकूल एफईएम कोड के लिए मानक बेंचमार्क समस्या होती है। कोई इसका उपयोग मानक एफईएम और hp-एफईएम के प्रदर्शन में नाटकीय अंतर दिखाने के लिए कर सकता है। यह समस्या ज्यामिति घन है जिसका कॉर्नर लुप्त होता है।इसमें स्पष्ट समाधान के केंद्र में विलक्षण स्लोप (अनंत तनाव का सादृश्य) होता है। इसमें स्पष्ट समाधान का ज्ञान सन्निकटन त्रुटि की स्पष्ट गणना करना हैं और इस प्रकार यह विभिन्न संख्यात्मक विधियों की तुलना करना संभव बनाता है। उदाहरण के लिए, समस्या को अनुकूली एफईएम के तीन भिन्न-भिन्न संस्करणों का उपयोग करके समाधान किया गया था | जिसमे यह रैखिक अवयवों, द्विघात अवयवों और hp-एफईएम के साथ होता हैं।
अभिसरण ग्राफ स्वतंत्रता की डिग्री (डीओएफ) की संख्या के फ़ंक्शन के रूप में सन्निकटन त्रुटि दिखाते हैं। और डीओएफ अज्ञात मापदंडों को संदर्भित करता है जो सन्निकटन को परिभाषित करने के लिए आवश्यक होते हैं | और डीओएफ की संख्या कठोरता आव्युह के आकार के सामान्य होता है। इसमें रीडर ग्राफ़ में देख सकते हैं कि एचपी-एफईएम का अभिसरण अन्य दोनों विधियों के अभिसरण की तुलना में बहुत शीघ्र होता है। इसमें प्रदर्शन अंतर इतना विस्तृत है कि रैखिक एफईएम पूर्णतया सभी (उचित समय में) अभिसरण नहीं कर सकते है और द्विघात एफईएम को उस स्पष्टता तक पहुंचने के लिए सैकड़ों हजारों या संभवतः लाखों डीओएफ की आवश्यकता होती हैं जो एचपी-एफईएम ने लगभग 17,000 डीओएफ के साथ प्राप्त की थी। यह स्वतंत्रता की अपेक्षाकृत कुछ डिग्री का उपयोग करके बहुत स्पष्ट परिणाम प्राप्त करना एचपी-एफईएम की मुख्य शक्ति होती है।
एचपी-एफईएम की दक्षता
लघु -रेखीय अवयवों की तुलना में विस्तृत उच्च-क्रम वाले अवयवों का उपयोग करके सुचारू कार्यों का अधिक कुशलता से अनुमान लगाया जा सकता है। इसे नीचे दिए गए चित्र में दर्शाया गया है | जहां दो भिन्न-भिन्न जालकों पर शून्य डिरिचलेट सीमा स्थितियों के साथ आयामी पॉइसन समीकरण समाधान किया गया है। यह स्पष्ट समाधान साइन फ़ंक्शन होता है।
- बाएँ: दो रैखिक अवयवों से युक्त जालक हैं।
- दाएँ: द्विघात अवयव से युक्त जालक हैं।
जबकि दोनों स्तिथियों में अज्ञात की संख्या समान है (1 डीओएफ), संबंधित मानदंड में त्रुटियां क्रमशः 0.68 और 0.20 हैं। इसका कारण यह है कि द्विघात सन्निकटन खंड-रेखीय सन्निकटन की तुलना में लगभग 3.5 गुना अधिक कुशल था। जब हम कदम आगे बढ़ते हैं और (a) चार रैखिक अवयवों की तुलना (b) चतुर्थक अवयव (p=4) से करते हैं, तब दोनों भिन्न-भिन्न समस्याओं में तीन डीओएफ होंते हैं | किन्तु चतुर्थक सन्निकटन लगभग 40 गुना अधिक कुशल होता हैं।
इसके विपरीत, लघु निम्न-क्रम वाले अवयव विस्तृत उच्च-क्रम वाले अवयवों की तुलना में लघु मापदंड की विशेषताओं जैसे विलक्षणताओं को उत्तम विधियों से पकड़ सकते हैं। hp-एफईएम इन दो दृष्टिकोणों के इष्टतम संयोजन पर आधारित होता है जो घातांकीय अभिसरण की ओर ले जाता है। ध्यान दें कि यह घातीय अभिसरण त्रुटि की धुरी और स्वतंत्रता की डिग्री में व्यक्त किया गया है। वास्तविक जीवन के अनुप्रयोगों के लिए, हम सामान्यतः स्पष्टता के समान स्तर तक पहुंचने के लिए आवश्यक कम्प्यूटेशनल समय पर विचार करते हैं। इस प्रदर्शन संकेतक के लिए h- और hp-शोधन समान परिणाम प्रदान कर सकते हैं, उदाहरण के लिए [16] (वेब आर्काइव लिंक [17]) पर अंतिम आंकड़ा देखते हैं | जैसे ही h-एफईएम की तुलना में एचपी-एफईएम को प्रोग्राम करना और समानांतर कंप्यूटिंग करना कठिन हो जाता है | एचपी-शोधन की अभिसरण उत्कृष्टता अव्यावहारिक हो सकती है।
एचपी-अनुकूलन
कुछ एफईएम साइटें एचपी-अनुकूलता को h-अनुकूलता (उनकी बहुपद डिग्री को स्थिर रखते हुए स्पेस में अवयवों को विभाजित करता) हैं | और p-अनुकूलता (सिर्फ उनकी बहुपद डिग्री को बढ़ाना) के संयोजन के रूप में वर्णित करती हैं।. यह पूर्ण तरह से स्पष्ट नहीं होती है | क्योंकि hp-अनुकूलता h- और p-अनुकूलता दोनों से अधिक भिन्न होती है क्योंकि किसी अवयव का hp-शोधन अनेक भिन्न-भिन्न विधियों से किया जा सकता है। p-शोधन के अतिरिक्त, अवयव को स्पेस में उप-विभाजित किया जा सकता है (जैसा कि h-अनुकूलता में) हैं, किन्तु उप-अवयवों पर बहुपद डिग्री के लिए अनेक संयोजन होते हैं। यह दाहिनी ओर के चित्र में दर्शाया गया है। उदाहरण के लिए, यदि त्रिकोणीय या चतुर्भुज अवयव को चार उप-अवयवों में विभाजित किया जाता है, जहां बहुपद डिग्री को अधिकतम दो तक भिन्न होने की अनुमति होती है | तब इससे 3^4 = 81 शोधन प्रत्याशी मिलते हैं | इसमें (बहुपद अनिसोट्रोपिक प्रत्याशी पर विचार नहीं किया जाता है)।इस रूप से, हेक्साहेड्रोन को आठ उप-अवयवों में विभाजित करना होता हैं और अधिकतम दो द्वारा उनकी बहुपद डिग्री को परिवर्तित 3^8 = 6,561 शोधन प्रत्याशी प्राप्त करता है। यह प्रति अवयव स्थिर संख्या प्रदान करने वाला मानक एफईएम त्रुटि अनुमान स्वचालित hp-अनुकूलन का मार्गदर्शन करने के लिए पर्याप्त नहीं होता है।
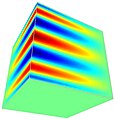
उच्च-क्रम आकार के कार्य
मानक एफईएम में सिर्फ ग्रिड शीर्षों (तथाकथित शीर्ष कार्यों) से जुड़े आकार कार्यों के साथ कार्य करता है। इसके विपरीत, hp-एफईएम का उपयोग करते समय, व्यक्ति एज के कार्यों (अवयव एज से जुड़े), फेस के कार्यों (अवयव फेसों के अनुरूप - केवल 3 डी), और बबल कार्यों (उच्च-क्रम बहुपद जो अवयव सीमाओं पर लुप्त हो जाते हैं) यह इसका भी ध्यान रखता है। निम्नलिखित छवियां इन कार्यों को दिखाती हैं | और यह (एकल अवयव तक सीमित) होते हैं |
ध्यान दें: ये सभी फ़ंक्शन संपूर्ण अवयव इंटीरियर में परिभाषित होते हैं।
ओपन सोर्स एचपी-एफईएम कोड
- डील.II: डील.II परिमित अवयव विधि का उपयोग करके आंशिक अंतर समीकरणों का समाधान करने के लिए निःशुल्क, ओपन-सोर्स लाइब्रेरी है।
- अवधारणाएं: एसएएम, ईटीएच ज्यूरिख (स्विट्जरलैंड) और टीयू बर्लिन (जर्मनी) में के. श्मिट के समूह में अण्डाकार समीकरणों के लिए C/C++ hp-एफईएम/डीजीएफईएम/बीईएम लाइब्रेरी विकसित की गई हैं।
- 2dhp90, 3dhp90: वृत्ताकार समस्याओं और मैक्सवेल के समीकरणों के लिए फोरट्रान कोड आईसीईएस, यूटी ऑस्टिन में एल. डेमकोविज़ द्वारा विकसित।
- पीएचएएमएल: समानांतर पदानुक्रमित अनुकूली बहु-स्तरीय परियोजना हैं। अनुकूली जालक शोधन और मल्टी-ग्रिड समाधान तकनीकों का उपयोग करके वितरित मेमोरी समानांतर कंप्यूटर और मल्टी-कोर कंप्यूटर पर 2 डी वृत्ताकार आंशिक अंतर समीकरणों के संख्यात्मक समाधान के लिए,राष्ट्रीय मानक और प्रौद्योगिकी संस्थान, संयुक्त राज्य अमेरिका में परिमित तत्व सॉफ्टवेयर विकसित किया गया है।
- हर्मीस परियोजना: पीडीई और मल्टीफिजिक्स पीडीई सिस्टम की विशाल विविधता के लिए स्पेस और स्पेस-समय अनुकूली एचपी-एफईएम सॉल्वरों के शीघ्रता से प्रोटोटाइप के लिए C/C++/पायथन लाइब्रेरी, नेवादा विश्वविद्यालय, रेनो (यूएसए), थर्मो-मैकेनिक्स संस्थान, प्राग (चेक गणराज्य) और पिल्सेन (चेक गणराज्य) में वेस्ट बोहेमिया विश्वविद्यालय में एचपी-एफईएम समूह द्वारा विकसित - एग्रोस2डी इंजीनियरिंग सॉफ्टवेयर के शीर्ष पर निर्मित हर्मीस पुस्तकालय हैं |
- पीएचजी: पीएचजी समानांतर अनुकूली परिमित अवयव प्रोग्राम विकसित करने के लिए टूलबॉक्स होता है। यह h-, p- और hp-फेम के लिए उपयुक्त है। पीएचजी वर्तमान में वैज्ञानिक और इंजीनियरिंग कंप्यूटिंग की स्थान प्रमुख प्रयोगशाला हैं | कम्प्यूटेशनल गणित संस्थान और चीनी विज्ञान अकादमी (एलएसईसी, सीएएस, चीन) के वैज्ञानिक/इंजीनियरिंग कंप्यूटिंग संस्थान में सक्रिय विकास पर निर्भर होती है। पीएचजी अनुरूप टेट्राहेड्रल जालक से संबंधित है और संदेश भेजने के लिए अनुकूल स्थानीय जालक शोधन और एमपीआई के लिए द्विभाजन का उपयोग करता है। पीएचजी में ऑब्जेक्ट-ओरिएंटेड डिज़ाइन होता है जो समानांतर विवरण छुपाता है और अमूर्त विधियों से मेष और परिमित अवयव कार्यों पर सामान्य संचालन प्रदान करता है, जिससे उपयोगकर्ताओं को अपने संख्यात्मक एल्गोरिदम पर ध्यान केंद्रित करने की अनुमति मिलती है।
- एमओएफईएम परिमित अवयव विश्लेषण कोड है जो बहु-भौतिकी समस्याओं के समाधान के लिए अनेैतिक रूप से अनुमान के स्तर, जालक शोधन के विभिन्न स्तरों और उच्च-प्रदर्शन कंप्यूटिंग के लिए अनुकूलित किया गया है। इसे L2,H1, H-डीआईवी और H-कर्ल स्थानों के लिए सन्निकटन के विषम क्रम से संबंधित सम्मिश्रों का प्रबंधन करने में सक्षम होने के लिए डिज़ाइन किया गया है।
- स्पार्सेलिज़ार्ड बहु-भौतिकी, hp-अनुकूली, उपयोगकर्ता के अनुकूल, ओपन-सोर्स C++ परिमित अवयव पुस्तकालय है जिसे वर्तमान में टाम्परे विश्वविद्यालय, फिनलैंड में विकसित किया गया है। यह सामान्य स्थैतिक और क्षणिक hp-एफईएम के लिए इच्छानुसार क्रम पदानुक्रमित H1 और H-कर्ल फ़ंक्शन रिक्त स्थान के साथ 3 डी टेट्राहेड्रल और 2 डी त्रिकोण / चतुर्भुज अनुरूप अनुकूली जालक शोधन को जोड़ता है।
वाणिज्यिक एचपी-एफईएम सॉफ्टवेयर
- स्ट्रेसचेक विस्तृत संरचनात्मक विश्लेषण की ओर उन्मुख hp-क्षमताओं वाला सीमित अवयव विश्लेषण उपकरण है।
संदर्भ
- ↑ B. A. Szabó, A. K. Mehta: p-Convergent Finite Element Approximations in Fracture Mechanics, Int. J. Num. Meth. Engng, Volume 12, pp. 551-560, 1978.
- ↑ I. Babuška, B. A. Szabó and I. N. Katz: The p-Version of the Finite Element Method, SIAM J. Numer. Anl., Volume 18, pp. 515-544, 1981.
- ↑ I. Babuška, B. A. Szabó, On the Rates of Convergence of the Finite Element Method, Int. J. Numer. Meth.Engng., Volume 18, pp. 323-341, 1982.
- ↑ I. Babuška: The p- and hp-Versions of the Finite Element Method: the State of the Art, Finite Elements: Theory and Applications, edited by D. L. Dwoyer, M. Y. Hussaini and R. G. Voigt, New York, Springer-Verlag, 1988.
- ↑ B. A. Szabó, I. Babuška: Finite Element Analysis, John Wiley & Sons, ISBN 978-0-471-50273-9, 1991.
- ↑ I. Babuška, B.Q. Guo: The h, p and h-p version of the finite element method: basis theory and applications, Advances in Engineering Software, Volume 15, Issue 3-4, 1992.
- ↑ J.M. Melenk: hp-Finite Element Methods for Singular Perturbations, Springer, 2002
- ↑ C. Schwab: p- and hp- Finite Element Methods: Theory and Applications in Solid and Fluid Mechanics, Oxford University Press, 1998
- ↑ P. Solin: Partial Differential Equations and the Finite Element Method, J. Wiley & Sons, 2005
- ↑ P. Solin, K. Segeth, I. Dolezel: Higher-Order Finite Element Methods, Chapman & Hall/CRC Press, 2003
- ↑ I. Babuska, M. Griebel and J. Pitkaranta, The problem of selecting the shape functions for a p-type finite element, Internat. J. Numer. Methods Engrg. (1989), pp. 1891–1908
- ↑ L. Demkowicz, W. Rachowicz, and Ph. Devloo: A Fully Automatic hp-Adaptivity, Journal of Scientific Computing, 17, Nos 1–3 (2002), 127–155
- ↑ P. Solin, T. Vejchodsky: A Weak Discrete Maximum Principle for hp-FEM, J. Comput. Appl. Math. 209 (2007) 54–65
- ↑ T. Vejchodsky, P. Solin: Discrete Maximum Principle for Higher-Order Finite Elements in 1D, Math. Comput. 76 (2007), 1833–1846
- ↑ L. Demkowicz, J. Kurtz, D. Pardo, W. Rachowicz, M. Paszynski, A. Zdunek: Computing with hp-Adaptive Finite Elements, Chapman & Hall/CRC Press, 2007
- ↑ "Microwave Oven — Hermes Examples Guide".
- ↑ "Microwave Oven — Hermes Examples Guide". hpfem.org. Archived from the original on 7 August 2018. Retrieved 12 January 2022.