स्ट्रिंग-सर्चिंग एल्गोरिदम
कंप्यूटर विज्ञान में, स्ट्रिंग-खोज कलन विधि, कभी-कभी स्ट्रिंग-मिलान कलन-विधि के रूप में जाने जाते हैं, स्ट्रिंग कलन-विधि की एक महत्वपूर्ण श्रेणी हैं, जो एक या एक से अधिक स्ट्रिंग को एक बड़े स्ट्रिंग या टेक्स्ट में ढूंढने का प्रयास करते हैं।
एक उपस्थित उदाहरण स्ट्रिंग खोज का है जब पैटर्न और खोजी जाने वाली टेक्स्ट Σ के तत्वों के सरणी होते हैं। Σ किसी मानवीय भाषा का वर्णमाला हो सकता है, जैसे अक्षर A से Z तक, और अन्य अनुप्रयोग जैव सूचना विज्ञान में एक बाइनरी वर्णमाला (Σ = {0,1}) या एक डीएनए वर्णमाला (Σ = {A,C,G,T}) का उपयोग कर सकते हैं।
व्यावहारिकता में, संभावित स्ट्रिंग-खोज कलन-विधि का नियम स्ट्रिंग कूटलेखन पर प्रभावित हो सकता है। विशेष रूप से, यदि किसी चरित्र की चरित्रिता विस्तार सहित प्रयोग हो रही है, तो N वें वर्ण को खोजना धीमा हो सकता है, प्रायः N के समान समय की आवश्यकता हो सकती है। इससे कुछ खोज कलन-विधि को बहुत ही धीमा बना सकता है। एक बहुत सारे संभावित समाधान में से एक स्ट्रिंग कोड यूनिट के लिए खोज करना है, परंतु ऐसा करने पर गलत मिलान हो सकते हैं जब तक कि कूटलेखन से बचने के लिए विशेष रूप से आरेखित नहीं की गई है।
अवलोकन
स्ट्रिंग खोज का सबसे मूल स्थिति एक स्ट्रिंग और एक स्ट्रिंग के बीच का होता है, जिसे कभी-कभी हेस्टेक कहा जाता है और जिसे कभी-कभी नीडल कहा जाता है। लक्ष्य होता है कि हेस्टेक में नीडल के एक या एक से अधिक प्रतिस्थानों का पता लगाया जाए। उदाहरण के लिए, किसी व्यक्ति की हिंदी भाषा में "तो" की खोज की जा सकती है।
Some books are to be tasted, others to be swallowed, and some few to be chewed and digested
किसी को "to" की पहली प्राप्ति, जो चौथा शब्द है, मांग सकते हैं; या सभी प्राप्तियों को, जिनमें 3 हैं; या अंतिम, जो अंत से पांचवा शब्द है, मांग सकते हैं।
सामान्यतः, इसके साथ-साथ विभिन्न प्रतिबंध भी लगाए जाते हैं। उदाहरण के लिए, कोई व्यक्ति "नीडल" के सिर्फ उन प्रतिस्थानों का मेल करना चाह सकता है जहां वह एक पूर्ण शब्द के रूप में होती है प्रायः उसे उनके दोनों ओर संबंधित अक्षरों के आसपास कोई अन्य अक्षर नहीं होने के रूप में परिभाषित किया गया हो। इस स्थिति में, उपरोक्त उदाहरण में "hew" or "low" की खोज विफल होनी चाहिए, यद्यपि वास्तविक तत्व उपस्थित हैं।
एक और सामान्य उदाहरण "मानकीकरण" से जुड़ा होता है। कई उद्देश्यों के लिए, "होना" जैसी वाक्यांश की खोज को "तक" और "होना" के बीच किसी अन्य वस्तु के संबंध में सफल होना चाहिए, भले ही "तक" और "होना" के बीच कुछ और अवरुद्ध हो।:
- एक से अधिक स्थान
- टैग, गैर-टूटने वाले रिक्त स्थान, लाइन टोडने आदि जैसे अन्य "व्हाट्सएप" वर्ण भी हो सकते हैं।
- कम सामान्यतः, एक हाइफ़न या नरम हाइफ़न
- संरचित टेक्स्टों में, मार्कअप भाषा या यहां तक कि मनमाने ढंग से बड़ी लेकिन पैरेंटेटिकल वस्तुए जैसे फ़ुटनोट्स, सूची-संख्याएं या अन्य मार्कर, अंतर्निहित छवियां इत्यादि।
कई प्रतीक प्रणालियों में ऐसे वर्ण सम्मिलित होते हैं जो पर्यायवाची होते हैं :
- लैटिन-आधारित वर्णमाला लोअर-केस को अपर-केस से अलग करती है, लेकिन कई उद्देश्यों के लिए स्ट्रिंग खोज से इस अंतर को अनदेखा करने की उम्मीद की जाती है।
- कई भाषाओं में मुद्रण संयुक्ताक्षर सम्मिलित हैं, जहां एक मिश्रित वर्ण दो या दो से अधिक अन्य वर्णों के बराबर होता है।
- कई लेखन प्रणालियों में उच्चारण या स्वर संकेत जैसे विशेषक चिह्न सम्मिलित होते हैं, जो उनके उपयोग में भिन्न हो सकते हैं, या मिलान में अलग-अलग महत्व के हो सकते हैं।
- डीएनए अनुक्रमों में गैर-कोडिंग खंड सम्मिलित हो सकते हैं जिन्हें कुछ उद्देश्यों के लिए अनदेखा किया जा सकता है, या बहुरूपताएं जो एन्कोडेड प्रोटीन में कोई बदलाव नहीं लाती हैं, जो कुछ अन्य उद्देश्यों के लिए वास्तविक अंतर के रूप में नहीं गिना जा सकता है।
- कुछ भाषाओं में ऐसे नियम होते हैं जहां शब्दों के आरंभ, मध्य या अंत में एक अलग वर्ण या वर्ण के रूप का उपयोग किया जाना चाहिए।
अंततः, प्राकृतिक भाषा का प्रतिनिधित्व करने वाली स्ट्रिंग के लिए, भाषा के पहलू स्वयं सम्मिलित हो जाते हैं। उदाहरण के लिए, कोई व्यक्ति वैकल्पिक वर्तनी, उपसर्ग या प्रत्यय आदि होने के अतिरिक्त किसी शब्द की सभी घटनाओं को खोज जा सकता है।
खोज का एक और अधिक जटिल प्रकार नियमित अभिव्यक्ति खोज है, जहां उपयोगकर्ता वर्णों या अन्य प्रतीकों का एक पैटर्न बनाता है, और पैटर्न के किसी भी मिलान से खोज पूरी होनी चाहिए। उदाहरण के लिए, अमेरिकी अंग्रेजी शब्द कलर और ब्रिटिश समकक्ष कलर दोनों को पकड़ने के लिए, दो अलग-अलग शाब्दिक तारों की खोज करने के अतिरिक्त, कोई नियमित अभिव्यक्ति का उपयोग कर सकता है जैसे:
colou?r
जहां ? परंपरागत रूप से पूर्ववर्ती वर्ण (u) को वैकल्पिक बनाता है।
यह आलेख मुख्य रूप से सरल प्रकार की स्ट्रिंग खोज के लिए कलन-विधि पर चर्चा करता है।
जैव सूचना विज्ञान और जीनोमिक्स के क्षेत्र में प्रस्तुत की गई एक समान समस्या अधिकतम सटीक मिलान (एमईएम) है।[1] दो स्ट्रिंग्स को देखते हुए, एमईएम सामान्य उपस्ट्रिंग हैं जिन्हें असंगत उत्पन्न किए बिना बाएं या दाएं नहीं बढ़ाया जा सकता है।[2]
खोज कलन-विधि के उदाहरण
सरल स्ट्रिंग खोज
एक सरल और अप्रभावी विधि जिसके द्वारा देखा जा सकता है कि एक स्ट्रिंग किसी अन्य स्ट्रिंग में कहां होती है, सबसे पहले, हम देखते हैं कि क्या हेस्टेक के पहले अक्षर से पैटर्न की एक प्रतिलिपि है; यदि नहीं, तो हम देखते हैं कि क्या हेस्टेक के दूसरे अक्षर से पैटर्न की एक प्रतिलिपि है, और ऐसा आगे भी होता है। सामान्य विधि में, हमें गलत स्थान के प्रत्येक अक्षर को देखने के लिए केवल एक या दो अक्षर देखने की जरूरत होती है जिससे हम यह देख सकें कि यह गलत स्थान है, इसलिए औसत स्थितियों में, इसमें O(n + m) चरण लगते हैं, जहां n हेस्टेक की लंबाई है और m पैटर्न की लंबाई है; लेकिन सबसे खराब मामले में, "aaaaaaaaab" जैसे स्ट्रिंग में "aaaab" जैसे स्ट्रिंग की खोज करने में O(nm) समय लगता है।
परिमित-अवस्था-ऑटोमेटन-आधारित खोज
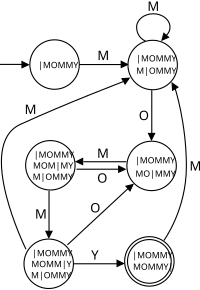
इस दृष्टिकोण में, पीछे जाने को दूर किया जाता है द्वारा एक निर्दिष्ट सीमित स्वतंत्र ऑटोमेटन का निर्माण करके जो संग्रहीत खोज स्ट्रिंग को मान्य करता है। इनका निर्माण करना खर्चीला होता है सामान्यतः यह पावरसेट निर्माण का उपयोग करके बनाया जाता है - लेकिन उपयोग करने में बहुत तेज होते हैं। उदाहरण के लिए, दिए गए डीएफए में "एमओएमएमवाई" शब्द को मान्य करता है। यह दृष्टिकोण सामान्यतः व्यावहारिक रूप से सामान्य किया जाता है जिससे विचाराधीन नियमित अभिव्यक्तियों के लिए खोज की जा सके।
स्टब्स
नथ-मॉरिस-प्रैट एक डीएफए की गणना करता है जो प्रत्यय के रूप में खोज करने के लिए स्ट्रिंग के साथ इनपुट को पहचानता है, बॉयर-मूर सुई के अंत से खोज प्रारम्भ करता है, इसलिए यह सामान्यतः प्रत्येक चरण में पूरी सुई-लंबाई से आगे बढ़ सकता है। बाएजा-येट्स कलन-विधि में पिछले j अक्षर ध्वनि खोज स्ट्रिंग के उपसर्ग के रूप में हैं या नहीं, यह जांच रखता है, और इसलिए यह सुधारणात्मक स्ट्रिंग खोज के लिए अनुकूल है। बिटाप कलन-विधि बाएजा-येट्स के दृष्टिकोण का एक अनुप्रयोग है।
सूचकांक विधियाँ
तेज़ खोजकलन विधि प्राकृतिक भाषा में पूर्वप्रसंस्कृत करते हैं। एक उपस्ट्रिंग सूचकांक का निर्माण करने के बाद, जैसे कि सफिक्स ट्री या सफिक्स एरे, पैटर्न की प्रतिस्थान तेजी से मिल सकते हैं। एक उदाहरण के रूप में, एक सफिक्स ट्री समय में निर्मित की जा सकती है प्रतिस्थान समय में मिल सकते हैं, यहां इस परिकल्पना के तहत कि अक्षरमाला का एक स्थायी आकार है और उप स्ट्रिंग ट्री के सभी आंतरिक नोड़ जानते हैं कि उनके नीचे कौन से पत्ते हैं। इसको उपसर्ग ट्री के रूट से एक डीएफएस कलन-विधि चलाकर प्राप्त किया जा सकता है।
अन्य प्रकार
कुछ खोज विधियाँ, उदाहरण के लिए ट्रिग्राम खोज , का उद्देश्य मिलान/गैर-मिलान के अतिरिक्त खोज स्ट्रिंग और टेक्स्ट के बीच निकटता स्कोर खोजता है। इन्हें कभी-कभी अनुमानित स्ट्रिंग मिलान कहा जाता है|
खोज कलन-विधि का वर्गीकरण
विभिन्न पैटर्न द्वारा वर्गीकरण
विभिन्न कलन विधि को प्रत्येक उपयोग किए जाने वाले पैटर्न की संख्या के आधार पर वर्गीकृत किया जा सकता है।
एकल-पैटर्न कलन-विधि
इस प्रकार के संकलन में, m पैटर्न की लंबाई है, n खोजने योग्य टेक्स्ट की लंबाई है, और k = |Σ| अक्षरमाला का आकार है।
| कलन विधि | प्रीप्रोसेसिंग समय | मिलान समय | स्पेस |
|---|---|---|---|
| अनुभवहीन कलन विधि | none | Θ(mn) | none |
| राबिन-कार्प | Θ(m) | Θ(n) in average, O(mn) at worst |
O(1) |
| नुथ-मॉरिस-प्रैट | Θ(m) | Θ(n) | Θ(m) |
| बॉयर-मूर | Θ(m + k) | Ω(n/m) at best, O(mn) at worst |
Θ(k) |
| दो विधि से कलन विधि [3][1] | Θ(m) | O(n) | O(log(m)) |
| पिछड़ा गैर-नियतात्मक डीएडब्ल्यूजी मिलान | O(m) | Ω(n/m) at best, O(mn) at worst |
|
| बैकवर्ड ओरेकल मिलान (बीओएम) | O(m) | O(mn) |
- 1.संक्षेप में,कलन विधि विश्लेषण में व्यास्तिक काल को सामान्यतः O (बड़ा ओ), Ω (ओमेगा) और Θ (थीटा) नोटेशन का प्रयोग करके व्यक्त किया जाता है।
- 2.^ यह O(m + n) समय में काम करता है, जहां m पैटर्न की लंबाई है और n खोजने योग्य टेक्स्ट की लंबाई है। इसलिए,अधिकांश स्थितियों में यह तेजी से काम करता है
- 3.^ यह सुनिश्चित करने के लिए कि लगभग सही स्ट्रिंग मैचिंग को हैंडल किया जा सके और नियमित भाषाओं के रूप में प्रतिष्ठित विभिन्न पैटर्नों के सेट को हैंडल किया जा सके, इसे विस्तारित किया जा सकता है।
यर-मोर स्ट्रिंग-खोज कलन विधि वास्तविक स्ट्रिंग-खोज साहित्य में मानक मानदण्ड माना जाता है। यह कार्यात्मकता और कुशल स्ट्रिंग-खोज कलन विधि में उच्च स्तर प्राप्त करने के लिए जाना जाता है।[4]
पैटर्न के एक सीमित सेट का उपयोग करने वाले कलन-विधि
निम्नलिखित संकलन में, M सबसे लंबे पैटर्न की लंबाई है, m उनकी कुल लंबाई है, n खोजने योग्य टेक्स्ट की लंबाई है, और o प्राप्तियों की संख्या है।
| कलनविधि | विस्तार | प्रीप्रोसेसिंग समय | मिलान समय | स्पेस |
|---|---|---|---|---|
| अहो-कोरासिक | नुथ-मॉरिस-प्रैट | Θ(m) | Θ(n + o) | Θ(m) |
| कॉमेंट्ज़-वाल्टर | बोयर-मूर | Θ(m) | Θ(M * n) worst case sublinear in average[5] |
Θ(m) |
| सेट-बीओएम | पिछड़ा ओरेकल मिलान |
अनंत संख्या में पैटर्न का उपयोग करने वाले कलन-विधि
स्वाभाविक रूप से, इस मामले में पैटर्न को अंतिम रूप से गिना नहीं जा सकता है। इन्हें सामान्यतः नियमित व्याकरण या नियमित अभिव्यक्ति द्वारा दर्शाया जाता है।
पूर्वप्रसंस्करण प्रोग्राम के उपयोग द्वारा वर्गीकरण
अन्य वर्गीकरण दृष्टिकोण भी संभव हैं। सबसे सामान्य उपयोग पूर्वसंस्कारण को मुख्य मापदंड के रूप में होता है।
| टेक्स्ट पूर्वसंसाधित नहीं है | टेक्स्ट पूर्वसंसाधित | |
|---|---|---|
| पैटर्न पूर्व-संसाधित नहीं हैं | प्राथमिक कलन विधि | सूचकांक विधियाँ |
| पैटर्न पूर्व-संसाधित | खोज इंजनों का निर्माण किया | हस्ताक्षर के नियम |
मिलान रणनीतियों द्वारा वर्गीकरण
एक अन्य कलन-विधि को उनकी मिलान रणनीति के आधार पर वर्गीकृत करता है:[7]
- पहले उपसर्ग का मिलान करें (नुथ-मॉरिस-प्रैट, शिफ्ट-एंड, अहो-कोरासिक)
- पहले प्रत्यय का मिलान करें (बॉयर-मूर और वेरिएंट, कमेंट्ज़-वाल्टर)
- सबसे पहले सर्वोत्तम कारक का मिलान करें (बीएनडीएम, बीओएम, सेट-बीओएम)
- अन्य रणनीति (अनुभवहीन, राबिन-कार्प)
यह भी देखें
- अनुक्रम संरेखण
- ग्राफ़ मिलान
- पैटर्न मिलान
- संपीड़ित पैटर्न मिलान
- वाइल्डकार्ड का मिलान
- पूरा टेक्स्ट खोज ें
संदर्भ
- ↑ Kurtz, Stefan; Phillippy, Adam; Delcher, Arthur L; Smoot, Michael; Shumway, Martin; Antonescu, Corina; Salzberg, Steven L (2004). "बड़े जीनोम की तुलना के लिए बहुमुखी और खुला सॉफ्टवेयर". Genome Biology. 5 (2): R12. doi:10.1186/gb-2004-5-2-r12. ISSN 1465-6906. PMC 395750. PMID 14759262.
- ↑ Khan, Zia; Bloom, Joshua S.; Kruglyak, Leonid; Singh, Mona (2009-07-01). "विरल प्रत्यय सरणियों का उपयोग करके बड़े अनुक्रम डेटासेट में अधिकतम सटीक मिलान खोजने के लिए एक व्यावहारिक एल्गोरिदम". Bioinformatics. 25 (13): 1609–1616. doi:10.1093/bioinformatics/btp275. PMC 2732316. PMID 19389736.
- ↑ Crochemore, Maxime; Perrin, Dominique (1 July 1991). "Two-way string-matching" (PDF). Journal of the ACM. 38 (3): 650–674. doi:10.1145/116825.116845. S2CID 15055316. Archived (PDF) from the original on 24 November 2021. Retrieved 5 April 2019.
- ↑ Hume; Sunday (1991). "तेज़ स्ट्रिंग खोज". Software: Practice and Experience. 21 (11): 1221–1248. doi:10.1002/spe.4380211105. S2CID 5902579. Archived from the original on 2022-05-10. Retrieved 2019-11-29.
- ↑ Commentz-Walter, Beate (1979). A String Matching Algorithm Fast on the Average (PDF). International Colloquium on Automata, Languages and Programming. LNCS. Vol. 71. Graz, Austria: Springer. pp. 118–132. doi:10.1007/3-540-09510-1_10. ISBN 3-540-09510-1. Archived from the original (PDF) on 2017-10-10.
- ↑ Melichar, Borivoj, Jan Holub, and J. Polcar. Text Searching Algorithms. Volume I: Forward String Matching. Vol. 1. 2 vols., 2005. http://stringology.org/athens/TextSearchingAlgorithms/ Archived 2016-03-04 at the Wayback Machine.
- ↑ Gonzalo Navarro; Mathieu Raffinot (2008), Flexible Pattern Matching Strings: Practical On-Line Search Algorithms for Texts and Biological Sequences, ISBN 978-0-521-03993-2
- R. S. Boyer and J. S. Moore, A fast string searching algorithm, Carom. ACM 20, (10), 262–272(1977).
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Third Edition. MIT Press and McGraw-Hill, 2009. ISBN 0-262-03293-7. Chapter 32: String Matching, pp. 985–1013.
बाहरी संबंध
- Huge list of pattern matching links Last updated: 12/27/2008 20:18:38
- Large (maintained) list of string-matching algorithms
- NIST list of string-matching algorithms
- StringSearch – high-performance pattern matching algorithms in Java – Implementations of many String-Matching-Algorithms in Java (BNDM, Boyer-Moore-Horspool, Boyer-Moore-Horspool-Raita, Shift-Or)
- StringsAndChars – Implementations of many String-Matching-Algorithms (for single and multiple patterns) in Java
- Exact String Matching Algorithms — Animation in Java, Detailed description and C implementation of many algorithms.
- (PDF) Improved Single and Multiple Approximate String Matching
- Kalign2: high-performance multiple alignment of protein and nucleotide sequences allowing external features
- NyoTengu – high-performance pattern matching algorithm in C – Implementations of Vector and Scalar String-Matching-Algorithms in C