यांत्रिक कैलकुलेटर

From Vigyanwiki
Revision as of 07:45, 8 August 2023 by Indicwiki (talk | contribs) (24 revisions imported from alpha:यांत्रिक_कैलकुलेटर)
1851 के पश्चात से कार्यालय में विभिन्न डेस्कटॉप मैकेनिकल कैलकुलेटर का उपयोग किया गया। प्रत्येक का यूजर अंतरापृष्ठ भिन्न है। यह चित्र ऊपर बाईं ओर से दक्षिणावर्त दिखाता है: अरिथमोमीटर, कंप्टमीटर, डाल्टन ऐडिंग मशीन, सुंदरस्ट्रैंड और ओडनेर अरिथमोमीटर

यांत्रिक कैलकुलेटर, या गणना करने वाली मशीन, ऐसा यांत्रिक उपकरण है जिसका उपयोग अंकगणित के मूल संचालन को स्वचालित रूप से करने के लिए किया जाता है, या (ऐतिहासिक रूप से) एनालॉग कंप्यूटर या स्लाइड नियम जैसे सिमुलेशन के लिए किया जाता है। अधिकांश यांत्रिक कैलकुलेटर आकार में छोटे डेस्कटॉप कंप्यूटर के तुलनीय थे और इलेक्ट्रॉनिक कैलकुलेटर और डिजिटल कम्प्यूटर के आगमन से अप्रचलित हो गए हैं।

1623 में विल्हेम स्किकार्ड के जीवित नोटों से ज्ञात होता है कि उन्होंने मशीनीकृत गणना के आधुनिक प्रयासों को डिजाइन और निर्मित किया था। उनकी मशीन प्रौद्योगिकियों के दो सेटों से बनी थी: प्रथम नेपियर की हड्डियों से निर्मित अबेकस, जिसका वर्णन छह वर्ष पूर्व 1617 में प्रथम बार गुणा और भाग को सरल बनाने के लिए किया गया था, और यांत्रिक भाग के लिए, इसमें जोड़ और घटाव करने के लिए डायल किया गया पेडोमीटर था। शेष नोटों के अध्ययन से ज्ञात होता है कि मशीन जो एक ही डायल पर कुछ प्रविष्टियों के पश्चात जाम हो जाती है,[1] और यदि कैरी को कुछ अंकों (जैसे 1 को 999 में जोड़ना) पर प्रचारित करना पड़े तो यह क्षतिग्रस्त हो सकती है।[2] स्किकार्ड ने 1624 में अपनी परियोजना को त्याग दिया और 11 वर्ष पश्चात 1635 में अपनी मृत्यु तक इसका पुनः उल्लेख नहीं किया।

स्किकार्ड के कथित रूप से विफल प्रयास के दो दशक पश्चात, 1642 में, ब्लेस पास्कल ने यांत्रिक कैलकुलेटर के अपने आविष्कार के साथ निर्णायक रूप से इन विशेष समस्याओं का समाधान किया।[3] रूएन में कर संग्राहक के रूप में अपने पिता के कार्य में सम्मिलित होने के पश्चात, पास्कल ने अधिक मात्रा में आवश्यक कठिन अंकगणित में सहायता करने के लिए कैलकुलेटर डिज़ाइन किया;[4] इसे पास्कल का कैलकुलेटर या पास्कलिन कहा जाता था।[5]

1672 में गॉटफ्रीड लेबनीज़ ने स्टेप्ड रेकनर नामक पूर्ण रूप से नई मशीन डिजाइन करना प्रारम्भ किया। इसने स्टेप्ड ड्रम का उपयोग किया गया था, जिसे उनके द्वारा निर्मित किया गया था और उनके नाम पर लेबनीज़ व्हील रखा गया था, यह प्रथम दो-गति वाला कैलकुलेटर था, कर्सर का उपयोग करने वाला प्रथम (प्रथम ऑपरेंड की मेमोरी बनाने वाला) और चलने योग्य गाड़ी रखने वाला था। लेबनीज़ ने दो स्टेप्ड रेकोनर एक 1694 में और दूसरा 1706 में निर्मित किये थे।[6] लेबनीज़ व्हील का उपयोग 200 वर्षों तक कई गणना मशीनों में किया गया था, और 1970 के दशक में कर्टा हैंड कैलकुलेटर के साथ, 1970 के दशक के मध्य में इलेक्ट्रॉनिक कैलकुलेटर के आगमन तक किया गया था। लेबनीज़ पिनव्हील कैलकुलेटर के विचार को बढ़ावा देने वाले प्रथम व्यक्ति भी थे।[7]

थॉमस का अंकगणितमापी, प्रथम व्यावसायिक रूप से सफल मशीन, दो सौ वर्ष पश्चात 1851 में निर्मित की गई थी; यह प्रथम यांत्रिक कैलकुलेटर था जो इतना दृढ़ं और विश्वसनीय था कि इसे कार्यालय के वातावरण में प्रतिदिन उपयोग किया जा सकता था। 1890 में अधिक सफल ओडनेर एरिथमोमीटर के औद्योगिक उत्पादन तक चालीस वर्षों तक व्यापार के लिए उपलब्ध यांत्रिक कैलकुलेटर का एकमात्र प्रकार था।[8]

1887 में प्रस्तुत किया गया कॉम्पटोमीटर, कीबोर्ड का उपयोग करने वाली प्रथम मशीन थी जिसमें प्रत्येक अंक के लिए नौ कुंजी (1 से 9 तक) के कॉलम सम्मिलित थे। 1902 में निर्मित डाल्टन ऐडिंग मशीन, 10 कुंजी कीबोर्ड वाली प्रथम मशीन थी।[9] 1901 से कुछ यांत्रिक कैलकुलेटरों पर विद्युत मोटरों का उपयोग किया जाने लगा था।[10] 1961 में, कॉम्पटोमीटर प्रकार की मशीन, सुमलॉक कॉम्पटोमीटर लिमिटेड एएनआईटीए एमके VII, ऑल-इलेक्ट्रॉनिक कैलकुलेटर इंजन प्राप्त करने वाला प्रथम डेस्कटॉप मैकेनिकल कैलकुलेटर बन गया, जिसने इन दोनों उद्योगों के मध्य लिंक बनाता है और इसके पतन के प्रारम्भ को चिह्नित करता है। 1970 के दशक के मध्य में यांत्रिक कैलकुलेटर का उत्पादन विवृत हो गया और ऐसा उद्योग विवृत हो गया जो 120 वर्षों तक चला था।

चार्ल्स बैबेज ने दो नए प्रकार के यांत्रिक कैलकुलेटर प्रस्तुत किए, जो इतने बड़े थे कि उन्हें संचालित करने के लिए भाप इंजन की शक्ति की आवश्यकता होती थी, और जो उनके जीवनकाल में निर्मित होने के लिए अधिक परिष्कृत थे। प्रथम स्वचालित यांत्रिक कैलकुलेटर था, उसका अंतर इंजन, जो स्वचालित रूप से गणितीय सारणीओं की गणना और प्रिंट कर सकता था। 1855 में, जॉर्ज शुट्ज़ अपने अंतर इंजन के छोटे और सरल मॉडल के निर्माण में सफल होने वाले अल्प मात्रित डिजाइनरों में से प्रथम बन गए थे।[11] दूसरा प्रोग्रामयोग्य यांत्रिक कैलकुलेटर था, उनका विश्लेषणात्मक इंजन, जिसे बैबेज ने 1834 में डिजाइन करना प्रारम्भ किया था; दो वर्ष से भी अल्प समय में उन्होंने आधुनिक कंप्यूटर की कई मुख्य विशेषताओं को रेखांकित किया था। जैक्वार्ड लूम से प्राप्त पंच कार्ड प्रणाली को अपनाना महत्वपूर्ण कदम था[12] जिससे इसे असीमित रूप से प्रोग्राम करने योग्य निर्मित किया जा सकता था।[13] 1937 में, हावर्ड ऐकेन ने आईबीएम को विश्लेषणात्मक इंजन की वास्तुकला के आधार पर विशेष प्रकार की प्रथम मशीन एएससीसी/मार्क I के डिजाइन करने और निर्माण के लिए अनुकूल किया गया था;[14] जब मशीन प्रस्तुत हो गई तो कुछ लोगों ने इसे बैबेज के सपने के सत्य होने के रूप में प्रशंसा की थी।[15]

प्राचीन इतिहास

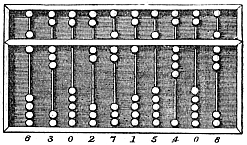
चीनी एसयू काला बाजार (तस्वीर में दर्शाई गई संख्या 6,302,715,408 है)
Further information: अंकगणित and अबेकस

अंकगणितीय गणनाओं में समय और मानसिक प्रयास को अल्प करने और त्रुटि के प्रति मानवीय दायित्व को समाप्त करने की इच्छा संभवतः अंकगणित के विज्ञान जितनी ही प्राचीन है। इस इच्छा ने गणना के लिए विभिन्न प्रकार की सहायता के डिजाइन और निर्माण को प्रेरित किया है, जिसका प्रारम्भ छोटी वस्तुओं के समूहों से हुई, जैसे कि कंकड़, पूर्व कोमल रूप से उपयोग किए जाते थे, अंत में शासित बोर्डों पर काउंटर के रूप में, और पश्चात में अभी भी तारों पर लगे मोतियों के रूप में उपयोग किए जाते थे। फ्रेम, जैसे अबेकस में उपयोग किए जाते थे। इस उपकरण का आविष्कार संभवतः सेमेटिक जातियों द्वारा किया गया था और अंत में इसे भारत में अपनाया गया, जहां से यह पश्चिम की ओर पूरे यूरोप और पूर्व की ओर चीन और जापान तक विस्तारित हो गया था।
अबेकस के विकास के पश्चात, 1617 में जॉन नेपियर द्वारा अपनी नंबरिंग छड़ें, या नेपियर की हड्डियां प्रस्तुत करने तक कोई और प्रगति नहीं हुई। हड्डियों के विभिन्न रूप सामने आए, कुछ यांत्रिक गणना के प्रारम्भ के निकट पहुंच गए, किन्तु ऐसा नहीं था 1642 तक ब्लेज़ पास्कल ने हमें उस अर्थ में प्रथम यांत्रिक गणना मशीन दी, जिस अर्थ में यह शब्द वर्तमान में प्रयोग किया जाता है।

— हॉवर्ड ऐकेन, प्रस्तावित स्वचालित गणना मशीन, 1937 में आईबीएम को प्रस्तुत की गई थी।
Further information: पास्कल का कैलकुलेटर प्रीकर्सर्स

यांत्रिक कैलकुलेटर के अन्य अग्रदूतों की छोटी सूची में यांत्रिक एनालॉग कंप्यूटरों का समूह सम्मिलित होना चाहिए, जो एक बार सेट हो जाने पर, केवल उनके एक्चुएटर्स (क्रैंक हैंडल, भार, व्हील, पानी ...) की निरंतर और बार-बार कार्रवाई द्वारा संशोधित होते हैं। सामान्य युग से पूर्व, ओडोमीटर और एंटीकाइथेरा प्रणाली थे, प्रतीत होता है कि आउट-ऑफ-द-प्लेस आर्टिफैक्ट, अद्वितीय, गियर वाली खगोलीय घड़ी थी, सहस्राब्दी से भी अधिक समय पश्चात में प्रारंभिक यांत्रिक घड़ियों, गियर वाली एस्ट्रॉलैब और 15 वीं शताब्दी में पेडोमीटर द्वारा पीछा किया गया। ये सभी मशीनें टूटेड गियर्स से बनी थीं जो किसी प्रकार के कैरी मैकेनिज्म से जुड़ी थीं। ये मशीनें सदैव यांत्रिक कैलकुलेटर के विपरीत समान प्रारंभिक सेटिंग्स के लिए समान परिणाम उत्पन्न करती हैं, जहां सभी पहिए स्वप्रणाली होते हैं किन्तु अंकगणित के नियमों द्वारा साथ जुड़े होते हैं।

17वीं सदी

अवलोकन

17 वीं शताब्दी ने यांत्रिक कैलकुलेटर के इतिहास का प्रारम्भ हुआ, क्योंकि 1642 में पास्कल के कैलकुलेटर सहित इसकी प्रथम मशीनों का आविष्कार हुआ था।[4][16] ब्लेज पास्कल ने ऐसी मशीन का आविष्कार किया था जिसे उन्होंने संगणना करने में सक्षम होने के रूप में प्रस्तुत किया था जिसे प्रथम केवल मानवीय रूप से संभव माना जाता था।[17]

विशेष प्रकार से, पास्कल का आविष्कार समय से पूर्व हुआ था, क्योंकि उनके समय में यांत्रिक कलाएं इतनी उन्नत नहीं थीं कि उनकी मशीन को उत्तम मूल्य पर, उचित लंबे समय तक उपयोग के लिए आवश्यकत्रुटिहीनता और शक्ति के साथ बनाया जा सके। यह कठिनाई उन्नीसवीं शताब्दी तक दूर नहीं हुई थी, उस समय तक पास्कल द्वारा मानी जाने वाली गणनाओं की तुलना में अधिक जटिल कई प्रकार की गणनाओं की आवश्यकता के कारण आविष्कार के लिए नई प्रेरणा दी गई थी।

— एस चैपमैन, पास्कल टेरसेंटेनरी उत्सव, लंदन, (1942)[18]

17वीं शताब्दी में अंकगणितीय गणनाओं में सहायता के लिए नेपियर की हड्डियां, लघुगणकीय सारणीएँ और स्लाइड नियम जैसे कुछ अधिक शक्तिशाली उपकरणों का आविष्कार भी हुआ था, जो वैज्ञानिकों द्वारा गुणा और विभाजन में उनके उपयोग में 19वीं शताब्दी के मध्य में एरिथमोमीटर के उत्पादन के प्रस्तावित होने तक सरलता के लिए शासन करते थे और यांत्रिक के उपयोग और विकास को बाधित करते थे।[19]

पास्कल के चार कैलकुलेटर और 1725 में लेपाइन द्वारा निर्मित मशीन,[20] कला और शिल्प संग्रहालय

यांत्रिक कैलकुलेटर का आविष्कार

स्किकार्ड के कैलकुलेटर की प्रतिकृति

1623 और 1624 में, विल्हेम स्किकार्ड ने, जोहान्स केप्लर को भेजे गए दो पत्रों में, अपने डिजाइन और निर्माण की सूचना दी, जिसे उन्होंने "अरिथमेटिकम ऑर्गेनम" ("अंकगणितीय उपकरण") के रूप में संदर्भित किया, जिसे अंत में रेचनहर (गणना घड़ी) के रूप में वर्णित किया गया था। मशीन को अंकगणित (जोड़, घटाव, गुणा और भाग) के सभी चार मूलभूत कार्यों में सहायता के लिए डिज़ाइन किया गया था। इसके उपयोगों के मध्य, स्किकार्ड ने सुझाव दिया कि यह खगोलीय सारणीओं की गणना के श्रमसाध्य कार्य में सहायता करेगा। मशीन छह अंकों की संख्याओं को जोड़ और घटा सकती है, और घंटी बजाकर इस क्षमता के अतिप्रवाह का संकेत देती है। आधार में जोड़ने वाली मशीन मुख्य रूप से दो बहु-अंकीय संख्याओं को जोड़ने या गुणा करने के कठिन कार्य में सहायता के लिए प्रदान की गई थी। इसके लिए उस पर घूमने योग्य नेपियर की हड्डियों की सरल व्यवस्था की गई थी। इसमें मध्यवर्ती गणनाओं को रिकॉर्ड करने के लिए अतिरिक्त मेमोरी रजिस्टर भी था। जबकि शिकार्ड ने नोट किया कि जोड़ने वाली मशीन कार्य कर रही थी, उनके पत्रों में उल्लेख किया गया था कि उन्होंने जोहान फिस्टर नामक व्यवसायी, घड़ी निर्माता से प्रस्तुत मशीन बनाने के लिए कहा था। पश्चाताप का विषय यह है कि यह आग में या तो अधूरा रहते हुए, या किसी भी स्थिति में डिलीवरी से पूर्व नष्ट हो गया। इसके तुरंत पश्चात स्किकार्ड ने अपना प्रोजेक्ट त्याग दिया। 1635 में तीस वर्ष के युद्ध के समय बुबोनिक प्लेग से उनका और उनके पूर्ण परिवार का परिष्कार हो गया था।

स्किकार्ड की मशीन में घड़ी के व्हील का उपयोग किया गया था, जिन्हें ऑपरेटर इनपुट के बल से क्षतिग्रस्त होने से बचाने के लिए स्थिर बनाया गया था और इसलिए वे भारी थे। प्रत्येक अंक में डिस्प्ले व्हील, इनपुट व्हील और इंटरमीडिएट व्हील का उपयोग किया गया था। कैरी ट्रांसफर के समय ये सभी व्हील कैरी प्राप्त करने वाले अंकों के व्हील के साथ जुड़ जाते हैं।

ब्लेज़ पास्कल ने 1642 में परिष्कृत कैरी मैकेनिज्म के साथ यांत्रिक कैलकुलेटर का आविष्कार किया था। तीन वर्ष के प्रयास और 50 प्रोटोटाइप के पश्चात[21] उन्होंने अपने कैलकुलेटर को जनता के सामने प्रस्तुत किया था। उन्होंने अगले दस वर्षों में इनमें से बीस मशीनों का निर्माण किया था।[22] यह मशीन दो संख्याओं को सीधे जोड़ और घटा सकती थी और पुनरावृत्ति द्वारा गुणा और भाग कर सकती थी। चूंकि, स्किकार्ड की मशीन के विपरीत, पास्कलाइन डायल केवल दिशा में घूम सकता है, प्रत्येक गणना के पश्चात ऑपरेटर को सभी 9s में डायल करने की आवश्यकता होती थी और तत्पश्चात (पुनः शून्य करने की विधि) मशीन के माध्यम से कैरी को प्रसारित करता था।[23] इससे ज्ञात होता है कि कैरी मैकेनिज्म ने व्यवहार में स्वयं कई बार प्रमाणित को किया होगा। यह पास्कलाइन की गुणवत्ता का प्रमाण है क्योंकि 17वीं और 18वीं शताब्दी में मशीन की किसी भी आलोचना में कैरी मैकेनिज्म की समस्या का उल्लेख नहीं किया गया था और तत्पश्चात भी इसे सभी मशीनों पर, उनके रीसेट द्वारा, प्रत्येक समय इसका पूर्ण रूप से परीक्षण किया गया था।Cite error: Closing </ref> missing for <ref> tag [6]

1893 में, जर्मन गणना मशीन के आविष्कारक आर्थर बर्कहार्ट को यदि संभव हो तो लाइबनिज़ की मशीन को चालू स्थिति में रखने के लिए कहा गया था। कैरी में अनुक्रम को त्यागकर उनकी रिपोर्ट अनुकूल थी। [24]

लेबनीज़ ने अपने नाम के पहिये और दो गति वाले कैलकुलेटर के सिद्धांत का आविष्कार किया था, किन्तु चालीस वर्षों के विकास के पश्चात वह ऐसी मशीन का उत्पादन करने में सक्षम नहीं था जो पूर्ण रूप से चालू हो;[25] यह पास्कल के कैलकुलेटर को 17वीं सदी में कार्य करने वाला एकमात्र यांत्रिक कैलकुलेटर बनाता है। लेबनीज़ पिनव्हील कैलकुलेटर का वर्णन करने वाले प्रथम व्यक्ति भी थे।[26] उन्होंने एक बार कहा था कि गणना के श्रम में गुलामों के जैसे घंटे नष्ट करना उत्कृष्ट लोगों के लिए अयोग्य है, जो मशीनों का उपयोग किए जाने पर सुरक्षित रूप से किसी और को सौंपा जा सकता था।[27]

अन्य गणना करने वाली मशीनें

स्किकार्ड, पास्कल और लेबनीज़ अनिवार्य रूप से घड़ी की कल की भूमिका से प्रेरित थे जो सत्रहवीं शताब्दी में अत्यधिक मनाया जाता था।[28] चूँकि, इंटरलिंक्ड गियर्स का सरल-दिमाग वाला अनुप्रयोग उनके किसी भी उद्देश्य के लिए अपर्याप्त था। स्किकार्ड ने सामान ले जाने में सक्षम बनाने के लिए दांत वाले "विकृत गियर" का के उपयोग प्रारम्भ किया था। पास्कल ने अपने प्रसिद्ध भारित सॉटोइर के साथ उस पर सुधार किया। पूर्ण रूप से कार्य करने वाले कैरी मैकेनिज्म के मूल्य पर, लाइबनिट्स चल गाड़ी का उपयोग करने की क्षमता के संबंध में और भी आगे बढ़ गया था।

...मैंने तीसरा डिज़ाइन प्रस्तुत किया जो स्प्रिंग्स द्वारा कार्य करता है और जिसका डिज़ाइन अधिक सरल है। यह वही है, जैसा कि मैंने पहले ही कहा है, जिसका मैंने कई बार उपयोग किया है, अनंत व्यक्तियों की स्पष्ट दृष्टि में छिपा हुआ है और जो अभी भी संचालन क्रम में है। फिर भी, इसमें सदैव सुधार करते हुए, मुझे इसके डिज़ाइन को परिवर्तित करने के कारण मिल गए...

— पास्कल, अंकगणित मशीन को देखने और उसे चलाने की जिज्ञासा रखने वालों के लिए विज्ञापन आवश्यक है (1645)। [29]

जब, कई वर्ष पूर्व, मैंने प्रथम बार ऐसा उपकरण देखा, जिसे ले जाने पर, पैदल चलने वालों के कदमों की संख्या स्वचालित रूप से रिकॉर्ड हो जाती है, तो मुझे तुरंत यह विचार आया कि संपूर्ण अंकगणित को समान प्रकार की मशीनरी के अधीन किया जा सकता है जिससे कि न केवल गिनती अन्यथा जोड़-घटाव, गुणा-भाग भी उपयुक्त व्यवस्थित मशीन द्वारा सरलता से, शीघ्रता से और निश्चित परिणाम के साथ पूर्ण किया जा सकता है।

— लेबनीज़, उसकी गणना मशीन पर (1685) [30]

डायरेक्ट-एंट्री गणना मशीन के लिए घड़ी के सिद्धांत (इनपुट व्हील्स और डिस्प्ले व्हील्स को घड़ी जैसी मैकेनिज्म में जोड़ा जाता है) को 17वीं सदी की प्रौद्योगिकी क्षमताओं के साथ अतिरिक्त इनोवेशन के बिना पूर्ण रूप से प्रभावी गणना मशीन बनाने के लिए प्रारम्भ नहीं किया जा सकता था।[31] क्योंकि संचायक के साथ कैरी को कई स्थानों पर ले जाने पर उनके गियर जाम हो जाते थे। केवल 17वीं शताब्दी की गणना करने वाली घड़ियां जो आज तक बची हुई हैं, उनके पास मशीन-वाइड कैरी मैकेनिज्म नहीं है और इसलिए उन्हें पूर्ण रूप से प्रभावी यांत्रिक कैलकुलेटर नहीं कहा जा सकता है। 18 वीं सदी में इटालियन जॉन पोलेनी द्वारा अधिक सफल गणना घड़ी का निर्माण किया गया था और यह दो-गति की गणना करने वाली घड़ी थी (संख्याएं पूर्व अंकित की जाती हैं और तत्पश्चात उन्हें संसाधित किया जाता है)।

  • 1623 में, हिब्रू और खगोल विज्ञान के जर्मन प्रोफेसर विल्हेम स्किकार्ड ने गणना करने वाली घड़ी डिजाइन की, जिसे उन्होंने जोहान्स केप्लर को लिखे दो अक्षरों पर निर्मित किया था। व्यवसायी द्वारा बनाई जाने वाली प्रथम मशीन इसके निर्माण के समय नष्ट हो गई थी और स्किकार्ड ने 1624 में अपनी परियोजना को त्याग दिया था। ये चित्र वर्षों से विभिन्न प्रकाशनों में दिखाई दिए थे, जो 1718 में माइकल हैंश द्वारा केपलर के पत्रों की पुस्तक के साथ प्रारम्भ हुए थे।[32] किन्तु 1957 में इसे डॉ. फ्रांज हैमर द्वारा लंबे समय से लुप्त यांत्रिक कैलकुलेटर के रूप में प्रथम बार प्रस्तुत किया गया था। 1960 के दशक में प्रथम प्रतिकृति के निर्माण से ज्ञात हुआ कि स्किकार्ड की मशीन का डिज़ाइन अधूरा था और इसलिए इसे कार्य करने के लिए पहियों और स्प्रिंग्स को जोड़ा गया था।[33] इन प्रतिकृतियों के उपयोग से ज्ञात हुआ कि एकल-दांत वाला पहिया, जब गणना घड़ी के अंदर उपयोग किया जाता है, वह अपर्याप्त कैरी प्रणाली था।[34] (पास्कल के प्रति स्किकार्ड देखें)। इसका तात्पर्य यह नहीं था कि इस प्रकार की मशीन का व्यवहार में उपयोग नहीं किया जा सकता है, किन्तु जब ऑपरेटर को रोटेशन का विरोध करने वाले प्रणाली का सामना करना पड़ता है, तो 3 डायल से परे ले जाने की असामान्य परिस्थितियों में ऑपरेटर को पश्चात में प्रचार-प्रसार के लिए ले जाने में सहायता करने की आवश्यकता होगी।
  • 1643 के निकट, रूएन के फ्रांसीसी घड़ी निर्माता ने पास्कल के कार्य के विषय में सुनने के पश्चात, अपने स्वयं के डिजाइन की गणना करने वाली घड़ी बनाने का प्रमाण किया। सूचना सुनते ही पास्कल ने अपने सभी कर्मचारियों को निकाल दिया और अपना कैलकुलेटर विकसित करना विवृत कर दिया था।[35] यह आश्वासन दिए जाने के पश्चात ही कि उनके आविष्कार को शाही विशेषाधिकार द्वारा संरक्षित किया जाएगा, उन्होंने अपनी गतिविधि को पुनः प्रारम्भ किया।[36] इस गणना करने वाली घड़ी के सावधानीपूर्वक परीक्षण से ज्ञात हुआ कि यह उचित प्रकार से कार्य नहीं कर रही थी और पास्कल ने इसे एवोर्टन (गर्भपातित भ्रूण) कहा था।[37][38]
  • 1659 में, इटालियन टीटो लिवियो बुराटिनी ने नौ स्वप्रणाली पहियों वाली मशीन बनाई, इनमें से प्रत्येक पहिये को छोटे कैरी व्हील के साथ जोड़ा गया था।[39] ऑपरेशन के अंत में उपयोगकर्ता को या तो मैन्युअल रूप से प्रत्येक कैरी को अगले अंक में जोड़ना पड़ता था या अंतिम परिणाम बनाने के लिए इन नंबरों को मानसिक रूप से जोड़ना होता था।
  • 1666 में, सैमुअल मोरलैंड ने ऐसी मशीन का आविष्कार किया जिसे पैसे जोड़ने के लिए डिज़ाइन किया गया था,[40] किन्तु यह सही जोड़ने वाली मशीन नहीं थी क्योंकि कैरी को प्रत्येक अंक के ऊपर स्थित छोटे कैरी व्हील में जोड़ा गया था और सीधे अगले अंक में नहीं। यह बुरैटिनी की मशीन से अधिक मिलता-जुलता था। मोरलैंड ने नेपियर की हड्डियों पर आधारित विनिमेय डिस्क के साथ बहुगुणित मशीन भी बनाई।[41][42] इन दोनों मशीनों को साथ लेने पर स्किकार्ड के आविष्कार के समान क्षमता प्रदान की गई, चूँकि यह संदिग्ध है कि मोरलैंड ने कभी स्किकार्ड की गणना घड़ी का सामना किया था।
  • 1673 में, फ्रांसीसी घड़ी निर्माता रेने ग्रिललेट ने क्यूरियोसाइट्ज़ मैथमैटिक्स डे ल'इन्वेंशन डु सीनियर ग्रिलेट, हॉरलॉग्यूर ए पेरिस में गणना मशीन का वर्णन किया जो पास्कल के कैलकुलेटर की तुलना में अधिक सघन और घटाव के लिए प्रतिवर्ती होगी। केवल दो ग्रिलेट मशीनें ज्ञात हैं[43] कोई कैरी मैकेनिज्म नहीं है, नौ स्वप्रणाली डायल की तीन पंक्तियों को प्रदर्शित करता है, उनके पास गुणन और विभाजन के लिए नौ घूमने वाली नेपियर की छड़ भी है। ग्रिलेट के प्रमाण के विपरीत, यह कोई यांत्रिक कैलकुलेटर नहीं था।[44]

18वीं सदी

जोहान-हेलफ्रिच मुलर द्वारा डिजाइन और निर्मित 18वीं सदी की गणना मशीन की प्रतिकृति का विवरण।

अवलोकन

Further information: पिनव्हील कैलकुलेटर and लेबनीज़ व्हील

18वीं सदी में प्रथम यांत्रिक कैलकुलेटर देखा गया जो स्वचालित रूप से गुणा कर सकता था; 1709 में जियोवन्नी पोलेनी द्वारा डिजाइन और निर्मित और लकड़ी से बनी, यह प्रथम सफल गणना करने वाली घड़ी थी। इस सदी में निर्मित सभी मशीनों के लिए, डिवीजन को अभी भी ऑपरेटर को यह निश्चित करने की आवश्यकता थी कि प्रत्येक इंडेक्स पर बार-बार घटाव को कब रोकना है, और इसलिए ये मशीनें केवल अबेकस के जैसे विभाजित करने में सहायता प्रदान कर रही थीं। दोनों पिनव्हील कैलकुलेटर और लेबनीज़ व्हील कैलकुलेटर उनके व्यावसायीकरण के कुछ असफल प्रयासों के साथ बनाए गए थे।

प्रोटोटाइप और सीमित रन

एंटोन ब्रौन से यांत्रिक कैलकुलेटर, दिनांक 1727

* 1709 में, इतालवी जियोवन्नी पोलेनी ऐसा कैलकुलेटर बनाने वाले प्रथम व्यक्ति थे जो स्वचालित रूप से गुणा कर सकता था। इसमें पिनव्हील डिज़ाइन का उपयोग किया गया था, यह प्रथम परिचालन गणना करने वाली घड़ी थी और लकड़ी से बनी थी;[45] उन्होंने यह सुनने के पश्चात इसे नष्ट कर दिया कि एंटोनियस ब्रौन ने वियना में पवित्र रोमन सम्राट चार्ल्स VI को अपने स्वयं के डिजाइन की पिनव्हील मशीन समर्पित करने के लिए 10,000 गुल्डेन्स प्राप्त किए थे।[46]

  • 1725 में, फ्रांसीसी विज्ञान अकादमी ने पास्कल के कैलकुलेटर से प्राप्त गणना मशीन को प्रमाणित किया, जिसे फ्रांसीसी शिल्पकार लेपाइन द्वारा डिजाइन किया गया था। यह मशीन पास्कल के कैलकुलेटर और गणना करने वाली घड़ी के मध्य सेतु थी। कैरी ट्रांसमिशन गणना घड़ी के जैसे एक साथ किया गया था, और इसलिए "मशीन एक साथ कुछ कैरी ट्रांसमिशन से परे जाम हो गई होगी"।[47]
  • 1727 में, जर्मन एंटोन ब्रौन ने वियना में सम्राट चार्ल्स VI को प्रथम पूर्ण रूप से कार्यात्मक चार-ऑपरेशन मशीन प्रस्तुत की थी। यह आकार में बेलनाकार था और स्टील, चांदी और पीतल से बना था; इसे उत्तम प्रकार से सजाया गया था और यह पुनर्जागरण टेबल घड़ी जैसा दिखता था। मशीन के शीर्ष पर उत्कीर्ण सम्राट के प्रति उनके समर्पण में यह भी लिखा है "... अज्ञानी लोगों के लिए जोड़, घटाव, गुणा और यहां तक ​​कि विभाजन करने को सरल बनाता है।[48]
  • 1730 में, फ्रेंच एकेडमी ऑफ साइंसेज ने हिलेरिन डी बोइस्टिसंडेउ द्वारा डिजाइन की गई तीन मशीनों को प्रमाणित किया। पहले वाले ने सिंगल-टूथ कैरी मैकेनिज्म का उपयोग किया, जो कि बोइस्टिसैन्ड्यू के अनुसार, उचित प्रकार से कार्य नहीं करेगा यदि कैरी को दो से अधिक स्थानों पर ले जाना पड़े; दो अन्य मशीनों ने स्प्रिंग्स का उपयोग किया जो मंद-मंद सशस्त्र थे जब तक कि उन्होंने अपनी ऊर्जा प्रस्तावित नहीं की जब कैरी को आगे बढ़ाया जाना था। यह पास्कल के कैलकुलेटर के समान था किन्तु गुरुत्वाकर्षण की ऊर्जा का उपयोग करने के अतिरिक्त बोइस्टिसैंडेउ ने स्प्रिंग्स में संग्रहीत ऊर्जा का उपयोग किया था।[49]
  • 1770 में, जर्मन पादरी, फिलिप मैथौस हैन ने लेबनीज़ के सिलेंडरों पर आधारित दो गोलाकार गणना मशीनों का निर्माण किया था।[50][51] हैन के बहनोई जे सी शूस्टर ने 19वीं सदी के प्रारम्भ में हैन के डिजाइन की कुछ मशीनों का निर्माण किया था।[52]
  • 1775 में, यूनाइटेड किंगडम के तीसरे अर्ल स्टैनहोप, चार्ल्स स्टैनहोप ने पिनव्हील मशीन डिजाइन की। यह आयताकार बॉक्स में साइड में हैंडल के साथ सेट किया गया था। उन्होंने 1777 में लेबनीज़ पहियों का उपयोग करके मशीन भी डिजाइन की थी।[53] 1777 में स्टैनहोप ने लॉजिक डिमॉन्स्ट्रेटर का निर्माण किया, औपचारिक तर्क में समस्याओं के समाधान करने के लिए डिज़ाइन की गई मशीन थी। इस उपकरण ने यांत्रिक प्रकारों से तार्किक समस्याओं के समाधान के लिए नए दृष्टिकोण को प्रारम्भ किया था।[40]
  • 1784 में, जर्मन जोहान-हेलफ्रिच मुलर ने हैन की मशीन के समान मशीन का निर्माण किया था।[54]

उन्नीसवीं सदी

अवलोकन

लुइगी टॉर्ची (आविष्कारक) ने 1834 में प्रथम प्रत्यक्ष गुणन मशीन का आविष्कार किया।[55] जेम्स व्हाइट (1822) के पश्चात यह विश्व की दूसरी की चालित मशीन भी थी।[56]मैकेनिकल कैलकुलेटर उद्योग का प्रारम्भ 1851 में हुआ था। कोलमार के थॉमस ने अपना सरलीकृत एरिथोमीटर निर्धारित किया, जो प्रथम मशीन थी जिसे कार्यालय के वातावरण में दैनिक रूप से उपयोग किया जा सकता था।

40 वर्षों के लिए,[57] अरिथमोमीटर विक्रय के लिए उपलब्ध मात्र यांत्रिक कैलकुलेटर था और सम्पूर्ण विश्व में विक्रय किया जाता था। 1890 तक, लगभग 2,500 अरिथोमीटर विक्रय किये जा चुके थे[58] साथ ही दो लाइसेंसशुदा अरिथमोमीटर क्लोन निर्माताओं (बर्कहार्ट, जर्मनी, 1878 और लेटन, यूके, 1883) से कुछ सौ अधिक फेल्ट और टैरंट, वास्तविक वाणिज्यिक उत्पादन में मात्र अन्य प्रतियोगी, ने तीन वर्षों में 100 कॉम्पटोमीटर विक्रय किये थे।[59]19वीं शताब्दी में चार्ल्स बैबेज की गणना मशीनों के डिजाइन भी देखे गए, सबसे प्रथम उनके डिफरेंस इंजन के साथ, 1822 में प्रारम्भ हुआ, जो प्रथम स्वचालित कैलकुलेटर था क्योंकि यह निरंतर पूर्व ऑपरेशन के परिणामों का आगे के लिए उपयोग करता था, और दूसरा अपने विश्लेषणात्मक इंजन के साथ, जो प्रोग्राम और डेटा को पढ़ने के लिए जैक्वार्ड के कार्ड का उपयोग करने वाला प्रथम प्रोग्रामेबल कैलकुलेटर था, जिसे उन्होंने 1834 में प्रारम्भ किया था, और जिसने 20वे दशक के मध्य में बनाए गए बृहत अभिकलित्र का खाका दिया था।[60]

19वीं शताब्दी के समय उत्पादन में डेस्कटॉप यांत्रिक कैलकुलेटर

उत्पादित डेस्कटॉप कैलकुलेटर

File:Close-up of the front panel of a Thomas Arithmometer.jpg
चल परिणाम कैरिज के साथ थॉमस एरिथमोमीटर का फ्रंट पैनल बढ़ाया गया

* 1851 में, थॉमस डी कॉलमार ने अंक के गुणक विभाजक को विस्थापित करके अपने अंकगणित को सरल बनाया। इसने इसे सरल जोड़ने वाली मशीन बना दिया, किन्तु अनुक्रमित संचायक के रूप में उपयोग की जाने वाली इसकी चलती गाड़ी के लिए धन्यवाद, यह अभी भी ऑपरेटर नियंत्रण के अनुसार सरल गुणन और विभाजन की अनुमति देता है। अंकगणित अब उस समय की निर्माण क्षमताओं के अनुकूल हो गया था, इसलिए थॉमस निरंतर दृढ़ं और विश्वसनीय मशीन का निर्माण कर सकता था।[61] नियमावली मुद्रित की गई और प्रत्येक मशीन को सीरियल नंबर दिया गया। इसके व्यावसायीकरण ने यांत्रिक कैलकुलेटर उद्योग का शुभारंभ किया।[62] बैंकों, बीमा कंपनियों, सरकारी कार्यालयों ने अपने दैनिक कार्यों में अंकगणित का उपयोग करना प्रारम्भ कर दिया, मंद-मंद यांत्रिक डेस्कटॉप कैलकुलेटर कार्यालय में लाए।

  • 1878 में जर्मनी के बर्कहार्ट, थॉमस के अरिथमोमीटर का क्लोन बनाने वाले प्रथम व्यक्ति थे। उस समय तक थॉमस डी कोलमार विश्व में डेस्कटॉप मैकेनिकल कैलकुलेटर के मात्र निर्माता थे और उन्होंने लगभग 1,500 मशीनों का निर्माण किया था।[63] अंततः बीस यूरोपीय कंपनियां द्वितीय विश्व युद्ध तक थॉमस के अंकगणित के क्लोन का निर्माण करेंगी।
  • डोर ई. फेल्ट, यू.एस. में, 1886 में कॉम्पटोमीटर का पेटेंट कराया। यह प्रथम सफल कुंजी-चालित जोड़ने और गणना करने वाली मशीन थी। [की-चालित इस तथ्य को संदर्भित करता है कि केवल कुंजियों को दबाने से परिणाम की गणना हो जाती है, कोई भिन्न लीवर या क्रैंक को संचालित नहीं करना पड़ता है। अन्य मशीनों को कभी-कभी की-सेट कहा जाता है।] 1887 में, उन्होंने फेल्ट एंड टैरेंट मैन्युफैक्चरिंग कंपनी बनाने के लिए रॉबर्ट टैरेंट के साथ जुड़ गए।[64] कॉम्पटोमीटर-प्रकार कैलकुलेटर 1961 में ऑल-इलेक्ट्रॉनिक कैलकुलेटर इंजन प्राप्त करने वाली प्रथम मशीन थी (यूके के समलॉक कॉम्पटोमीटर द्वारा निर्धारित किया गया समलॉक एएनआईटीए कैलकुलेटर)।
  • 1890 में विलिगोड्ट टेओफिल ओडनेर टी को कोनिग्सबर्गर एंड सी से अपने कैलकुलेटर के निर्माण का अधिकार वापस मिल गया, जिसने उन्हें 1878 में प्रथम बार पेटेंट कराने के पश्चात से रखा था, किन्तु वास्तव में कुछ भी उत्पादन नहीं किया था। ओडनेर ने अपने कैलकुलेटर के निर्माण के लिए अपनी सेंट पीटर्सबर्ग कार्यशाला का उपयोग किया और उन्होंने 1890 में 500 मशीनों का निर्माण और विक्रय किया। यह निर्माण कार्य 1918 में 23,000 मशीनों के उत्पादन के साथ निश्चित रूप से विवृत हो गया। ओधनेर अरिथोमीटर पिनव्हील इंजन के साथ थॉमस डी कोलमार के अरिथोमीटर का नया डिज़ाइन किया गया संस्करण था, जिसने इसे बनाने के लिए निकृष्ट बना दिया और समान उपयोगकर्ता अंतरापृष्ठ होने का लाभ रखते हुए इसे छोटा पदचिह्न दिया।[65]
  • 1892 में ओडनेर ने अपने कारखाने की बर्लिन शाखा को बेच दिया, जिसे उन्होंने वर्ष पूर्व ग्रिम, नतालिस एंड कंपनी का निर्माण किया था। ब्राउनश्वेग शहर)।[66] यह कई कंपनियों में से प्रथम थी जो सम्पूर्ण विश्व में ओडनेर की मशीन के क्लोनों की बिक्री और निर्माण करेगी; अंततः 1970 के दशक में लाखों की बिक्री हुई।[65]* 1892 में, विलियम सीवार्ड बरोज ने अपने प्रिंटिंग एडिंग कैलकुलेटर का व्यावसायिक निर्माण प्रारम्भ किया[67] बरोज़ कॉर्पोरेशन लेखा मशीन और कंप्यूटर व्यवसायों में अग्रणी कंपनियों में से बन गया।
  • द मिलियनेयर (कैलकुलेटर) कैलकुलेटर 1893 में प्रस्तुत किया गया था। यह किसी भी अंक से सीधे गुणा करने की अनुमति देता है, गुणक में प्रत्येक अंक के लिए क्रैंक का मोड़, इसमें यांत्रिक उत्पाद लुकअप सारणी सम्मिलित थी, जो भिन्न-भिन्न पदों की लंबाई से इकाइयां और दस अंक प्रदान करती थी।[68] अन्य प्रत्यक्ष गुणक मून-हॉपकिन्स बिलिंग मशीन का भाग था, उस कंपनी को 20वीं शताब्दी के प्रारम्भ में बरोज़ द्वारा अधिग्रहित कर लिया गया था।
लकड़ी के डिब्बे में 19वीं सदी का कॉम्पटोमीटर
19वीं और 20वीं सदी के प्रारम्भ में गणना करने वाली मशीनें, म्यूसी डेस आर्ट्स एट मेटियर्स
ओडनेर का अंकगणितमापी

स्वचालित यांत्रिक कैलकुलेटर

लंदन साइंस म्यूज़ियम का वर्किंग डिफ़रेंस इंजन, चार्ल्स बैबेज के डिज़ाइन के डेढ़ सदी पश्चात बनाया गया था।

* 1822 में, चार्ल्स बैबेज ने छोटी कॉगव्हील असेंबली प्रस्तुत की जिसने उनके अंतर इंजन के संचालन का प्रदर्शन किया,[69] यांत्रिक कैलकुलेटर जो 31 दशमलव अंकों की सात संख्याओं को धारण करने और उनमें परिवर्तन करने में सक्षम होगा। यह प्रथम बार था, कि गणना मशीन अपने पूर्व कार्यों से इनपुट परिणामों के रूप में स्वचालित रूप से कार्य कर सकती थी।[60]यह प्रिंटर का उपयोग करने वाली प्रथम गणना मशीन थी। इस मशीन का विकास, जिसे पश्चात में डिफरेंस इंजन नंबर 1 कहा गया, 1834 के निकटतम रुक गई।[70]

  • 1847 में, बैबेज ने उत्तम अंतर इंजन डिजाइन पर कार्य करना प्रारम्भ किया। उसका अंतर इंजन नंबर 2 इनमें से कोई भी डिजाइन पूर्ण रूप से बैबेज द्वारा नहीं बनाया गया था। 1991 में विज्ञान संग्रहालय (लंदन) ने 19वे दशक में उपलब्ध प्रविधि और सामग्रियों का उपयोग करके कार्यशील अंतर इंजन नंबर 2 बनाने की बैबेज की योजना का अनुसरण किया।
  • 1855 में, पेर जॉर्ज शेयुत्ज़ ने बैबेज के डिज़ाइन के आधार पर कार्यशील अंतर इंजन पूर्ण किया। मशीन पियानो के आकार की थी, और 1855 में पेरिस में प्रदर्शनी यूनिवर्स (1855) में प्रदर्शित की गई थी। इसका उपयोग लघुगणक की सारणी बनाने के लिए किया गया था।
  • 1875 में, मार्टिन वाईबर्ग ने बैबेज डिफरेंस इंजन को तत्पश्चात डिजाइन किया और सिलाई मशीन के आकार का संस्करण बनाया।

प्रोग्राम करने योग्य यांत्रिक कैलकुलेटर

1906 के निकटतम बैबेज के बेटे द्वारा समाप्त किए गए विश्लेषणात्मक इंजन से मिल का न्यूनतम किन्तु कार्यकाजी प्रदर्शन भाग

* 1834 में, बैबेज ने अपने विश्लेषणात्मक इंजन को डिजाइन करना प्रारम्भ किया, जो आधुनिक मेनफ़्रेम कंप्यूटर का निर्विवाद पूर्वज बन जाएगा।[71] डेटा और प्रोग्राम के लिए दो भिन्न-भिन्न इनपुट स्ट्रीम (आदिम हार्वर्ड वास्तुकला ), आउटपुट परिणाम के लिए प्रिंटर (तीन भिन्न-भिन्न प्रकार), प्रोसेसिंग यूनिट (मिल), मेमोरी (स्टोर) और प्रोग्रामिंग निर्देशों का प्रथम सेट हॉवर्ड ऐकेन ने 1937 में हार्वर्ड मार्क के लिए वित्त पोषण का अनुरोध करते हुए आईबीएम को जो प्रस्ताव दिया था, जो कंप्यूटर उद्योग में आईबीएम की प्रवेश मशीन बन गया था, हम पढ़ सकते हैं, कुछ गणना मशीनों को वैज्ञानिक परिक्षण के लिए सामर्थ्य से डिजाइन किया गया है, उल्लेखनीय अपवाद ये हैं चार्ल्स बैबेज और उनके पश्चात आने वाले अन्य लोगों के बारे में। 1812 में बैबेज ने गणितीय कार्यों की सारणीओं की गणना और मुद्रण के लिए उपयोग की जाने वाली पहले की तुलना में उच्च प्रकार की गणना मशीन के विचार की कल्पना की। डिफरेंस इंजन को त्यागने के पश्चात, बैबेज ने अपनी ऊर्जा डिफरेंस इंजन की तुलना में कहीं अधिक शक्तियों के विश्लेषणात्मक इंजन के डिजाइन और निर्माण के लिए समर्पित की।[72]

  • 1843 में, विश्लेषणात्मक इंजन पर फ्रांसीसी लेख के अनुवाद के समय, लवलेस है ने बर्नौली संख्याओं की गणना करने के लिए एल्गोरिद्म लिखा, जिसमें उन्होंने सम्मिलित किए गए कई नोट्स में से में लिखा था। इसे प्रथम कंप्यूटर प्रोग्राम माना जाता है।
  • 1872 से 1910 तक, हेनरी बैबेज ने अपने पिता की मशीन की केंद्रीय प्रसंस्करण इकाई मिल बनाने पर रुक-रुक कर कार्य किया। कुछ असफलताओं के पश्चात, उन्होंने 1906 में मिल का सफल प्रदर्शन दिया, जिसमें पाई के प्रथम 44 गुणकों को 29 स्थानों के अंकों के साथ मुद्रित किया गया।

कैश रजिस्टर

Further information: कैश-रजिस्टर

1879 में अमेरिकी सलूनकीपर जेम्स रिट्टी द्वारा आविष्कृत कैश रजिस्टर ने व्यापार आदान-प्रदान में अव्यवस्था और बेईमानी की प्राचीन समस्याओं को संबोधित किया।[73] यह जोड़ने वाली मशीन थी जिसमें प्रिंटर (कंप्यूटिंग), घंटी और दोनों ओर डिस्प्ले था, जो अवहेलना करने वाली पार्टी और स्टोर के मालिक को दिखाता था, यदि वह चाहता था, तो वर्तमान आदान-प्रदान के लिए परिवर्तित किये गए धन की राशि कैश रजिस्टर का उपयोग करना सरल था और वास्तविक यांत्रिक कैलकुलेटर के विपरीत, बड़ी संख्या में व्यवसायों द्वारा आवश्यक और शीघ्र से अपनाया गया था। 1888 और 1895 के मध्य चौरासी कंपनियों ने कैश रजिस्टर बेचे, किसी भी लम्बाई के लिए केवल तीन ही बच पाए।[74]1890 में, जॉन हेनरी पैटरसन (एनसीआर के मालिक) द्वारा एनसीआर निगम प्रारम्भ करने के 6 वर्ष पश्चात, अकेले उनकी कंपनी द्वारा 20,000 मशीनों की बिक्री की गई थी, जबकि सभी वास्तविक कैलकुलेटरों की कुल संख्या लगभग 3,500 थी।[75]1900 तक, एनसीआर ने 200,000 कैश रजिस्टर बनाए थे[76] और थॉमस एरिथमोमीटर कंपनी की तुलना में उनका निर्माण करने वाली और भी कंपनियां थीं, जो अभी लगभग 3,300 बेची थीं[77] और बरोज़ ने केवल 1,400 मशीनें बेचीं।[78]

प्रोटोटाइप और सीमित रन

1820 से 1851 तक बनाए गए अंकगणित में अंक का गुणक/विभाजक कर्सर (हाथीदांत शीर्ष) बाईं ओर है। इन मशीनों के केवल प्रोटोटाइप बनाए गए थे।

* 1820 में, थॉमस डी कॉलमार ने एरिथोमीटर का पेटेंट कराया। यह वास्तविक चार ऑपरेशन मशीन थी जिसमें अंक गुणक विभाजक (द मिलियनेयर (कैलकुलेटर) 70 वर्ष पश्चात निर्धारित किया गया था, जिसमें समान यूजर अंतरापृष्ठ था[79])। उन्होंने अपनी मशीन को विकसित करने में आगामी 30 वर्ष और 300,000 फ़्रैंक व्यय किए।[80] इस डिज़ाइन को 1851 में सरलीकृत अरिथमोमीटर द्वारा प्रतिस्थापित किया गया था जो केवल जोड़ने वाली मशीन थी।

  • 1840 से, डिडिएर रोथ ने पेटेंट कराया और कुछ गणना मशीनों का निर्माण किया, जिनमें से पास्कल के कैलकुलेटर का प्रत्यक्ष वंशज था।
  • 1842 में, टिमोलन मौरेल ने अरिथमौरेल का आविष्कार किया, जो एरिथमोमीटर पर आधारित था, जो मशीन में केवल उनके मान अंकित करके दो संख्याओं को गुणा कर सकता था।
  • 1845 में, इज़राइल अब्राहम स्टाफ़ेल ने प्रथम बार ऐसी मशीन का प्रदर्शन किया जो जोड़ने, घटाने, विभाजित करने, गुणा करने और वर्गमूल प्राप्त करने में सक्षम थी।
  • 1854 के निकटतम, आंद्रे मिशेल गुएरी ने ऑरडोनेटर स्टेटिस्टिक का आविष्कार किया, बेलनाकार उपकरण जिसे नैतिक चर (अपराध, आत्महत्या, आदि) पर डेटा के मध्य संबंधों को सारांशित करने में सहायता के लिए डिज़ाइन किया गया था।[81]
  • 1872 में, फ्रैंक स्टीफन बाल्डविन अमेरिका में फ्रैंक एस. बाल्डविन ने पिनव्हील कैलकुलेटर का आविष्कार किया।
  • 1877 में संयुक्त राज्य अमेरिका में बोस्टन के जॉर्ज बी ग्रांट ने जोड़, घटाव, गुणा और भाग करने में सक्षम अनुदान यांत्रिक गणना मशीन का उत्पादन प्रारम्भ किया।[82] मशीन का माप 13x5x7 इंच था और इसमें पीतल और टेम्पर्ड स्टील से बने अस्सी वर्किंग पीस थे। यह प्रथम बार फिलाडेल्फिया में 1876 शताब्दी प्रदर्शनी में जनता के लिए प्रस्तुत किया गया था।[83]
  • 1883 में, यूनाइटेड किंगडम के एडमंडसन ने सर्कुलर स्टेप्ड ड्रम कैलकुलेटर का पेटेंट कराया।[84]
1840 के निकटतम डिडिएर रोथ द्वारा आविष्कार की गई क प्रारंभिक गणना मशीन का विवरण, यह मशीन पास्कल के कैलकुलेटर का प्रत्यक्ष वंशज है।
ग्रांट बैरल, 1877


1900 से 1970 के दशक

Further information: कंप्यूटिंग हार्डवेयर का इतिहास

यांत्रिक कैलकुलेटर अपने चरम पर पहुंच गए हैं

1914 से यांत्रिक कैलकुलेटर
जोड़ और घटाव के लिए योजक का उपयोग किया जा सकता है।

इस समय तक प्रणाली के दो भिन्न-भिन्न वर्ग स्थापित हो गए थे, जो प्रत्यागामी और रोटरी थे। पूर्व प्रकार के प्रणाली को सामान्यतः सीमित-यात्रा वाले हैंड क्रैंक द्वारा संचालित किया जाता था; कुछ आंतरिक विस्तृत ऑपरेशन पुल पर हुए, और अन्य पूर्ण चक्र के प्रस्तावित भाग पर हुए थे। सचित्र 1914 मशीन इस प्रकार है; क्रैंक दाहिनी ओर ऊर्ध्वाधर है। अंत में, इनमें से कुछ प्रणालीों को इलेक्ट्रिक मोटर्स और रिडक्शन गियरिंग द्वारा संचालित किया गया था जो रोटरी गति को पारस्परिक गति में परिवर्तित करने के लिए क्रैंक और कनेक्टिंग छड़ को संचालित करता था।

अंत के प्रकार, रोटरी, में कम से कम मुख्य शाफ्ट होता था जो [या अधिक] निरंतर क्रांति करता था, प्रति मोड़ जोड़ या घटाव करता था। कई डिजाइनों में, विशेष रूप से यूरोपीय कैलकुलेटरों में हैंडक्रैंक और ताले थे, जिससे कि यह सुनिश्चित किया जा सके कि मोड़ पूर्ण होने के पश्चात क्रैंक त्रुटिहीन स्थिति में वापस आ जाएं।

20वीं शताब्दी के पूर्वार्द्ध में यांत्रिक कैलकुलेटर प्रणाली का क्रमिक विकास हुआ था।

डाल्टन ऐड-लिस्टिंग मशीन को 1902 में प्रस्तुत किया गया था, जो केवल दस कुंजियों का उपयोग करने वाली विशेष प्रकार की प्रथम मशीन थी, और कई कंपनियों द्वारा निर्मित 10-कुंजी ऐड-लिस्टर्स के कई भिन्न-भिन्न मॉडलों में से प्रथम बन गई थी।

1948 में बेलनाकार कर्टा कैलकुलेटर, जो हाथ में पकड़ने के लिए पर्याप्त सघन था, 1938 में कर्ट हार्टस्ट्रॉन्ग द्वारा विकसित किए जाने के पश्चात प्रस्तुत किया गया था। यह स्टेप्ड-गियर गणना प्रणाली का चरम विकास था। इसे पूरक जोड़कर घटाया गया; जोड़ने के लिए दांतों के मध्य घटाव के लिए दांत थे।

1900 के दशक के प्रारंभ से 1960 के दशक तक, यांत्रिक कैलकुलेटर डेस्कटॉप कंप्यूटिंग बाजार पर नियंत्रित रहे। संयुक्त राज्य अमेरिका में प्रमुख आपूर्तिकर्ताओं में फ्रिडेन, मोनरो और एससीएम/मार्चेंट सम्मिलित थे। ये उपकरण मोटर चालित थे, और इनमें चलने योग्य गाड़ियां थीं जहां गणना के परिणाम डायल द्वारा प्रदर्शित किए जाते थे। लगभग सभी कीबोर्ड भरे हुए थे - प्रत्येक अंक जिसे अंकित किया जा सकता था, उसमें नौ कुंजियों का अपना कॉलम था, 1..9, साथ ही एक कॉलम-क्लियर कुंजी, जो एक साथ कई अंकों की प्रविष्टि की अनुमति देती थी। (मार्केंट फिगरमैटिक के नीचे दिए गए चित्रण को देखें।) दस-कुंजी सीरियल प्रविष्टि के विपरीत, इसे समानांतर प्रविष्टि कहा जा सकता है जो यांत्रिक जोड़ने वाली मशीनों में सामान्य थी, और अब इलेक्ट्रॉनिक कैलकुलेटर में सार्वभौमिक है। (लगभग सभी फ्रिडेन कैलकुलेटर, साथ ही साथ कुछ रोटरी (जर्मन) डाइहल्स में गुणन करते समय गुणक में प्रवेश करने के लिए दस-कुंजी सहायक कीबोर्ड होता था।) पूर्ण कीबोर्ड में सामान्यतः दस कॉलम होते थे, चूँकि कुछ कम व्यय वाली मशीनों में आठ होते थे। उल्लिखित तीन कंपनियों द्वारा बनाई गई अधिकांश मशीनों ने अपने परिणाम मुद्रित नहीं किए, चूँकि ओलिवेत्ति जैसी अन्य कंपनियों ने प्रिंटिंग कैलकुलेटर बनाया था।

इन मशीनों में, जोड़ और घटाव एक ही ऑपरेशन में किया जाता था, जैसा कि पारंपरिक जोड़ने वाली मशीन पर होता है, किन्तु गुणा और विभाजन बार-बार यांत्रिक जोड़ और घटाव द्वारा पूर्ण किया जाता था। फ्रिडेन ने कैलकुलेटर निर्मित किया गया जो वर्गमूल भी प्रदान करता था, मूल रूप से विभाजन करके, किन्तु अतिरिक्त प्रणाली के साथ जो व्यवस्थित रूप से कीबोर्ड में संख्या को स्वचालित रूप से बढ़ाता था। यांत्रिक कैलकुलेटर के अंतिम में शॉर्ट-कट गुणन होने की संभावना थी, और कुछ दस-कुंजी, सीरियल-एंट्री प्रकारों में दशमलव-बिंदु कुंजियाँ थीं। चूँकि, दशमलव-बिंदु कुंजियों को महत्वपूर्ण आंतरिक अतिरिक्त जटिलता की आवश्यकता होती थी, और केवल अंतिम डिजाइनों में ही प्रस्तुत किया गया था। 1948 कर्टा जैसे हैंडहेल्ड यांत्रिक कैलकुलेटर का उपयोग 1970 के दशक में इलेक्ट्रॉनिक कैलकुलेटर द्वारा विस्थापित किए जाने तक निरंतर रहा था।

ट्रिउम्फाटोर सीआरएन1 (1958)
वाल्थर डब्लूएसआर160 (मध्य यूरोप में सबसे सामान्य कैलकुलेटर में से था।) (1960)
डाल्टन जोड़ने की मशीन (सीए 1930)
यांत्रिक कैलकुलेटर का प्रणाली
मर्सिडीज यूक्लिडिश, मॉड 29 संग्रहालय यूरोपाइशर कुल्टुरेन में

विशिष्ट यूरोपीय चार-संचालन मशीनें ओडनर प्रणाली, या इसकी विविधताओं का उपयोग करती हैं। इस प्रकार की मशीन में मूल ओडनेर, ब्रंसविगा और ट्रायम्फेटर, थेल्स, वाल्थर, फेसिट से तोशिबा तक प्रारम्भ होने वाले कई अनुकरणकर्ता सम्मिलित थे। चूँकि इनमें से अधिकांश हैंडक्रैंक द्वारा संचालित थे, किन्तु मोटर चालित संस्करण भी थे। हैमन कैलकुलेटर बाहरी रूप से पिनव्हील मशीनों से मिलते जुलते थे, किन्तु सेटिंग लीवर ने कैम को प्रस्तुत किया था, जो डायल के अधिक दूर चले जाने पर ड्राइव पाउल को निष्क्रिय कर देता था।

चूँकि डाल्टन ने 1902 में प्रथम 10-कुंजी प्रिंटिंग एडिंग (दो ऑपरेशन, दूसरी घटाव वाली) मशीन प्रस्तुत की, ये विशेषताएं कई दशकों तक कंप्यूटिंग (चार ऑपरेशन) मशीनों में उपस्थित नहीं थीं। फैसिट-टी (1932) बड़ी संख्या में बेची जाने वाली प्रथम 10-कुंजी कंप्यूटिंग मशीन थी। ओलिवेटी डिविसुम्मा-14 (1948) प्रिंटर और 10-कुंजी कीबोर्ड दोनों के साथ प्रथम कंप्यूटिंग मशीन थी।

1960 के दशक तक मोटर चालित सहित पूर्ण-कीबोर्ड मशीनें भी बनाई गईं थीं। यूरोप में प्रमुख निर्माताओं में मर्सिडीज-यूक्लिड, आर्किमिडीज़ और मैडास थे। संयुक्त राज्य अमेरिका में, फ्रिडेन, मर्चेंट और मोनरो कैरिज के साथ रोटरी कैलकुलेटर के प्रमुख निर्माता थे। रेसिप्रोकेटिंग कैलकुलेटर (जिनमें से अधिकांश मशीनें जोड़ रहे थे, कई इंटीग्रल प्रिंटर के साथ थे) रेमिंगटन रैंड और बरोज़ द्वारा बनाए गए थे। ये सभी कुंजी-सेट थे। फेल्ट और टैरंट ने कॉम्पटोमीटर और साथ ही विक्टर को बनाया, जो कुंजी-चालित थे।

फ्रिडेन और मोनरो का मूल प्रणाली संशोधित लाइबनिज़ व्हील था (उत्तम ज्ञात, संभवतः अनौपचारिक रूप से, संयुक्त राज्य अमेरिका में स्टेप्ड ड्रम या स्टेप रेकनर के रूप में)। फ्रिडेन में मशीन की बॉडी और संचायक डायल के मध्य प्राथमिक रिवर्सिंग ड्राइव थी, इसलिए इसका मुख्य शाफ्ट सदैव ही दिशा में घूमता था। स्विस मैडास समान था। चूंकि, मुनरो ने अपने मुख्य शाफ्ट की दिशा को घटाना उलट दिया।

प्रारंभिक मर्चेंट पिनव्हील मशीन थे, किन्तु उनमें से अधिकतम उल्लेखनीय रूप से परिष्कृत रोटरी प्रकार के थे। यदि [+] बार को नीचे रखा जाता है, तो वे प्रति मिनट 1,300 अतिरिक्त चक्रों पर दौड़ते हैं। अन्य 600 चक्र प्रति मिनट तक सीमित थे, क्योंकि उनके संचायक डायल प्रत्येक चक्र के लिए प्रारम्भ और रुके थे, निरंतर चक्रों के लिए मर्चेंट डायल स्थिर और आनुपातिक गति से चले गए। अधिकांश मर्चेंट्स के निकट चरम दाहिनी ओर नौ कुंजियों की पंक्ति थी, जैसा कि फिगरमैटिक के चित्र में दिखाया गया है। ये बस मशीन को कुंजी पर संख्या के अनुरूप चक्रों की संख्या के लिए जोड़ते हैं, और तत्पश्चात गाड़ी को स्थान पर स्थानांतरित कर देते हैं। यहां तक ​​कि नौ जोड़ चक्रों में भी अधिक कम समय लगा।

मर्चेंट में, चक्र के प्रारम्भ के निकट, संचायक डायल कवर में संवृत से दूर, डिप में नीचे की ओर चले गए। उन्होंने मशीन के पिंड में ड्राइव गियर लगाए, जो उन्हें उनके द्वारा खिलाए जाने वाले अंक के अनुपात में गति से घुमाते थे, डायल द्वारा उनके दाहिनी ओर बनाए गए कैरीज़ से अतिरिक्त गति (10: 1 कम) के साथ चक्र के पूर्ण होने पर, डायल पारंपरिक वाट-घंटे मीटर में पॉइंटर्स के ओर अनुचित हो जाएंगे। चूंकि, जैसे ही वे डुबकी से बाहर आए, निरंतर-लीड डिस्क कैम ने उन्हें (सीमित-यात्रा) स्पर-गियर अंतर के माध्यम से पुनः प्राप्त किया। साथ ही, निचले ऑर्डर के कैर्री को दूसरे, ग्रहों के अंतर से जोड़ा गया। (दिखाई गई मशीन के [20-अंकीय] संचायक में 39 अंतर हैं!)

किसी भी यांत्रिक कैलकुलेटर में, वास्तव में गियर, सेक्टर, या कुछ इसी प्रकार की डिवाइस संचायक को गियर के दांतों की संख्या से स्थानांतरित करती है, जो अंकों को जोड़े या घटाए जाने से मेल खाती है। तीन दांत तीन की गिनती से स्थिति परिवर्तित करते हैं। मूल कैलकुलेटर प्रणाली के अधिकांश भाग संचायक को प्रारम्भ करके, तत्पश्चात स्थिर गति से चलते हुए, और रुकते हुए स्थानांतरित करते हैं। विशेष रूप से, रुकना महत्वपूर्ण है, क्योंकि तीव्रता से संचालन प्राप्त करने के लिए संचायक को शीघ्र स्थानांतरित करने की आवश्यकता होती है। जिनेवा ड्राइव के वेरिएंट सामान्यतः ओवरशूट को ब्लॉक करते हैं (जो निश्चित रूप से अनुचित परिणाम देगा)।

चूंकि, दो भिन्न-भिन्न मूल प्रणाली, मर्सिडीज-यूक्लिड और मर्चेंट, डायल को जोड़े या घटाए जाने वाले अंक के अनुरूप गति से ले जाते हैं; a [1] संचायक को सबसे मंद और a [9] सबसे तीव्र चलाता है। मर्सिडीज-यूक्लिड में, लंबा स्लॉटेड लीवर, छोर पर घूमता है, नौ रैक (सीधे गियर) को लीवर की धुरी से उनकी दूरी के अनुपात में अंत तक ले जाता है। प्रत्येक रैक में ड्राइव पिन होता है जिसे स्लॉट द्वारा स्थानांतरित किया जाता है। [1] के लिए रैक निश्चित रूप से पिवट के सबसे निकट है। प्रत्येक कीबोर्ड अंक के लिए, स्लाइडिंग चयनकर्ता गियर, जैसा कि लेबनीज़ व्हील में होता है, उस रैक को संलग्न करता है, जो अंकित किए गए अंक से मेल खाता है। निःसंदेह, संचायक या तो आगे या रिवर्स स्ट्रोक पर परिवर्तित होता है, किन्तु दोनों में नहीं, यह प्रणाली निर्माण के लिए विशेष रूप से सरल और अपेक्षाकृत सरल है।

मर्चेंट, चूँकि, इसके दस स्तंभों में से प्रत्येक के लिए, मशीन के पिंड के शीर्ष पर इसके आउटपुट स्पर गियर के साथ नौ-अनुपात प्रीसेलेक्टर ट्रांसमिशन है; वह गियर संचायक गियरिंग को संलग्न करता है। जब कोई इस प्रकार के संचरण में दांतों की संख्या निकालने का प्रयत्न करता है, तो यह सीधी विधि है, ऐसे प्रणाली पर विचार करने के लिए प्रेरित करता है जो यांत्रिक गैसोलीन पंप रजिस्टरों में होता है, जिसका उपयोग कुल मूल्य को इंगित करने के लिए किया जाता है। चूँकि, यह प्रणाली गंभीर रूप से भारी है, और कैलकुलेटर के लिए पूर्ण रूप से अव्यावहारिक है, गैस पंप में 90-टूथ गियर मिलने की संभावना है। कैलकुलेटर के कंप्यूटिंग भागों में प्रैक्टिकल गियर में 90 दांत नहीं हो सकते। वे या तो अधिक बड़े होंगे, या अधिक नाजुक होंगे।

यह देखते हुए कि प्रति स्तंभ नौ अनुपात महत्वपूर्ण जटिलता को दर्शाता है, मर्चेंट में सभी में कुछ सौ भिन्न-भिन्न गियर होते हैं, इसके संचायक में कई मूल रूप से, संचायक डायल को [1] के लिए 36 डिग्री ( मोड़ का 1/10) और [9] के लिए 324 डिग्री ( मोड़ का 9/10) घुमाना पड़ता है, जिससे आने वाली वहन की अनुमति नहीं होती है। गियरिंग में किसी बिंदु पर, दांत को [1] के लिए, और नौ दांतों को [9] के लिए पारित करने की आवश्यकता होती है। ड्राइवशाफ्ट से आवश्यक गति को विकसित करने की कोई विधि नहीं है जो दांतों की व्यावहारिक (अपेक्षाकृत छोटी) संख्या वाले कुछ गियर के साथ प्रति चक्र क्रांति को घुमाता है।

इसलिए, मर्चेंट के पास छोटे प्रसारणों को खिलाने के लिए तीन ड्राइवशाफ्ट हैं। चक्र के लिए, वे 1/2, 1/4 और 1/12 चक्कर लगाते हैं। 1/2-टर्न शाफ्ट में (प्रत्येक कॉलम के लिए) 12, 14, 16 और 18 दांतों के साथ गियर होते हैं, जो अंक 6, 7, 8 और 9 के अनुरूप होते हैं। 1/4-टर्न शाफ्ट वहन करता है (प्रत्येक कॉलम भी) ) 3, 4, और 5 के लिए 12, 16, और 20 दांत वाले गियर अंक [1] और [2] 1/12-क्रांति शाफ्ट पर 12 और 24-दांत गियर द्वारा नियंत्रित किए जाते हैं। प्रैक्टिकल डिज़ाइन 12वें रेव को रखता है। शाफ्ट अधिक दूर है, इसलिए 1/4-टर्न शाफ्ट स्वप्रणाली रूप से घूमने वाले 24 और 12-टूथ आइडलर गियर ले जाता है। घटाव के लिए, ड्राइवशाफ्ट ने दिशा उलट दी।

चक्र के प्रारंभिक भाग में, पांच पेंडेंट में से चयनित अंक के लिए उपयुक्त ड्राइव गियर संलग्न करने के लिए ऑफ-सेंटर चलता है।

कुछ मशीनों के सम्पूर्ण कीबोर्ड में 20 कॉलम तक होते थे। इस क्षेत्र में राक्षस बरोज़ कॉर्पोरेशन द्वारा प्रदर्शन उद्देश्यों के लिए बनाया गया डुओडेसिलियन था।

स्टर्लिंग मुद्रा के लिए, £/s/d (और यहां तक ​​कि फार्थिंग्स), मूल प्रणालीों की विविधताएं थीं, विशेष रूप से विभिन्न संख्या में गियर दांत और संचायक डायल स्थिति, शिलिंग्स और पेंस को समायोजित करने के लिए, दस अंकों [s] के लिए अतिरिक्त कॉलम जोड़े गए, शिलिंग्स के लिए 10 और 20, और पेंस के लिए 10 निःसंदेह, ये मूलांक -20 और मूलांक -12 प्रणाली के रूप में कार्य करते हैं।

मर्चेंट का प्रकार, जिसे बाइनरी-ऑक्टल मर्चेंट कहा जाता है, मूलांक -8 (ऑक्टल) मशीन थी। इसे स्थिरता के लिए अधिक प्रारंभिक वैक्यूम-ट्यूब (वाल्व) बाइनरी कंप्यूटरों की परिक्षण के लिए बेचा गया था। (उस समय, यांत्रिक कैलकुलेटर ट्यूब/वाल्व कंप्यूटर की तुलना में अधिक अधिक विश्वसनीय था।)

साथ ही, जुड़वां मर्चेंट था, जिसमें सामान्य ड्राइव क्रैंक और रिवर्सिंग गियरबॉक्स के साथ दो पिनव्हील मर्चेंट सम्मिलित थे।[85] जुड़वां मशीनें अपेक्षाकृत दुर्लभ थीं, और प्रत्यक्ष रूप से गणनाओं के सर्वेक्षण के लिए उपयोग की जाती थीं। कम से कम ट्रिपल मशीन बनाई गई थी।

फेसिट कैलकुलेटर, और इसके समान, मूल रूप से पिनव्हील मशीन हैं, किन्तु कैरिज के अतिरिक्त पिनव्हील्स की सारणी निकट में चलती है। पिनविल्स बिकिनरी हैं; अंक 1 से 4 सतह से विस्तार करने के लिए स्लाइडिंग पिन की इसी संख्या का कारण बनता है; अंक 5 से 9 भी पांच-दांत वाले क्षेत्र के साथ-साथ 6 से 9 के लिए ही पिन का विस्तार करते हैं।

कुंजिया उन कैमरों को संचालित करती हैं, जो पूर्व पिन-पोजिशनिंग कैम को अनलॉक करने के लिए स्विंगिंग लीवर को संचालित करते हैं, जो पिनव्हील प्रणाली का भाग है; लीवर की आगे की गति (कुंजी के कैम द्वारा निर्धारित राशि द्वारा) पिन की आवश्यक संख्या को बढ़ाने के लिए पिन-पोजिशनिंग कैम को घुमाती है।[86]स्टाइलस के लिए सर्कुलर स्लॉट के साथ स्टाइलस-संचालित एडर्स और स्टर्लिंग प्लास्टिक्स (यूएसए) द्वारा बनाए गए साइड-बाय-साइड व्हील्स में यथार्थ कैर्री सुनिश्चित करने के लिए सरल एंटी-ओवरशूट प्रणाली थी।

कर्टा टाइप I
डुओडेसिलियन (सीए 1915)
मर्चेंट फिगरमैटिक (1950-52)
फ्रिडेन कैलकुलेटर
फेसिट एनटीके (1954)
ओलिवेटी डिविसुम्मा 24 इंटीरियर, (1964)
ओडनेर अरिथ्मोमीटर (1890-1970)

युग का अंत

1970 के दशक के प्रारम्भ में यांत्रिक कैलकुलेटरों की बिक्री निरंतर रही, चूँकि शीघ्रता से घटती संख्या में, कई निर्माता विवृत हो गए या उनका अधिग्रहण कर लिया गया। कॉम्पटोमीटर प्रकार के कैलकुलेटर प्रायः कर्तव्यों को जोड़ने और सूचीबद्ध करने के लिए उपयोग किए जाने के लिए अधिक लंबे समय तक बनाए रखा जाता था, विशेष रूप से लेखांकन में, क्योंकि प्रशिक्षित और कुशल ऑपरेटर संख्या के सभी अंकों को कॉम्पटोमीटर पर हाथों के आंदोलन में तीव्रता से अंकित कर सकता था। 10-कुंजी इलेक्ट्रॉनिक कैलकुलेटर के साथ वास्तव में, केवल कम संख्या वाली कुंजियों का उपयोग करके दो स्ट्रोक में बड़े अंक अंकित करना तीव्रता थी; उदाहरण के लिए, 9 को 4 के पश्चात 5 के रूप में अंकित किया जाएगा। कुछ की-चालित कैलकुलेटर में प्रत्येक कॉलम के लिए कुंजियाँ थीं, किन्तु केवल 1 से 5 तक; वे संगत रूप से सघन थे। साधारण इलेक्ट्रॉनिक कैलकुलेटर के अतिरिक्त कंप्यूटर के प्रसार ने कॉम्पटोमीटर का अंत कर दिया। साथ ही, 1970 के दशक के अंत तक, स्लाइड नियम अप्रचलित हो गया था।

यह भी देखें

संदर्भ

  1. ↑ Michael Williams, History of Computing Technology, IEEE Computer Society, p. 122 (1997)
  2. ↑ Michael Williams, History of Computing Technology, IEEE Computer Society, p. 124, 128 (1997)
  3. ↑ Prof. René Cassin, Pascal tercentenary celebration, London, (1942), Magazine Nature
  4. ↑ 4.0 4.1 Jean Marguin (1994), p. 48
  5. ↑ See Pascal's calculator#Competing designs
  6. ↑ 6.0 6.1 Jean Marguin, p. 64-65 (1994)
  7. ↑ Smith 1929, pp. 173–181
  8. ↑ Beside two arithmometer clone makers from Germany and England, the only other company to offer calculators for sale was Felt & Tarrant from the USA which started selling their comptometer in 1887 but had only sold 100 machines by 1890.
  9. ↑ Ernst Martin p. 133 (1925)
  10. ↑ Ernst Martin p. 23 (1925)
  11. ↑ #MARG,Jean Marguin p. 171, (1994)
  12. ↑ Anthony Hyman, Charles Babbage, pioneer of the computer, 1982
  13. ↑ "The introduction of punched cards into the new engine was important not only as a more convenient form of control than the drums, or because programs could now be of unlimited extent, and could be stored and repeated without the danger of introducing errors in setting the machine by hand; it was important also because it served to crystallize Babbage's feeling that he had invented something really new, something much more than a sophisticated calculating machine." Bruce Collier, 1970
  14. ↑ I. Bernard Cohen, p. 66-67, (2000)
  15. ↑ Brian Randell, p. 187, 1975
  16. ↑ Please see Pascaline#Pascal versus Schickard
  17. ↑ "The arithmetical machine produces effects which approach nearer to thought than all the actions of animals. But it does nothing which would enable us to attribute will to it, as to the animals.", Pascal, Pensées Bartleby.com, Great Books online, Blaise Pasdcal, Thoughts
  18. ↑ Magazine Nature, (1942)
  19. ↑ Scripta Mathematica, p. 128 (1932)
  20. ↑ From the calculating machine of Pascal to the computer, p. 43 (1990)
  21. ↑ (fr) La Machine d’arithmétique, Blaise Pascal, Wikisource
  22. ↑ Guy Mourlevat, p. 12 (1988)
  23. ↑ #कूरियर, एन ° 8, पी। 9, (1986)
  24. ↑ Scripta Mathematica, p. 149 (1932)
  25. ↑ Morar, Florin-Stefan (March 2015). "Reinventing machines: the transmission history of the Leibniz calculator". The British Journal for the History of Science. 48 (1): 123–146. doi:10.1017/S0007087414000429. ISSN 0007-0874. PMID 25833800. S2CID 38193192.
  26. ↑ David Smith, p. 173-181 (1929)
  27. ↑ As quoted in Smith 1929, pp. 180–181
  28. ↑ See http://things-that-count.net
  29. ↑ Translated from "j'en composai une troisième qui va par ressorts et qui est très simple en sa construction. C'est celle de laquelle, comme j'ai déjà dit, je me suis servi plusieurs fois, au vu et su d'une infinité de personnes, et qui est encore en état de servir autant que jamais. Toutefois, en la perfectionnant toujours, je trouvai des raisons de la changer" Avis nécessaire à ceux qui auront curiosité de voir la Machine d'Arithmétique et de s'en servir Wikisource: La Machine d’arithmétique, Blaise Pascal
  30. ↑ Quoted in David Smith, p. 173, (1929)
  31. ↑ Michael Williams, p. 124, 128 (1997) for Schikard's machine and the fact that the machines built by Burattini, Morland and Grillet were calculating clocks without a completely effective carry mechanism.
  32. ↑ History of computer (retrieved on 1 February 2012)
  33. ↑ Michael Williams, p. 122 (1997)
  34. ↑ Michael Williams, p. 124, 128 (1997)
  35. ↑ "The appearance of this small avorton disturbed me to the utmost and it dampened the enthusiasm with which I was developing my calculator so much that I immediately let go all of my employees..." translated from the French: "L'aspect de ce petit avorton me déplut au dernier point et refroidit tellement l'ardeur avec laquelle je faisais lors travailler à l'accomplissement de mon modèle qu'à l'instant même je donnai congé à tous les ouvriers..."
  36. ↑ "But, later on, Lord Chancellor of France [...] granted me a royal privilege which is not usual, and which will suffocate before their birth all these illegitimate avortons which, by the way, could only be born of the legitimate and necessary alliance of theory and art." translated from the French: "Mais, quelque temps après, Monseigneur le Chancelier [...] par la grâce qu'il me fit de m'accorder un privilège qui n'est pas ordinaire, et qui étouffe avant leur naissance tous ces avortons illégitimes qui pourraient être engendrés d'ailleurs que de la légitime et nécessaire alliance de la théorie avec l'art"
  37. ↑ "...a useless piece, perfectly clean, polished and well filed on the outside but so imperfect inside that it is of no use whatsoever." translated from the French: "...qu'une pièce inutile, propre véritablement, polie et très bien limée par le dehors, mais tellement imparfaite au dedans qu'elle n'est d'aucun usage"
  38. ↑ All the quotes in this paragraph are found in (fr) Wikisource: Avis nécessaire à ceux qui auront curiosité de voir la Machine d'Arithmétique et de s'en servir.
  39. ↑ Picture of Burattini's machine Archived 9 June 2010 at the Wayback Machine Florence, Istituto e Museo di Storia della Scienza, inv. 3179 (accessed on January, 09 2012)
  40. ↑ 40.0 40.1 A calculator Chronicle, 300 years of counting and reckoning tools, p. 12, IBM
  41. ↑ Michael Williams, p.140 (1997)
  42. ↑ Picture of Morland multiplying machine Florence, Istituto e Museo di Storia della Scienza, inv. 679 (retrieved on January, 09 2012)
  43. ↑ They belong to the Musée des Arts et Métiers in Paris.
  44. ↑ "Grillet's machine doesn't even deserve the name of machine" translated from the French "La machine de Grillet ne mérite donc pas même le nom de machine", Jean Marguin, p.76 (1994)
  45. ↑ Copy of Poleni's machine (it) Museo Nazionale della Scienza e della Tecnologia Leonardo Da Vinci. Retrieved 4 October 2010
  46. ↑ Jean Marguin, p. 93-94 (1994)
  47. ↑ translated from the French: "De plus le report ne s'effectuant pas en cascade, la machine devait se bloquer au-delà de quelques reports simultanés", Jean Marguin, p.78 (1994)
  48. ↑ Jean Marguin, p.94-96 (1994)
  49. ↑ #MARG, Jean Marguin, pages 80–81 (1994)
  50. ↑ Marguin, p.83 (1994)
  51. ↑ Picture of Hahn's Calculator IBM Collection of mechanical calculators
  52. ↑ Jean Marguin, pages 84–86 (1994)
  53. ↑ Door E. Felt, p.15-16 (1916)
  54. ↑ "CNUM – 8KU54-2.5 : p.249 – im.253". cnum.cnam.fr.
  55. ↑ "History of Computers and Computing, Mechanical calculators, 19th century, Luiggi Torchi". history-computer.com. 4 January 2021.
  56. ↑ Roegel, Denis (2016). "Before Torchi and Schwilgué, There Was White". IEEE Annals of the History of Computing. 38 (4): 92–93. doi:10.1109/MAHC.2016.46.
  57. ↑ This is one third of the 120 years that this industry lasted
  58. ↑ "ववव.ारितमोमेट्रे.ऑर्ग". arithmometre.org. {{cite web}}: Check |url= value (help)
  59. ↑ Felt, Dorr E. (1916). यांत्रिक अंकगणित, या गिनती मशीन का इतिहास. Chicago: Washington Institute. p. 4.
  60. ↑ 60.0 60.1 "The calculating engines of English mathematician Charles Babbage (1791–1871) are among the most celebrated icons in the prehistory of computing. Babbage's Difference Engine No.1 was the first successful automatic calculator and remains one of the finest examples of precision engineering of the time. Babbage is sometimes referred to as "father of computing." The International Charles Babbage Society (later the Charles Babbage Institute) took his name to honor his intellectual contributions and their relation to modern computers." Charles Babbage Institute (page. Retrieved 1 February 2012).
  61. ↑ Ifrah G., The Universal History of Numbers, vol 3, page 127, The Harvill Press, 2000
  62. ↑ Chase G.C.: History of Mechanical Computing Machinery, Vol. 2, Number 3, July 1980, IEEE Annals of the History of Computing, p. 204
  63. ↑ Serial numbers and Years of manufacturing www.arithmometre.org, Valéry Monnier
  64. ↑ J.A.V. Turck, Origin of modern calculating machines, The Western Society of Engineers, 1921, p. 75
  65. ↑ 65.0 65.1 G. Trogemann, pages: 39–45
  66. ↑ David J. Shaw: The Cathedral Libraries Catalogue, The British Library and the Bibliographical Society, 1998
  67. ↑ J.A.V. Turck, Origin of modern calculating machines, The Western Society of Engineers, 1921, p. 143
  68. ↑ Wolff, John (30 May 2007). ""करोड़पति" गणना मशीन - तकनीकी विवरण". John Wolff's Web Museum. Retrieved 2019-12-30.
  69. ↑ James Essinger, p.76 (2004)
  70. ↑ "The better part of my live has now been spent on that machine, and no progress whatever having been made since 1834...", Charles Babbage, quoted in Irascible Genius, 1964, p.145
  71. ↑ "It is reasonable to inquire, therefore, whether it is possible to devise a machine which will do for mathematical computation what the automatic lathe has done for engineering. The first suggestion that such a machine could be made came more than a hundred years ago from the mathematician Charles Babbage. Babbage's ideas have only been properly appreciated in the last ten years, but we now realize that he understood clearly all the fundamental principles which are embodied in modern digital computers" B. V. Bowden, 1953, pp. 6,7
  72. ↑ Howard Aiken, 1937, reprinted in The origins of Digital computers, Selected Papers, Edited by Brian Randell, 1973
  73. ↑ NCR Retrospective website. Retrieved October, 02 2012
  74. ↑ History of the cash register. Retrieved October, 05 2012
  75. ↑ See the number of machines built in 1890 in this paragraph
  76. ↑ Dick and Joan's antique. Retrieved October, 02 2012
  77. ↑ List of serial numbers by dates arithmometre.org. Retrieved 10 October 2012
  78. ↑ Before the computer, James W. Cortada, p.34 ISBN 0-691-04807-X
  79. ↑ A notable difference was that the Millionaire calculator used an internal mechanical product lookup table versus a repeated addition or subtraction until a counter was decreased down to zero and stopped the machine for the arithmometer
  80. ↑ L'ami des Sciences 1856, p. 301 www.arithmometre.org (page. Retrieved 22 September 2010)
  81. ↑ Larousse, P. (1886), Grand dictionnaire universel du XIX siècle, Paris, entry for A-M Guerry
  82. ↑ Hook & Norman p.252 (2001): "Grant developed two models of his calculating machine: a Barrel model, which he exhibited at the Centennial Exposition along with his difference engine; and a Rack and Pinion model, of which he was able to sell 125 examples. Although Grant never made much money from his calculating machines, his experiences in designing and constructing them led him to establish the highly successful Grant Gear Works, which helped to pioneer the gear-cutting industry in the United States."
  83. ↑ "Improved Calculating Machine", "Scientific American" Vol. XXXVI, No. 19, 12 May 1877 p.294 New York: Munn &Company (Publisher)
  84. ↑ Patent application in French from www.ami19.org scanned by Valéry Monnier (retrieved on 12 January 2012)
  85. ↑ "The Twin Marchant".
  86. ↑ "John Wolff's Web Museum - Facit C1-13 - Technical Description".

स्रोत

बाहरी संबंध

Wikisource has the text of the 1911 Encyclopædia Britannica article "Calculating Machines".
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=यांत्रिक_कैलकुलेटर&oldid=239272’