पॉवरसेट निर्माण
गणना और ऑटोमेटा सिद्धांत के सिद्धांत में, पॉवरसेट निर्माण या सबसेट निर्माण एक [[गैर-नियतात्मक परिमित ऑटोमेटन]] (एनएफए) को एक नियतात्मक परिमित ऑटोमेटन (डीएफए) में परिवर्तित करने के लिए एक मानक विधि है जो समान औपचारिक भाषा को पहचानता है। यह सैद्धांतिक रूप से महत्वपूर्ण है क्योंकि यह स्थापित करता है कि एनएफए, अपने अतिरिक्त लचीलेपन के बावजूद, किसी भी भाषा को पहचानने में असमर्थ हैं जिसे कुछ डीएफए द्वारा मान्यता नहीं दी जा सकती है। निर्माण में आसान एनएफए को अधिक कुशलतापूर्वक निष्पादन योग्य डीएफए में परिवर्तित करना व्यवहार में भी महत्वपूर्ण है। हालाँकि, यदि एनएफए में एन राज्य हैं, तो परिणामी डीएफए में 2 तक हो सकते हैंn बताता है, एक तेजी से बड़ी संख्या, जो कभी-कभी बड़े एनएफए के लिए निर्माण को अव्यवहारिक बना देती है।
निर्माण, जिसे कभी-कभी अन्य प्रकार के ऑटोमेटा के समान निर्माणों से अलग करने के लिए 'राबिन-स्कॉट पावरसेट निर्माण' (या सबसेट निर्माण) कहा जाता है, पहली बार 1959 में माइकल ओ. राबिन और दाना स्कॉट द्वारा प्रकाशित किया गया था।[1]
अंतर्ज्ञान
किसी दिए गए इनपुट स्ट्रिंग पर डीएफए के संचालन को अनुकरण करने के लिए, किसी को किसी भी समय एक ही स्थिति पर नज़र रखने की आवश्यकता होती है: वह स्थिति जहां ऑटोमेटन इनपुट के सबस्ट्रिंग # उपसर्ग को देखने के बाद पहुंचेगा। इसके विपरीत, एनएफए का अनुकरण करने के लिए, किसी को राज्यों के एक सेट पर नज़र रखने की आवश्यकता होती है: ऑटोमेटन द्वारा बनाए गए गैर-नियतात्मक विकल्पों के अनुसार, सभी राज्य जहां ऑटोमेटन इनपुट के समान उपसर्ग को देखने के बाद पहुंच सकता है। यदि, इनपुट के एक निश्चित उपसर्ग के बाद, एक सेट S राज्यों तक पहुंचा जा सकता है, फिर अगले इनपुट प्रतीक के बाद x पहुंच योग्य राज्यों का सेट एक नियतात्मक कार्य है S और x. इसलिए, पहुंच योग्य एनएफए राज्यों के सेट एनएफए सिमुलेशन में वही भूमिका निभाते हैं जैसे एकल डीएफए राज्य डीएफए सिमुलेशन में निभाते हैं, और वास्तव में इस सिमुलेशन में दिखाई देने वाले एनएफए राज्यों के सेट को डीएफए के राज्यों के रूप में फिर से व्याख्या किया जा सकता है।[2]
निर्माण
पावरसेट निर्माण सबसे सीधे एनएफए पर लागू होता है जो इनपुट प्रतीकों (उर्फ: ε-मूव्स) का उपभोग किए बिना राज्य परिवर्तनों की अनुमति नहीं देता है। ऐसे ऑटोमेटन को टुपल|5-टपल के रूप में परिभाषित किया जा सकता है (Q, Σ, T, q0, F), जिसमें Q राज्यों का समूह है, Σ इनपुट प्रतीकों का सेट है, T संक्रमण फ़ंक्शन है (एक राज्य और एक इनपुट प्रतीक को राज्यों के समूह में मैप करना), q0 प्रारंभिक अवस्था है, और F स्वीकार करने वाले राज्यों का समूह है। संगत DFA में उपसमुच्चय के अनुरूप स्थितियाँ होती हैं Q. DFA की प्रारंभिक अवस्था है {q0}, प्रारंभिक अवस्थाओं का (एक-तत्व) सेट। डीएफए का संक्रमण कार्य किसी राज्य का मानचित्रण करता है S (के एक उपसमुच्चय का प्रतिनिधित्व करना Q) और एक इनपुट प्रतीक x सेट पर T(S,x) = ∪{T(q,x) | q ∈ S}, सभी राज्यों का समूह जिन तक a द्वारा पहुंचा जा सकता है x-एक राज्य से संक्रमण S. एक राज्य S डीएफए एक स्वीकार्य राज्य है यदि और केवल तभी जब इसका कम से कम एक सदस्य हो S एनएफए की एक स्वीकार्य स्थिति है।[2][3] पावरसेट निर्माण के सबसे सरल संस्करण में, डीएफए के सभी राज्यों का सेट सत्ता स्थापित है Q, के सभी संभावित उपसमुच्चय का समुच्चय Q. हालाँकि, परिणामी DFA की कई स्थितियाँ बेकार हो सकती हैं क्योंकि वे प्रारंभिक अवस्था से अप्राप्य हो सकती हैं। निर्माण का एक वैकल्पिक संस्करण केवल उन राज्यों का निर्माण करता है जो वास्तव में पहुंच योग्य हैं।[4]
एनएफए ε-चालों के साथ
ε-मूव्स (जिसे ε-NFA भी कहा जाता है) वाले एनएफए के लिए, राज्यों के ε-प्रतिवर्ती सकर्मक समापन की गणना करके इनसे निपटने के लिए निर्माण को संशोधित किया जाना चाहिए: केवल ε-मूव्स का उपयोग करके किसी दिए गए राज्य से पहुंचने योग्य सभी राज्यों का सेट। वैन नोर्ड पावरसेट निर्माण में इस क्लोजर गणना को शामिल करने के तीन संभावित तरीकों को पहचानते हैं:[5]
- प्रीप्रोसेसिंग चरण के रूप में संपूर्ण ऑटोमेटन के ε-क्लोजर की गणना करें, ε-चालों के बिना समतुल्य एनएफए का उत्पादन करें, फिर नियमित पावरसेट निर्माण लागू करें। इस संस्करण पर हॉपक्रॉफ्ट और उल्मैन ने भी चर्चा की,[6] लागू करना आसान है, लेकिन बड़ी संख्या में ε-मूव्स वाले ऑटोमेटा के लिए अव्यावहारिक है, जैसा कि आमतौर पर प्राकृतिक भाषा प्रसंस्करण अनुप्रयोग में होता है।[5]
- पावरसेट गणना के दौरान, ε-क्लोजर की गणना करें प्रत्येक राज्य का q जिसे एल्गोरिथम द्वारा माना जाता है (और परिणाम को कैश करें)।
- पावरसेट गणना के दौरान, ε-क्लोजर की गणना करें राज्यों के प्रत्येक उपसमूह का Q' जिसे एल्गोरिथम द्वारा माना जाता है, और इसके तत्वों को इसमें जोड़ा जाता है Q'.
एकाधिक प्रारंभिक अवस्थाएँ
यदि एनएफए को कई प्रारंभिक स्थितियों की अनुमति देने के लिए परिभाषित किया गया है,[7] संबंधित डीएफए की प्रारंभिक अवस्था एनएफए की सभी प्रारंभिक अवस्थाओं का समुच्चय है, या (यदि एनएफए में ε-चालें भी हैं) ε-चालों द्वारा प्रारंभिक अवस्थाओं तक पहुंचने योग्य सभी अवस्थाओं का समुच्चय है।
उदाहरण
नीचे दिए गए एनएफए में चार राज्य हैं; अवस्था 1 प्रारंभिक है, और अवस्था 3 और 4 स्वीकार कर रहे हैं। इसकी वर्णमाला में दो प्रतीक 0 और 1 शामिल हैं, और इसमें ε-चालें हैं।
इस एनएफए से निर्मित डीएफए की प्रारंभिक स्थिति उन सभी एनएफए राज्यों का सेट है जो ε-चालों द्वारा राज्य 1 से पहुंच योग्य हैं; अर्थात्, यह समुच्चय {1,2,3} है।
इनपुट प्रतीक 0 द्वारा {1,2,3} से संक्रमण को या तो राज्य 1 से राज्य 2 तक तीर का अनुसरण करना चाहिए, या राज्य 3 से राज्य 4 तक तीर का पालन करना चाहिए। इसके अतिरिक्त, न तो राज्य 2 और न ही राज्य 4 में आउटगोइंग ε-चालें हैं। इसलिए, T({1,2,3},0) = {2,4}, और इसी तर्क से एनएफए से निर्मित पूर्ण डीएफए नीचे दिखाया गया है।
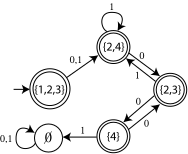जैसा कि इस उदाहरण में देखा जा सकता है, डीएफए की आरंभिक स्थिति से पांच राज्यों तक पहुंचा जा सकता है; एनएफए राज्यों के सेट के पावरसेट में शेष 11 सेट पहुंच योग्य नहीं हैं।
जटिलता
क्योंकि DFA राज्यों में NFA राज्यों के सेट शामिल होते हैं, a n-स्टेट एनएफए को अधिक से अधिक डीएफए में परिवर्तित किया जा सकता है 2n बताता है.[2]हरएक के लिए n, वहां है n-एनएफए को ऐसे बताएं कि राज्यों का प्रत्येक उपसमूह प्रारंभिक उपसमूह से पहुंच योग्य हो, ताकि परिवर्तित डीएफए बिल्कुल सही हो 2n बताता है, Θ(2n) सबसे खराब स्थिति जटिलता|सबसे खराब स्थिति समय जटिलता।[8][9] लगभग इतने राज्यों की आवश्यकता वाला एक सरल उदाहरण वर्णमाला {0,1} पर स्ट्रिंग की भाषा है जिसमें कम से कम हैं n अक्षर, द nजिनमें से अंतिम से वां 1 है। इसे a द्वारा दर्शाया जा सकता है (n + 1)-एनएफए बताएं, लेकिन इसकी आवश्यकता है 2n डीएफए बताता है, प्रत्येक के लिए एक n-इनपुट का वर्ण प्रत्यय; सी एफ के लिए चित्र n=4.[4]
अनुप्रयोग
डीएफए न्यूनीकरण#ब्रज़ोज़ोव्स्की का एल्गोरिदम|डीएफए न्यूनतमकरण के लिए ब्रज़ोज़ोव्स्की का एल्गोरिदम पावरसेट निर्माण का दो बार उपयोग करता है। यह अपने सभी तीरों को उलट कर और प्रारंभिक और स्वीकार करने वाले राज्यों की भूमिकाओं का आदान-प्रदान करके, रिवर्स भाषा के लिए इनपुट डीएफए को एनएफए में परिवर्तित करता है, पावरसेट निर्माण का उपयोग करके एनएफए को वापस डीएफए में परिवर्तित करता है, और फिर इसकी प्रक्रिया को दोहराता है। कुछ अन्य ज्ञात डीएफए न्यूनीकरण एल्गोरिदम के विपरीत, इसकी सबसे खराब स्थिति की जटिलता घातीय है, लेकिन कई उदाहरणों में यह अपनी सबसे खराब स्थिति की जटिलता की तुलना में अधिक तेजी से प्रदर्शन करती है।[10] सफरा का निर्माण, जो एक गैर-नियतात्मक बुची ऑटोमेटन को परिवर्तित करता है n एक नियतात्मक मुलर ऑटोमेटन में या 2 के साथ एक नियतात्मक ω-ऑटोमेटन में बताता हैहे(n लकड़ी का लट्ठा n) बताता है, पावरसेट निर्माण को अपनी मशीनरी के हिस्से के रूप में उपयोग करता है।[11]
संदर्भ
- ↑ Rabin, M. O.; Scott, D. (1959). "परिमित ऑटोमेटा और उनकी निर्णय समस्याएं". IBM Journal of Research and Development. 3 (2): 114–125. doi:10.1147/rd.32.0114. ISSN 0018-8646.
- ↑ 2.0 2.1 2.2 Sipser, Michael (1997). "Theorem 1.19". संगणना के सिद्धांत का परिचय. pp. 55–56. ISBN 0-534-94728-X.
- ↑ Hopcroft, John E.; Ullman, Jeffrey D. (1979). "The equivalence of DFA's and NFA's". Introduction to Automata Theory, Languages, and Computation. Reading Massachusetts: Addison-Wesley. pp. 22–23. ISBN 0-201-02988-X.
- ↑ 4.0 4.1 4.2 Schneider, Klaus (2004). Verification of reactive systems: formal methods and algorithms. Springer. pp. 210–212. ISBN 978-3-540-00296-3.
- ↑ 5.0 5.1 Van Noord, Gertjan (2000). "एप्सिलॉन का उपचार उपसमुच्चय निर्माण में चलता है". Computational Linguistics. 26 (1): 61–76. arXiv:cmp-lg/9804003. doi:10.1162/089120100561638. S2CID 5622079.
- ↑ Hopcroft & Ullman (1979), pp. 26–27.
- ↑ Rothe, Jörg (2006). Complexity Theory and Cryptology: An Introduction to Cryptocomplexity. Texts in Theoretical Computer Science. Springer. pp. 21–22. ISBN 9783540285205..
- ↑ Lupanov, Oleg B. (1963). "A comparison of two types of finite sources". Problemy Kibernetiki. 9: 321–326.
- ↑ Moore, Frank R. (1971). "On the bounds for state-set size in the proofs of equivalence between deterministic, nondeterministic, and two-way finite automata". IEEE Transactions on Computers. C-20 (10): 1211–1214. doi:10.1109/T-C.1971.223108. S2CID 206618275..
- ↑ Brzozowski, J. A. (1963). "Canonical regular expressions and minimal state graphs for definite events". Proc. Sympos. Math. Theory of Automata (New York, 1962). Polytechnic Press of Polytechnic Inst. of Brooklyn, Brooklyn, N.Y. pp. 529–561. MR 0175719.
- ↑ Safra, S. (1988). "On the complexity of ω-automata". Proceedings of the 29th Annual Symposium on Foundations of Computer Science (FOCS '88). Washington, DC, USA: IEEE Computer Society. pp. 319–327. doi:10.1109/SFCS.1988.21948..
अग्रिम पठन
- Anderson, James Andrew (2006). Automata theory with modern applications. Cambridge University Press. pp. 43–49. ISBN 978-0-521-84887-9.
