त्रिकोण तरंग
| त्रिकोण तरंग | |
|---|---|
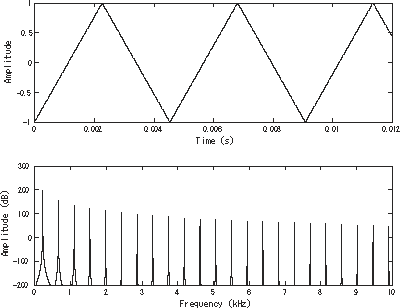 A बैंडलिमिटेड त्रिकोण तरंग[1] समय डोमेन (ऊपर) और आवृत्ति डोमेन (नीचे) में चित्रित मौलिक 220 Hz (A3) पर होता है। | |
| General information | |
| सामान्य परिभाषा | |
| आवेदन के क्षेत्र | इलेक्ट्रॉनिक्स, सिंथेसाइज़र |
| Domain, Codomain and Image | |
| डोमेन | |
| कोडोमेन | |
| Basic features | |
| समता | ओडीडी |
| अवधि | 1 |
| Specific features | |
| रूट | |
| व्युत्पन्न | वर्ग तरंग |
| फोरियर श्रेणी | |
त्रिकोण तरंग या त्रिकोणीय तरंग गैर-साइनसॉइडल तरंगरूप होता है जिसका नाम इसके त्रिभुज आकार के कारण रखा गया है। यह वास्तविक चर का आवधिक कार्य, टुकड़े-टुकड़े रैखिक कार्य, निरंतर वास्तविक कार्य होते है।
वर्गाकार तरंग की भांति, त्रिभुज तरंग में केवल विषम लयबद्ध होते हैं। चूँकि, उच्च हार्मोनिक्स वर्ग तरंग की तुलना में अधिक तेजी से लुढ़कता है (केवल व्युत्क्रम के विपरीत हार्मोनिक संख्या के व्युत्क्रम वर्ग के आनुपातिक)।
परिभाषाएँ
परिभाषा
अवधि पी की त्रिकोण तरंग जो सीमा [0,1] तक फैली हुई है, इसको इस प्रकार परिभाषित किया गया है।
सीमा में फैली त्रिभुज तरंग के लिए [−1,1] अभिव्यक्ति बन जाती है।
आयाम=5, आवर्त=4 के साथ त्रिभुज तरंग
चूँकि यह केवल मॉड्यूलो ऑपरेशन और निरपेक्ष मान का उपयोग करता है, इसका उपयोग हार्डवेयर इलेक्ट्रॉनिक्स पर त्रिकोण तरंग को क्रियान्वित करने के लिए किया जा सकता है।
ध्यान दीजिए कि अनेक प्रोग्रामिंग भाषाओं में, % ऑपरेटर शेष ऑपरेटर होता है (परिणाम लाभांश के समान चिह्न के साथ), मॉड्यूलो ऑपरेशन नहीं प्रोग्रामिंग भाषाओं में, मॉड्यूलो ऑपरेशन का उपयोग करके प्राप्त किया जा सकता है ((x % p) + p) % p की स्थान x % p. उदाहरण के लिए जावास्क्रिप्ट, इसका परिणाम फॉर्म का समीकरण होता है। 4*a/p * Math.abs((((x-p/4)%p)+p)%p - p/2) - a
वर्ग तरंग से संबंध
त्रिभुज तरंग को वर्ग तरंग के अभिन्न अंग के रूप में भी व्यक्त किया जा सकता है।
त्रिकोणमितीय फलनों में अभिव्यक्ति
अवधि पी और आयाम ए के साथ त्रिकोण तरंग को उन लोगों के और आर्कसीन के संदर्भ में व्यक्त किया जा सकता है (जिसका मान −π/2 से π/2 तक होता है)।
वैकल्पिक रैखिक कार्यों के रूप में व्यक्त
-1 से 1 तक की सीमा और अवधि पी के साथ त्रिकोण तरंग की और परिभाषा होती है।
हार्मोनिक्स

प्रत्येक अन्य विषम हार्मोनिक को -1 से गुणा करते हुए (या, समकक्ष, इसके चरण को परिवर्तित करते हुए) मौलिक के विषम हार्मोनिक्स को जोड़कर योगात्मक संश्लेषण के साथ त्रिकोण तरंग π का अनुमान लगाना संभव है) और हार्मोनिक्स के आयाम को उनके मोड संख्या के वर्ग से गुणा करके, n (जो मौलिक आवृत्ति के सापेक्ष उनकी आवृत्ति के वर्ग के सामान्तर होती है)।
उपरोक्त को गणितीय रूप से निम्नानुसार संक्षेपित किया जा सकता हैπ
यह अनंत फूरियर श्रृंखला तेजी से त्रिभुज तरंग में परिवर्तित हो जाती है N अनंत की ओर प्रवृत्त होता है, जैसा कि एनीमेशन में दिखाया गया है।
आर्क लंबाई
त्रिभुज तरंग के लिए प्रति आवर्त चाप की लंबाई, एस द्वारा निरूपित, आयाम ए और आवर्त लंबाई पी के संदर्भ में दी गई है।
यह भी देखें
- आवधिक कार्यों की सूची
- साइन लहर
- स्क्वेर तरंग
- सॉटूथ तरंग
- नाड़ी तरंग
- ध्वनि
- त्रिकोण फलन
- तरंग
- वक्र
संदर्भ
- ↑ Kraft, Sebastian; Zölzer, Udo (5 September 2017). "LP-BLIT: Bandlimited Impulse Train Synthesis of Lowpass-filtered Waveforms". Proceedings of the 20th International Conference on Digital Audio Effects (DAFx-17). 20th International Conference on Digital Audio Effects (DAFx-17). Edinburgh. pp. 255–259.

