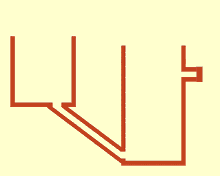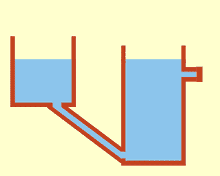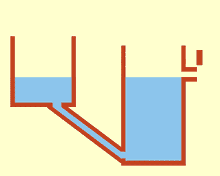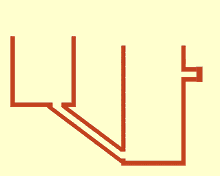
संचार वाहिकाएँ
संचार करने वाले बर्तन या फूलदान[1] कंटेनरों का एक सेट है जिसमें एक सजातीय तरल पदार्थ होता है और तरल के शीर्ष से काफी नीचे तक जुड़ा होता है: जब तरल जम जाता है, तो यह कंटेनरों के आकार और मात्रा की परवाह किए बिना सभी कंटेनरों में समान स्तर पर संतुलित हो जाता है। यदि एक बर्तन में अतिरिक्त तरल जोड़ा जाता है, तो तरल सभी जुड़े हुए बर्तनों में फिर से एक नया समान स्तर पा लेगा। इसकी खोज साइमन स्टीवन ने स्टीविन के नियम के परिणामस्वरूप की थी।[2] ऐसा इसलिए होता है क्योंकि प्रत्येक बर्तन में गुरुत्वाकर्षण और दबाव स्थिर होते हैं (Hydrostatic_paradox#Hydrostatic_pressure)।[3]
ब्लेस पास्कल ने सत्रहवीं शताब्दी में सिद्ध किया कि द्रव के अणु पर डाला गया दबाव सभी दिशाओं में पूर्ण और समान तीव्रता से प्रसारित होता है।
अनुप्रयोग
प्राचीन रोम के दिनों से, संचार वाहिकाओं की अवधारणा का उपयोग जलवाही स्तर और सीसा पाइप के माध्यम से इनडोर पाइपलाइन के लिए किया जाता रहा है। पानी सिस्टम के सभी हिस्सों में समान स्तर तक पहुंच जाएगा, जो संचार वाहिकाओं के रूप में कार्य करता है, भले ही पाइप का सबसे निचला बिंदु क्या हो - हालांकि व्यावहारिक रूप से सिस्टम का सबसे निचला बिंदु तरल के दबाव को झेलने के लिए पाइपलाइन की क्षमता पर निर्भर करता है।
शहरों में, जल टावरों का अक्सर उपयोग किया जाता है ताकि शहर की पाइपलाइन संचार वाहिकाओं के रूप में कार्य कर सके, जो पर्याप्त दबाव के साथ इमारतों की ऊंची मंजिलों तक पानी वितरित कर सके।
संचार वाहिकाओं की प्रणालियों का उपयोग करने वाले हाइड्रॉलिक प्रेस, औद्योगिक प्रक्रियाओं के विभिन्न अनुप्रयोगों में व्यापक रूप से उपयोग किए जाते हैं।
यह भी देखें
संदर्भ
- ↑ Mario Bunge, Philosophy of Science: From Explanation to Justification, 1998, ISBN 1412830834, p. 369
- ↑ Spellman, Frank R.; Whiting, Nancy E. (2005). Environmental engineer's mathematics handbook. CRC Press. ISBN 978-1-56670-681-0.
- ↑ Fontana, Fabrizio; DiCapua Roberto (August 2005). "Role of hydrostatic paradoxes towards the formation of the scientific thought of students at academic level". European Journal of Physics (6): 1017–1030. Bibcode:2005EJPh...26.1017F. doi:10.1088/0143-0807/26/6/009.