प्रवाह मानचित्र

चार्ल्स जोसेफ मिनार्ड रूस पर फ्रांसीसी आक्रमण का नक्शा (1812)।

प्रवाह मानचित्र एक प्रकार का विषयगत मानचित्र है जो गति को दर्शाने के लिए रैखिक मानचित्र प्रतीक का उपयोग करता है। इस प्रकार इसे मानचित्र और प्रवाह आरेख का एक संकर माना जा सकता है। नक्शा की जा रही गतिविधि किसी भी चीज़ की हो सकती है, जिसमें लोग, राजमार्ग यातायात, व्यापारिक सामान, पानी, विचार, दूरसंचार डेटा आदि शामिल हैं।^[1] चलती सामग्रियों की व्यापक विविधता, और उनके स्थानांतरण के माध्यम से भौगोलिक नेटवर्क की विविधता ने कई अलग-अलग डिज़ाइन रणनीतियों को जन्म दिया है। कुछ मानचित्रकारों ने इस शब्द का विस्तार परिवहन नेटवर्क के किसी भी विषयगत मानचित्र तक किया है, जबकि अन्य ने इसके उपयोग को उन मानचित्रों तक सीमित कर दिया है जो विशेष रूप से किसी प्रकार की गतिविधि दिखाते हैं।

कई प्रवाह मानचित्र प्रवाह की मात्रा के आनुपातिक रेखा की चौड़ाई का उपयोग करते हैं, जो उन्हें अन्य मानचित्रों के समान बनाता है जो आनुपातिक दृश्य चर का उपयोग करते हैं, जिसमें कार्टोग्राम (क्षेत्र क्षेत्र को बदलना), और आनुपातिक प्रतीक मानचित्र | आनुपातिक बिंदु प्रतीक शामिल हैं।

इतिहास

1838 में आयरलैंड में प्री-रेलरोड कार्गो यातायात का नक्शा, आनुपातिक प्रतीकों का उपयोग करने वाले पहले विषयगत मानचित्रों में से एक।

प्रवाह की मात्रा को दर्शाने वाला सबसे पहला ज्ञात मानचित्र इंजीनियर हेनरी ड्रुरी हार्नेस द्वारा 1838 में आयरलैंड में रेल परिवहन के इतिहास पर एक रिपोर्ट के हिस्से के रूप में प्रकाशित दो मानचित्र थे, जो सड़क और नहर द्वारा कार्गो यातायात की मात्रा दर्शाते थे।^[2]^[3] बाद के वर्षों में, अन्य लोगों ने यूरोप में इस तकनीक का प्रयोग किया, जब तक कि चार्ल्स जोसेफ मिनार्ड ने इसमें महारत हासिल नहीं कर ली।^[4]

1850 और 1860 के दशक के दौरान, मिनार्ड ने अपने कार्टेस आलंकारिकों के बीच विविध विषयों पर बयालीस प्रवाह मानचित्र प्रकाशित किए। इनमें उनका 1869 का रूस पर फ्रांसीसी आक्रमण (1812)|1812-1813 में रूस पर फ्रांसीसी आक्रमण का नक्शा भी शामिल है, जिसे अब तक तैयार किया गया सबसे अच्छा सांख्यिकीय ग्राफिक कहा गया है।^[5]^[6] मिनार्ड के कई मानचित्र डिज़ाइन तकनीकों का उपयोग करते हैं जिनमें कंप्यूटर ग्राफिक्स के युग में भी अभी तक सुधार नहीं किया गया है।

1980 के दशक के दौरान, वाल्डो आर. टॉबलर ने कंप्यूटर द्वारा प्रवाह मानचित्र बनाने के लिए प्रयोग किए।^[7]^[8] प्रारंभिक कंप्यूटर-जनित मानचित्र मिनार्ड मानकों के अनुरूप नहीं थे, लेकिन भौगोलिक सूचना प्रणाली (जीआईएस) और ग्राफ़िक्स सॉफ़्टवेयर ने प्रवाह मानचित्रों को डिजाइन करने की क्षमता में सुधार किया है।

प्रवाह परिघटना

1830 के दशक से विभिन्न प्रकार के प्रवाह मानचित्र बनाए गए हैं, जो कई रूपों में गति दर्शाते हैं। एडवर्ड इम्होफ़ ़ के अनुसार, एक प्रवाह मानचित्र उन घटनाओं के कई अलग-अलग पहलुओं का प्रतिनिधित्व कर सकता है जो आगे बढ़ रही हैं और जिस नेटवर्क के साथ वे चलती हैं; उन्होंने निम्नलिखित सूचीबद्ध किया:^[9]^: 94–95

उत्पत्ति और गंतव्य: कोई चीज कहां से कहां की ओर बढ़ रही है?
मार्ग: संचलन किस रेखा के साथ होता है? इसे सटीक, सामान्यीकृत या केवल सीधी रेखाओं के योजनाबद्ध रूप में दर्शाया जा सकता है^[10]
गति का प्रकार: क्या स्थानांतरित किया जाता है? इस नाममात्र श्रेणी में चर शामिल हो सकते हैं जैसे कि उत्पाद को एक बिंदु से दूसरे स्थान पर भेजा जाना, परिवहन का वाहन तरीका, या समुद्र की धारा में पानी का तापमान।
गतिविधि की मात्रा: कितना स्थानांतरित किया गया है? क्या परिवहन की गई वस्तु की मात्रा लगातार (धीरे-धीरे) या चरणों में बदल रही है? यह माप का एक गैर-नकारात्मक स्तर होगा, जैसे प्रति दिन वाहन, प्रवासियों की कुल संख्या, या प्रति सेकंड घन फीट में जल प्रवाह। कुछ प्रवाह मानचित्र वास्तविक गति मात्रा के बजाय प्रवाह क्षमता का प्रतिनिधित्व करते हैं, जैसे दूरसंचार बैंडविड्थ।
गति की दिशा: कोई चीज़ किस दिशा में, या दोनों दिशाओं में स्थानांतरित की जाती है? इसे अक्सर तीरों द्वारा दर्शाया जाता है।^[11]
प्रवाह वेग: कोई चीज़ किस गति से या कितने समय में चलती है? यह एक अनुपात चर है जो गति की मात्रा के समान है, लेकिन उससे भिन्न है। एक उदाहरण औसत वाहन गति, या हवा के वेग का उपयोग करके राजमार्ग यातायात स्तर का प्रतिनिधित्व करना होगा।

ये विशिष्ट प्रकार के मानचित्र नहीं हैं; एक प्रवाह मानचित्र इनमें से किसी भी पहलू को एक साथ चित्रित कर सकता है।

प्रवाह मानचित्रों का विषय रही घटनाओं के प्रकार विविध हैं। मानव भूगोल से संबंधित विषयों में शामिल हैं: मानव प्रवास, यात्रा, अंतर्राष्ट्रीय व्यापार, रसद, सार्वजनिक उपयोगिता (पानी, सीवर, बिजली, दूरसंचार), और यातायात, अन्य। अन्य भौतिक भूगोल से संबंधित हैं: पर्यावरणीय प्रवाह, हवा, पशु प्रवास, आदि।

प्रवाह मानचित्र के प्रकार

2014 तक सभी वाणिज्यिक यात्री एयरलाइन मार्गों का मूल-गंतव्य प्रवाह मानचित्र। चमकीला पीला हवाई मार्गों के उच्च घनत्व को दर्शाता है।

विषय वस्तु में प्रवाह मानचित्रों की भिन्नता और इम्होफ़ के प्रवाह के पहलुओं के सापेक्ष महत्व ने कई डिज़ाइन रणनीतियों को जन्म दिया है। 1987 की थीसिस में, मैरी पार्क्स ने कई अलग-अलग प्रकार के प्रवाह मानचित्रों की पहचान की,^[12] जिसे व्यापक रूप से उद्धृत किया गया है, हालांकि उसकी सूची व्यापक नहीं थी और यहां और अधिक शामिल हैं। ये प्रकार प्रोटोटाइपिक हैं; वास्तविक मानचित्र कई प्रकार के कुछ पहलुओं को जोड़ सकते हैं।

उत्पत्ति-गंतव्य मानचित्र

इस प्रकार में, प्राथमिक उद्देश्य दो स्थानों के बीच संबंध के अस्तित्व को दिखाना है, अक्सर प्रवाह की मात्रा और/या दिशा के प्रतिनिधित्व के साथ।^[11]मार्ग आम तौर पर दर्शकों के लिए महत्वपूर्ण नहीं होता है, इसलिए कनेक्टिंग लाइनें अक्सर सीधी या थोड़ी घुमावदार होती हैं। इस फॉर्म का एक सामान्य उदाहरण एयरलाइन रूट मैप है। पार्क ने रेडियल मानचित्रों (एकल मूल या गंतव्य से निकलने वाले) को नेटवर्क मानचित्रों (कई नोड्स को आपस में जोड़ने वाले) से अलग किया, लेकिन यह भौगोलिक पैटर्न में एक अंतर है; डिज़ाइन दोनों प्रकार के लिए बहुत समान है।

मूल-गंतव्य मानचित्रों में कनेक्टिंग लाइनों के योजनाबद्ध आकार पर एक अद्वितीय डिजाइन फोकस होता है। सीधी रेखाएँ खींचना आसान है, लेकिन समस्याएँ पैदा कर सकती हैं, खासकर जब लंबी रेखाएँ और छोटी रेखाएँ एकरेखीय हों, जो एक-दूसरे और उनके गंतव्यों को अस्पष्ट करती हों। उनका रूप भी बेतरतीब हो सकता है। इन कारणों से, घुमावदार रेखाएं, आमतौर पर गोलाकार चाप, सौंदर्य की दृष्टि से अधिक आकर्षक मानी जाती हैं। उनमें हस्तक्षेप करने वाली रेखाओं और बिंदुओं से बचने के लिए समायोजित करने की क्षमता भी होती है।^[13] आरंभिक स्वचालित लाइन जनरेशन एल्गोरिदम आम तौर पर सीधी रेखाएँ थे,^[8]लेकिन हाल के एल्गोरिदम घुमावदार रेखाएँ बनाने में सफल रहे हैं।^[14]

वितरण मानचित्र

छवि: मिनार्ड's map of French wine exports for 1864.jpg|thumb|300px|1864 के लिए चार्ल्स जोसेफ मिनार्ड का फ्रांसीसी शराब निर्यात के इतिहास का नक्शा, वितरण प्रवाह मानचित्र का एक प्रारंभिक उदाहरण। इस प्रकार को मूल-गंतव्य नोड्स, उनके बीच यात्रा के मार्गों (आमतौर पर अत्यधिक सामान्यीकृत), और प्रवाह की मात्रा पर संतुलित फोकस द्वारा उदाहरण दिया गया है। सबसे आम उदाहरण, मिनार्ड का, एक नक्शा है जो सामान्य समुद्री मार्गों के साथ-साथ नोड क्षेत्रों या बंदरगाह शहरों के एक समूह के बीच शिपिंग को दर्शाता है। वितरण मानचित्र में, पथ कई गंतव्यों की कुल चौड़ाई के समानुपाती चौड़ाई के साथ मूल से निकलते हैं, फिर प्रत्येक गंतव्य की ओर वितरित होने वाले मार्गों के रूप में विभाजित होते हैं।

वितरण मानचित्रों को डिज़ाइन करने के लिए प्रवाह रेखाओं को प्रारूपित करने में कुछ देखभाल और शिल्प की आवश्यकता होती है ताकि वे उचित चौड़ाई और चिकनी घुमावदार कोणों पर विभाजित हो जाएं। संगणना प्रयोगों ने इन्हें स्वचालित रूप से उत्पन्न करने की क्षमता दिखाई है,^[1]लेकिन आज अधिकांश जीआईएस और ग्राफिक्स सॉफ्टवेयर का उपयोग करके अर्ध-मैन्युअल रूप से तैयार किए जाते हैं।^[11]

नेटवर्क मार्ग मानचित्र

एक विशिष्ट योजनाबद्ध पारगमन मानचित्र नेटवर्क मार्ग मानचित्र का एक सरल रूप है, जिसमें अत्यधिक सामान्यीकृत पारगमन मार्गों पर ध्यान केंद्रित किया जाता है

इस प्रकार का प्रवाह मानचित्र मूल रूप से आयरलैंड के हार्नेस मानचित्र का है।^[3]यह नेटवर्क के मूल/गंतव्य नोड्स की तुलना में उसके मार्गों पर अधिक ध्यान केंद्रित करता है। मार्ग सटीक या अत्यधिक सामान्यीकृत हो सकते हैं (जैसा कि कई पारगमन मानचित्रों में होता है), और प्रवाह की मात्रा या गति का प्रतिनिधित्व कर भी सकते हैं और नहीं भी। एक सामान्य उदाहरण ट्रैफ़िक भीड़ मानचित्र है।

सतत/द्रव्यमान प्रवाह मानचित्र

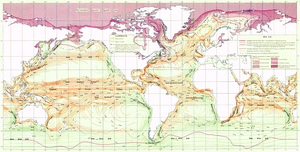
स्ट्रीमलाइन तकनीक का उपयोग करके समुद्री धाराओं का 1943 का मानचित्र। गर्म और ठंडी धाराओं में अंतर करने के लिए रंग के उपयोग पर ध्यान दें।

सभी प्रवाह रैखिक नेटवर्क के साथ नहीं होते हैं; द्वि- और त्रि-आयामी द्रव्यमान भी प्रवाहित हो सकते हैं, विशेष रूप से पानी (जैसे, समुद्री धारा) और वायु (पवन)। उनके आंदोलन को एक वेक्टर क्षेत्र के रूप में मॉडल किया जा सकता है, जिसमें अंतरिक्ष में किसी भी बिंदु पर आंदोलन की परिमाण और दिशा को मापा जा सकता है।^[9]^: 149 उपरोक्त इम्होफ़ की सूची में, एक मानचित्र जो इसकी कल्पना करता है, जिसे अक्सर द्रव्यमान प्रवाह मानचित्र या सतत प्रवाह मानचित्र कहा जाता है,^[15] प्रवाह की दिशा और गति पर ध्यान केंद्रित करता है, जबकि उत्पत्ति/गंतव्य और यात्रा का मार्ग जैसे अन्य पहलू काफी हद तक अर्थहीन हैं।

1688 में, एडमंड हैली ने वायु प्रवाह की दिशा में उन्मुख छोटी रेखा खंडों की एक श्रृंखला का उपयोग करके व्यापारिक हवाओं का मानचित्रण किया।^[4]^: 69 20वीं सदी के शुरुआती मौसम मानचित्रों में, इस तकनीक को पवन बार्ब्स में विस्तृत किया गया था, हवा की गति के साथ-साथ दिशा को इंगित करने के लिए जटिल प्रतीकों का उपयोग किया जाता था। यूनिट वैक्टर और स्ट्रीमलेट्स को बिंदु-आधारित प्रवाह प्रतीकों के लिए एक सामान्य शब्द के रूप में प्रस्तावित किया गया है, लेकिन इनमें से कोई भी व्यापक उपयोग में नहीं है।^[16] इन्हें कंप्यूटर एल्गोरिदम द्वारा आसानी से उत्पन्न किया जा सकता है, विशेष रूप से रेखापुंज ग्राफिक्स जीआईएस डेटा या नमूना बिंदु डेटा (जैसे, मौसम स्टेशन) का उपयोग करके।^[17] यह दृष्टिकोण सामान्य प्रवाह मानचित्र की तुलना में आनुपातिक प्रतीक मानचित्र के अधिक समान है।

वेक्टर फ़ील्ड के लिए एक अन्य विज़ुअलाइज़ेशन विकल्प स्ट्रीमलाइन बनाना है, जो उन बिंदुओं को जोड़ता है जो एक दूसरे में प्रवाहित होंगे; इसका उपयोग आमतौर पर 19वीं सदी की शुरुआत से समुद्री धाराओं को दर्शाने के लिए किया जाता रहा है।^[4]^: 82 वाल्डो आर. टोबलर|टोबलर के 1981 के कंप्यूटर एल्गोरिदम स्ट्रीकलाइन उत्पन्न करने के लिए वेक्टर फ़ील्ड के मॉडल थे, और बाद के काम से परिणामों में सुधार हुआ है।^[7]^[16]

वज़न स्केलिंग

प्रवाह की मात्रा या गति की कल्पना करने की सबसे आम तकनीक आकार के दृश्य चर के माध्यम से है, विशेष रूप से लाइन वजन (आमतौर पर प्वाइंट (टाइपोग्राफी) या मिलीमीटर में मापा जाता है)। जैसा कि कहा गया है, कुल राशि के लिए आकार बहुत अधिक सहज है, इसलिए गति के लिए अन्य दृश्य चर (जैसे ह्यू या लपट ) पर भी विचार किया जा सकता है। रेखा भार निर्धारित करने की निम्नलिखित विधियाँ आनुपातिक प्रतीक मानचित्रों के लिए स्केलिंग विधियों के समान हैं।^[11]

मनमाने ढंग से चयनित वजन w के आधार पर, राशि मान v के सीधे अनुपात में किसी दी गई रेखा w के वजन की गणना करना सबसे आम तरीका है।₀ चयनित आधार मान के लिए v₀ (अक्सर लेकिन जरूरी नहीं कि न्यूनतम मूल्य):

${\frac {w}{w_{0}}}={\frac {v}{v_{0}}}$ इससे पाठकों को सापेक्ष भार के आधार पर सापेक्ष मूल्य अनुपात के बारे में सहज निर्णय लेने में मदद मिलती है; एक रेखा जो दूसरी से दोगुनी मोटी है, दोगुने मान का प्रतिनिधित्व करती है। हालाँकि, जब उच्चतम और निम्नतम मूल्यों (आम तौर पर, 25:1 से अधिक, हालांकि यह प्रवाह नेटवर्क और डिज़ाइन के भूगोल पर निर्भर करता है) के बीच बहुत उच्च स्तर का अंतर होता है, तो परिणामी मानचित्र अत्यधिक मोटी रेखाओं और लगभग अदृश्य पतली रेखाओं के साथ समस्याग्रस्त हो सकता है। इस मामले में एक विकल्प न्यूनतम और अधिकतम वजन (जैसे) निर्धारित करना है_max और डब्ल्यू_min) और उनके बीच रैखिक प्रक्षेप करें, भले ही यह वजन अनुपात को सहज रूप से आंकने की क्षमता को समाप्त कर देता है: ${\frac {w-w_{min}}{w_{max}-w_{min}}}={\frac {v-v_{min}}{v_{max}-v_{min}}}$ तीसरा विकल्प एक क्रमिक चर या एक मात्रात्मक चर का प्रतिनिधित्व करने के लिए क्रमिक भार (मोटा, मध्यम, पतला, आदि) का उपयोग करना है जिसे वर्गीकृत किया गया है (अक्सर इस संदर्भ में रेंज ग्रेडिंग कहा जाता है)। इससे पाठकों की मूल्य अंतरों को सहजता से आंकने की क्षमता भी ख़त्म हो जाती है, लेकिन समग्र सरलता का लाभ मिलता है।

इन सभी प्रकार की स्केलिंग के लिए, लेजेंड आमतौर पर आनुपातिक प्रतीक मानचित्र की लेजेंड के समान, उनके संबंधित मूल्यों के साथ लाइन वेट का एक नमूना सेट दिखाता है।

अन्य प्रकार के प्रवाह आरेख

एक गैर-कार्टोग्राफ़िक प्रवाह मानचित्र जो प्रमुख अंग प्रणालियों को वितरित कार्डियक आउटपुट के सापेक्ष प्रतिशत को दर्शाता है

मानचित्रकला में प्रवाह मानचित्रों के अलावा गैर-भौगोलिक प्रवाह को देखने के लिए कई अन्य विधियाँ भी हैं:

द्रव प्रवाह का बेकर प्रवाह मानचित्र
रक्त प्रवाह मानचित्र, न्यूरोइमेजिंग का इतिहास देखें
प्रवाह मानचित्र या समाधान ऑपरेटर, यादृच्छिक गतिशील प्रणाली देखें
विनिर्माण प्रक्रिया का प्रक्रिया प्रवाह मानचित्र
सैंके आरेख
एक्सएसएल प्रवाह मानचित्र, एक्सएसएल फ़ॉर्मेटिंग ऑब्जेक्ट देखें

यह भी देखें

प्रवाह आरेख (बहुविकल्पी)
विषयगत मानचित्र

संदर्भ

↑ ^1.0 ^1.1 Phan, Doantam; Xiao, Ling; Yeh, Ron; Hanrahan, Pat; Winograd, Terry (2005). "Flow map layout". IEEE Symposium on Information Visualization, 2005. INFOVIS 2005. pp. 219–224. doi:10.1109/INFVIS.2005.1532150. ISBN 0-7803-9464-X.
↑ Robinson, Arthur H. (Dec 1955). "The 1837 Maps of Henry Drury Harness". The Geographical Journal. 121 (4): 440–450. doi:10.2307/1791753. JSTOR 1791753.
↑ ^3.0 ^3.1 Griffith, Richard John; Harness, Henry Drury (1838). Atlas to Accompany 2nd Report of the Railway Commissioners. Ireland.
↑ ^4.0 ^4.1 ^4.2 Robinson, Arthur H. (1982). कार्टोग्राफी के इतिहास में प्रारंभिक विषयगत मानचित्रण. University of Chicago Press. pp. 147–154.
↑ Tufte, Edward (2006). सुंदर साक्ष्य. Graphics Press. Bibcode:2006beev.book.....T.
↑ Jacobs, Frank. "मिनार्ड मानचित्र - "अब तक का सबसे अच्छा सांख्यिकीय ग्राफ़िक"". Big Think. Retrieved 13 November 2020.
↑ ^7.0 ^7.1 Tobler, Waldo R. (January 1981). "भौगोलिक आंदोलन का एक मॉडल". Geographical Analysis. 13 (1): 1–20. doi:10.1111/j.1538-4632.1981.tb00711.x.
↑ ^8.0 ^8.1 Tobler, Waldo R. (1987). "कंप्यूटर द्वारा माइग्रेशन मैपिंग में प्रयोग". The American Cartographer. 14 (2): 155–163. doi:10.1559/152304087783875273. S2CID 1363699.
↑ ^9.0 ^9.1 Imhof, Eduard (1972). विषयगत मानचित्रण. Berlin: De Gruyter.
↑ Robinson, Arthur H., Elements of Cartography, 2nd Edition, New York: Wiley, 1960.
↑ ^11.0 ^11.1 ^11.2 ^11.3 Dent, Borden D.; Torguson, Jeffrey S.; Hodler, Thomas W. (2009). Cartography: Thematic Map Design (6th ed.). McGraw-Hill. pp. 188–201.
↑ Parks, Mary J. (1987). American flow mapping: A survey of the flow maps found in twentieth century geography textbooks, including a classification of the various flow map designs. Georgia State University: Unpublished M.A. thesis.
↑ Jenny, Bernhard; Stephen, Daniel M.; Muehlenhaus, Ian; Marston, Brook E.; Sharma, Ritesh; Zhang, Eugene; Jenny, Helen (2018). "उत्पत्ति-गंतव्य प्रवाह मानचित्रों के लिए डिज़ाइन सिद्धांत". Cartography and Geographic Information Science. 45 (1): 62–75. doi:10.1080/15230406.2016.1262280. S2CID 36668445.
↑ Jenny, Bernhard; Stephen, Daniel M.; Muehlenhaus, Ian; Marston, Brooke E.; Sharma, Ritesh; Zhang, Eugene; Jenny, Helen (2017). "उद्गम-गंतव्य प्रवाह मानचित्रों का बल-निर्देशित लेआउट". International Journal of Geographical Information Science. 31 (8): 1521–1540. doi:10.1080/13658816.2017.1307378. S2CID 205794904.
↑ T. Slocum, R. McMaster, F. Kessler, H. Howard (2009). Thematic Cartography and Geovisualization, Third Edn, page 252. Pearson Prentice Hall: Upper Saddle River, NJ., pp.360-369.
↑ ^16.0 ^16.1 Turk, G.; Banks, D. (August 1996). "छवि-निर्देशित सुव्यवस्थित प्लेसमेंट". SIGGRAPH '96: Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques: 453–460. doi:10.1145/237170.237285. ISBN 0897917464. S2CID 2310527.
↑ Lavin, S.J.; Cerveny, R.S. (1987). "यूनिट-वेक्टर घनत्व मानचित्रण". The Cartographic Journal. 24 (2): 131–141. doi:10.1179/caj.1987.24.2.131.

बाहरी संबंध

[phan-1] 1.0 ^1.1 Phan, Doantam; Xiao, Ling; Yeh, Ron; Hanrahan, Pat; Winograd, Terry (2005). "Flow map layout". IEEE Symposium on Information Visualization, 2005. INFOVIS 2005. pp. 219–224. doi:10.1109/INFVIS.2005.1532150. ISBN 0-7803-9464-X.

[robinson1955-2] Robinson, Arthur H. (Dec 1955). "The 1837 Maps of Henry Drury Harness". The Geographical Journal. 121 (4): 440–450. doi:10.2307/1791753. JSTOR 1791753.

[harness1837-3] 3.0 ^3.1 Griffith, Richard John; Harness, Henry Drury (1838). Atlas to Accompany 2nd Report of the Railway Commissioners. Ireland.

[robinson1982-4] 4.0 ^4.1 ^4.2 Robinson, Arthur H. (1982). कार्टोग्राफी के इतिहास में प्रारंभिक विषयगत मानचित्रण. University of Chicago Press. pp. 147–154.

[tufte2006-5] Tufte, Edward (2006). सुंदर साक्ष्य. Graphics Press. Bibcode:2006beev.book.....T.

[jacobs-6] Jacobs, Frank. "मिनार्ड मानचित्र - "अब तक का सबसे अच्छा सांख्यिकीय ग्राफ़िक"". Big Think. Retrieved 13 November 2020.

[tobler1981-7] 7.0 ^7.1 Tobler, Waldo R. (January 1981). "भौगोलिक आंदोलन का एक मॉडल". Geographical Analysis. 13 (1): 1–20. doi:10.1111/j.1538-4632.1981.tb00711.x.

[tobler1987-8] 8.0 ^8.1 Tobler, Waldo R. (1987). "कंप्यूटर द्वारा माइग्रेशन मैपिंग में प्रयोग". The American Cartographer. 14 (2): 155–163. doi:10.1559/152304087783875273. S2CID 1363699.

[imhof1972-9] 9.0 ^9.1 Imhof, Eduard (1972). विषयगत मानचित्रण. Berlin: De Gruyter.

[robinson1960-10] Robinson, Arthur H., Elements of Cartography, 2nd Edition, New York: Wiley, 1960.

[torguson2009-11] 11.0 ^11.1 ^11.2 ^11.3 Dent, Borden D.; Torguson, Jeffrey S.; Hodler, Thomas W. (2009). Cartography: Thematic Map Design (6th ed.). McGraw-Hill. pp. 188–201.

[parks1987-12] Parks, Mary J. (1987). American flow mapping: A survey of the flow maps found in twentieth century geography textbooks, including a classification of the various flow map designs. Georgia State University: Unpublished M.A. thesis.

[jenny2018-13] Jenny, Bernhard; Stephen, Daniel M.; Muehlenhaus, Ian; Marston, Brook E.; Sharma, Ritesh; Zhang, Eugene; Jenny, Helen (2018). "उत्पत्ति-गंतव्य प्रवाह मानचित्रों के लिए डिज़ाइन सिद्धांत". Cartography and Geographic Information Science. 45 (1): 62–75. doi:10.1080/15230406.2016.1262280. S2CID 36668445.

[jenny2017-14] Jenny, Bernhard; Stephen, Daniel M.; Muehlenhaus, Ian; Marston, Brooke E.; Sharma, Ritesh; Zhang, Eugene; Jenny, Helen (2017). "उद्गम-गंतव्य प्रवाह मानचित्रों का बल-निर्देशित लेआउट". International Journal of Geographical Information Science. 31 (8): 1521–1540. doi:10.1080/13658816.2017.1307378. S2CID 205794904.

[slocum2009-15] T. Slocum, R. McMaster, F. Kessler, H. Howard (2009). Thematic Cartography and Geovisualization, Third Edn, page 252. Pearson Prentice Hall: Upper Saddle River, NJ., pp.360-369.

[turk1996-16] 16.0 ^16.1 Turk, G.; Banks, D. (August 1996). "छवि-निर्देशित सुव्यवस्थित प्लेसमेंट". SIGGRAPH '96: Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques: 453–460. doi:10.1145/237170.237285. ISBN 0897917464. S2CID 2310527.

[17] Lavin, S.J.; Cerveny, R.S. (1987). "यूनिट-वेक्टर घनत्व मानचित्रण". The Cartographic Journal. 24 (2): 131–141. doi:10.1179/caj.1987.24.2.131.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

Anonymous

Search

प्रवाह मानचित्र

Namespaces

More

Page actions

Contents

इतिहास

प्रवाह परिघटना