अनुमस्तिष्क मॉडल आर्टिक्यूलेशन नियंत्रक

एकल जोड़ के लिए सीएमएसी प्रणाली का ब्लॉक आरेख। वेक्टर S को सभी जोड़ों के इनपुट के रूप में प्रस्तुत किया गया है। प्रत्येक जोड़ अलग से एक S -> A* मैपिंग और एक संयुक्त एक्चुएटर सिग्नल pi की गणना करता है। सभी जोड़ों के लिए समायोज्य वजन एक ही भौतिक मेमोरी में मौजूद हो सकते हैं।

अनुमस्तिष्क मॉडल अंकगणित कंप्यूटर (सीएमएसी) स्तनधारी सेरिबैलम के एक मॉडल पर आधारित एक प्रकार का तंत्रिका नेटवर्क है। इसे अनुमस्तिष्क मॉडल आर्टिक्यूलेशन नियंत्रक के रूप में भी जाना जाता है। यह एक प्रकार की एसोसिएशन (मनोविज्ञान) याद है।

सीएमएसी को पहली बार 1975 में जेम्स एल्बस द्वारा रोबोटिक नियंत्रकों के लिए एक फ़ंक्शन मॉडलर के रूप में प्रस्तावित किया गया था(इसलिए नाम), लेकिन इसका उपयोग सुदृढीकरण सीखने और यंत्र अधिगम समुदाय में स्वचालित वर्गीकरण के लिए भी बड़े पैमाने पर किया गया है। सीएमएसी परसेप्ट्रॉन मॉडल का विस्तार है। यह एक फ़ंक्शन की गणना करता है $n$ इनपुट आयाम. इनपुट स्पेस को हाइपर-आयतों में विभाजित किया गया है, जिनमें से प्रत्येक एक मेमोरी सेल से जुड़ा हुआ है। मेमोरी कोशिकाओं की सामग्री वजन है, जिसे प्रशिक्षण के दौरान समायोजित किया जाता है। आमतौर पर, इनपुट स्पेस के एक से अधिक परिमाणीकरण का उपयोग किया जाता है, ताकि इनपुट स्पेस में कोई भी बिंदु कई हाइपर-आयतों के साथ जुड़ा हो, और इसलिए कई मेमोरी कोशिकाओं के साथ जुड़ा हो। सीएमएसी का आउटपुट इनपुट बिंदु द्वारा सक्रिय सभी मेमोरी कोशिकाओं में वजन का बीजगणितीय योग है।

इनपुट बिंदु के मूल्य में परिवर्तन के परिणामस्वरूप सक्रिय हाइपर-आयत के सेट में परिवर्तन होता है, और इसलिए सीएमएसी आउटपुट में भाग लेने वाले मेमोरी कोशिकाओं के सेट में परिवर्तन होता है। इसलिए CMAC आउटपुट को एक वितरित तरीके से संग्रहीत किया जाता है, जैसे कि इनपुट स्पेस में किसी भी बिंदु से संबंधित आउटपुट कई मेमोरी कोशिकाओं में संग्रहीत मूल्य से प्राप्त होता है (इसलिए नाम एसोसिएटिव मेमोरी)। यह सामान्यीकरण प्रदान करता है।

बिल्डिंग ब्लॉक्स

सीएमएसी, 2डी स्पेस के रूप में दर्शाया गया है

निकटवर्ती छवि में, CMAC में दो इनपुट हैं, जिन्हें 2D स्थान के रूप में दर्शाया गया है। इस स्थान को दो अतिव्यापी ग्रिडों (एक को भारी रेखाओं में दिखाया गया है) के साथ विभाजित करने के लिए दो परिमाणीकरण कार्यों का उपयोग किया गया है। मध्य के पास एक एकल इनपुट दिखाया गया है, और इसने छायांकित क्षेत्र के अनुरूप दो मेमोरी सेल सक्रिय कर दिए हैं। यदि कोई अन्य बिंदु दिखाए गए बिंदु के करीब होता है, तो यह सामान्यीकरण प्रदान करते हुए कुछ समान मेमोरी कोशिकाओं को साझा करेगा।

सीएमएसी को इनपुट बिंदुओं और आउटपुट मानों के जोड़े प्रस्तुत करके और आउटपुट पर देखी गई त्रुटि के अनुपात के आधार पर सक्रिय कोशिकाओं में वजन समायोजित करके प्रशिक्षित किया जाता है। इस सरल प्रशिक्षण एल्गोरिदम में अभिसरण का प्रमाण है। हाइपर-आयत में कर्नेल फ़ंक्शन जोड़ना सामान्य है, ताकि हाइपर-आयत के किनारे की ओर गिरने वाले बिंदुओं में केंद्र के पास गिरने वाले बिंदुओं की तुलना में कम सक्रियता हो। सीएमएसी के व्यावहारिक उपयोग में उद्धृत प्रमुख समस्याओं में से एक आवश्यक मेमोरी आकार है, जो सीधे उपयोग की जाने वाली कोशिकाओं की संख्या से संबंधित है। इसे आमतौर पर हैश फंकशन का उपयोग करके सुधारा जाता है, और केवल वास्तविक कोशिकाओं के लिए मेमोरी स्टोरेज प्रदान किया जाता है जो इनपुट द्वारा सक्रिय होते हैं।

एक-चरण अभिसरण एल्गोरिथ्म

सीएमएसी के भार को अद्यतन करने के लिए प्रारंभ में न्यूनतम माध्य वर्ग (एलएमएस) पद्धति का उपयोग किया जाता है। सीएमएसी के प्रशिक्षण के लिए एलएमएस का उपयोग करने का अभिसरण सीखने की दर के प्रति संवेदनशील है और इससे विचलन हो सकता है। 2004 में, सीएमएसी को ऑनलाइन प्रशिक्षित करने के लिए एक पुनरावर्ती न्यूनतम वर्ग (आरएलएस) एल्गोरिदम पेश किया गया था। इसमें सीखने की दर को समायोजित करने की आवश्यकता नहीं है। इसका अभिसरण सैद्धांतिक रूप से सिद्ध हो चुका है और एक चरण में अभिसरण की गारंटी दी जा सकती है। इस आरएलएस एल्गोरिदम की कम्प्यूटेशनल जटिलता O(N3) है।

सीएमएसी तंत्रिका नेटवर्क की समानांतर पाइपलाइन संरचना

Left पैनल: वास्तविक कार्य; दायां पैनल: डेरिवेटिव के साथ CMAC सन्निकटन

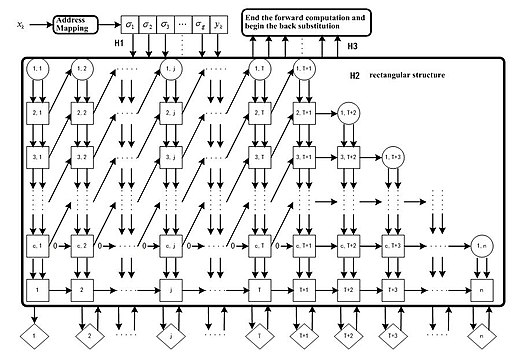
हार्डवेयर कार्यान्वयन अवसंरचना

क्यूआर अपघटन के आधार पर, एक एल्गोरिदम (क्यूआरएलएस) को ओ (एन) जटिलता के लिए और अधिक सरल बनाया गया है। नतीजतन, यह मेमोरी उपयोग और समय लागत को काफी कम कर देता है। इस एल्गोरिदम को लागू करने पर एक समानांतर पाइपलाइन सरणी संरचना पेश की गई है। कुल मिलाकर क्यूआरएलएस एल्गोरिथ्म का उपयोग करके, सीएमएसी तंत्रिका नेटवर्क अभिसरण की गारंटी दी जा सकती है, और प्रशिक्षण के एक चरण का उपयोग करके नोड्स के वजन को अद्यतन किया जा सकता है। इसकी समानांतर पाइपलाइन सरणी संरचना बड़े पैमाने पर उद्योग के उपयोग के लिए हार्डवेयर में लागू होने की बड़ी क्षमता प्रदान करती है।

सतत सीएमएसी

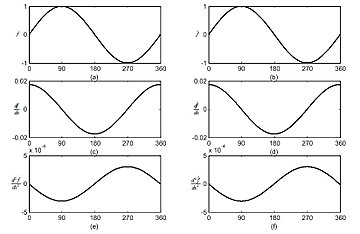
चूंकि सीएमएसी ग्रहणशील क्षेत्र कार्यों का आयताकार आकार बी-स्प्लिन कार्यों के साथ सीएमएसी को एकीकृत करके असंतत सीढ़ी फ़ंक्शन सन्निकटन का उत्पादन करता है, निरंतर सीएमएसी अनुमानित कार्यों के डेरिवेटिव के किसी भी क्रम को प्राप्त करने की क्षमता प्रदान करता है।

डीप सीएमएसी

हाल के वर्षों में, कई अध्ययनों ने पुष्टि की है कि कई उथली संरचनाओं को एक ही गहरी संरचना में रखकर, समग्र प्रणाली बेहतर डेटा प्रतिनिधित्व प्राप्त कर सकती है, और इस प्रकार, गैर-रेखीय और उच्च जटिलता कार्यों से अधिक प्रभावी ढंग से निपट सकती है। 2018 में, एक गहन सीएमएसी (डीसीएमएसी) ढांचा प्रस्तावित किया गया था और डीसीएमएसी मापदंडों का अनुमान लगाने के लिए एक बैकप्रॉपैगेशन एल्गोरिदम तैयार किया गया था। अनुकूली शोर रद्दीकरण कार्य के प्रायोगिक परिणामों से पता चला कि पारंपरिक सिंगल-लेयर सीएमएसी की तुलना में प्रस्तावित डीसीएमएसी बेहतर शोर रद्दीकरण प्रदर्शन प्राप्त कर सकता है।

सारांश

Scalability	Straightforward to extend to millions of neurons or further
Convergence	The training can always converge in one step
Function derivatives	Straightforward to obtain by employing B-splines interpolation
Hardware structure	Parallel pipeline structure
Memory usage	Linear with respect to the number of neurons
Computational complexity	O(N)

यह भी देखें

• Artificial neural network
• Recursive least squares filter
• Deep learning

अग्रिम पठन

• Albus, J.S. (1971). "Theory of Cerebellar Function". In: Mathematical Biosciences, Volume 10, Numbers 1/2, February 1971, pgs. 25–61
• Albus, J.S. (1975). "New Approach to Manipulator Control: The Cerebellar Model Articulation Controller (CMAC)". In: Transactions of the ASME Journal of Dynamic Systems, Measurement, and Control, September 1975, pgs. 220 – 227
• Albus, J.S. (1979). "Mechanisms of Planning and Problem Solving in the Brain". In: Mathematical Biosciences 45, pgs 247–293, 1979.
• Iwan, L., and Stengel, R., "The Application of Neural Networks to Fuel Processors for Fuel Cells" In IEEE Transactions on Vehicular Technology, Vol. 50 (1), pp. 125-143, 2001.
• Tsao, Y. (2018). "Adaptive Noise Cancellation Using Deep Cerebellar Model Articulation Controller". In: IEEE Access 6, April 2018, pgs 37395-37402.

बाहरी संबंध

• Blog on Cerebellar Model Articulation Controller (CMAC) by Ting Qin. More details on the one-step convergent algorithm, code development, etc.