शुल्ज़-ज़िम्म वितरण

Schulz–Zimm

Probability density function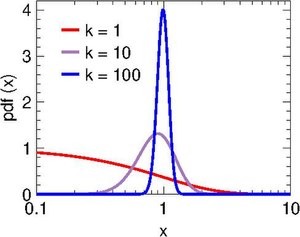
Parameters	$k$ (shape parameter)
Support	$x\in \mathbb {R} _{>0}$
PDF	${\frac {k^{k}x^{k-1}e^{-kx}}{\Gamma (k)}}$
Mean	$1$
Variance	${\frac {1}{k}}$

शुल्ज़-ज़िम्म वितरण गामा वितरण का एक विशेष कारक है। पॉलीमर की बहुविक्षेपणता को मॉडल करने के लिए इसका व्यापक रूप से उपयोग किया जाता है। इस संदर्भ में, इसे वर्ष1939 में गुंटर विक्टर शुल्ज़ द्वारा और वर्ष 1948 में ब्रूनो एच. ज़िम द्वारा पेश किया गया था।

इस वितरण में केवल एक आकार पैरामीटर k है, स्केल θ=1/k पर तय किया गया है। तदनुसार, संभाव्यता घनत्व फलन है

$$f(x)={\frac {k^{k}x^{k-1}e^{-kx}}{\Gamma (k)}}.$$

जब पॉलिमर पर लागू किया जाता है, तो चर x सापेक्ष द्रव्यमान या श्रृंखला की लंबाई होती है $x=M/M_{n}$. तदनुसार, वृहत पैमाने पर वितरण $f(M)$ स्केल पैरामीटर के साथ सिर्फ एक गामा वितरण है $\theta =M_{n}/k$. यह बताता है कि क्यों शुल्ज़-ज़िम्म वितरण अपने पारंपरिक अनुप्रयोग डोमेन के बाहर असाधारण है।

वितरण का माध्य 1 और विचरण 1/k है। पॉलिमर प्रसार है $\langle x^{2}\rangle /\langle x\rangle =1+1/k$.

वृहत k के लिए शुल्ज़-ज़िम्म वितरण गाऊसी वितरण के निकट पहुंचता है। एल्गोरिदम में जहां किसी को नमूने वर्णन करने की आवश्यकता होती है $x\geq 0$, शुल्ज़-ज़िम वितरण को गॉसियन की तुलना में प्राथमिकता दी जानी चाहिए क्योंकि बाद वाले को ऋणात्मक x को रोकने के लिए स्वेच्छा से कट-ऑफ की आवश्यकता होती है।