मोड़ (कोण)

From Vigyanwiki
Revision as of 10:36, 15 September 2023 by Neeraja (talk | contribs) (Neeraja moved page वर्तन (कोण) to मोड़ (कोण) without leaving a redirect)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

Turn
की इकाईPlane angle
चिन्ह, प्रतीकtr or pla
Conversions
1 tr in ...... is equal to ...
   radians   2π rad
≈ 6.283185307... rad
   milliradians   2000π mrad
≈ 6283.185307... mrad
   degrees   360°
   gradians   400g
केंद्र बिंदु के बारे में वामावर्त घुमाव जहां एक पूर्णघुमाव 1 मोड़ के घूर्णन के कोण से मेल खाता है।

एक मोड़ 2π रेडियन, 360 डिग्री या 400 ग्रेडियन के बराबर समतल कोण माप की एक इकाई है। इसके उपविभागों में अर्ध-मोड़, चौथाई-मोड़, सेंटीटर्न, मिलीटर्न आदि सम्मिलित हैं।

निकट संबंधी शब्द चक्र और क्रांति एक मोड़ के बराबर नहीं हैं।

उपखंड

एक मोड़ को 100 सेंटीटर्न या 1000 मिलीटर्न में विभाजित किया जा सकता है, जिसमें प्रत्येक मिलीटर्न 0.36° के कोण के अनुरूप होता है, जिसे 21′ 36″ के रूप में भी लिखा जा सकता है।[1] [2] सेंटीटर्न में विभाजित एक चांदा सामान्यतः एक "प्रतिशत कोणमापक" कहलाता है।

टर्न के बाइनरी अंशों का भी उपयोग किया जाता है। नाविकों ने पारंपरिक रूप से एक मोड़ को 32 कम्पास बिंदुओं में विभाजित किया है, जिसमें निहित रूप से 1/32 मोड़ का कोणीय पृथक्करण है। बाइनरी डिग्री, जिसे बाइनरी रेडियन (या ब्रैड) के रूप में भी जाना जाता है, है 1/256 मोड़। [3] बाइनरी डिग्री का उपयोग कंप्यूटिंग में किया जाता है ताकि एक बाइट में अधिकतम संभव सटीकता के लिए एक कोण का प्रतिनिधित्व किया जा सके। कंप्यूटिंग में उपयोग किए जाने वाले कोण के अन्य माप n के अन्य मानों के लिए एक पूरे मोड़ को 2n बराबर भागों में विभाजित करने पर आधारित हो सकते हैं। [4]

टर्न की धारणा सामान्यतः समतल कोण के लिए उपयोग की जाती है।

इतिहास

शब्द टर्न लैटिन और फ्रेंच के माध्यम से ग्रीक शब्द τόρνος (टॉर्नोस- एक खराद) से उत्पन्न हुआ है ।

1697 में, डेविड ग्रेगोरी ने इस्तेमाल किया π/ρ (पाई ओवर रो) एक वृत्त की परिधि को उसकी त्रिज्या से विभाजित करने के लिए निरूपित करने के लिए। [5] [6] यद्यपि, इससे पहले 1647 में, विलियम ऑट्रेड ने इस्तेमाल किया था δ/π (डेल्टा ओवर पाई) परिधि के व्यास के अनुपात के लिए। 1706 में वेल्श गणितज्ञ विलियम जोन्स द्वारा अपने वर्तमान अर्थ (व्यास द्वारा विभाजित परिधि) के साथ प्रतीक π का ​​पहला प्रयोग किया गया था। [7] यूलर ने 1737 में उस अर्थ के साथ प्रतीक को अपनाया, जिससे इसका व्यापक उपयोग हुआ।

टर्न के लिए लैटिन शब्द वर्सोर है, जो त्रि-आयामी अंतरिक्ष में एक मनमाने अक्ष के बारे में रोटेशन का प्रतिनिधित्व करता है। वर्सर्स अण्डाकार अंतरिक्ष में अंक बनाते हैं और 1840 के दशक में डब्ल्यूआर हैमिल्टन द्वारा विकसित एक बीजगणित, चतुष्कोणों के अध्ययन को प्रेरित करते हैं।

1922 से प्रतिशत चांदा मौजूद हैं, [8] लेकिन 1962 में ब्रिटिश खगोलशास्त्री फ्रेड हॉयल द्वारा सेंटीटर्न्स, मिलीटर्न्स और माइक्रोटर्न्स का प्रारम्भ बहुत बाद में किया गया था। [1] [2] तोपखाने और उपग्रह देखने के लिए कुछ माप उपकरणों में मिलीटर्न स्केल होते हैं। [9] [10]


इकाई प्रतीक

जर्मन मानक डीआईएन 1315 (मार्च 1974) ने घुमावों के लिए इकाई प्रतीक "पीएलए" (लैटिन से: plenus angulus 'पूर्ण कोण') प्रस्तावित किया। [11] [12] डीआईएन 1301-1 [डी] (अक्टूबर 2010) में सम्मिलित, तथाकथित वोलविंकल ('पूर्ण कोण') एक एसआई इकाई नहीं है। तथापि, यह यूरोपीय संघ [13] [14] और स्विट्जरलैंड में माप की एक कानूनी इकाई है। [15]

वैज्ञानिक कैलकुलेटर HP 39gII और HP प्राइम क्रमशः 2011 और 2013 से घुमावों के लिए इकाई प्रतीक "tr" का समर्थन करते हैं। 2016 में HP 50g के लिए नएRPL में "tr" के लिए समर्थन भी जोड़ा गया था, और 2017 में hp 39g+, HP 49g+, HP 39gs, और HP 40gs के लिए भी जोड़ा गया था। [16] [17] WP 43S के लिए भी एक कोणीय मोड टर्न का सुझाव दिया गया था, [18] लेकिन कैलकुलेटर इसके बजाय "MULπ" (π के गुणक) को 2019 से मोड और इकाई के रूप में लागू करता है। [19] [20]


इकाई रूपांतरण

इकाई वृत्त (जिसका त्रिज्या एक है) की परिधि 2π है।
डिग्री और रेडियन में व्यक्त कोणों की तुलना।

एक फेरा 2π (≈ 6.283185307179586) [21] रेडियन, 360 डिग्री, या 400 ग्रेडियन के बराबर है।

सामान्य कोणों का रूपांतरण
टर्न रेडियन डिग्री ग्रेडियन
0 turn 0 rad 0° 0g
1/24 turn 𝜏/24 rad[lower-alpha 1] π/12 rad 15° 16+2/3g
1/16 turn 𝜏/16 rad π/8 rad 22.5° 25g
1/12 turn 𝜏/12 rad π/6 rad 30° 33+1/3g
1/10 turn 𝜏/10 rad π/5 rad 36° 40g
1/8 turn 𝜏/8 rad π/4 rad 45° 50g
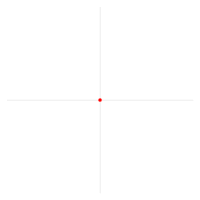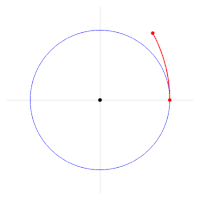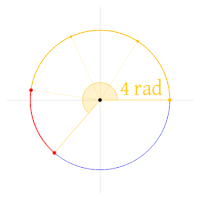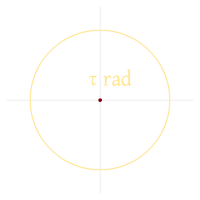
1/2π turn 1 rad c. 57.3° c. 63.7g
1/6 turn 𝜏/6 rad π/3 rad 60° 66+2/3g
1/5 turn 𝜏/5 rad 2π/5 rad 72° 80g
1/4 turn 𝜏/4 rad π/2 rad 90° 100g
1/3 turn 𝜏/3 rad 2π/3 rad 120° 133+1/3g
2/5 turn 2𝜏/5 rad 4π/5 rad 144° 160g
1/2 turn 𝜏/2 rad π rad 180° 200g
3/4 turn 3𝜏/4 rad 3π/2 rad 270° 300g
1 turn 𝜏 rad 2π rad 360° 400g
  1. ↑ In this table, 𝜏 [[Turn_(angle)#Proposals_for_a_single_letter_to_represent_2π|denotes 2π]].




2π को दर्शाने के लिए एक अक्षर का प्रस्ताव

इन्हें भी देखें: Pi § प्रतीक π को अपनाना

उस वृत्त की त्रिज्या के समान लंबाई वाला एक वृत्त का चाप 1 रेडियन के कोण से मेल खाता है। एक पूर्ण चक्र एक पूर्ण मोड़ या लगभग 6.28 रेडियन से मेल खाता है, जिसे यहां ग्रीक अक्षर ताऊ (τ) का उपयोग करके व्यक्त किया गया है।

1746 में, लियोनार्ड यूलर ने पहली बार एक वृत्त की त्रिज्या से विभाजित परिधि को दर्शाने के लिए ग्रीक अक्षर पाई का उपयोग किया था (अर्थात, π = 6.28...)। [22]

2001 में, रॉबर्ट पैलैस ने गणित को सरल और अधिक सहज ज्ञान युक्त बनाने के लिए, π के बजाय मूलभूत वृत्त स्थिरांक के रूप में रेडियन की संख्या का उपयोग करने का प्रस्ताव दिया, जो आधे चक्कर में रेडियन की संख्या के बराबर है। उनके प्रस्ताव स्थिरांक को दर्शाने के लिए "तीन टांगों वाला π" चिन्ह का प्रयोग किया गया था ()।[23]

2008 में, थॉमस कॉलिग्नाटस ने 2π का प्रतिनिधित्व करने के लिए अपरकेस ग्रीक अक्षर थीटा, θ प्रस्तावित किया [24]

ग्रीक अक्षर थीटा फोनीशियन और हिब्रू अक्षर टेथ, 𐤈 या ט से निकला है, और यह देखा गया है कि प्रतीक का पुराना संस्करण, जिसका अर्थ है पहिया, चार तीलियों वाले एक पहिया जैसा दिखता है। [25] 2π मात्रा का प्रतिनिधित्व करने के लिए पहिया प्रतीक, टेथ का उपयोग करने का भी प्रस्ताव दिया गया है, और हाल ही में पहिया, सूर्य, वृत्त या डिस्क प्रतीक के अस्तित्व पर अन्य प्राचीन संस्कृतियों के बीच एक संबंध बनाया गया है - अर्थात टेथ की अन्य विविधताएं - 2π के प्रतिनिधित्व के रूप में। [26]

2010 में, माइकल हार्टल ने वृत्त स्थिरांक का प्रतिनिधित्व करने के लिए ग्रीक अक्षर ताऊ का उपयोग करने का प्रस्ताव दिया: τ = 2π। उसने दो कारण बताए, प्रथम, τ एक मोड़ में रेडियंस की संख्या है, जो एक मोड़ के अंशों को अधिक सीधे व्यक्त करने की अनुमति देता है: उदाहरण के लिए, एक 3/4 मोड़ के रूप में दर्शाया जाएगा 3τ/4 के बजाय रेड 3π/2 रेड। दूसरा, τ दृष्टिगत रूप से π जैसा दिखता है, जिसका वृत्त स्थिरांक के साथ जुड़ाव अपरिहार्य है। [27] हार्टल का ताऊ मेनिफेस्टो [28] सूत्रों के कई उदाहरण देता है जो स्पष्ट होने का दावा करते हैं π के बजाय τ का उपयोग किया जाता है। [29] [30] [31]

प्रारंभ में, इन प्रबंधकों में से किसी को भी संबद्ध और वैज्ञानिक समुदाय द्वारा व्यापक स्वीकृति नहीं मिली। [32] तथापि, τ का उपयोग अधिक व्यापक हो गया है, [33] उदाहरण के लिए:

  • 2012 में, शैक्षिक वेबसाइट खान अकादमी ने τ के संदर्भ में व्यक्त किए गए उत्तरों को स्वीकार करना प्रारम्भ किया। [34]
  • इसका उपयोग कम से कम एक गणितीय शोध लेख में भी किया गया है, [44] जिसे τ-प्रमोटर पीटर हैरेमोएस ने लिखा है। [45]

निम्न तालिका दर्शाती है कि यदि τ = 2π का उपयोग π के बजाय किया जाता है तो विभिन्न पहचान कैसे दिखाई देती हैं। [46] [23] अधिक संपूर्ण सूची के लिए, π से जुड़े सूत्रों की सूची देखें।

सूत्र π का प्रयोग करना τ का प्रयोग करना टिप्पणियाँ
द्वारा घटाया गया कोण 1/4 एक वृत्त का π/2 रेड τ/4 रेड τ/4 रेड = 1/4 मोड़
त्रिज्या r के एक वृत्त की परिधि C C = 2πr C = τr
एक वृत्त का क्षेत्रफल A = πr2 A = τr2/2 θ कोण वाले त्रिज्यखंड का क्षेत्रफल A = θr2/2 है
इकाई परिधि के साथ एक नियमित एन-गॉन का क्षेत्रफल A = n/2 sin 2π/n A = n/2 sin τ/n
एन-बॉल और एन-स्फेयर वॉल्यूम पुनरावृत्ति संबंध V0(r) = 1

S0(r) = 2

कॉची का अभिन्न सूत्र
मानक सामान्य वितरण
स्टर्लिंग का अनुमान
यूलर की पहचान 0       eiπ = − 1
eiπ + 1 = 0 		0     eiτ = 1
eiτ − 1 = 0
एकता की जड़ें
प्लैंक स्थिरांक h घटा हुआ प्लैंक स्थिरांक है
कोणीय आवृत्ति







उपयोग के उदाहरण

  • एक कोणीय इकाई के रूप में, मोड़ कई अनुप्रयोगों में विशेष रूप से उपयोगी होता है, जैसे कि विद्युत चुम्बकीय कॉइल और घूर्णन वस्तुओं के संबंध में। घुमावदार संख्या भी देखें।
  • पाई चार्ट एक पूरे के अनुपात को एक मोड़ के अंशों के रूप में दर्शाते हैं। प्रत्येक एक प्रतिशत को एक सेंटीटर्न के कोण के रूप में दिखाया जाता है। [8]


यह भी देखें

संदर्भ

  1. ↑ 1.0 1.1 Hoyle, Fred (1962). Chandler, M. H. (ed.). Astronomy (1 ed.). London, UK: Macdonald. LCCN 62065943. OCLC 7419446. (320 pages)
  2. ↑ 2.0 2.1 Klein, Herbert Arthur (2012) [1988, 1974]. "Chapter 8: Keeping Track of Time". The Science of Measurement: A Historical Survey (The World of Measurements: Masterpieces, Mysteries and Muddles of Metrology). Dover Books on Mathematics (corrected reprint of original ed.). Dover Publications, Inc. / Courier Corporation (originally by Simon & Schuster, Inc.). p. 102. ISBN 978-0-48614497-9. LCCN 88-25858. Retrieved 6 August 2019. (736 pages)
  3. ↑ "ooPIC Programmer's Guide - Chapter 15: URCP". ooPIC Manual & Technical Specifications - ooPIC Compiler Ver 6.0. Savage Innovations, LLC. 2007 [1997]. Archived from the original on 28 June 2008. Retrieved 5 August 2019.
  4. ↑ Hargreaves, Shawn [in polski]. "Angles, integers, and modulo arithmetic". blogs.msdn.com. Archived from the original on 30 June 2019. Retrieved 5 August 2019.
  5. ↑ Beckmann, Petr (1989) [1970]. A History of Pi. Barnes & Noble Publishing.
  6. ↑ Schwartzman, Steven (1994). The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. The Mathematical Association of America. p. 165. ISBN 978-0-88385511-9.
  7. ↑ Veling, Anne (2001). "Pi through the ages". veling.nl. Archived from the original on 2 July 2009.
  8. ↑ 8.0 8.1 Croxton, Frederick E. (1922). "A Percentage Protractor - Designed for Use in the Construction of Circle Charts or "Pie Diagrams"". Journal of the American Statistical Association. Short Note. 18 (137): 108–109. doi:10.1080/01621459.1922.10502455.
  9. ↑ Schiffner, Friedrich (1965). "Bestimmung von Satellitenbahnen". Mitteilungen der Uraniasternwarte (in Deutsch). Wien.
  10. ↑ Hayes, Eugene Nelson (1975) [1968]. Trackers of the Skies. History of the Smithsonian Satellite-tracking Program. Cambridge, Massachusetts, USA: Academic Press / Howard A. Doyle Publishing Company.
  11. ↑ German, Sigmar; Drath, Peter (13 March 2013) [1979]. Handbuch SI-Einheiten: Definition, Realisierung, Bewahrung und Weitergabe der SI-Einheiten, Grundlagen der Präzisionsmeßtechnik (in Deutsch) (1 ed.). Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, reprint: Springer-Verlag. p. 421. ISBN 978-3-32283606-9. 978-3-528-08441-7, 978-3-32283606-9. Retrieved 14 August 2015.
  12. ↑ Kurzweil, Peter (9 March 2013) [1999]. Das Vieweg Einheiten-Lexikon: Formeln und Begriffe aus Physik, Chemie und Technik (in Deutsch) (1 ed.). Vieweg, reprint: Springer-Verlag. p. 403. doi:10.1007/978-3-322-92920-4. ISBN 978-3-32292920-4. 978-3-322-92921-1. Retrieved 14 August 2015.
  13. ↑ "Richtlinie 80/181/EWG - Richtlinie des Rates vom 20. Dezember 1979 zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Meßwesen und zur Aufhebung der Richtlinie 71/354/EWG" (in Deutsch). 15 February 1980. Archived from the original on 22 June 2019. Retrieved 6 August 2019.
  14. ↑ "Richtlinie 2009/3/EG des Europäischen Parlaments und des Rates vom 11. März 2009 zur Änderung der Richtlinie 80/181/EWG des Rates zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Messwesen (Text von Bedeutung für den EWR)" (in Deutsch). 11 March 2009. Archived from the original on 6 August 2019. Retrieved 6 August 2019.
  15. ↑ "Art. 15 Einheiten in Form von nichtdezimalen Vielfachen oder Teilen von SI-Einheiten". Einheitenverordnung. 23 November 1994. 941.202. Archived from the original on 10 May 2019. Retrieved 1 January 2013. {{cite book}}: |work= ignored (help)
  16. ↑ Lapilli, Claudio Daniel (11 May 2016). "RE: newRPL: Handling of units". HP Museum. Archived from the original on 10 August 2017. Retrieved 5 August 2019.
  17. ↑ Lapilli, Claudio Daniel (25 October 2018). "Chapter 3: Units - Available Units - Angles". newRPL User Manual. Archived from the original on 6 August 2019. Retrieved 7 August 2019. {{cite book}}: |work= ignored (help)
  18. ↑ Paul, Matthias R. (12 January 2016) [2016-01-11]. "RE: WP-32S in 2016?". HP Museum. Archived from the original on 5 August 2019. Retrieved 5 August 2019. [...] I'd like to see a TURN mode being implemented as well. TURN mode works exactly like DEG, RAD and GRAD (including having a full set of angle unit conversion functions like on the WP 34S), except for that a full circle doesn't equal 360 degree, 6.2831... rad or 400 gon, but 1 turn. (I […] found it to be really convenient in engineering/programming, where you often have to convert to/from other unit representations […] But I think it can also be useful for educational purposes. [...] Having the angle of a full circle normalized to 1 allows for easier conversions to/from a whole bunch of other angle units […]
  19. ↑ Bonin, Walter (2019) [2015]. WP 43S Owner's Manual (PDF). 0.12 (draft ed.). pp. 72, 118–119, 311. ISBN 978-1-72950098-9. Retrieved 5 August 2019. [1] [2] (314 pages)
  20. ↑ Bonin, Walter (2019) [2015]. WP 43S Reference Manual (PDF). 0.12 (draft ed.). pp. iii, 54, 97, 128, 144, 193, 195. ISBN 978-1-72950106-1. Retrieved 5 August 2019. [3] [4] (271 pages)
  21. ↑ Sequence OEIS: A019692
  22. ↑ Euler, L. (1746). Nova theoria lucis et colorum. Opuscula varii argumenti, p. 169–244.
  23. ↑ 23.0 23.1 Palais, Robert (2001). "Pi is Wrong" (PDF). The Mathematical Intelligencer. New York, USA: Springer-Verlag. 23 (3): 7–8. doi:10.1007/bf03026846. S2CID 120965049. Archived (PDF) from the original on 18 July 2019. Retrieved 5 August 2019.
  24. ↑ Colignatus, Th., "Trig rerigged. Trigonometry reconsidered. Measuring angles in 'unit meter around' and using the unit radius functions Xur and Yur". 2008-04-08, Legacy:COTP.
  25. ↑ Mann, S., Janzen, R., Ali, M. A., Scourboutakos, P., & Guleria, N. (October 2014). Integral kinematics (time-integrals of distance, energy, etc.) and integral kinesiology. In Proceedings of the 2014 IEEE GEM, Toronto, ON, Canada (pp. 22–24)
  26. ↑ Mann, S., Defaz, D., Pierce, C., Lam, D., Stairs, J., Hermandez, J., ... & Mann, C. (June 2019). Keynote-Eye Itself as a Camera: Sensors, Integrity, and Trust. In The 5th ACM Workshop on Wearable Systems and Applications (pp. 1–2).
  27. ↑ Hartl, Michael (14 March 2019) [2010-03-14]. "The Tau Manifesto". Archived from the original on 28 June 2019. Retrieved 14 September 2013.
  28. ↑ Hartl, Michael (14 March 2010). "The Tau Manifesto" (PDF). Archived (PDF) from the original on 18 July 2019. Retrieved 5 August 2019.
  29. ↑ Aron, Jacob (8 January 2011). "Michael Hartl: It's time to kill off pi". New Scientist. Interview. 209 (2794): 23. Bibcode:2011NewSc.209...23A. doi:10.1016/S0262-4079(11)60036-5.
  30. ↑ Landau, Elizabeth (14 March 2011). "On Pi Day, is 'pi' under attack?". cnn.com. CNN. Archived from the original on 19 December 2018. Retrieved 5 August 2019.
  31. ↑ Bartholomew, Randyn Charles (25 June 2014). "Let's Use Tau--It's Easier Than Pi - A growing movement argues that killing pi would make mathematics simpler, easier and even more beautiful". Scientific American. Archived from the original on 18 June 2019. Retrieved 20 March 2015.
  32. ↑ "Life of pi in no danger – Experts cold-shoulder campaign to replace with tau". Telegraph India. 30 June 2011. Archived from the original on 13 July 2013. Retrieved 5 August 2019.
  33. ↑ McMillan, Robert (13 March 2020). "For Math Fans, Nothing Can Spoil Pi Day—Except Maybe Tau Day". Wall Street Journal (in English). ISSN 0099-9660. Retrieved 21 May 2020.
  34. ↑ "Happy Tau Day!". blog.khanacademy.org (in English). Retrieved 19 December 2020.
  35. ↑ Coghlan, Nick (25 February 2017). "PEP 628 -- Add math.tau". Python.org. Archived from the original on 22 July 2019. Retrieved 5 August 2019.
  36. ↑ "math — Mathematical functions". Python 3.7.0 documentation. Archived from the original on 29 July 2019. Retrieved 5 August 2019.
  37. ↑ "Perl 6 terms". Archived from the original on 22 July 2019. Retrieved 5 August 2019.
  38. ↑ "TAU". Processing. Archived from the original on 22 July 2019. Retrieved 5 August 2019.
  39. ↑ "math". Nim. Archived from the original on 22 July 2019. Retrieved 5 August 2019.
  40. ↑ "std::f64::consts::TAU - Rust". doc.rust-lang.org. Retrieved 9 October 2020.
  41. ↑ Darcy, Joe. "JDK-8283136: Add constant for tau to Math and StrictMath". bugs.openjdk.org.
  42. ↑ John-H-K. "Add Math.Tau Pull Request #37517 · dotnet/Runtime". GitHub.
  43. ↑ "tau: Tau, the ratio between any circle's circumference and radius". Retrieved 6 December 2022.
  44. ↑ Harremoës, Peter (2017). "Bounds on tail probabilities for negative binomial distributions". Kybernetika. 52 (6): 943–966. arXiv:1601.05179. doi:10.14736/kyb-2016-6-0943. S2CID 119126029.
  45. ↑ Harremoës, Peter (17 November 2018). "Al-Kashi's constant τ" (PDF). Archived (PDF) from the original on 22 July 2019. Retrieved 20 September 2018.
  46. ↑ Abbott, Stephen (April 2012). "My Conversion to Tauism" (PDF). Math Horizons. 19 (4): 34. doi:10.4169/mathhorizons.19.4.34. S2CID 126179022. Archived (PDF) from the original on 28 September 2013.


बाहरी कड़ियाँ

Retrieved from ‘https://www.vigyanwiki.in/index.php?title=मोड़_(कोण)&oldid=258131’