बंडल मानचित्र

गणित में, एक बंडल मैप (या बंडल आकारिता ) फाइबर बंडलों की श्रेणी (गणित) में एक मॉर्फिज्म है। बंडल मैप की दो अलग, लेकिन बारीकी से संबंधित धारणाएं हैं, जो इस बात पर निर्भर करती हैं कि प्रश्न में फाइबर बंडलों में एक सामान्य फाइबर बंडल है या नहीं। मूल विषय पर भी कई भिन्नताएँ हैं, जो इस पर निर्भर करता है कि फ़ाइबर बंडलों की कौन सी श्रेणी विचाराधीन है। पहले तीन खंडों में, हम टोपोलॉजिकल स्पेस की श्रेणी में सामान्य फाइबर बंडलों पर विचार करेंगे। फिर चौथे भाग में कुछ अन्य उदाहरण दिये जायेंगे।

मानचित्रों को एक सामान्य आधार पर बंडल करें

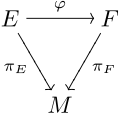
होने देना $\pi _{E}\colon E\to M$ और $\pi _{F}\colon F\to M$ एक स्थान एम पर फाइबर बंडल बनें। फिर 'ई से एफ ओवर एम तक बंडल मैप' एक सतत मानचित्र है $\varphi \colon E\to F$ ऐसा है कि $\pi _{F}\circ \varphi =\pi _{E}$. यानी डायग्राम

क्रमविनिमेय आरेख होना चाहिए। समान रूप से, M में किसी भी बिंदु x के लिए, $\varphi$ फाइबर को मैप करता है $E_{x}=\pi _{E}^{-1}(\{x\})$ फ़ाइबर से x के ऊपर E का $F_{x}=\pi _{F}^{-1}(\{x\})$ F के ऊपर x का.

फाइबर बंडलों की सामान्य आकृतियाँ

चलो π_E:E→ M और π_F:F→ N क्रमशः रिक्त स्थान M और N पर फाइबर बंडल बनें। फिर एक सतत मानचित्र $\varphi :E\to F$ ई से एफ तक एक बंडल मानचित्र कहा जाता है यदि कोई सतत मानचित्र एफ:एम→ एन ऐसा हो कि आरेख

आवागमन, अर्थात्, $\pi _{F}\circ \varphi =f\circ \pi _{E}$. दूसरे शब्दों में, $\varphi$ फाइबर-संरक्षण है, और एफ ई के फाइबर के स्थान पर प्रेरित मानचित्र है: चूंकि π_E विशेषण है, f विशिष्ट रूप से निर्धारित होता है $\varphi$. किसी दिए गए f के लिए, ऐसा बंडल मानचित्र $\varphi$ कहा जाता है कि यह एक बंडल मैप कवरिंग एफ है।

दो धारणाओं के बीच संबंध

परिभाषाओं से यह तुरंत पता चलता है कि एम पर एक बंडल मैप (पहले अर्थ में) एम के पहचान मानचित्र को कवर करने वाले बंडल मैप के समान है।

इसके विपरीत, पुलबैक बंडल की धारणा का उपयोग करके सामान्य बंडल मानचित्रों को एक निश्चित आधार स्थान पर बंडल मानचित्रों में कम किया जा सकता है। यदि π_F:F→ N, N के ऊपर एक फाइबर बंडल है और f:M→ N एक सतत मानचित्र है, तो F द्वारा F का 'पुलबैक' एक फाइबर बंडल f है^*M के ऊपर F जिसका x के ऊपर का फाइबर (f) द्वारा दिया गया है^*एफ)_x = एफ_f(x). इसके बाद यह निष्कर्ष निकलता है कि E से F तक f को कवर करने वाला बंडल मैप E से f तक बंडल मैप के समान है^*एम के ऊपर एफ।

विकल्प और सामान्यीकरण

बंडल मानचित्र की सामान्य अवधारणा में दो प्रकार की भिन्नताएँ हैं।

सबसे पहले, कोई विभिन्न श्रेणी के स्थानों में फाइबर बंडलों पर विचार कर सकता है। यह, उदाहरण के लिए, एक चिकने मैनिफोल्ड पर चिकने फाइबर बंडलों के बीच एक चिकने बंडल मानचित्र की धारणा की ओर ले जाता है।

दूसरा, कोई अपने फाइबर में अतिरिक्त संरचना वाले फाइबर बंडलों पर विचार कर सकता है, और इस संरचना को संरक्षित करने वाले बंडल मानचित्रों पर ध्यान केंद्रित कर सकता है। यह, उदाहरण के लिए, वेक्टर बंडलों के बीच एक (वेक्टर) बंडल होमोमोर्फिज्म की धारणा की ओर ले जाता है, जिसमें फाइबर वेक्टर रिक्त स्थान होते हैं, और एक बंडल मैप φ को प्रत्येक फाइबर पर एक रैखिक मानचित्र होना आवश्यक है। इस मामले में, ऐसे बंडल मैप φ (एफ को कवर करते हुए) को वेक्टर बंडल होम(ई,एफ के एक अनुभाग (फाइबर बंडल) के रूप में भी देखा जा सकता है^*F) या M, जिसका x से अधिक का फाइबर वेक्टर स्पेस होम है_x,एफ_f(x)) (एल(ई) को भी दर्शाया गया है_x,एफ_f(x))) से रेखीय मानचित्रों की इ_xएफ को_f(x).

श्रेणी:फाइबर बंडल श्रेणी:निरंतर कार्यों का सिद्धांत