फजी नियंत्रण प्रणाली

फ़ज़ी कंट्रोल" और "फ़ज़ी कंट्रोल" यहां पुनर्निर्देशित हैं। रॉक बैंड के लिए, फ़ज़ी कंट्रोल (बैंड) देखें।

फ़ज़ी नियंत्रण प्रणाली फजी तर्क पर आधारित एक नियंत्रण प्रणाली होता हैजिसे फजी तर्क पर आधारित किया जाता है - एक गणित प्रणाली जो गणितीय तार्किक चर के संदर्भ में एनालॉग संकेत इनपुट मानों का विश्लेषण करता है जो पारंपरिक या डिजिटल डाटा तर्क के विपरीत 0 और 1 के बीच निरंतर मान लेते हैं, जो केवल 1 या 0 के असतत मानों पर कार्य करता है।

एक फजी कंट्रोल सिस्टम एक कंट्रोल सिस्टम होता है जिसे फजी तर्क पर आधारित किया जाता है—एक गणितीय सिस्टम जो एनालॉग इनपुट मूल्यों का विश्लेषण करता है जिसे तार्किक मानों के रूप में विचार करता है जो 0 और 1 के बीच निरंतर मान लेते हैं, इसके खिलाफ क्लैसिकल या डिजिटल तर्क, जो केवल 1 या 0 (सत्य या असत्य, क्रमश:।) के डिस्क्रीट मानों पर कार्य करता है।

सिंहावलोकन

मशीन नियंत्रण में फ़ज़ी तर्क का व्यापक रूप से उपयोग किया जाता है। फ़ज़ी शब्द इस तथ्य को संदर्भित करता है कि इसमें शामिल तर्क उन अवधारणाओं से निपट सकता है जिन्हें सत्य या ग़लत के रूप में व्यक्त नहीं किया जा सकता है बल्कि आंशिक रूप से सत्य के रूप में व्यक्त किया जा सकता है। यद्यपि आनुवंशिक एल्गोरिदम और तंत्रिका नेटवर्क जैसे वैकल्पिक दृष्टिकोण कई मामलों में फ़ज़ी तर्क के समान ही कार्य कर सकते हैं, फ़ज़ी तर्क का लाभ यह है कि समस्या का समाधान उन शब्दों में दिया जा सकता है जिन्हें मानव ऑपरेटर समझ सकते हैं, ताकि उनका अनुभव बेहतर हो सके। नियंत्रक के डिजाइन में उपयोग किया जाता है। इससे उन कार्यों को यंत्रीकृत करना आसान हो जाता है जो पहले से ही मनुष्यों द्वारा सफलतापूर्वक किए जाते हैं।

इतिहास और अनुप्रयोग

फ़ज़ी तर्क को 1965 के एक पेपर में बर्कले में कैलिफोर्निया विश्वविद्यालय के लोटफ़ी ए. ज़ादेह द्वारा प्रस्तावित किया गया था। उन्होंने 1973 के एक पेपर में अपने विचारों को विस्तार से बताया, जिसमें भाषाई चर की अवधारणा पेश की गई, जो इस लेख में एक अस्पष्ट सेट के रूप में परिभाषित चर के बराबर है। पहले औद्योगिक अनुप्रयोग के साथ अन्य शोध भी हुए, डेनमार्क में एक सीमेंट भट्ठा बनाया गया, जो 1975 में लाइन पर आया।

फ़ज़ी सिस्टम प्रारंभ में जापान में लागू किए गए थे।

• फ़ज़ी सिस्टम में रुचि Hitachi के सेइजी यासुनोबू और सोजी मियामोतो द्वारा जगाई गई, जिन्होंने 1985 में ऐसे सिमुलेशन प्रदान किए जिन्होंने सेंदाई सबवे के लिए फ़ज़ी नियंत्रण सिस्टम की व्यवहार्यता का प्रदर्शन किया। उनके विचारों को अपनाया गया और 1987 में सेंदाई सबवे नंबोकू लाइन खुलने पर गति बढ़ाने, ब्रेक लगाने और रुकने को नियंत्रित करने के लिए फ़ज़ी सिस्टम का उपयोग किया गया।
• 1987 में, ताकेशी यामाकावा ने एक उलटा पेंडुलम प्रयोग में, सरल समर्पित फ़ज़ी तर्क चिप्स के एक सेट के माध्यम से, फ़ज़ी नियंत्रण के उपयोग का प्रदर्शन किया। यह एक क्लासिक नियंत्रण समस्या है, जिसमें एक वाहन आगे-पीछे चलते हुए अपने शीर्ष पर लगे खंभे को टिका लगाकर सीधा रखने की कोशिश करता है। यामाकावा ने बाद में पेंडुलम के शीर्ष पर पानी से भरे वाइन ग्लास और यहां तक ​​कि एक जीवित चूहे को रखकर प्रदर्शन को और अधिक परिष्कृत बना दिया: सिस्टम ने दोनों मामलों में स्थिरता बनाए रखी। यामाकावा ने अंततः क्षेत्र में अपने पेटेंट का फायदा उठाने में मदद करने के लिए अपनी स्वयं की फ़ज़ी-सिस्टम अनुसंधान प्रयोगशाला का आयोजन किया।
• जापानी इंजीनियरों ने बाद में औद्योगिक और उपभोक्ता दोनों अनुप्रयोगों के लिए फ़ज़ी सिस्टम की एक विस्तृत श्रृंखला विकसित की। 1988 में जापान ने इंटरनेशनल फ़ज़ी इंजीनियरिंग (LIFE) के लिए प्रयोगशाला की स्थापना की, जो फ़ज़ी अनुसंधान को आगे बढ़ाने के लिए 48 कंपनियों के बीच एक सहकारी व्यवस्था थी। ऑटोमोटिव कंपनी वोक्सवैगन LIFE की एकमात्र विदेशी कॉर्पोरेट सदस्य थी, जिसने तीन साल की अवधि के लिए एक शोधकर्ता को भेजा था।
• जापानी उपभोक्ता वस्तुओं में अक्सर फ़ज़ी सिस्टम शामिल होते हैं। मत्सुशिता वैक्यूम क्लीनर धूल सेंसर से पूछताछ करने और तदनुसार चूषण शक्ति को समायोजित करने के लिए फ़ज़ी एल्गोरिदम चलाने वाले माइक्रोकंट्रोलर का उपयोग करते हैं। हिताची वॉशिंग मशीनें लोड-वेट, फैब्रिक-मिक्स और डर्ट सेंसर के लिए फ़ज़ी कंट्रोलर का उपयोग करती हैं और बिजली, पानी और डिटर्जेंट के सर्वोत्तम उपयोग के लिए स्वचालित रूप से वॉश चक्र सेट करती हैं।
• कैनन ने एक ऑटोफोकसिंग कैमरा विकसित किया है जो अपने दृश्य क्षेत्र के छह क्षेत्रों में छवि की स्पष्टता को मापने के लिए चार्ज-युग्मित डिवाइस (सीसीडी) का उपयोग करता है और यह निर्धारित करने के लिए प्रदान की गई जानकारी का उपयोग करता है कि छवि फोकस में है या नहीं। यह फोकस करने के दौरान लेंस की गति में बदलाव की दर को भी ट्रैक करता है, और ओवरशूट को रोकने के लिए इसकी गति को नियंत्रित करता है। कैमरे का फ़ज़ी नियंत्रण प्रणाली 12 इनपुट का उपयोग करता है: 6 सीसीडी द्वारा प्रदान किए गए वर्तमान स्पष्टता डेटा को प्राप्त करने के लिए और 6 लेंस की गति में परिवर्तन की दर को मापने के लिए। आउटपुट लेंस की स्थिति है. फ़ज़ी नियंत्रण प्रणाली 13 नियमों का उपयोग करती है और इसके लिए 1.1 किलोबाइट मेमोरी की आवश्यकता होती है।
• मित्सुबिशी द्वारा डिज़ाइन किया गया एक औद्योगिक एयर कंडीशनर 25 हीटिंग नियमों और 25 कूलिंग नियमों का उपयोग करता है। एक तापमान सेंसर इनपुट प्रदान करता है, जिसमें नियंत्रण आउटपुट एक चर आवृत्ति ड्राइव, एक कंप्रेसर वाल्व और एक प्रशंसक मोटर को खिलाया जाता है। पिछले डिज़ाइन की तुलना में, फ़ज़ी नियंत्रक पांच गुना तेजी से गर्म और ठंडा होता है, बिजली की खपत 24% कम करता है, तापमान स्थिरता को दो गुना बढ़ा देता है, और कम सेंसर का उपयोग करता है।
• जांच किए गए या कार्यान्वित किए गए अन्य अनुप्रयोगों में शामिल हैं: चरित्र और लिखावट पहचान; ऑप्टिकल फ़ज़ी सिस्टम; रोबोट, जिनमें जापानी फूलों की सजावट करने वाला रोबोट भी शामिल है; आवाज नियंत्रण|आवाज-नियंत्रित रोबोट हेलीकॉप्टर (होवरिंग उल्टे पेंडुलम समस्या के समान एक संतुलन कार्य है); रोगी-विशिष्ट समाधान प्रदान करने के लिए पुनर्वास रोबोटिक्स (उदाहरण के लिए हृदय गति और रक्तचाप को नियंत्रित करने के लिए)। ); फिल्म निर्माण में पाउडर के प्रवाह का नियंत्रण; लिफ्ट प्रणाली; और इसी तरह।

फ़ज़ी सिस्टम पर काम उत्तरी अमेरिका और यूरोप में भी चल रहा है, हालाँकि जापान की तुलना में कम व्यापक पैमाने पर।

• अमेरिकी पर्यावरण संरक्षण एजेंसी ने कुशल ऊर्जा उपयोग|ऊर्जा-कुशल मोटरों के लिए फ़ज़ी नियंत्रण की जांच की है, और नासा ने स्वचालित अंतरिक्ष डॉकिंग के लिए फ़ज़ी नियंत्रण का अध्ययन किया है: सिमुलेशन से पता चलता है कि फ़ज़ी नियंत्रण प्रणाली ईंधन की खपत को काफी कम कर सकती है।
• बोइंग, जनरल मोटर्स, एलन-ब्राडली, क्रिसलर, ईटन कॉर्पोरेशन और व्हर्लपूल कॉर्पोरेशन जैसी कंपनियों ने कम-शक्ति वाले रेफ्रिजरेटर, बेहतर ऑटोमोटिव ट्रांसमिशन और ऊर्जा-कुशल इलेक्ट्रिक मोटर्स में उपयोग के लिए फ़ज़ी तर्क पर काम किया है।
• 1995 में मेटैग ने फ़ज़ी कंट्रोलर और वन-स्टॉप सेंसिंग मॉड्यूल पर आधारित एक बुद्धिमान डिशवॉशर पेश किया जो तापमान माप के लिए thermistor को जोड़ता है; धुलाई में मौजूद आयनों से डिटर्जेंट स्तर को मापने के लिए एक चालकता सेंसर; एक मैलापन सेंसर जो धुलाई की गंदगी को मापने के लिए बिखरे हुए और प्रसारित प्रकाश को मापता है; और स्पिन दर को पढ़ने के लिए एक मैग्नेटोस्ट्रिक्टिव सेंसर। सिस्टम कम से कम ऊर्जा, डिटर्जेंट और पानी के साथ सर्वोत्तम परिणाम प्राप्त करने के लिए किसी भी भार के लिए इष्टतम वॉश चक्र निर्धारित करता है। यहां तक ​​कि यह पिछली बार दरवाज़ा खोले जाने पर नज़र रखकर सूखे हुए खाद्य पदार्थों को भी समायोजित करता है, और दरवाज़ा खोले जाने की संख्या के आधार पर व्यंजनों की संख्या का अनुमान लगाता है।
• 2017 में Xiera Technologies Inc. ने फ़ज़ी तर्क कंट्रोलर के ज्ञान आधार के लिए पहला ऑटो-ट्यूनर विकसित किया, जिसे edeX के नाम से जाना जाता है। इस तकनीक का परीक्षण मोहॉक कॉलेज द्वारा किया गया था और यह गैर-रेखीय 2x2 और 3x3 मल्टी-इनपुट मल्टी-आउटपुट समस्याओं को हल करने में सक्षम थी।

फर्मवेयर, डिज़ाइन के विपरीत सॉफ़्टवेयर में फ़ज़ी अनुप्रयोगों पर अनुसंधान और विकास भी जारी है, जिसमें फ़ज़ी विशेषज्ञ सिस्टम और कृत्रिम तंत्रिका नेटवर्क के साथ फ़ज़ी तर्क का एकीकरण शामिल है|न्यूरल-नेटवर्क और तथाकथित अनुकूली आनुवंशिक एल्गोरिदम सॉफ़्टवेयर सिस्टम, अंतिम लक्ष्य के साथ स्व-शिक्षण फ़ज़ी-नियंत्रण प्रणाली का निर्माण। इन प्रणालियों को जटिल, अरेखीय गतिशील पौधों को नियंत्रित करने के लिए नियोजित किया जा सकता है, उदाहरण के लिए, मानव शरीर.

फजी सेट

See also: fuzzy set

फ़ज़ी नियंत्रण प्रणाली में इनपुट वैरिएबल सामान्यतः इसके समान सदस्यता फ़ंक्शन के सेट द्वारा मैप किए जाते हैं, जिन्हें फ़ज़ी सेट के रूप में जाना जाता है। क्रिस्प इनपुट वैल्यू को फ़ज़ी वैल्यू में बदलने की प्रक्रिया को फ़ज़िफिकेशन कहा जाता है। फ़ज़ी तर्क आधारित दृष्टिकोण पर दो फ़ज़ी सिस्टम डिज़ाइन करके विचार किया गया था, एक त्रुटि शीर्ष कोण के लिए और दूसरा वेग नियंत्रण के लिए। एक नियंत्रण प्रणाली में इसके एनालॉग इनपुट के साथ विभिन्न प्रकार के बदलना , या ऑन-ऑफ, इनपुट भी हो सकते हैं, और ऐसे स्विच इनपुट का सत्य मान हमेशा 1 या 0 के बराबर होगा, लेकिन योजना उनसे निपट सकती है सरलीकृत फ़ज़ी फ़ंक्शंस जो या तो एक मान या दूसरे होते हैं।

सदस्यता कार्यों और सत्य मूल्यों में इनपुट चर के मानचित्र (गणित) को देखते हुए, microcontroller नियमों के एक सेट के आधार पर निर्णय लेता है कि क्या कार्रवाई करनी है, प्रत्येक फॉर्म:

  यदि ब्रेक का तापमान गर्म है और गति बहुत तेज़ नहीं है
  फिर ब्रेक का दबाव थोड़ा कम हो जाता है।

इस उदाहरण में, दो इनपुट चर ब्रेक तापमान और गति हैं जिनके मान फ़ज़ी सेट के रूप में परिभाषित हैं। आउटपुट वेरिएबल, ब्रेक प्रेशर को एक फ़ज़ी सेट द्वारा भी परिभाषित किया जाता है जिसमें स्थिर या थोड़ा बढ़ा हुआ या थोड़ा कम आदि जैसे मान हो सकते हैं।

फ़ज़ी नियंत्रण विस्तार से

फ़ज़ी नियंत्रक अवधारणात्मक रूप से बहुत सरल हैं। इनमें एक इनपुट चरण, एक प्रोसेसिंग चरण और एक आउटपुट चरण शामिल होता है। इनपुट चरण सेंसर या अन्य इनपुट, जैसे स्विच, थंबव्हील इत्यादि को उचित सदस्यता कार्यों और सत्य मूल्यों पर मैप करता है। प्रसंस्करण चरण प्रत्येक उपयुक्त नियम को लागू करता है और प्रत्येक के लिए एक परिणाम उत्पन्न करता है, फिर नियमों के परिणामों को जोड़ता है। अंत में, आउटपुट चरण संयुक्त परिणाम को वापस एक विशिष्ट नियंत्रण आउटपुट मान में परिवर्तित करता है।

सदस्यता कार्यों का सबसे आम आकार त्रिकोणीय है, हालांकि ट्रैपेज़ॉइडल और बेल वक्र का भी उपयोग किया जाता है, लेकिन आकार आम तौर पर वक्रों की संख्या और उनके स्थान से कम महत्वपूर्ण होता है। इनपुट मान की आवश्यक सीमा, या अस्पष्ट शब्दजाल में प्रवचन के ब्रह्मांड को कवर करने के लिए तीन से सात वक्र आम तौर पर उपयुक्त होते हैं।

जैसा कि पहले चर्चा की गई है, प्रसंस्करण चरण IF-THEN कथनों के रूप में तर्क नियमों के संग्रह पर आधारित है, जहां IF भाग को पूर्ववर्ती कहा जाता है और THEN भाग को परिणामी कहा जाता है। विशिष्ट फ़ज़ी नियंत्रण प्रणालियों में दर्जनों नियम होते हैं।

थर्मोस्टेट के लिए एक नियम पर विचार करें:

  यदि (तापमान ठंडा है) तो पलटें (हीटर अधिक है)

यह नियम हीटर आउटपुट के लिए फ़ज़ी सेट में परिणाम उत्पन्न करने के लिए तापमान इनपुट के सत्य मान का उपयोग करता है, जो ठंड का कुछ सत्य मान है, जो उच्च का कुछ मान है। अंत में क्रिस्प कंपोजिट आउटपुट उत्पन्न करने के लिए इस परिणाम का उपयोग अन्य नियमों के परिणामों के साथ किया जाता है। जाहिर है, ठंड का सत्य मूल्य जितना अधिक होगा, उच्च का सत्य मूल्य उतना ही अधिक होगा, हालांकि इसका मतलब यह नहीं है कि आउटपुट स्वयं उच्च पर सेट हो जाएगा क्योंकि यह कई नियमों में से केवल एक नियम है। कुछ मामलों में, सदस्यता कार्यों को हेजेज द्वारा संशोधित किया जा सकता है जो क्रियाविशेषण के समतुल्य हैं। सामान्य हेजेज में लगभग, निकट, करीब, लगभग, बहुत, थोड़ा, बहुत, अत्यधिक और कुछ हद तक शामिल हैं। इन परिचालनों की सटीक परिभाषाएँ हो सकती हैं, हालाँकि विभिन्न कार्यान्वयनों के बीच परिभाषाएँ काफी भिन्न हो सकती हैं। बहुत, एक उदाहरण के लिए, वर्ग सदस्यता कार्य; चूँकि सदस्यता मान हमेशा 1 से कम होता है, इससे सदस्यता कार्य सीमित हो जाता है। अधिक संकीर्णता देने के लिए मानों को अत्यधिक घन करता है, जबकि वर्गमूल लेकर फ़ंक्शन को कुछ हद तक विस्तृत करता है।

व्यवहार में, फ़ज़ी नियम सेट में आमतौर पर कई पूर्ववृत्त होते हैं जिन्हें फ़ज़ी ऑपरेटरों का उपयोग करके संयोजित किया जाता है, जैसे कि AND, OR, और NOT, हालाँकि फिर से परिभाषाएँ भिन्न होती हैं: AND, एक लोकप्रिय परिभाषा में, बस सभी के न्यूनतम वजन का उपयोग करता है पूर्ववृत्त, जबकि OR अधिकतम मान का उपयोग करता है। एक NOT ऑपरेटर भी है जो पूरक फ़ंक्शन देने के लिए सदस्यता फ़ंक्शन को 1 से घटाता है।

किसी नियम के परिणाम को परिभाषित करने के कई तरीके हैं, लेकिन सबसे आम और सरल में से एक अधिकतम-न्यूनतम अनुमान विधि है, जिसमें आउटपुट सदस्यता फ़ंक्शन को आधार द्वारा उत्पन्न सत्य मान दिया जाता है।

नियमों को हार्डवेयर में समानांतर रूप से, या सॉफ़्टवेयर में क्रमिक रूप से हल किया जा सकता है। लागू किए गए सभी नियमों के परिणामों को कई तरीकों में से एक द्वारा स्पष्ट मूल्य पर डिफ्यूज़ किया जाता है। सिद्धांत रूप में, ऐसे दर्जनों हैं, जिनमें से प्रत्येक के विभिन्न फायदे या नुकसान हैं।

सेंट्रोइड विधि बहुत लोकप्रिय है, जिसमें परिणाम के द्रव्यमान का केंद्र स्पष्ट मूल्य प्रदान करता है। दूसरा दृष्टिकोण ऊंचाई विधि है, जो सबसे बड़े योगदानकर्ता का मान लेता है। केन्द्रक विधि सबसे बड़े क्षेत्र के आउटपुट वाले नियम का पक्ष लेती है, जबकि ऊँचाई विधि स्पष्ट रूप से सबसे बड़े आउटपुट मान वाले नियम का पक्ष लेती है।

नीचे दिया गया चित्र इनपुट वेरिएबल x, y, और z और एक आउटपुट वेरिएबल n वाले सिस्टम के लिए अधिकतम-न्यूनतम अनुमान और सेंट्रोइड डिफ्यूज़िफिकेशन को दर्शाता है। ध्यान दें कि म्यू सत्य मान के लिए मानक फ़ज़ी-तर्क नामकरण है:

ध्यान दें कि प्रत्येक नियम आउटपुट वैरिएबल के लिए किसी विशेष सदस्यता फ़ंक्शन के सत्य मान के रूप में परिणाम कैसे प्रदान करता है। सेंट्रोइड डिफ्यूज़िफिकेशन में मानों को OR'd किया जाता है, अर्थात, अधिकतम मान का उपयोग किया जाता है और मान नहीं जोड़े जाते हैं, और फिर परिणामों को सेंट्रोइड गणना का उपयोग करके संयोजित किया जाता है।

फ़ज़ी नियंत्रण प्रणाली का डिज़ाइन अनुभवजन्य तरीकों पर आधारित है, जो मूल रूप से परीक्षण-और-त्रुटि के लिए एक व्यवस्थित दृष्टिकोण है। सामान्य प्रक्रिया इस प्रकार है:

• सिस्टम के परिचालन विनिर्देशों और इनपुट और आउटपुट का दस्तावेजीकरण करें।
• इनपुट के लिए फ़ज़ी सेट का दस्तावेज़ीकरण करें।
• नियम सेट का दस्तावेजीकरण करें।
• डिफ्यूज़िफिकेशन विधि निर्धारित करें।
• सिस्टम को सत्यापित करने के लिए परीक्षण सूट चलाएं, आवश्यकतानुसार विवरण समायोजित करें।
• दस्तावेज़ पूरा करें और उत्पादन के लिए जारी करें।

एक सामान्य उदाहरण के रूप में, भाप टरबाइन के लिए फ़ज़ी नियंत्रक के डिज़ाइन पर विचार करें। इस नियंत्रण प्रणाली का ब्लॉक आरेख इस प्रकार दिखता है:

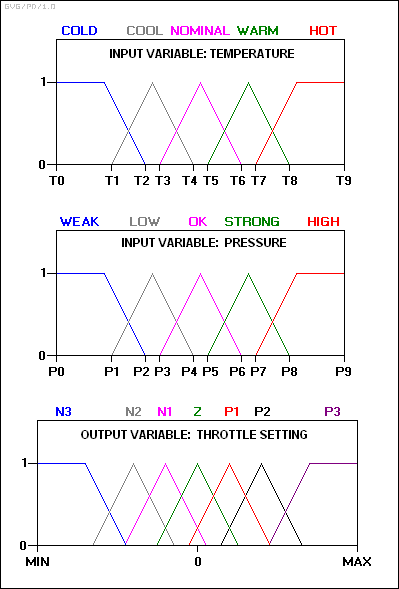
इनपुट और आउटपुट वैरिएबल निम्नलिखित फ़ज़ी सेट में मैप होते हैं:

-कहाँ:

  N3: बड़ा नकारात्मक.
  एन2: मध्यम नकारात्मक।
  एन1: छोटा नकारात्मक.
  जेड: शून्य.
  P1: छोटा सकारात्मक.
  पी2: मध्यम सकारात्मक।
  पी3: बड़ा सकारात्मक.

नियम सेट में ऐसे नियम शामिल हैं:

नियम 1: यदि तापमान ठंडा है और दबाव कमजोर है,
         तब थ्रॉटल P3 है।

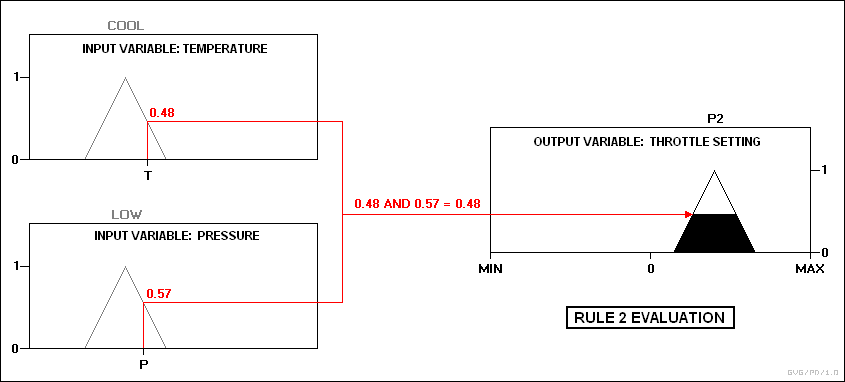
नियम 2: यदि तापमान ठंडा है और दबाव कम है,
         तब थ्रॉटल P2 है।

नियम 3: यदि तापमान ठंडा है और दबाव ठीक है,
         तब थ्रॉटल Z है.

नियम 4: यदि तापमान ठंडा है और दबाव मजबूत है,
         तब थ्रोटल N2 है।

व्यवहार में, नियंत्रक इनपुट स्वीकार करता है और उन्हें अपने सदस्यता कार्यों और सत्य मूल्यों में मैप करता है। फिर इन मैपिंग को नियमों में शामिल किया जाता है। यदि नियम दो इनपुट चर के मैपिंग के बीच एक AND संबंध निर्दिष्ट करता है, जैसा कि ऊपर दिए गए उदाहरणों में है, तो दोनों में से न्यूनतम का उपयोग संयुक्त सत्य मान के रूप में किया जाता है; यदि कोई OR निर्दिष्ट है, तो अधिकतम का उपयोग किया जाता है। उपयुक्त आउटपुट स्थिति का चयन किया जाता है और परिसर के सत्य स्तर पर सदस्यता मूल्य निर्दिष्ट किया जाता है। तब सत्य मूल्य धूमिल हो जाते हैं। उदाहरण के लिए, मान लें कि तापमान ठंडी अवस्था में है, और दबाव निम्न और ठीक अवस्था में है। दबाव मान यह सुनिश्चित करते हैं कि केवल नियम 2 और 3 ही फायर करें:

फिर दो आउटपुट को सेंट्रोइड डिफ्यूज़िफिकेशन के माध्यम से डिफ़ज़िफ़ाई किया जाता है: <पूर्व>

  ________________________________________________________________________

                                      | ज़ेड पी2
                                   1 -+* *
                                      | * * * *
                                      | * * * *
                                      | * * * *
                                      | *2222222222
                                      | *222222222222
                                      | 33333333222222222222
                                      +---333333332222222222222222-->
                                                       ^
                                                     +150
  ________________________________________________________________________

</पूर्व>

आउटपुट मान थ्रॉटल को समायोजित करेगा और फिर अगला मान उत्पन्न करने के लिए नियंत्रण चक्र फिर से शुरू होगा।

एक फजी नियंत्रक का निर्माण

माइक्रोकंट्रोलर चिप के साथ एक सरल फीडबैक नियंत्रक लागू करने पर विचार करें:

इनपुट त्रुटि चर ई के लिए एक फ़ज़ी सेट परिभाषित किया गया है, और त्रुटि, डेल्टा, साथ ही आउटपुट में व्युत्पन्न परिवर्तन निम्नानुसार है:

  एल.पी.: बड़ा सकारात्मक
  एसपी: छोटा सा सकारात्मक
  ज़ी: शून्य
  एसएन: छोटा नकारात्मक
  एलएन: बड़ा नकारात्मक

यदि त्रुटि -1 से +1 तक होती है, जिसमें उपयोग किए गए एनालॉग-टू-डिजिटल कनवर्टर का रिज़ॉल्यूशन 0.25 है, तो इनपुट वेरिएबल का फ़ज़ी सेट (जो, इस मामले में, आउटपुट वेरिएबल पर भी लागू होता है) को बहुत वर्णित किया जा सकता है बस एक तालिका के रूप में, शीर्ष पंक्ति में त्रुटि / डेल्टा / आउटपुट मान और नीचे की पंक्तियों में प्रत्येक सदस्यता फ़ंक्शन के लिए सत्य मान व्यवस्थित किए गए हैं:

  ____________________________________________________________________________

              -1 -0.75 -0.5 -0.25 0 0.25 0.5 0.75 1
  ____________________________________________________________________________

   म्यू(एलपी) 0 0 0 0 0 0 0.3 0.7 1
   म्यू(एसपी) 0 0 0 0 0.3 0.7 1 0.7 0.3
   म्यू(ZE) 0 0 0.3 0.7 1 0.7 0.3 0 0
   म्यू(एसएन) 0.3 0.7 1 0.7 0.3 0 0 0 0
   म्यू(एलएन) 1 0.7 0.3 0 0 0 0 0 0
  ______________________________________________________________________________________ -या, ग्राफ़िकल रूप में (जहां प्रत्येक X का मान 0.1 है):

         एलएन एसएन जेडई एसपी एलपी
      +---------------------------------------------------------------- -----------------+
      | |
-1.0 | XXXXXXXXXX XXX : : : |
-0.75 | XXXXXXX XXXXXXX : : : |
-0.5 | XXX XXXXXXXXXX XXX : : |
-0.25 | : XXXXXXX XXXXXXX : : |
 0.0 | : XXX XXXXXXXXXX XXX : |
 0.25 | : : XXXXXXX XXXXXXX : |
 0.5 | : : XXX XXXXXXXXXX XXX |
 0.75 | : : : XXXXXXX XXXXXXX |
 1.0 | : : : XXX XXXXXXXXX |
      | |
      +---------------------------------------------------------------- -----------------+

मान लीजिए कि इस फ़ज़ी सिस्टम का निम्नलिखित नियम आधार है:

  नियम 1: यदि e = ZE और डेल्टा = ZE तो आउटपुट = ZE
  नियम 2: यदि ई = जेडई और डेल्टा = एसपी तो आउटपुट = एसएन
  नियम 3: यदि ई = एसएन और डेल्टा = एसएन तो आउटपुट = एलपी
  नियम 4: यदि ई = एलपी या डेल्टा = एलपी तो आउटपुट = एलएन

ये नियम नियंत्रण अनुप्रयोगों के लिए विशिष्ट हैं क्योंकि पूर्ववर्ती में त्रुटि और त्रुटि-डेल्टा संकेतों का तार्किक संयोजन होता है, जबकि परिणामी एक नियंत्रण कमांड आउटपुट होता है। नियम आउटपुट को असतत सेंट्रोइड गणना का उपयोग करके डिफ्यूज़ किया जा सकता है:

  SUM( I = 1 से 4 OF ( mu(I) * आउटपुट(I) ) ) / SUM( I = 1 से 4 OF mu(I) )

अब, मान लीजिए कि किसी निश्चित समय पर:

  ई = 0.25
  डेल्टा = 0.5

तब यह देता है:

  ________________________

              ई डेल्टा
  ________________________

  म्यू(एलपी) 0 0.3
  म्यू(एसपी) 0.7 1
  म्यू(ZE) 0.7 0.3
  म्यू(एसएन) 0 0
  म्यू(एलएन) 0 0
  ________________________

इसे नियम 1 में प्लग करने पर यह मिलता है:

  नियम 1: यदि e = ZE और डेल्टा = ZE तो आउटपुट = ZE
 
     म्यू(1) = न्यूनतम(0.7, 0.3) = 0.3
     आउटपुट(1) = 0

-- कहाँ:

• म्यू(1): नियम 1 के लिए परिणाम सदस्यता फ़ंक्शन का सत्य मान। एक केन्द्रक गणना के संदर्भ में, यह इस असतत मामले के लिए इस परिणाम का द्रव्यमान है।
• आउटपुट(1): मान (नियम 1 के लिए) जहां परिणाम सदस्यता फ़ंक्शन (जेडई) आउटपुट वेरिएबल फ़ज़ी सेट रेंज पर अधिकतम है। अर्थात्, केन्द्रक गणना के संदर्भ में, मास के केंद्र का स्थानइस व्यक्तिगत परिणाम के लिए। यह मान म्यू के मान से स्वतंत्र है। यह बस आउटपुट रेंज के साथ ZE के स्थान की पहचान करता है।

अन्य नियम देते हैं:

  नियम 2: यदि ई = जेडई और डेल्टा = एसपी तो आउटपुट = एसएन

     म्यू(2) = मिन(0.7, 1 ) = 0.7
     आउटपुट(2) = -0.5

  नियम 3: यदि ई = एसएन और डेल्टा = एसएन तो आउटपुट = एलपी

     म्यू(3) = न्यूनतम(0.0, 0.0) = 0
     आउटपुट(3) = 1

  नियम 4: यदि ई = एलपी या डेल्टा = एलपी तो आउटपुट = एलएन

     म्यू(4) = मैक्स( 0.0, 0.3 ) = 0.3
     आउटपुट(4) = -1

केन्द्रक गणना से प्राप्त होता है:

${\frac {mu(1)\cdot output(1)+mu(2)\cdot output(2)+mu(3)\cdot output(3)+mu(4)\cdot output(4)}{mu(1)+mu(2)+mu(3)+mu(4)}}$

  $={\frac {(0.3\cdot 0)+(0.7\cdot -0.5)+(0\cdot 1)+(0.3\cdot -1)}{0.3+0.7+0+0.3}}$
  $=-0.5$-अंतिम नियंत्रण आउटपुट के लिए। सरल। बेशक कठिन हिस्सा यह पता लगाना है कि वास्तव में कौन से नियम व्यवहार में सही ढंग से काम करते हैं।

यदि आपको सेंट्रोइड समीकरण का पता लगाने में समस्या हो रही है, तो याद रखें कि सेंट्रॉइड को गुरुत्वाकर्षण के केंद्र के चारों ओर सभी क्षणों (स्थान समय द्रव्यमान) को जोड़कर और योग को शून्य के बराबर करके परिभाषित किया जाता है। तो यदि $X_{0}$ गुरुत्वाकर्षण का केंद्र है, $X_{i}$ प्रत्येक द्रव्यमान का स्थान है, और $M_{i}$ प्रत्येक द्रव्यमान है, यह देता है:

$0=(X_{1}-X_{0})\cdot M_{1}+(X_{2}-X_{0})\cdot M_{2}+\ldots +(X_{n}-X_{0})\cdot M_{n}$

  $0=(X_{1}\cdot M_{1}+X_{2}\cdot M_{2}+\ldots +X_{n}\cdot M_{n})-X_{0}\cdot (M_{1}+M_{2}+\ldots +M_{n})$
  $X_{0}\cdot (M_{1}+M_{2}+\ldots +M_{n})=X_{1}\cdot M_{1}+X_{2}\cdot M_{2}+\ldots +X_{n}\cdot M_{n}$
  $X_{0}={\frac {X_{1}\cdot M_{1}+X_{2}\cdot M_{2}+\ldots +X_{n}\cdot M_{n}}{M_{1}+M_{2}+\ldots +M_{n}}}$

हमारे उदाहरण में, म्यू का मान द्रव्यमान के अनुरूप है, और एक्स का मान द्रव्यमान के स्थान के अनुरूप है (म्यू, हालांकि, केवल 'द्रव्यमान से मेल खाता है' यदि आउटपुट फ़ंक्शन का प्रारंभिक 'द्रव्यमान' सभी समान/समतुल्य है। यदि वे समान नहीं हैं, यानी कुछ संकीर्ण त्रिकोण हैं, जबकि अन्य शायद चौड़े ट्रेपेज़ॉइड या कंधे वाले त्रिकोण हैं , तो आउटपुट फ़ंक्शन का द्रव्यमान या क्षेत्र ज्ञात होना चाहिए या गणना की जानी चाहिए। यह वह द्रव्यमान है जिसे म्यू द्वारा स्केल किया जाता है और इसके स्थान X_i से गुणा किया जाता है)।

इस प्रणाली को एक मानक माइक्रोप्रोसेसर पर लागू किया जा सकता है, लेकिन समर्पित फ़ज़ी चिप्स अब उपलब्ध हैं। उदाहरण के लिए, सैन जोस, कैलिफ़ोर्निया की एडेप्टिव तर्क INC, एक फ़ज़ी चिप, AL220 बेचती है, जो चार एनालॉग इनपुट स्वीकार कर सकती है और चार एनालॉग आउटपुट उत्पन्न कर सकती है। चिप का ब्लॉक आरेख नीचे दिखाया गया है:

<पूर्व>

             +------+ +------+
एनालॉग --4-->| एनालॉग | | mux / +--4-->एनालॉग
  में | मक्स | | एसएच | बाहर
             +----+----+ +-------+
                  | ^
                  वी |
           +----------------+ +--+--+
           | एडीसी/कुंडी | | डीएसी |
           +------+------+ +-----+
                  | ^
                  | |
                  8+--------------------------------+
                  | | |
                  | वी |
                  | +-------+ +----+ |
                  +-->| फजीफायर | | डिफ्यूज़ीफायर +--+
                      +-----+-----+ +-----+
                            | ^
                            | +----------------+ |
                            | | नियम | |
                            +->| प्रोसेसर +--+
                               | (50 नियम) |
                               +------+------+
                                      |
                               +------+------+
                               | पैरामीटर |
                               | स्मृति |
                               | 256 x 8 |
                               +----------------+

   एडीसी: एनालॉग-टू-डिजिटल कनवर्टर
   डीएसी: डिजिटल-टू-एनालॉग कनवर्टर
   एसएच: नमूना/पकड़

</पूर्व>

एंटीलॉक ब्रेक

उदाहरण के तौर पर, एक माइक्रोकंट्रोलर चिप द्वारा निर्देशित लॉक - रोधी ब्रेकिंग प्रणाली पर विचार करें। माइक्रोकंट्रोलर को ब्रेक तापमान, गति और सिस्टम में अन्य चर के आधार पर निर्णय लेना होता है।

इस प्रणाली में परिवर्तनशील तापमान को कई अवस्थाओं में विभाजित किया जा सकता है: ठंडा, ठंडा, मध्यम, गर्म, गर्म, बहुत गर्म। एक अवस्था से दूसरी अवस्था में संक्रमण को परिभाषित करना कठिन है।

गर्म को गर्म से विभाजित करने के लिए एक मनमाना स्थैतिक सीमा निर्धारित की जा सकती है। उदाहरण के लिए, ठीक 90 डिग्री पर, गर्म समाप्त होता है और गर्म शुरू होता है। लेकिन जब इनपुट मान उस सीमा से अधिक हो जाएगा तो इसके परिणामस्वरूप एक असंतत परिवर्तन होगा। संक्रमण सुचारू नहीं होगा, जैसा कि ब्रेकिंग स्थितियों में आवश्यक होगा।

इसका तरीका राज्यों को अस्पष्ट बनाना है। यानी उन्हें धीरे-धीरे एक अवस्था से दूसरी अवस्था में बदलने दें। ऐसा करने के लिए, विभिन्न कारकों के बीच एक गतिशील संबंध स्थापित होना चाहिए।

सदस्यता फ़ंक्शंस का उपयोग करके इनपुट तापमान स्थिति को परिभाषित करके प्रारंभ करें:

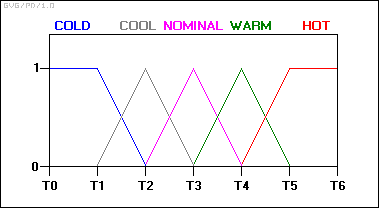इस योजना के साथ, इनपुट वैरिएबल की स्थिति अब अचानक एक राज्य से दूसरे राज्य में नहीं जाती है। इसके बजाय, जैसे-जैसे तापमान बदलता है, यह एक सदस्यता फ़ंक्शन में मूल्य खो देता है जबकि अगले में मूल्य प्राप्त करता है। दूसरे शब्दों में, जैसे-जैसे यह गर्म श्रेणी में उच्च स्थान पर होता जाता है, ठंड की श्रेणी में इसकी रैंकिंग कम होती जाती है।

किसी भी नमूना समय सीमा पर, ब्रेक तापमान का सत्य मान लगभग हमेशा दो सदस्यता कार्यों के कुछ डिग्री हिस्से में होगा: यानी: '0.6 नाममात्र और 0.4 गर्म', या '0.7 नाममात्र और 0.3 ठंडा', और इसी तरह।

उपरोक्त उदाहरण एकाधिक मानों से मानों के अमूर्तन का उपयोग करते हुए एक सरल अनुप्रयोग को प्रदर्शित करता है। हालाँकि, यह केवल एक प्रकार के डेटा का प्रतिनिधित्व करता है, इस मामले में, तापमान।

डिज़ाइन किए गए फ़ज़ी सिस्टम के अनुसार, इस ब्रेकिंग सिस्टम में अतिरिक्त परिष्कार जोड़ना, ट्रैक्शन (इंजीनियरिंग), गति, जड़ता, गतिशील कार्यों में स्थापित अतिरिक्त कारकों द्वारा किया जा सकता है।

फ़ज़ी नियंत्रण की तार्किक व्याख्या

उपस्थिति के बावजूद IF-THEN नियमों की कठोर तार्किक व्याख्या देने में कई कठिनाइयाँ हैं। उदाहरण के तौर पर, पहले क्रम सूत्र Cold(x)→High(y) द्वारा IF (तापमान ठंडा है) THEN (हीटर उच्च है) के रूप में एक नियम की व्याख्या करें और मान लें कि r एक इनपुट है जैसे कि Cold(r) गलत है। फिर सूत्र Cold(r)→High(t) किसी भी t के लिए सत्य है और इसलिए कोई भी t दिए गए r पर सही नियंत्रण देता है। फ़ज़ी नियंत्रण का एक कठोर तार्किक औचित्य हाजेक की पुस्तक में दिया गया है (अध्याय 7 देखें) जहाँ फ़ज़ी नियंत्रण को हाजेक के मूल तर्क के सिद्धांत के रूप में दर्शाया गया है।

गेर्ला 2005 में फ़ज़ी नियंत्रण के लिए एक और तार्किक दृष्टिकोण फ़ज़ी तर्क प्रोग्रामिंग के आधार पर प्रस्तावित है: नियमों की IF-THEN प्रणाली से उत्पन्न होने वाले फ़ज़ी फ़ंक्शन को f द्वारा निरूपित करें। फिर इस प्रणाली को एक फ़ज़ी प्रोग्राम P में अनुवादित किया जा सकता है जिसमें नियमों की एक श्रृंखला होती है जिसका शीर्ष Good(x,y) है। पी के कम से कम अस्पष्ट हेरब्रांड मॉडल में इस विधेय की व्याख्या एफ के साथ मेल खाती है। यह फ़ज़ी नियंत्रण के लिए और भी उपयोगी उपकरण देता है।

अस्पष्ट गुणात्मक अनुकरण

इससे पहले कि कोई आर्टिफिशियल इंटेलिजेंस सिस्टम कार्रवाई अनुक्रम की योजना बना सके, किसी प्रकार के गणितीय मॉडल की आवश्यकता होती है। वीडियो गेम के लिए, मॉडल गेम के नियमों के बराबर है। प्रोग्रामिंग परिप्रेक्ष्य से, खेल के नियमों को एक भौतिकी इंजन के रूप में लागू किया जाता है जो एक खिलाड़ी से एक कार्रवाई स्वीकार करता है और गणना करता है कि क्या कार्रवाई वैध है। कार्रवाई निष्पादित होने के बाद, गेम अनुवर्ती स्थिति में है। यदि उद्देश्य केवल गणितीय गेम खेलना नहीं है, बल्कि वास्तविक दुनिया के अनुप्रयोगों के लिए क्रियाओं का निर्धारण करना है, तो सबसे स्पष्ट बाधा यह है कि गेम के कोई नियम उपलब्ध नहीं हैं। पहला कदम डोमेन को मॉडल करना है। सिस्टम की पहचान सटीक गणितीय समीकरणों या फ़ज़ी नियमों के साथ की जा सकती है। किसी डोमेन के लिए आंतरिक मॉडल (मोटर नियंत्रण)#फॉरवर्ड मॉडल बनाने के लिए फ़ज़ी तर्क और अनुकूली न्यूरो फ़ज़ी अनुमान प्रणाली सिस्टम (एडेप्टिव नेटवर्क आधारित फ़ज़ी इंट्रेंस सिस्टम) का उपयोग करने के कई नुकसान हैं। गुणात्मक अनुकरण सही अनुवर्ती स्थिति निर्धारित करने में सक्षम नहीं है, लेकिन सिस्टम केवल अनुमान लगाएगा कि यदि कार्रवाई की गई तो क्या होगा। फ़ज़ी गुणात्मक सिमुलेशन सटीक संख्यात्मक मानों की भविष्यवाणी नहीं कर सकता है, लेकिन यह भविष्य के बारे में अनुमान लगाने के लिए सटीक प्राकृतिक भाषा का उपयोग कर रहा है। यह वर्तमान स्थिति और अतीत की कार्रवाइयों को लेता है और खेल की अपेक्षित अनुवर्ती स्थिति उत्पन्न करता है।

ANFIS सिस्टम का आउटपुट सही जानकारी नहीं दे रहा है, बल्कि केवल फजी सेट नोटेशन प्रदान कर रहा है, उदाहरण के लिए [0,0.2,0.4,0]। सेट नोटेशन को वापस संख्यात्मक मानों में परिवर्तित करने के बाद सटीकता खराब हो जाती है। यह फ़ज़ी गुणात्मक सिमुलेशन को व्यावहारिक अनुप्रयोगों के लिए एक ख़राब विकल्प बनाता है।

अनुप्रयोग

फ़ज़ी नियंत्रण प्रणालियाँ तब उपयुक्त होती हैं जब प्रक्रिया की जटिलता अनिश्चितता और अरेखीय व्यवहार सहित अधिक होती है, और कोई सटीक गणितीय मॉडल उपलब्ध नहीं होते हैं। 80 के दशक से अग्रणी समाधानों के साथ दुनिया भर में मुख्य रूप से जापान में फ़ज़ी नियंत्रण प्रणालियों के सफल अनुप्रयोगों की सूचना मिली है।

साहित्य में बताए गए कुछ अनुप्रयोग हैं:

• एयर कंडिशनर
• कैमरों में स्वचालित फोकस प्रणाली
• घरेलू उपकरण (रेफ्रिजरेटर, वॉशिंग मशीन...)
• औद्योगिक प्रक्रियाओं और प्रणाली का नियंत्रण और अनुकूलन
• लेखन प्रणाली
• इंजनों में ईंधन दक्षता
• पर्यावरण
• विशेषज्ञ प्रणालियां
• निर्णय के पेड़
• रोबोटिक्स
• स्वायत्त वाहन

यह भी देखें

• गतिशील तर्क (मोडल तर्क)
• बायेसियन अनुमान
• फ़ंक्शन सन्निकटन
• फजी अवधारणा
• अस्पष्ट मार्कअप भाषा
• हिस्टैरिसीस
• तंत्रिका - तंत्र
• न्यूरो फजी
• अस्पष्ट नियंत्रण भाषा
• टाइप-2 फ़ज़ी सेट और सिस्टम

अग्रिम पठन

• Kevin M. Passino and Stephen Yurkovich, Fuzzy Control, Addison Wesley Longman, Menlo Park, CA, 1998 (522 pages)
• Kazuo Tanaka; Hua O. Wang (2001). Fuzzy control systems design and analysis: a linear matrix inequality approach. John Wiley and Sons. ISBN 978-0-471-32324-2.
• Cox, E. (Oct. 1992). Fuzzy fundamentals. IEEE Spectrum, 29:10. pp. 58–61.
• Cox, E. (Feb. 1993) Adaptive fuzzy systems. IEEE Spectrum, 30:2. pp. 7–31.
• Jan Jantzen, "Tuning Of Fuzzy PID Controllers", Technical University of Denmark, report 98-H 871, September 30, 1998. [1]
• Jan Jantzen, Foundations of Fuzzy Control. Wiley, 2007 (209 pages) (Table of contents)
• Computational Intelligence: A Methodological Introduction by Kruse, Borgelt, Klawonn, Moewes, Steinbrecher, Held, 2013, Springer, ISBN 9781447150121

बाहरी संबंध

• Robert Babuska and Ebrahim Mamdani, ed. (2008). "Fuzzy control". Scholarpedia. Retrieved 31 December 2022.
• Introduction to Fuzzy Control
• Fuzzy Logic in Embedded Microcomputers and Control Systems
• IEC 1131-7 CD1 Archived 2021-03-04 at the Wayback Machine IEC 1131-7 CD1 PDF
• Online interactive demonstration of a system with 3 fuzzy rules
• Data driven fuzzy systems