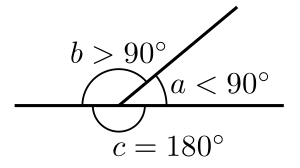कोण

Not to be confused with Angel.

This article is about angles in geometry. For other uses, see कोण (disambiguation).

एक शीर्ष से निकलने वाली दो किरणों द्वारा निर्मित कोण।

यूक्लिडियन ज्यामिति में, एक कोण दो किरणों द्वारा बनाई गई आकृति है, जिसे कोण के पक्ष कहा जाता है, जो एक सामान्य समापन बिंदु को साझा करता है, जिसे कोण का शीर्ष कहा जाता है।दो किरणों से बनने वाले कोण उस तल में होते हैं जिसमें किरणें होती हैं। कोण भी दो तलों के प्रतिच्छेदन से बनते हैं। इन्हें डायहेड्रल कोण कहा जाता है। दो प्रतिच्छेदी वक्र भी एक कोण को परिभाषित कर सकते हैं, जो कि उनके प्रतिच्छेदन बिंदु पर संबंधित वक्रों के स्पर्शरेखा वाली किरणों का कोण होता है।

कोण का उपयोग कोण या घूर्णन के माप को निर्दिष्ट करने के लिए भी किया जाता है। यह माप एक वृत्ताकार चाप की लंबाई और उसकी त्रिज्या का अनुपात है। एक ज्यामितीय कोण के मामले में, चाप शीर्ष पर केंद्रित होता है और पक्षों द्वारा सीमांकित होता है। घूर्णन के मामले में, चाप घूर्णन के केंद्र में केंद्रित होता है और किसी अन्य बिंदु से और घूर्णन द्वारा इसकी छवि को सीमित करता है।

इतिहास और व्युत्पत्ति

कोण शब्द लैटिन शब्द एंगुलस से आया है, जिसका अर्थ है कोना; सजातीय शब्द ग्रीक हैं ἀγκύλος (ankylοs), जिसका अर्थ है कुटिल, घुमावदार, और अंग्रेजी शब्द टखने। दोनों प्रोटो-इंडो-यूरोपीय भाषा से जुड़े हुए हैं | प्रोटो-इंडो-यूरोपियन रूट * एंक-, जिसका अर्थ है झुकना या झुकना।

यूक्लिड एक समतल कोण को एक दूसरे के झुकाव के रूप में परिभाषित करता है, एक समतल में, दो रेखाएँ जो एक दूसरे से मिलती हैं, और एक दूसरे के संबंध में सीधे झूठ नहीं बोलती हैं। प्रोक्लस के अनुसार, कोण या तो गुणवत्ता या मात्रा, या संबंध होना चाहिए। पहली अवधारणा का उपयोग यूडेमस द्वारा किया गया था, जो एक कोण को एक सीधी रेखा से विचलन के रूप में मानते थे; दूसरा अन्ताकिया के कार्पस द्वारा, जिसने इसे प्रतिच्छेदन रेखाओं के बीच का अंतराल या स्थान माना; यूक्लिड ने तीसरी अवधारणा को अपनाया।

कोणों की पहचान

गणितीय अभिव्यक्तियों में, ग्रीक अक्षरों का उपयोग करना आम है (α, β, γ, θ, φ, . . . ) किसी कोण के आकार को दर्शाने वाले चर के रूप में (इसके अन्य अर्थ के साथ भ्रम से बचने के लिए, प्रतीक π आमतौर पर इस उद्देश्य के लिए उपयोग नहीं किया जाता है)। लोअरकेस रोमन अक्षरों (ए, बी, सी, . . . ) का भी उपयोग किया जाता है। ऐसे संदर्भों में जहां यह भ्रमित नहीं है, एक कोण को ऊपरी केस रोमन अक्षर द्वारा दर्शाया जा सकता है जो इसके शीर्ष को दर्शाता है। उदाहरण के लिए इस आलेख में आंकड़े देखें।

ज्यामितीय आकृतियों में, कोणों को उन तीन बिंदुओं से भी पहचाना जा सकता है जो उन्हें परिभाषित करते हैं। उदाहरण के लिए, एबी और एसी किरणों (अर्थात बिंदु ए से बिंदु बी और सी तक की रेखाएं) द्वारा गठित शीर्ष ए वाले कोण को दर्शाया गया है ∠BAC या ${\widehat {\rm {BAC}}}$. जहां भ्रम का कोई खतरा नहीं है, कोण को कभी-कभी केवल इसके शीर्ष (इस मामले में कोण ए) द्वारा संदर्भित किया जा सकता है।

संभावित रूप से, एक कोण के रूप में दर्शाया गया है, कहते हैं, ∠BAC, चार कोणों में से किसी को भी संदर्भित कर सकता है: बी से सी तक का दक्षिणावर्त कोण, बी से सी का वामावर्त कोण, सी से बी का दक्षिणावर्त कोण, या सी से बी का वामावर्त कोण, जहां कोण की दिशा है मापा इसका संकेत निर्धारित करता है (सकारात्मक और नकारात्मक कोण देखें)। हालांकि, कई ज्यामितीय स्थितियों में, यह संदर्भ से स्पष्ट है कि सकारात्मक कोण 180 डिग्री से कम या उसके बराबर है, ऐसी स्थिति में कोई अस्पष्टता नहीं होती है। अन्यथा, एक सम्मेलन अपनाया जा सकता है ताकि ∠BAC हमेशा बी से सी तक वामावर्त (सकारात्मक) कोण को संदर्भित करता है, और ∠CAB C से B तक वामावर्त (धनात्मक) कोण।

कोणों के प्रकार

"Oblique angle" redirects here. For the cinematographic technique, see Dutch angle.

व्यक्तिगत कोण

कोणों के लिए कुछ सामान्य शब्दावली है, जिसका माप हमेशा ऋणात्मक नहीं होता (देखें .)§ Positive and negative angles):* 0° के बराबर या मुड़े हुए कोण को शून्य कोण कहा जाता है।

• एक समकोण (90° से कम) से छोटे कोण को न्यून कोण (न्यून कोण का अर्थ तेज) कहा जाता है।
• के बराबर कोण 1/4बारी (90° or π/2 रेडियन) को समकोण कहा जाता है। समकोण बनाने वाली दो रेखाएँ सामान्य, ओर्थोगोनल या लंबवत कहलाती हैं।
• एक समकोण से बड़ा और एक सीधे कोण से छोटा (90° और 180° के बीच) कोण को अधिक कोण (अधिक अर्थ वाला कुंद) कहा जाता है।
• के बराबर कोण {sfrac|2}} मोड़ (180° or .) π रेडियन) को एक सीधा कोण कहा जाता है।
• एक सीधे कोण से बड़ा लेकिन एक मोड़ से कम (180° और 360° के बीच) कोण को प्रतिवर्त कोण कहा जाता है।
• 1 मोड़ के बराबर कोण (360° या 2 .)π रेडियन) को पूर्ण कोण, पूर्ण कोण, गोल कोण या पेरिगॉन कहा जाता है।
• ऐसा कोण जो समकोण का गुणज न हो, तिरछा कोण कहलाता है।

नाम, अंतराल और मापने की इकाइयाँ नीचे दी गई तालिका में दिखाई गई हैं:

Right angle

Acute (a), obtuse (b), and straight (c) angles. The acute and obtuse angles are also known as oblique angles.

Reflex angle

नाम	शून्य	तीव्र	समकोण	कुंठित	सीधा	पलटा हुआ	पेरिगोन
इकाई	मध्यान्तर
मोड़	0 turn	(0, 1/4) मोड़	{अब्रैप|1/4 मोड़}}	{अब्रैप|(1/4, 1/2) मोड़}}	{अब्रैप|1/2 मोड़}}	{अब्रैप|(1/2, 1) बारी}}	{अब्रैप|1 मोड़}}
कांति	{अब्रैप | 0 रेड}}	{अब्रैप|(0, 1/2π) रेड}}	{अब्रैप|1/2πरेड}}	{अब्रैप|(1/2π,π) रेड}}	{अब्रैप|πरेड}}	{अब्रैप|(π, 2π) रेड}}	{अब्रैप|2πरेड}}
डिग्री	0°	(0, 90)°	90°	(90, 180)°	180°	(180, 360)°	360°
गोन	0g|शैली = चौड़ाई:3em; | (0, 100)g|शैली = चौड़ाई:3em; | 100g|शैली = चौड़ाई:3em; | (100, 200)g|शैली = चौड़ाई:3em; | 200g|शैली = चौड़ाई:3em; | (200, 400)g|शैली =मैंने उससे वादा किया: चाचा; | 400g|-

तुल्यता कोण जोड़े

• समान माप वाले कोण (अर्थात समान परिमाण) समान या सर्वांगसम कहलाते हैं। एक कोण को उसके माप से परिभाषित किया जाता है और वह कोण की भुजाओं की लंबाई पर निर्भर नहीं होता है (उदाहरण के लिए सभी समकोण माप में बराबर होते हैं)।
• दो कोण जो टर्मिनल पक्षों को साझा करते हैं, लेकिन एक मोड़ के पूर्णांक गुणक द्वारा आकार में भिन्न होते हैं, कोटरमिनल कोण कहलाते हैं।
• एक संदर्भ कोण किसी भी कोण का तीव्र संस्करण है जिसे बार-बार घटाकर या सीधे कोण को जोड़कर निर्धारित किया जाता है (1/2 मोड़, 180°, या π रेडियन), जब तक आवश्यक हो, तब तक परिणाम का परिमाण एक न्यून कोण है, 0 और . के बीच का मान 1/4 मोड़, 90°, या π/2 रेडियन। उदाहरण के लिए, 30 डिग्री के कोण में 30 डिग्री का संदर्भ कोण होता है, और 150 डिग्री के कोण में 30 डिग्री (180-150) का संदर्भ कोण भी होता है। 750 डिग्री के कोण का संदर्भ कोण 30 डिग्री (750-720) होता है।

लंबवत और आसन्न कोण जोड़े

कोण समानता दिखाने के लिए यहां हैच के निशान का उपयोग किया जाता है।

और D ऊर्ध्वाधर कोणों का एक युग्म है। हैच_मार्क#कॉन्ग्रेंसी_नोटेशन|हैच के निशान यहां कोण समानता दिखाने के लिए उपयोग किए जाते हैं।

"Vertical angle" redirects here. Not to be confused with Zenith angle.

जब दो सीधी रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, तो चार कोण बनते हैं। जोड़ीवार इन कोणों को एक दूसरे के सापेक्ष उनके स्थान के अनुसार नाम दिया गया है।

• दो प्रतिच्छेदी सीधी रेखाओं से एक-दूसरे के सम्मुख कोणों का युग्म जो X-समान आकार बनाता है, ऊर्ध्व कोण या सम्मुख कोण या उर्ध्वाधर सम्मुख कोण कहलाते हैं। उन्हें vert के रूप में संक्षिप्त किया गया है। विपक्ष ई.एस.: उर्ध्वाधर सम्मुख कोणों की समानता को उर्ध्वाधर कोण प्रमेय कहते हैं। रोड्स के यूडेमस ने थेल्स ऑफ मिलेटस को सबूत के लिए जिम्मेदार ठहराया। प्रस्ताव ने दिखाया कि चूंकि दोनों लंबवत कोणों की एक जोड़ी दोनों आसन्न कोणों के पूरक हैं, लंबवत कोण माप में बराबर हैं। एक ऐतिहासिक नोट के अनुसार, जब थेल्स ने मिस्र का दौरा किया, तो उन्होंने देखा कि जब भी मिस्रवासी दो प्रतिच्छेद करने वाली रेखाएँ खींचते हैं, तो वे यह सुनिश्चित करने के लिए ऊर्ध्वाधर कोणों को मापते हैं कि वे समान हैं। थेल्स ने निष्कर्ष निकाला कि कोई यह साबित कर सकता है कि सभी ऊर्ध्वाधर कोण समान हैं यदि कोई कुछ सामान्य धारणाओं को स्वीकार करता है जैसे:

• सभी समकोण समान होते हैं।
• बराबर में जोड़े गए बराबर बराबर होते हैं।
• बराबर में से घटाए गए बराबर बराबर होते हैं।

जब दो आसन्न कोण एक सीधी रेखा बनाते हैं, तो वे संपूरक होते हैं। इसलिए, यदि हम यह मान लें कि कोण A का माप x के बराबर है, तो कोण C का माप होगा 180° − x. इसी प्रकार, कोण D की माप होगी 180° − x. कोण C और कोण D दोनों के माप . के बराबर हैं 180° − x और समरूप हैं। चूँकि कोण B दोनों कोणों C और D का पूरक है, कोण B के माप को निर्धारित करने के लिए इनमें से किसी भी कोण के माप का उपयोग किया जा सकता है। कोण C या कोण D के माप का उपयोग करके, हम कोण B के माप को ज्ञात करते हैं 180° − (180° − x) = 180° − 180° + x = x. इसलिए, कोण A और कोण B दोनों के माप x के बराबर हैं और माप में बराबर हैं।

कोण A और B आसन्न हैं।

• आसन्न कोण, अक्सर adj के रूप में संक्षिप्त। s, ऐसे कोण हैं जो एक सामान्य शीर्ष और किनारे साझा करते हैं लेकिन कोई आंतरिक बिंदु साझा नहीं करते हैं। दूसरे शब्दों में, वे कोण होते हैं जो अगल-बगल होते हैं, या आसन्न होते हैं, एक हाथ साझा करते हैं। आसन्न कोण जो एक समकोण, सीधे कोण या पूर्ण कोण के योग होते हैं, विशेष होते हैं और क्रमशः पूरक, पूरक और पूरक कोण कहलाते हैं (देखें।§ Combining angle pairsनीचे)।

एक तिर्यक रेखा एक रेखा है जो (अक्सर समानांतर) रेखाओं की एक जोड़ी को काटती है, और वैकल्पिक आंतरिक कोणों, संबंधित कोणों, आंतरिक कोणों और बाहरी कोणों से जुड़ी होती है।

कोण जोड़े का संयोजन

तीन विशेष कोण जोड़े में कोणों का योग शामिल होता है:

पूरक कोण a और b (b a और a का पूरक है। > b) का पूरक है।

• पूरक कोण कोण युग्म होते हैं जिनके मापों का योग एक समकोण होता है (1/4 मोड़, 90°, या π/2 रेडियन)।यदि दो पूरक कोण आसन्न हैं, तो उनकी गैर-साझा भुजाएँ एक समकोण बनाती हैं। यूक्लिडियन ज्यामिति में, एक समकोण त्रिभुज में दो न्यून कोण पूरक होते हैं, क्योंकि त्रिभुज के आंतरिक कोणों का योग 180 डिग्री होता है, और समकोण स्वयं 90 डिग्री का होता है।

विशेषण पूरक लैटिन पूरक से है, जो क्रिया पूर्ण से जुड़ा है, भरने के लिए। एक समकोण बनाने के लिए एक न्यून कोण इसके पूरक द्वारा भरा जाता है।

कोण और समकोण के बीच के अंतर को कोण का पूरक कहा जाता है।:यदि कोण A और B पूरक हैं, तो निम्नलिखित संबंध धारण करते हैं:

${\begin{aligned}&\sin ^{2}A+\sin ^{2}B=1&&\cos ^{2}A+\cos ^{2}B=1\\[3pt]&\tan A=\cot B&&\sec A=\csc B\end{aligned}}$

(एक कोण की स्पर्श रेखा उसके पूरक के कोटेंजेंट के बराबर होती है और उसकी छेदक उसके पूरक के कोसेकेंट के बराबर होती है।)

कुछ त्रिकोणमितीय अनुपातों के नामों में उपसर्ग सह-संपूरक शब्द को संदर्भित करता है।

कोण a और b संपूरक कोण हैं।

• दो कोण जो एक सीधे कोण का योग करते हैं (1/2 मोड़, 180°, या π रेडियन) संपूरक कोण कहलाते हैं।:यदि दो संपूरक कोण आसन्न हैं (अर्थात एक उभयनिष्ठ शीर्ष है और केवल एक भुजा साझा करते हैं), तो उनकी गैर-साझा भुजाएँ एक सीधी रेखा बनाती हैं। ऐसे कोणों को कोणों का रैखिक युग्म कहा जाता है। हालांकि, पूरक कोणों का एक ही रेखा पर होना जरूरी नहीं है, और उन्हें अंतरिक्ष में अलग किया जा सकता है। उदाहरण के लिए, समांतर चतुर्भुज के आसन्न कोण पूरक होते हैं, और चक्रीय चतुर्भुज के विपरीत कोण (जिसके शीर्ष सभी एक ही वृत्त पर पड़ते हैं) पूरक होते हैं।

यदि एक बिंदु P केंद्र O वाले वृत्त के बाहर है, और यदि P से स्पर्श रेखाएँ वृत्त को बिंदु T और Q पर स्पर्श करती हैं, तो TPQ और TOQ पूरक हैं।

संपूरक कोणों की ज्या बराबर होती है। उनके कोसाइन और स्पर्शरेखा (जब तक कि अपरिभाषित नहीं) परिमाण में बराबर होते हैं लेकिन विपरीत संकेत होते हैं।

यूक्लिडियन ज्यामिति में, त्रिभुज के दो कोणों का योग तीसरे का संपूरक होता है, क्योंकि त्रिभुज के आंतरिक कोणों का योग एक सरल कोण होता है।

दो पूरक कोणों का योग एक पूर्ण कोण होता है।

• दो कोण जो एक पूर्ण कोण का योग करते हैं (1 मोड़, 360°, या 2π रेडियन) को पूरक कोण या संयुग्म कोण कहा जाता है।

  एक कोण और एक पूर्ण कोण के बीच के अंतर को कोण का योग या कोण का संयुग्मी कहा जाता है।

बहुभुज-संबंधित कोण

आंतरिक और बाहरी कोण।

• एक कोण जो एक साधारण बहुभुज का भाग होता है, एक आंतरिक कोण कहलाता है यदि वह उस साधारण बहुभुज के अंदर स्थित हो। एक साधारण अवतल बहुभुज में कम से कम एक आंतरिक कोण होता है जो एक प्रतिवर्त कोण होता है।

  यूक्लिडियन ज्यामिति में, त्रिभुज के आंतरिक कोणों के मापों का योग होता है π रेडियन, 180°, or 1/2 मोड़; एक साधारण उत्तल चतुर्भुज के आंतरिक कोणों के माप 2 . तक जोड़ते हैंπ रेडियन, 360°, या 1 मोड़। सामान्य तौर पर, n भुजाओं वाले एक साधारण उत्तल बहुभुज के आंतरिक कोणों के मापों का योग (n − 2) होता है।πरेडियन, या (n − 2)180 डिग्री, (n − 2)2 समकोण, या (n − 2)1/2मोड़।

• एक आंतरिक कोण के पूरक को एक बाहरी कोण कहा जाता है, अर्थात एक आंतरिक कोण और एक बाहरी कोण कोणों का एक रैखिक युग्म बनाते हैं। बहुभुज के प्रत्येक शीर्ष पर दो बाहरी कोण होते हैं, जिनमें से प्रत्येक को शीर्ष पर मिलने वाले बहुभुज के दो पक्षों में से एक को विस्तारित करके निर्धारित किया जाता है; ये दो कोण लंबवत हैं और इसलिए बराबर हैं। एक बाहरी कोण बहुभुज का पता लगाने के लिए एक शीर्ष पर घूमने की मात्रा को मापता है। यदि संगत आंतरिक कोण प्रतिवर्त कोण है, तो बाह्य कोण को ऋणात्मक माना जाना चाहिए। यहां तक ​​कि एक गैर-साधारण बहुभुज में भी बाहरी कोण को परिभाषित करना संभव हो सकता है, लेकिन बाहरी कोण माप के संकेत को तय करने के लिए किसी को विमान (या सतह) का एक अभिविन्यास चुनना होगा।

  यूक्लिडियन ज्यामिति में, एक साधारण उत्तल बहुभुज के बाहरी कोणों का योग, यदि प्रत्येक शीर्ष पर दो बाहरी कोणों में से केवल एक माना जाता है, तो एक पूर्ण मोड़ (360°) होगा। यहाँ बाह्य कोण को पूरक बाह्य कोण कहा जा सकता है। नियमित बहुभुज बनाते समय बाहरी कोणों का उपयोग आमतौर पर लोगो कछुए कार्यक्रमों में किया जाता है।

• एक त्रिभुज में, दो बाह्य कोणों के समद्विभाजक और दूसरे आंतरिक कोण के समद्विभाजक समवर्ती होते हैं (एक बिंदु पर मिलते हैं)।
• एक त्रिभुज में, तीन प्रतिच्छेदन बिंदु, प्रत्येक बाहरी कोण का समद्विभाजक, जिसकी विपरीत विस्तारित भुजा होती है, संरेख होते हैं।
• एक त्रिभुज में, तीन प्रतिच्छेदन बिंदु, उनमें से दो एक आंतरिक कोण समद्विभाजक और विपरीत भुजा के बीच, और तीसरा बाहरी कोण समद्विभाजक और विस्तारित विपरीत भुजा के बीच, संरेख हैं।
• कुछ लेखक साधारण बहुभुज के बाहरी कोण के नाम का उपयोग केवल आंतरिक कोण के बाहरी कोण (पूरक नहीं!) के पूरक के लिए करते हैं।यह उपरोक्त उपयोग के साथ विरोध करता है।

समतल से संबंधित कोण

• दो तलों के बीच के कोण (जैसे एक बहुफलक के दो आसन्न फलक) को द्विफलकीय कोण कहा जाता है।इसे विमानों के लिए सामान्य दो रेखाओं के बीच तीव्र कोण के रूप में परिभाषित किया जा सकता है।
• एक समतल और एक प्रतिच्छेदी सीधी रेखा के बीच का कोण प्रतिच्छेदन रेखा और प्रतिच्छेदन बिंदु से जाने वाली रेखा के बीच के कोण को घटाकर नब्बे डिग्री के बराबर होता है और समतल के अभिलंबवत होता है।

== कोणों को मापना==एक ज्यामितीय कोण का आकार आमतौर पर सबसे छोटे रोटेशन के परिमाण की विशेषता होती है जो एक किरण को दूसरे में मैप करता है। समान आकार वाले कोणों को समान या सर्वांगसम या माप में बराबर कहा जाता है।

कुछ संदर्भों में, जैसे किसी वृत्त पर एक बिंदु की पहचान करना या किसी संदर्भ अभिविन्यास के सापेक्ष दो आयामों में किसी वस्तु के उन्मुखीकरण का वर्णन करना, कोण जो पूर्ण मोड़ के सटीक गुणक से भिन्न होते हैं, प्रभावी रूप से समतुल्य होते हैं। अन्य संदर्भों में, जैसे कि एक सर्पिल वक्र पर एक बिंदु की पहचान करना या किसी संदर्भ अभिविन्यास के सापेक्ष दो आयामों में किसी वस्तु के संचयी घुमाव का वर्णन करना, कोण जो एक पूर्ण मोड़ के गैर-शून्य गुणक से भिन्न होते हैं, समकक्ष नहीं होते हैं।

आर}} रेडियन}}।

θ है s/r रेडियन।

कोण को मापने के लिए θ, कोण के शीर्ष पर केन्द्रित एक वृत्ताकार चाप खींचा जाता है, उदा. कम्पास की एक जोड़ी के साथ। चाप की लंबाई s का वृत्त की त्रिज्या r से अनुपात कोण में रेडियन की संख्या है। परंपरागत रूप से, गणित में और SI में, रेडियन को आयामहीन मान 1 के बराबर माना जाता है।

कोण को व्यक्त किया गया एक और कोणीय इकाई तब कोण को फॉर्म के उपयुक्त रूपांतरण स्थिरांक से गुणा करके प्राप्त किया जा सकता है k/2π, जहाँ k चुनी हुई इकाई में व्यक्त एक पूर्ण मोड़ का माप है (उदाहरण के लिए, k = 360° डिग्री के लिए या स्नातक के लिए 400 ग्रेड):

$\theta ={\frac {k}{2\pi }}\cdot {\frac {s}{r}}.$

का मूल्य θ इस प्रकार परिभाषित वृत्त के आकार से स्वतंत्र है: यदि त्रिज्या की लंबाई बदल जाती है तो चाप की लंबाई उसी अनुपात में बदल जाती है, इसलिए अनुपात s/r अपरिवर्तित रहता है।

कोण जोड़ अभिधारणा

कोण योग अभिगृहीत बताता है कि यदि B कोण AOC के अभ्यंतर में है, तो

$m\angle \mathrm {AOC} =m\angle \mathrm {AOB} +m\angle \mathrm {BOC}$

कोण AOC का माप कोण AOB के माप और कोण BOC के माप का योग होता है।

इकाइयां

1 रेडियन की परिभाषा

Dian

पूरे इतिहास में, कोणों को विभिन्न इकाइयों में मापा गया है। इन्हें कोणीय इकाइयों के रूप में जाना जाता है, जिनमें सबसे समकालीन इकाइयाँ डिग्री (°), रेडियन (रेड), और ग्रेडियन (ग्रेड) हैं, हालाँकि कई अन्य का उपयोग पूरे इतिहास में किया गया है।

मात्राओं की अंतर्राष्ट्रीय प्रणाली में, कोण को एक आयामहीन मात्रा के रूप में परिभाषित किया गया है। यह प्रभावित करता है कि आयामी विश्लेषण में कोण का इलाज कैसे किया जाता है।

कोणीय माप की अधिकांश इकाइयाँ इस प्रकार परिभाषित की जाती हैं कि किसी पूर्ण संख्या n के लिए एक मोड़ (अर्थात एक पूर्ण वृत्त) n इकाइयों के बराबर होता है। रेडियन (और इसके दशमलव उपगुणक) और व्यास भाग दो अपवाद हैं।

एक रेडियन एक वृत्त के चाप द्वारा अंतरित कोण होता है जिसकी लंबाई वृत्त की त्रिज्या के समान होती है। रेडियन एसआई प्रणाली में कोणीय माप की व्युत्पन्न इकाई है। परिभाषा के अनुसार, यह आयामहीन है, हालांकि अस्पष्टता से बचने के लिए इसे रेड के रूप में निर्दिष्ट किया जा सकता है। डिग्री में मापे गए कोणों को ° के प्रतीक के साथ दिखाया जाता है। डिग्री के उपखंड मिनट हैं (प्रतीक ′, 1′ = 1/60°) और दूसरा (प्रतीक ″, 1″ = 1/3600°)। 360° का कोण एक पूर्ण वृत्त द्वारा अंतरित कोण के संगत होता है, और के बराबर होता है 2π रेडियन, या 400 ग्रेडियन।

कोणों को निरूपित करने के लिए प्रयुक्त अन्य इकाइयाँ निम्नलिखित तालिका में सूचीबद्ध हैं। इन इकाइयों को इस तरह परिभाषित किया गया है कि घुमावों की संख्या एक पूर्ण घूर्णन के बराबर है।

नाम	नंबर एक मोड़ में	डिग्री में	विवरण
टर्न	1	360°	2πरेडियन या 360 डिग्री।
के गुणज π	2	180°	के गुणज π रेडियन (MULπ) इकाई RPN वैज्ञानिक कैलकुलेटर WP 43S में लागू की गई है। यह भी देखें: IEEE 754 अनुशंसित संचालन
चतुर्थांश	4	90°	एक चतुर्थांश a . है 1/4मोड़ और एक समकोण के रूप में भी जाना जाता है। चतुर्थांश यूक्लिड के तत्वों में प्रयुक्त इकाई है। जर्मन में, प्रतीक ∟चतुर्भुज को निरूपित करने के लिए प्रयोग किया गया है। 1 क्वाड = 90° = π/2 रेड = 1/4 बारी = 100 ग्रेड।
सेक्सटेंट	6	60°	सेक्सटेंट वह इकाई थी जिसका इस्तेमाल बेबीलोन के लोग करते थे, डिग्री, चाप का मिनट और चाप का दूसरा भाग बेबीलोनियाई इकाई की सेक्सेजिमल सबयूनिट हैं। शासक और परकार के साथ निर्माण करना विशेष रूप से आसान है। यह समबाहु त्रिभुज का कोण है या is 1/6मोड़। 1 बेबीलोन की इकाई = 60° = π/ 3 रेड 1.047197551 रेड।	-	2π	57°17′	रेडियन एक वृत्त की परिधि से निर्धारित होता है जो वृत्त की त्रिज्या के बराबर लंबाई (n = 2) हैπ= 6.283...)। यह एक वृत्त के चाप द्वारा अंतरित कोण होता है जिसकी लंबाई वृत्त की त्रिज्या के समान होती है। रेडियन का प्रतीक रेड है। एक मोड़ 2 . हैπरेडियन, और एक रेडियन है 180°/π, या लगभग 57.2958 डिग्री। गणितीय ग्रंथों में कोण o . होते हैंften को एक के बराबर रेडियन के साथ आयामहीन माना जाता है, जिसके परिणामस्वरूप यूनिट रेड को अक्सर छोड़ दिया जाता है। रेडियन का उपयोग व्यावहारिक ज्यामिति से परे लगभग सभी गणितीय कार्यों में किया जाता है, उदाहरण के लिए, मनभावन और प्राकृतिक गुणों के कारण जो त्रिकोणमितीय कार्य प्रदर्शित करते हैं जब उनके तर्क रेडियन में होते हैं। रेडियन एसआई में कोणीय माप की (व्युत्पन्न) इकाई है, जो कोण को आयामहीन भी मानता है।
Hexacontade	6°	हेक्साकॉन्टेड एक इकाई है जिसका उपयोग इरेटोस्थनीज द्वारा किया जाता है। यह 6° के बराबर होता है, जिससे एक पूरा मोड़ 60 हेक्साकॉन्टेड्स में विभाजित हो जाता है।
बाइनरी डिग्री	256	1°33'45	बाइनरी डिग्री, जिसे बाइनरी रेडियन या ब्रैड या बाइनरी कोणीय माप (BAM) के रूप में भी जाना जाता है।बाइनरी डिग्री का उपयोग कंप्यूटिंग में किया जाता है ताकि एक कोण को एक बाइट में कुशलता से दर्शाया जा सके (यद्यपि सीमित परिशुद्धता के लिए)। कंप्यूटिंग में प्रयुक्त कोण के अन्य उपाय एक पूरे मोड़ को 2 . में विभाजित करने पर आधारित हो सकते हैंnn के अन्य मानों के लिए समान भाग। यह है 1/256 एक मोड़ का।|-	डिग्री	360	1°	इस पुराने सेक्जेसिमल सबयूनिट का एक फायदा यह है कि साधारण ज्यामिति में आम कई कोणों को डिग्री की एक पूरी संख्या के रूप में मापा जाता है। डिग्री के अंश सामान्य दशमलव अंकन में लिखे जा सकते हैं (उदाहरण के लिए साढ़े तीन डिग्री के लिए 3.5 डिग्री), लेकिन डिग्री-मिनट-सेकंड सिस्टम की मिनट और दूसरी सेक्सेजिमल सब यूनिट भी उपयोग में हैं, खासकर भौगोलिक निर्देशांक और खगोल विज्ञान में और बैलिस्टिक (n = 360) एक छोटे सुपरस्क्रिप्ट सर्कल (°) द्वारा दर्शाई गई डिग्री, एक मोड़ का 1/360 है, इसलिए एक मोड़ 360° है। पहले दिए गए सूत्र के लिए डिग्री का मामला, k = . सेट करके n = 360° इकाइयों की एक डिग्री प्राप्त की जाती है 360°/2π.
ग्रैड	400	0°54′	ग्रेड, जिसे ग्रेड, ग्रेडियन या गॉन भी कहा जाता है। यह चतुर्थांश की दशमलव उपइकाई है। एक समकोण 100 ग्रैड है। एक किलोमीटर को ऐतिहासिक रूप से पृथ्वी के एक मध्याह्न रेखा के साथ चाप के एक सेंटी-ग्रेड के रूप में परिभाषित किया गया था, इसलिए किलोमीटर सेक्सजेसिमल नॉटिकल मील (n = 400) का दशमलव एनालॉग है। ग्रेड का उपयोग ज्यादातर त्रिभुज और महाद्वीपीय सर्वेक्षण में किया जाता है।
21,600	0°1′	चाप का मिनट (या एमओए, आर्कमिन्यूट, या बस मिनट) है 1/60 एक डिग्री का। एक समुद्री मील को ऐतिहासिक रूप से पृथ्वी के एक बड़े वृत्त (n = 21,600) के साथ चाप के एक मिनट के रूप में परिभाषित किया गया था। आर्कमिन्यूट है 1/60 डिग्री का = 1/21,600 मोड़। इसे एक अभाज्य ( ′ ) द्वारा निरूपित किया जाता है। उदाहरण के लिए, 3° 30′ 3 × 60 + 30 = 210 मिनट या 3 + के बराबर है30/60 = 3.5 डिग्री। कभी-कभी दशमलव अंशों के साथ मिश्रित प्रारूप का भी उपयोग किया जाता है, उदा। 3° 5.72′ = 3 +5.72/60 डिग्री। एक समुद्री मील को ऐतिहासिक रूप से पृथ्वी के एक महान वृत्त के साथ एक आर्कमिन्यूट के रूप में परिभाषित किया गया था।
1,296,000	0°0′1″	आर्क का दूसरा (या आर्कसेकंड, या सिर्फ दूसरा) है 1/60 चाप के एक मिनट और 1/3600 एक डिग्री का (n = 1,296,000)। आर्कसेकंड (या चाप का दूसरा, या सिर्फ दूसरा) है 1/60 एक चापाकल का और 1/3600 एक डिग्री का। इसे दोहरे अभाज्य ( ″ ) से निरूपित किया जाता है। उदाहरण के लिए, 3° 7′ 30″ 3 + . के बराबर है 7/60 + 30/3600 डिग्री, या 3.125 डिग्री।

अन्य वर्णनकर्ता

• घंटे का कोण (n = 24): खगोलीय घंटे का कोण है 1/24मोड़। चूंकि यह प्रणाली उन वस्तुओं को मापने के लिए उत्तरदायी है जो प्रति दिन एक बार चक्र करते हैं (जैसे सितारों की सापेक्ष स्थिति), सेक्सेजिमल सबयूनिट्स को मिनट का समय और दूसरा समय कहा जाता है। ये चाप के मिनट और सेकंड से अलग और 15 गुना बड़े हैं। 1 घंटे = 15° = π/12 रेड = 1/6क्वाड = 1/24बारी = 16+2/3ग्रेड।
• (कम्पास) बिंदु या हवा (n = 32): नेविगेशन में उपयोग किया जाने वाला बिंदु है 1/32 एक मोड़ का। 1 बिंदु = 1/8 समकोण का = 11.25° = 12.5 ग्रेड। प्रत्येक बिंदु को चार तिमाही-अंकों में विभाजित किया जाता है ताकि 1 मोड़ 128 तिमाही-अंक के बराबर हो।
• Pechus (n = 144–180): Pechus एक बेबीलोनियाई इकाई थी जो लगभग 2° या बराबर थी 2+1/2°.
• ताऊ, एक चक्कर में रेडियन की संख्या (1 मोड़ = τ रेड), τ = 2π.
• व्यास वाला हिस्सा (n = 376.99...): व्यास वाला हिस्सा (कभी-कभी इस्लामी गणित में इस्तेमाल होता है) है 1/60 रेडियन एक व्यास वाला भाग लगभग 0.95493° होता है। प्रति मोड़ लगभग 376.991 व्यास के हिस्से हैं।
• मिलीराडियन और व्युत्पन्न परिभाषाएँ: सच्चे मिलिरेडियन को एक रेडियन के हज़ारवें हिस्से को परिभाषित किया जाता है, जिसका अर्थ है कि एक मोड़ का रोटेशन ठीक 2000π मिल (या लगभग 6283.185 मील) के बराबर होगा, और आग्नेयास्त्रों के लिए लगभग सभी स्कोप जगहें इस परिभाषा के लिए कैलिब्रेटेड हैं। इसके अलावा तोपखाने और नेविगेशन के लिए इस्तेमाल की जाने वाली तीन अन्य व्युत्पन्न परिभाषाएँ हैं जो लगभग एक मिलीरेडियन के बराबर हैं। इन तीन अन्य परिभाषाओं के तहत एक मोड़ ठीक 6000, 6300 या 6400 मील के लिए बनाता है, जो 0.05625 से 0.06 डिग्री (3.375 से 3.6 मिनट) तक की सीमा के बराबर है। इसकी तुलना में, वास्तविक मिलीरेडियन लगभग 0.05729578 डिग्री (3.43775 मिनट) है। एक नाटो सैन्य को परिभाषित किया गया है 1/6400 एक वृत्त का। ट्रू मिलिरेडियन की तरह ही, अन्य सभी परिभाषाएं मिल की सबटेंशन की उपयोगी संपत्ति का फायदा उठाती हैं, यानी कि एक मिलीरेडियन का मान लगभग 1 मीटर की चौड़ाई से घटाए गए कोण के बराबर होता है जैसा कि 1 किमी दूर से देखा जाता है (2π/6400 = 0.0009817... ≈ {स्फ्रैक|1000}})।
• अखनाम और ज़म। पुराने अरब में एक मोड़ को 32 अखनाम में विभाजित किया गया था और प्रत्येक अखनाम को 7 ज़म में विभाजित किया गया था, ताकि एक मोड़ 224 ज़म हो।

हस्ताक्षरित कोण

See also: Sign (mathematics) § Angles

हालांकि एक कोण के मापन की परिभाषा एक नकारात्मक कोण की अवधारणा का समर्थन नहीं करती है, यह अक्सर एक सम्मेलन को लागू करने के लिए उपयोगी होता है जो सकारात्मक और नकारात्मक कोणीय मूल्यों को कुछ संदर्भ के सापेक्ष विपरीत दिशाओं में अभिविन्यास और/या घुमावों का प्रतिनिधित्व करने की अनुमति देता है।

द्वि-आयामी कार्टेशियन समन्वय प्रणाली में, एक कोण को आमतौर पर इसके दो पक्षों द्वारा परिभाषित किया जाता है, इसके शीर्ष पर मूल। प्रारंभिक पक्ष सकारात्मक एक्स-अक्ष पर है, जबकि दूसरी तरफ या टर्मिनल पक्ष रेडियन, डिग्री या मोड़ में प्रारंभिक पक्ष से माप द्वारा परिभाषित किया गया है। धनात्मक कोणों के साथ धनात्मक y-अक्ष की ओर घूर्णन और ऋणात्मक y-अक्ष की ओर घूर्णन का प्रतिनिधित्व करने वाले ऋणात्मक कोण। जब कार्टेशियन निर्देशांक मानक स्थिति द्वारा दर्शाए जाते हैं, जो x-अक्ष दाईं ओर और y-अक्ष ऊपर की ओर परिभाषित होते हैं, सकारात्मक घुमाव वामावर्त होते हैं और नकारात्मक घुमाव दक्षिणावर्त होते हैं।

कई संदर्भों में, −θ का कोण प्रभावी रूप से एक पूर्ण मोड़ माइनस के कोण के बराबर होता है। उदाहरण के लिए, −45° के रूप में दर्शाया गया एक अभिविन्यास प्रभावी रूप से 360° − 45° या 315° के रूप में दर्शाए गए अभिविन्यास के बराबर होता है। हालांकि अंतिम स्थिति समान है, -45° का एक भौतिक घुमाव (आंदोलन) 315° के घूर्णन के समान नहीं है (उदाहरण के लिए, धूल भरे फर्श पर झाड़ू रखने वाले व्यक्ति के घूमने से अलग-अलग निशान दिखाई देंगे फर्श पर बह क्षेत्रों की)।

त्रि-आयामी ज्यामिति में, दक्षिणावर्त और वामावर्त का कोई पूर्ण अर्थ नहीं होता है, इसलिए सकारात्मक और नकारात्मक कोणों की दिशा को कुछ संदर्भ के सापेक्ष परिभाषित किया जाना चाहिए, जो आमतौर पर कोण के शीर्ष से गुजरने वाला एक वेक्टर होता है और उस विमान के लंबवत होता है जिसमें की किरणें होती हैं कोण झूठ।

नेविगेशन में, बियरिंग्स या अज़ीमुथ को उत्तर के सापेक्ष मापा जाता है। परंपरा के अनुसार, ऊपर से देखने पर, असर कोण सकारात्मक दक्षिणावर्त होते हैं, इसलिए 45° का असर उत्तर-पूर्व अभिविन्यास से मेल खाता है। नेविगेशन में नेगेटिव बियरिंग्स का उपयोग नहीं किया जाता है, इसलिए उत्तर-पश्चिम ओरिएंटेशन 315° के बेयरिंग से मेल खाता है।

कोण के आकार को मापने के वैकल्पिक तरीके

एक कोणीय इकाई के लिए, यह निश्चित है कि कोण जोड़ अभिधारणा धारण करता है। कुछ कोण माप जहां कोण जोड़ अभिधारणा धारण नहीं करते हैं उनमें शामिल हैं:

• ढलान या ढाल कोण के स्पर्शरेखा के बराबर है; एक ढाल को अक्सर प्रतिशत के रूप में व्यक्त किया जाता है। बहुत छोटे मान (5% से कम) के लिए, ढलान का ग्रेड लगभग रेडियन में कोण का माप होता है।
• दो रेखाओं के बीच के फैलाव को परिमेय ज्यामिति में रेखाओं के बीच के कोण की ज्या के वर्ग के रूप में परिभाषित किया जाता है। चूँकि किसी कोण की ज्या और उसके संपूरक कोण की ज्या समान होती है, कोई भी घूर्णन कोण जो किसी एक रेखा को दूसरी रेखा में मैप करता है, रेखाओं के बीच फैलाव के लिए समान मान की ओर ले जाता है।
• हालांकि शायद ही कभी किया जाता है, कोई त्रिकोणमितीय कार्यों के प्रत्यक्ष परिणामों की रिपोर्ट कर सकता है, जैसे कोण की साइन।

खगोलीय अनुमान

Main article: Angular diameter

खगोलविद वस्तुओं के स्पष्ट आकार और उनके बीच की दूरी को उनके अवलोकन बिंदु से डिग्री में मापते हैं।

• 0.5° पृथ्वी से देखे गए सूर्य या चंद्रमा का अनुमानित व्यास है।
• 1° हाथ की लंबाई पर छोटी उंगली की अनुमानित चौड़ाई है।
• 10° बांह की लंबाई पर बंद मुट्ठी की अनुमानित चौड़ाई है।
• 20° हाथ की लंबाई पर एक हैंड्सपैन की अनुमानित चौड़ाई है।

ये माप स्पष्ट रूप से व्यक्तिगत विषय पर निर्भर करते हैं, और उपरोक्त को केवल अंगूठे के अनुमान के मोटे नियम के रूप में माना जाना चाहिए।

खगोल विज्ञान में, दाएं उदगम और गिरावट को आमतौर पर कोणीय इकाइयों में मापा जाता है, जो कि 24 घंटे के दिन के आधार पर समय के संदर्भ में व्यक्त किया जाता है।

Unit	Symbol	Degree	Radians	Circle	Other
Hour	h	15°	π⁄12	1⁄24
Minute	m	0°15′	π⁄720	1⁄1,440	1⁄60 hour
Second	s	0°0′15″	π⁄43200	1⁄86,400	1⁄60 minute

वक्रों के बीच कोण

P पर दो वक्रों के बीच के कोण को P पर स्पर्शरेखा A और B के बीच के कोण के रूप में परिभाषित किया गया है।

एक रेखा और एक वक्र (मिश्रित कोण) या दो प्रतिच्छेदन वक्रों (वक्रीय कोण) के बीच के कोण को प्रतिच्छेदन बिंदु पर स्पर्शरेखा के बीच के कोण के रूप में परिभाषित किया गया है। विशेष मामलों को विभिन्न नाम (अब शायद ही कभी, यदि कभी इस्तेमाल किया जाता है) दिए गए हैं: - एम्फीसिर्टिक (जीआर। ἀμφί, दोनों तरफ, , उत्तल) या cissoidal (Gr. , ivy), उभयलिंगी; xystroidal या cystroidal (Gr। , स्क्रैपिंग के लिए एक उपकरण), अवतल-उत्तल; एम्फीकोएलिक (जीआर। , एक खोखला) या एंगुलस लुन्युलरिस, बीकोन्केव।

समद्विभाजक और समद्विभाजक कोण

Main articles: Bisection § Angle bisector, and Angle trisection

प्राचीन यूनानी गणितज्ञ केवल एक कंपास और स्ट्रेटेज का उपयोग करके एक कोण को द्विभाजित करना (इसे समान माप के दो कोणों में विभाजित करना) जानते थे, लेकिन केवल कुछ कोणों को ही काट सकते थे। 1837 में, पियरे वॉन्टजेल ने दिखाया कि अधिकांश कोणों के लिए यह निर्माण नहीं किया जा सकता है।

डॉट उत्पाद और सामान्यीकरण

यूक्लिडियन अंतरिक्ष में, दो यूक्लिडियन वैक्टर 'u' और 'v' के बीच का कोण उनके डॉट उत्पाद और उनकी लंबाई से संबंधित है।

$\mathbf {u} \cdot \mathbf {v} =\cos(\theta )\left\|\mathbf {u} \right\|\left\|\mathbf {v} \right\|.$

यह सूत्र दो विमानों (या घुमावदार सतहों) के बीच के कोण को उनके सामान्य वैक्टर से और उनके वेक्टर समीकरणों से तिरछी रेखाओं के बीच के कोण को खोजने के लिए एक आसान विधि प्रदान करता है।

आंतरिक उत्पाद

एक अमूर्त वास्तविक आंतरिक उत्पाद स्थान में कोणों को परिभाषित करने के लिए, हम यूक्लिडियन डॉट उत्पाद ( · ) को आंतरिक उत्पाद से बदलते हैं $\langle \cdot ,\cdot \rangle$, अर्थात

$\langle \mathbf {u} ,\mathbf {v} \rangle =\cos(\theta )\ \left\|\mathbf {u} \right\|\left\|\mathbf {v} \right\|.$

एक जटिल आंतरिक उत्पाद स्थान में, उपरोक्त कोसाइन के लिए अभिव्यक्ति गैर-वास्तविक मान दे सकती है, इसलिए इसे इसके साथ बदल दिया जाता है

$\operatorname {Re} \left(\langle \mathbf {u} ,\mathbf {v} \rangle \right)=\cos(\theta )\left\|\mathbf {u} \right\|\left\|\mathbf {v} \right\|.$

या, अधिक सामान्यतः, निरपेक्ष मान का उपयोग करते हुए

$\left|\langle \mathbf {u} ,\mathbf {v} \rangle \right|=\left|\cos(\theta )\right|\left\|\mathbf {u} \right\|\left\|\mathbf {v} \right\|.$

बाद की परिभाषा वैक्टर की दिशा की उपेक्षा करती है और इस प्रकार एक-आयामी उप-स्थानों के बीच के कोण का वर्णन करती है $\operatorname {span} (\mathbf {u} )$ तथा $\operatorname {span} (\mathbf {v} )$ वैक्टर द्वारा फैला हुआ $\mathbf {u}$ तथा $\mathbf {v}$ अनुरूप।

उप-स्थानों के बीच कोण

एक-आयामी उप-स्थानों के बीच कोण की परिभाषा $\operatorname {span} (\mathbf {u} )$ तथा $\operatorname {span} (\mathbf {v} )$ के द्वारा दिया गया

$\left|\langle \mathbf {u} ,\mathbf {v} \rangle \right|=\left|\cos(\theta )\right|\left\|\mathbf {u} \right\|\left\|\mathbf {v} \right\|$

हिल्बर्ट अंतरिक्ष में किसी भी परिमित आयाम के उप-स्थानों तक बढ़ाया जा सकता है। दो उप-स्थान दिए गए हैं ${\mathcal {U}}$, ${\mathcal {W}}$ साथ $\dim({\mathcal {U}}):=k\leq \dim({\mathcal {W}}):=l$, यह की परिभाषा की ओर जाता है $k$ उप-स्थानों के बीच के कोणों को विहित या प्रमुख कोण कहा जाता है।

रीमैनियन ज्यामिति में कोण

रीमैनियन ज्यामिति में, दो स्पर्शरेखाओं के बीच के कोण को परिभाषित करने के लिए मीट्रिक टेंसर का उपयोग किया जाता है। जहाँ U और V स्पर्शरेखा सदिश हैं और g_ijमीट्रिक टेंसर G के घटक हैं,

$\cos \theta ={\frac {g_{ij}U^{i}V^{j}}{\sqrt {\left|g_{ij}U^{i}U^{j}\right|\left|g_{ij}V^{i}V^{j}\right|}}}.$

अतिपरवलयिक कोण

एक अतिपरवलयिक कोण एक अतिपरवलयिक फलन का तर्क है जिस प्रकार वृत्ताकार कोण एक वृत्तीय फलन का तर्क है। तुलना को एक अतिपरवलयिक क्षेत्र और एक वृत्ताकार क्षेत्र के उद्घाटन के आकार के रूप में देखा जा सकता है क्योंकि इन क्षेत्रों के क्षेत्र प्रत्येक मामले में कोण परिमाण के अनुरूप होते हैं। वृत्ताकार कोण के विपरीत, अतिपरवलयिक कोण असीम होता है। जब सर्कुलर और हाइपरबॉलिक फ़ंक्शंस को उनके कोण तर्क में अनंत श्रृंखला के रूप में देखा जाता है, तो सर्कुलर वाले हाइपरबॉलिक फ़ंक्शंस के केवल वैकल्पिक श्रृंखला रूप होते हैं। दो प्रकार के कोण और कार्य के इस बुनाई को लियोनहार्ड यूलर द्वारा अनंत के विश्लेषण के परिचय में समझाया गया था।

भूगोल और खगोल विज्ञान में कोण

भूगोल में, भौगोलिक समन्वय प्रणाली का उपयोग करके पृथ्वी पर किसी भी बिंदु के स्थान की पहचान की जा सकती है। यह प्रणाली भूमध्य रेखा और (आमतौर पर) ग्रीनविच मेरिडियन को संदर्भ के रूप में उपयोग करते हुए, पृथ्वी के केंद्र में अंतरित कोणों के संदर्भ में किसी भी स्थान के अक्षांश और देशांतर को निर्दिष्ट करती है।

खगोल विज्ञान में, खगोलीय क्षेत्र पर एक दिए गए बिंदु (अर्थात, एक खगोलीय वस्तु की स्पष्ट स्थिति) को कई खगोलीय समन्वय प्रणालियों में से किसी का उपयोग करके पहचाना जा सकता है, जहां संदर्भ विशेष प्रणाली के अनुसार भिन्न होते हैं। खगोलविद पृथ्वी के केंद्र के माध्यम से दो रेखाओं की कल्पना करके दो तारों के कोणीय पृथक्करण को मापते हैं, प्रत्येक एक तारे को काटता है। उन रेखाओं के बीच के कोण को मापा जा सकता है और यह दो तारों के बीच कोणीय पृथक्करण है।

भूगोल और खगोल विज्ञान दोनों में, देखने की दिशा को एक ऊर्ध्वाधर कोण के रूप में निर्दिष्ट किया जा सकता है जैसे कि क्षितिज के संबंध में ऊंचाई/ऊंचाई के साथ-साथ उत्तर के संबंध में दिगंश।

खगोलविद वस्तुओं के स्पष्ट आकार को कोणीय व्यास के रूप में भी मापते हैं। उदाहरण के लिए, जब पृथ्वी से देखा जाता है, तो पूर्णिमा का कोणीय व्यास लगभग 0.5° होता है। कोई कह सकता है, चंद्रमा का व्यास आधा डिग्री का कोण घटाता है। इस तरह के कोणीय माप को दूरी/आकार अनुपात में बदलने के लिए छोटे-कोण सूत्र का उपयोग किया जा सकता है।

यह भी देखें

• कोण मापने वाला यंत्र
• कोणीय आँकड़े (माध्य, मानक विचलन)
• कोण द्विभाजक
• कोणीय त्वरण
• कोणीय व्यास
• कोणीय गति
• तर्क (जटिल विश्लेषण)
• ज्योतिषीय पहलू
• केंद्रीय कोण
• घड़ी कोण की समस्या
• दशमलव डिग्री
• डायहेड्रल कोण
• बाहरी कोण प्रमेय
• सुनहरा कोण
• महान सर्कल दूरी
• खुदा हुआ कोण
• अपरिमेय कोण
• चरण (लहरें)
• चाँदा
• ठोस कोण
• गोलाकार कोण
• उत्कृष्ट कोण
• ट्राइसेक्शन
• जेनिथ कोण

ग्रंथ सूची

• Henderson, David W.; Taimina, Daina (2005), Experiencing Geometry / Euclidean and Non-Euclidean with History (3rd ed.), Pearson Prentice Hall, p. 104, ISBN 978-0-13-143748-7
• Heiberg, Johan Ludvig (1908), Heath, T. L. (ed.), Euclid, The Thirteen Books of Euclid's Elements, vol. 1, Cambridge: Cambridge University Press.
• Sidorov, L. A. (2001) [1994], "Angle", Encyclopedia of Mathematics, EMS Press
• Jacobs, Harold R. (1974), Geometry, W. H. Freeman, pp. 97, 255, ISBN 978-0-7167-0456-0
• Slocum, Jonathan (2007), Preliminary Indo-European lexicon — Pokorny PIE data, University of Texas research department: linguistics research center, retrieved 2 Feb 2010
• Shute, William G.; Shirk, William W.; Porter, George F. (1960), Plane and Solid Geometry, American Book Company, pp. 25–27
• Wong, Tak-wah; Wong, Ming-sim (2009), "Angles in Intersecting and Parallel Lines", New Century Mathematics, vol. 1B (1 ed.), Hong Kong: Oxford University Press, pp. 161–163, ISBN 978-0-19-800177-5

This article incorporates text from a publication now in the public domain: Chisholm, Hugh, ed. (1911), "Angle", Encyclopædia Britannica (in English), vol. 2 (11th ed.), Cambridge University Press, p. 14

बाहरी संबंध

• "Angle" , Encyclopædia Britannica, vol. 2 (9th ed.), 1878, pp. 29–30