ट्रांसवर्सल (इंस्ट्रूमेंट मेकिंग)
ट्रांसवर्सल (अनुप्रस्थ) वैज्ञानिक उपकरण पर एक ज्यामितीय निर्माण है जो एक स्नातक (साधन) को स्पष्टता की उन्नत स्तर तक पढ़ने की अनुमति देता है। आधुनिक समय में तिर्यक रेखाओं का स्थान वर्नियर पैमानों ने ले लिया है। यह विधि अवरोधन प्रमेय (जिसे थेल्स प्रमेय के रूप में भी जाना जाता है) पर आधारित है।
इतिहास
ट्रांसवर्सल (अनुप्रस्थ) का उपयोग ऐसे समय में किया जाता था, जब बारीकी से तैयार किए गए उपकरणों को बनाना जटिल होता था। वे 14वीं शताब्दी की प्रारंभ में उपकरणों पर पाए गए थे, किन्तु आविष्कारक अज्ञात है। 1342 में लेवी बेन गर्सन ने जैकब के कर्मचारियों (जाहिरा तौर पर जैकब बेन मकीर द्वारा पिछली शताब्दी का आविष्कार किया) नामक एक उपकरण प्रस्तुत किया और वर्णित उपकरण पर प्रयुक्त अनुप्रस्थ पैमाने की विधि का वर्णन किया।[1][2] थॉमस डिग्स ने गलती से ट्रांसवर्सल (अनुप्रस्थ) पैमाने की खोज का श्रेय मार्ग निर्देशक और खोजकर्ता रिचर्ड चांसलर को दिया (कुछ लेखकों द्वारा उनमें से: रिचर्ड चांसलर या रिचर्ड कांट्ज़लर को वॉचमेकर और अन्य नामों के साथ उद्धृत किया गया ।)[3][4][5][6][7][8] खगोलीय उपकरणों पर इसका उपयोग केवल 16वीं शताब्दी के अंत में प्रारंभ हुआ। टाइको ब्राहे ने उनका उपयोग किया और विधि को लोकप्रिय बनाने के लिए बहुत कुछ किया।[9][10] 18 वीं शताब्दी के अंत में एक बार पियरे-वर्नियर द्वारा विधि प्रस्तुत करने के बाद एक बार वर्नियर के आम हो जाने के बाद विधि समाप्त होने लगी।
ट्रांसवर्सल्स (अनुप्रस्थ) और वर्नियर पैमाने के बीच अंतरिम में, पेड्रो नून्स द्वारा विकसित नॉनियस (गणित में पैमानों को अंशांकित करने वाला यंत्र) प्रणाली का उपयोग किया गया था। यद्यपि, यह कभी भी सामान्य उपयोग में नहीं था। टायको ने भी नॉनियस (गणित में पैमानों को अंशांकित करने वाला यंत्र) विधियों का उपयोग किया, किन्तु ऐसा करने वाले वे एकमात्र प्रमुख खगोलशास्त्री प्रतीत होते हैं।
अनुप्रस्थ रैखिक
रेखीय अंशांकन पर रेखीय अनुप्रस्थ का उपयोग किया जाता था। रेखीय अंशांकन के तुरंत बाद रेखाओं की एक ग्रिड (जाल) का निर्माण किया गया था। ग्रेजुएशन के ऊपर फैली लाइनें ग्रिड का हिस्सा बनती हैं। ग्रिड में विस्तारित ग्रेजुएशन रेखाओं के लम्बवत् रेखाओं की संख्या उपकरण निर्माता द्वारा प्रदान की जाने वाली सूक्ष्मता की स्तर पर निर्भर थी।
पांच पंक्तियों का एक ग्रिड स्नातक स्तर की पढ़ाई के एक-पांचवें हिस्से के उपाय के निर्धारण की अनुमति देगा। एक दस-पंक्ति ग्रिड दसवें को मापने की अनुमति देगा। रेखाओं के बीच की दूरी तब तक महत्वपूर्ण नहीं है जब तक कि दूरी ठीक एक समान है। अधिक दूरी अधिक स्पष्टता के लिए बनाती है।
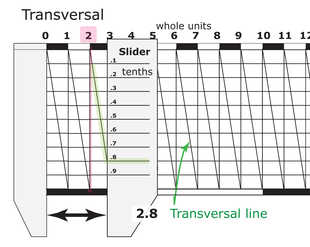
जैसा कि दाईं ओर के चित्रण में देखा गया है, एक बार जब ग्रिड को लिखा गया था, तो विकर्णों (अनुप्रस्थ रेखाओं) को ग्रिड में एक स्तंभ के सबसे ऊपरी कोने से विपरीत सबसे निचले कोने तक लिखा गया था। यह रेखा ग्रिड में क्रॉस रेखाओं को बराबर अंतराल में काटती है। एक कर्सर,असलियत या माप के समान संकेतक का उपयोग करके, निकटतम बिंदु जहां ट्रांसवर्सल (अनुप्रस्थ) ग्रिड को पार करता है, निर्धारित किया जाता है। यह माप के लिए ग्रेजुएशन के अंश को इंगित करता है।
दृष्टांत में, पठन को लंबवत लाल रेखा द्वारा इंगित किया गया है। यह एक एलाइडेड या इसी तरह के उपकरण का किनारा हो सकता है। चूंकि कर्सर ऊपर से चौथी ग्रिड लाइन के निकटतम ट्रांसवर्सल (अनुप्रस्थ) को पार करता है, रीडिंग (बाएं सबसे लंबी ग्रेजुएशन लाइन 0.0 है) 0.54 है।
सर्कुलर ट्रांसवर्सल्स (अनुप्रस्थ)
वृत्ताकार तिर्यक रेखाएँ रेखीय वाले के समान कार्य करती हैं किन्तु वृत्ताकार चापों के लिए। इस स्थितियोंे में, ग्रिड का निर्माण अधिक अधिक जटिल है। एक आयताकार ग्रिड काम नहीं करेगा। रेडियल रेखाओं और परिधि वाले चापों का एक ग्रिड बनाया जाना चाहिए। इसके अतिरिक्त, एक रेखीय अनुप्रस्थ रेखा रेडियल ग्रिड को समान खंडों में विभाजित नहीं करेगी। सही अनुपात प्रदान करने के लिए सर्कुलर आर्क सेगमेंट को ट्रांसवर्सल्स (अनुप्रस्थ) के रूप में बनाया जाना चाहिए।
टायको ब्राहे
टायको ब्राहे ने चाप के दो समूहों के बीच छेदक के साथ बनाई गई अनुप्रस्थ रेखाओं का एक ग्रिड बनाया जो दो अंशांकित अंगों का निर्माण करता है। दूसरे अंग के अगले विभाजन के साथ एक अंग के विभाजन को जोड़कर छेदक खींचे जाते हैं, और इसी तरह (2 मीटर त्रिज्या के टायको ब्राहे के चतुर्भुज के 2 स्तर के आवर्धन के साथ चित्र देखें)।[9]
उन्होंने प्रत्येक स्तर के लिए, एक V बनाने वाले एक वैकल्पिक मोड में छह सीधे ट्रांसवर्सल (अनुप्रस्थ) बनाए और प्रत्येक ट्रांसवर्सल (अनुप्रस्थ) में 9 बिंदु सम्मिलित थे जो इसे 10 भागों में विभाजित करते थे, जिसे 6 से गुणा करने पर 60 मिनट मिलते थे।[11] जबकि अब्द अल-मुनीम अल 'मिली (16वीं शताब्दी) ने उन सभी को एक ही दिशा में खींचा (यद्यपि उनके उपकरण में कम स्पष्टता है)।[12]
अन्य लेखक
खगोलीय और भौगोलिक उपकरणों में वृत्ताकार या अर्धवृत्ताकार अंगों पर कोणों की माप के लिए प्रयुक्त सीधे अनुप्रस्थ की विधि को कई लेखकों द्वारा इलाज किया गया था। प्रणालीकी स्पष्टता का अध्ययन करते हुए, उनमें से कुछ ने सीधे ट्रांसवर्सल (अनुप्रस्थ) के अतिरिक्त सर्कुलर ट्रांसवर्सल्स (अनुप्रस्थ) को नियोजित करने की सुविधा का संकेत दिया।[13]
यह भी देखें
- माइक्रोमीटर (डिवाइस)
- वर्नियर स्केल
संदर्भ
- ↑ Bernard R. Goldstein (6 December 2012). The Astronomy of Levi ben Gerson (1288–1344): A Critical Edition of Chapters 1–20 with Translation and Commentary. Springer Science & Business Media. pp. 164–. ISBN 978-1-4613-8569-1.
- ↑ Brian Lasater (2008). द ड्रीम ऑफ़ द वेस्ट, पं II. Lulu.com. pp. 355–. ISBN 978-1-4303-1382-3.
- ↑ Thomas Digges (1573). Alae seu scalae mathematicae, quibus visibilium remotissima coelorum theatra conscendi, & planetarum omnium itinera nouis & inauditis methodis explorari: ... Thoma Diggeseo, ... authore. pp. 86–.
- ↑ Joseph Needham (1959). Science and Civilisation in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press. pp. 296–. ISBN 978-0-521-05801-8.
- ↑ Jean Baptiste Joseph Delambre (1819). Histoire de l'astronomie du moyen age; par m. Delambre, chevalier de Saint-Michel et de la Legion-d'honneur . mme ve Courcier, imprimeur-libraire pour les sciences. pp. 372–.
- ↑ Aimé Laussedat (1898). Recherches sur les instruments: Aperçu historique sur les instruments et les méthodes. La topographie dans tous les temps. Gauthier-Villars.
- ↑ Maurice Daumas (1953). Les Instruments scientifiques aux XVIIe et XVIIIe siècles. Presses Universitaires de France.
- ↑ A.D. Morrison-Low (2 March 2017). औद्योगिक क्रांति में वैज्ञानिक उपकरण बनाना. Taylor & Francis. pp. 61–. ISBN 978-1-351-92074-2.
- ↑ 9.0 9.1 Tycho Brahe (1946). Tycho Brahe's description of his instruments and scientific work: as given in Astronomiae instauratae mechanica (Wandesburgi 1598). I Kommission hos E. Munksgaard.
- ↑ John Louis Emil Dreyer (13 February 2014). टाइको ब्राहे. Cambridge University Press. pp. 58–. ISBN 978-1-108-06871-0.
- ↑ Tycho Brahe (1602). Tychonis Brahe-Astronomiæ instauratæ mechanica. Noribergae [Nürnberg]: Levinum Hvlsivm.
- ↑ इस्तांबुल वेधशाला के उपकरण (1977). इस्तांबुल वेधशाला के उपकरण. p. 108.
- ↑ Allain Manesson-Mallet (1702). La Geometrie pratique: Tome second. Contenant la trigoniometrie, ou la mesure des distances par les instrumens geometriques ... chez Anisson directeur de l'Imprimerie Royale. pp. 32–.
ग्रन्थसूची
- Daumas, Maurice, Scientific Instruments of the Seventeenth and Eighteenth Centuries and Their Makers, Portman Books, London 1989 ISBN 978-0-7134-0727-3