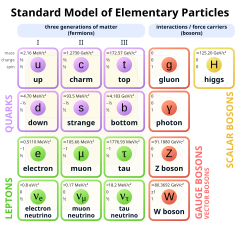
मानक मॉडल का गणितीय सूत्रीकरण

कण भौतिकी का मानक मॉडल। आरेख मानक मॉडल (हिग्स बॉसन, क्वार्क और लेपटोन की तीन पीढ़ी (कण भौतिकी), और गेज बोसॉन) के प्राथमिक कण को दिखाता है, जिसमें उनके नाम, द्रव्यमान, स्पिन, आवेश, चिरैलिटी और शक्त, और विद्युत चुम्बकीय बल के साथ अन्तःक्रिया सम्मिलित होती है। यह इलेक्ट्रोवीक समरूपता तोड़ने में हिग्स बोसोन की महत्वपूर्ण भूमिका को भी प्रदर्शित करता है, और दिखाता है कि विभिन्न कणों के गुण (उच्च-ऊर्जा) सममिति चरण (शीर्ष) और (कम-ऊर्जा) विघटित-समरूपता चरण (नीचे) में कैसे भिन्न होते हैं।

यह लेख कण भौतिकी के मानक मॉडल के गणित का वर्णन करता है, एक गेज सिद्धांत क्वांटम क्षेत्र सिद्धांत जिसमें क्षेत्र एकात्मक समूह $SU (3) \times SU(2) \times U(1)$ की आंतरिक समरूपता सम्मिलित होती है। सिद्धांत को सामान्यतः कणों के मूल समूह - लेप्टान, क्वार्क, गेज बोसॉन और हिग्स बोसोन का वर्णन करने के रूप में देखा जाता है।

मानक मॉडल पुनर्सामान्यीकरण योग्य और गणितीय रूप से आत्मनिर्भर होता है,^[1] यद्यपि प्रायोगिक भविष्यवाणियाँ प्रदान करने में बड़ी और निरंतर सफलताएँ मिलने के पश्चात् भी यह कुछ भौतिकी को मानक मॉडल से पृथक छोड़ देता है।^[2] विशेष रूप से, यद्यपि विशेष सापेक्षता के भौतिकी को सम्मिलित किया गया है, सामान्य सापेक्षता को सम्मिलित नहीं किया गया है, और मानक मॉडल उन ऊर्जाओं या दूरी पर विफल हो जाएगा जहां गुरुत्वाकर्षण उभरने की आशा होती है। इसलिए, आधुनिक क्षेत्र सिद्धांत संदर्भ में, इसे एक प्रभावी क्षेत्र सिद्धांत के रूप में देखा जाता है।

क्वांटम क्षेत्र सिद्धांत

अशक्त आइसोस्पिन का पैटर्न

T 3

, अशक्त अतिआवेश

Y W

, और सभी ज्ञात प्राथमिक कणों का रंग प्रभार, विद्युत आवेश दिखाने के लिए अशक्त मिश्रण कोण द्वारा घुमाया गया

Q

, मोटे तौर पर ऊर्ध्वाधर के साथ होता है। उदासीन हिग्स क्षेत्र (ग्रे वर्ग) विद्युत अशक्त समरूपता को तोड़ता है और अन्य कणों के साथ अन्तःक्रिया करके उन्हें द्रव्यमान देता है।

मानक मॉडल एक क्वांटम क्षेत्र सिद्धांत होता है, जिसका अर्थ है कि इसकी मूलभूत वस्तुएं क्वांटम क्षेत्र में होती हैं जिन्हें स्पेससमय में सभी बिंदुओं पर परिभाषित किया जाता है। क्यूएफटी कणों को उनके अंतर्निहित क्वांटम क्षेत्र (भौतिकी) की उत्तेजित अवस्था (जिसे क्वांटम भी कहा जाता है) के रूप में जाना जाता है, जो कणों की तुलना में अधिक मौलिक होते हैं। ये क्षेत्र इस प्रकार हैं

फरमिओन्स क्षेत्र, $ψ$ , जो पदार्थ के कणों का कारण बनता है;
इलेक्ट्रोवीक बोसोन क्षेत्र $W_{1},W_{2},W_{3}$ , और $B$ होते है;
ग्लूऑन क्षेत्र, $G a$ ; और
हिग्स बोसोन, $φ$ .

ये मौलिक क्षेत्रों के अतिरिक्त क्वांटम होता हैं, इसका गणितीय परिणाम यह है कि वे प्रचालक-मूल्यवान होता हैं। विशेष रूप से, क्षेत्र के मान सामान्यतः परिवर्तित नहीं होते हैं। प्रचालकों के रूप में, वे क्वांटम अवस्था (केट सदिश) पर कार्य करते हैं।

क्षेत्रों की वैकल्पिक प्रस्तुतियाँ

जैसा कि क्वांटम सिद्धांत में साधारण होता है, वस्तुओं को देखने की एक से अधिक विधियाँ होती है। पहले तो ऊपर दिए गए मूलभूत क्षेत्र ऊपर दिए गए चार्ट में मौलिक कणों के साथ पूर्ण रूप से समरूप नही होते है, परन्तु कई वैकल्पिक प्रस्तुतियाँ होती हैं, जो विशेष संदर्भों में, ऊपर दिए गए चार्ट की तुलना में अधिक उपयुक्त हो सकती हैं।

फर्मिअन्स

एक फर्मियन क्षेत्र $ψ$ होने के अतिरिक्त, इसे प्रत्येक प्रकार के कण के लिए भिन्न-भिन्न घटकों में विभाजित किया जा सकता है। यह क्वांटम क्षेत्र सिद्धांत के ऐतिहासिक विकास को प्रतिबिंबित करता है क्योंकि इलेक्ट्रॉन घटक $ψ e$ (इलेक्ट्रॉन और उसके प्रतिकण पोजीट्रान का वर्णन करना) क्वांटम विद्युतगतिकी का मूल $ψ$ क्षेत्र होता है, जिसे पश्चात् में क्रमशः म्यूऑन और टाऊन के लिए $ψ μ$ और $ψ τ$ क्षेत्र (और उनके प्रतिकण) को सम्मिलित किया गया था। इलेक्ट्रोवीक सिद्धांत $\psi _{\nu _{\mathrm {e} }},\psi _{\nu _{\mu }}$ , और $\psi _{\nu _{\tau }}$ संगत न्युट्रीनो के लिए जोड़ा जाता है। क्वार्क और भी घटक जोड़ते हैं। इलेक्ट्रॉन और अन्य लेप्टान घटकों के प्रकार से चार-स्पिनर होने के लिए, फ्लेवर और रंग के प्रत्येक संयोजन के लिए एक क्वार्क घटक होना चाहिए, जिससे कुल 24 हो जाए (आवेशित लेप्टान के लिए 3, न्यूट्रिनो के लिए 3, और 2·3·3 = 18 क्वार्क के लिए)। इनमें से प्रत्येक फर्मियन क्षेत्र के लिए कुल 96 समष्टि-मूल्यवान घटकों के लिए चार घटक वाला बिस्पिनोर होता है।

एक महत्वपूर्ण परिभाषा डिराक सहायक फर्मियन क्षेत्र ${\bar {\psi }}$ होता है, जिसे $\psi ^{\dagger }\gamma ^{0}$ द्वारा परिभाषित किया जाता है, जहाँ $\dagger$ , $ψ$ के हर्मिटियन जोड़ को प्रदर्शित करता है, और $γ 0$ शून्यवाँ गामा आव्यूह होता है। यदि $ψ$ को $n \times 1$ आव्यूह के रूप में माना जाता है तो ${\bar {\psi }}$ को $1 \times n$ आव्यूह के रूप में सोचा जाना चाहिए।

एक चिरल सिद्धांत

$ψ$ का एक स्वक्रियाविधि अपघटन चिरैलिटी घटकों में होता है:

"Left" chirality: $\psi ^{\rm {L}}={\frac {1}{2}}(1-\gamma _{5})\psi$
"Right" chirality: $\psi ^{\rm {R}}={\frac {1}{2}}(1+\gamma _{5})\psi$

जहाँ $\gamma _{5}$ पांचवां गामा आव्यूह होता है। मानक मॉडल में यह बहुत महत्वपूर्ण होता है क्योंकि बाएं और दाएं चिरैलिटी घटकों को गेज पारस्परिक क्रिया द्वारा भिन्न-भिन्न व्यवहार किया जाता है।

विशेष रूप से, अशक्त आइसोस्पिन SU(2) परिवर्तनों के अनुसार बाएं हाथ के कण अशक्त आइसोस्पिन दोहरे होते हैं, जबकि दाएं हाथ के कण एकल होते हैं - अर्थात् $ψ R$ का अशक्त आइसोस्पिन शून्य होता है। अधिक सरल पदों में कहें तो अशक्त अंतःक्रिया घूम सकती है, उदाहरण के लिए एक बाएं हाथ के इलेक्ट्रॉन को बाएं हाथ के न्यूट्रिनो में ( $W -$ के उत्सर्जन के साथ), परन्तु समान दाएँ हाथ के कणों के साथ ऐसा नहीं किया जा सकता है। एक ओर, दाएं हाथ के न्यूट्रिनो मूल रूप से मानक मॉडल में उपस्थित नहीं थे - परन्तु न्यूट्रिनो दोलन की अन्वेषण से पता चलता है कि न्यूट्रिनो में द्रव्यमान होना चाहिए, और चूंकि एक विशाल कण के प्रसार के समय चिरलिटी परिवर्तित हो सकती है, इसलिए वास्तविकता में दाएं हाथ के न्यूट्रिनो का अस्तित्व होना चाहिए। यद्यपि, यह अशक्त अंतःक्रिया की (प्रयोगात्मक रूप से सिद्ध) चिरल प्रकृति को नहीं परिवर्तित करता है।

आगे $U(1)$ , $\psi _{\mathrm {e} }^{\rm {L}}$ और $\psi _{\mathrm {e} }^{\rm {R}}$ पर अलग प्रकार से कार्य करता है (क्योंकि उनके पास भिन्न-भिन्न अशक्त अति आवेश होता हैं)।

द्रव्यमान और अंतःक्रिया ईजेनस्थिति

इस प्रकार, उदाहरण के लिए, न्यूट्रिनो के द्रव्यमान और अंतःक्रिया ईजेनस्थिति के मध्य अंतर किया जा सकता है। पूर्व वह अवस्था है जो मुक्त स्थान में फैलती है, जबकि पश्चात् वाली वह भिन्न अवस्था होती है जो अंतःक्रिया में भाग लेती है। मूल कण कौन सा है? न्यूट्रिनो के लिए, अंतःक्रिया ईजेनस्थिति द्वारा "फ्लेवर" (
ν
_e,
ν
_μ, या
ν
_τ) को परिभाषित करना पारंपरिक होता है, जबकि क्वार्क के लिए हम द्रव्यमान अवस्था द्वारा फ्लेवर (ऊपर, नीचे, आदि) को परिभाषित करते हैं। हम क्वार्क के लिए सीकेएम आव्यूह, या न्यूट्रिनो के लिए पीएमएनएस आव्यूह का उपयोग करके इन अवस्थाों के मध्य परिवर्तन कर सकते हैं (दूसरी ओर आवेश किए गए लेप्टान द्रव्यमान और फ्लेवर दोनों ईजेनस्थिति में होते हैं)।

एक ओर, यदि इनमें से किसी भी आव्यूह के भीतर एक समष्टि चरण पद उपस्थित होता है, तो यह प्रत्यक्ष सीपी उल्लंघन को उत्पन्न करेगा, जो हमारे वर्तमान ब्रह्मांड में प्रतिपदार्थ पर पदार्थ के प्रभुत्व को समझा सकता है। यह सीकेएम आव्यूह के लिए सिद्ध हो चुका है, और पीएमएनएस आव्यूह के लिए अपेक्षित होता है।

धनात्मक और ऋणात्मक ऊर्जा

अंत में, क्वांटम क्षेत्र कभी-कभी धनात्मक और ऋणात्मक ऊर्जा भागों $ψ = ψ + + ψ -$ में विघटित हो जाते हैं। जब क्वांटम क्षेत्र सिद्धांत स्थापित किया जाता है तो यह इतना सामान्य नहीं होता है, परन्तु प्रायः क्षेत्र सिद्धांत को परिमाणित करने की प्रक्रिया में प्रमुखता से प्रदर्शित होता है।

बोसोन

वेनबर्ग कोण

θ W

, और युग्मन स्थिरांक g, g', और e के मध्य संबंध। टी डी ली की पुस्तक कण भौतिकी और क्षेत्र सिद्धांत का परिचय (1981) से अनुकूलित होता है।

हिग्स क्रियाविधि के कारण, इलेक्ट्रोवीक बोसोन क्षेत्र $W_{1},W_{2},W_{3}$ , और $B$ ऐसी अवस्थाएँ बनाने के लिए मिश्रण करें जो भौतिक रूप से देखने योग्य होता है। गेज अपरिवर्तनीयता को बनाए रखने के लिए, अंतर्निहित क्षेत्र द्रव्यमान रहित होना चाहिए, परन्तु अवलोकन योग्य अवस्था से इस प्रक्रिया में द्रव्यमान प्राप्त कर सकते हैं। ये अवस्था इस प्रकार हैं:

विशाल उदासीन (Z) बोसोन:

Z=\cos \theta _{\rm {W}}W_{3}-\sin \theta _{\rm {W}}B

द्रव्यमान रहित उदासीन बोसॉन:

A=\sin \theta _{\rm {W}}W_{3}+\cos \theta _{\rm {W}}B

बड़े मापदंडों पर आवेशित W और Z बोसॉन:

W^{\pm }={\frac {1}{\sqrt {2}}}\left(W_{1}\mp iW_{2}\right)

जहाँ

θ W

वेनबर्ग कोण होता है। वह

A

क्षेत्र फोटॉन होता है, जो मौलिक रूप से प्रसिद्ध विद्युत चुम्बकीय चार-क्षमता के समरूप होता है - अर्थात् विद्युत और चुंबकीय क्षेत्र। वह

Z

क्षेत्र वास्तव में फोटॉन द्वारा की जाने वाली प्रत्येक प्रक्रिया में योगदान देता है, परन्तु इसके बड़े द्रव्यमान के कारण, योगदान सामान्यतः नगण्य होता है।

विघ्नकारी क्यूएफटी और अंतःक्रिया चित्र

"कणों" और "बलों" के संदर्भ में मानक मॉडल का अधिकांश गुणात्मक विवरण मॉडल के विक्षुब्ध क्वांटम क्षेत्र सिद्धांत दृष्टिकोण से आता है। इसमें लैग्रेंजियन को इस प्रकार विघटित किया जाता है भिन्न-भिन्न मुक्त क्षेत्र और पारस्परिक क्रिया लैग्रेन्जियन में ${\mathcal {L}}={\mathcal {L}}_{0}+{\mathcal {L}}_{\mathrm {I} }$ के रूप में विघटित किया जाता है। मुक्त क्षेत्र अलगाव में कणों की देखभाल करते हैं, जबकि कई कणों से जुड़ी प्रक्रियाएं परस्पर क्रिया के माध्यम से उत्पन्न होती हैं। विचार यह है कि अवस्था सदिश मात्र तभी बदलना चाहिए जब कण परस्पर क्रिया करते हैं, जिसका अर्थ है कि एक मुक्त कण वह होता है जिसकी क्वांटम स्थिति स्थिर होती है। यह क्वांटम यांत्रिकी में अंतःक्रिया चित्र के समरूप होता है

अधिक सामान्य श्रोडिंगर चित्र में, समय के साथ मुक्त कणों की अवस्थाएँ भी परिवर्तित होती हैं: सामान्यतः चरण उस दर से परिवर्तित होती है जो उनकी ऊर्जा पर निर्भर करता है। वैकल्पिक हाइजेनबर्ग चित्र में, प्रचालकों (विशेष रूप से अवलोकन योग्य) को समय-निर्भर होने के मूल्य पर, स्थिति सदिश को स्थिर रखा जाता है। अंतःक्रिया चित्र दोनों के मध्य एक मध्यवर्ती का गठन करता है, जहां कुछ समय निर्भरता प्रचालकों (क्वांटम क्षेत्र) में और कुछ अवस्था सदिश में रखी जाती है। क्यूएफटी में, पहले को मॉडल का मुक्त क्षेत्र भाग कहा जाता है, और पश्चात् वाले को अंतःक्रिया भाग कहा जाता है। मुक्त क्षेत्र मॉडल को स्पष्ट रूप से हल किया जा सकता है, और फिर पूर्ण मॉडल के समाधानों को मुक्त क्षेत्र समाधानों की अस्तव्यस्तता के रूप में व्यक्त किया जा सकता है, उदाहरण के लिए डायसन श्रृंखला का उपयोग करना।

यह देखा जाना चाहिए कि मुक्त क्षेत्रों और अंतःक्रियाओं में अपघटन सैद्धांतिक रूप से इच्छानुसार होता है। उदाहरण के लिए, क्वांटम विद्युतगतिकी में क्यूईडी में पुनर्सामान्यीकरण मुक्त क्षेत्र इलेक्ट्रॉन के द्रव्यमान को एक भौतिक इलेक्ट्रॉन (विद्युत चुम्बकीय क्षेत्र के साथ) से समरूप करने के लिए संशोधित करता है, और ऐसा करने पर मुक्त क्षेत्र लैग्रेंजियन में एक पद जुड़ जाएगा जिसे प्रतिवाद द्वारा रद्द किया जाना चाहिए। अंतःक्रिया लैग्रेंजियन, जो फिर फेनमैन आरेखों में दो-पंक्ति शीर्षके रूप में दिखाई देता है। यह भी माना जाता है कि हिग्स क्षेत्र कणों को अपरिवर्तनीय द्रव्यमान देता है: अंतःक्रिया पद का वह भाग जो हिग्स क्षेत्र के गैर-शून्य निर्वात अपेक्षा मूल्य के समरूप होता है, अंतःक्रिया से मुक्त क्षेत्र लैग्रेंजियन में ले जाया जाता है, जहां यह सम्पूर्ण रूप सें एक जैसा दिखता है सामूहिक पद का हिग्स क्षेत्र से कोई सम्बन्ध नहीं होता है।

मुक्त क्षेत्र

सामान्य मुक्त/पारस्परिक क्रिया अपघटन के अनुसार, जो कम ऊर्जा के लिए उपयुक्त होता है, मुक्त क्षेत्र निम्नलिखित समीकरणों का पालन करते हैं:

फर्मियन क्षेत्र $ψ$ डिराक समीकरण को संतुष्ट करता है; प्रत्येक $f$ प्रकार के फर्मियन के लिए $(i\hbar \gamma ^{\mu }\partial _{\mu }-m_{\rm {f}}c)\psi _{\rm {f}}=0$ करता है।
फोटॉन क्षेत्र $A$ तरंग समीकरण $\partial _{\mu }\partial ^{\mu }A^{\nu }=0$ को संतुष्ट करता है।
हिग्स क्षेत्र $φ$ क्लेन-गॉर्डन समीकरण को संतुष्ट करता है।
अशक्त अंतःक्रिया क्षेत्र $Z, W \pm$ प्रोका समीकरण को संतुष्ट करता है।

इन समीकरणों को सम्पूर्ण रूप से हल किया जा सकता है। ऐसा सामान्यतः पहले समाधानों पर विचार करके किया जाता है जो प्रत्येक स्थानिक अक्ष के साथ कुछ अवधि $L$ के साथ आवधिक होते हैं; पश्चात् में सीमा लेते हुए: $L \to \infty$ इस आवधिकता प्रतिबंध को हटा देगा।

आवधिक स्थिति में, एक क्षेत्र के लिए समाधान $F$ (उपरोक्त में से कोई भी) फॉर्म की फूरियर श्रृंखला के रूप में व्यक्त किया जा सकता है

F(x)=\beta \sum _{\mathbf {p} }\sum _{r}E_{\mathbf {p} }^{-{\frac {1}{2}}}\left(a_{r}(\mathbf {p} )u_{r}(\mathbf {p} )e^{-{\frac {ipx}{\hbar }}}+b_{r}^{\dagger }(\mathbf {p} )v_{r}(\mathbf {p} )e^{\frac {ipx}{\hbar }}\right)

जहाँ:

$β$ एक सामान्यीकरण कारक होता है; फर्मियन क्षेत्र $\psi _{\rm {f}}$ के लिए ${\textstyle {\sqrt {m_{\rm {f}}c^{2}/V}}}$ होता है, जहाँ $V=L^{3}$ मौलिक कक्ष का आयतन माना जाता है; फोटॉन क्षेत्र $A μ$ के लिए $\hbar c/{\sqrt {2V}}$ होता है।
$p$ से अवधि का योग सभी संवेगों पर है जो अवधि $L$ , अर्थात्, सभी सदिशों पर ${\frac {2\pi \hbar }{L}}(n_{1},n_{2},n_{3})$ होता है जहाँ $n_{1},n_{2},n_{3}$ पूर्णांक होता हैं।
$r$ से अधिक का योग क्षेत्र के लिए विशिष्ट स्वक्रियाविधिता की अन्य डिग्री को सम्मिलित करता है, जैसे ध्रुवीकरण या स्पिन; यह सामान्यतः $1$ को $2$ या से $1$ को $3$ के योग के रूप में निकलता है।
$E p$ क्षेत्र के संवेग $p$ के लिए सापेक्ष ऊर्जा होती है, जब शेष द्रव्यमान $m$ हो तो ${\textstyle ={\sqrt {m^{2}c^{4}+c^{2}\mathbf {p} ^{2}}}}$ होता है।
$a r (p)$ और $b_{r}^{\dagger }(\mathbf {p} )$ संवेग $p$ के क्रमशः ए-कणों और बी-कणों के लिए क्रमशः सृजन और विनाश संचालक होता हैं; बी-कण ए-कणों के प्रतिकण होते हैं। विभिन्न क्षेत्रों में भिन्न-भिन्न ए- और बी-कण होते हैं। कुछ क्षेत्रों के लिए, $a$ और $b$ समान होते हैं।
$u r (p)$ और $v r (p)$ गैर-संचालक होता हैं जो क्षेत्र के सदिश या स्पिनर पक्ष (जहां प्रासंगिक हो) को ले जाते हैं।
$p=(E_{\mathbf {p} }/c,\mathbf {p} )$ संवेग $p$ वाले एक क्वांटम के लिए चार-संवेग होता है। $px=p_{\mu }x^{\mu }$ चार-सदिशों के आंतरिक उत्पाद को प्रदर्शित करता है।

सीमा $L \to \infty$ में, योग $β$ के अंदर छिपे $V$ की सहायता एक अभिन्न अंग में परिवर्तित हो जाता है। $β$ का संख्यात्मक मान $u_{r}(\mathbf {p} )$ और $v_{r}(\mathbf {p} )$ इसके लिए चुने गए सामान्यीकरण पर भी निर्भर करता है।

विधिी रूप से, $a_{r}^{\dagger }(\mathbf {p} )$ केट सदिश के आंतरिक उत्पाद स्थान में संचालक $a r (p)$ का हर्मिटियन सहायक होता है। निर्माण और विनाश संचालकों के रूप में $a_{r}^{\dagger }(\mathbf {p} )$ और $a r (p)$ की पहचान अवस्था के लिए संरक्षित मात्राओं की तुलना करने से पहले और पश्चात् में होती हैं, जब इनमें से किसी एक ने इस पर कार्य किया हो। $a_{r}^{\dagger }(\mathbf {p} )$ उदाहरण के लिए एक कण को जोड़ते हुए देखा जा सकता है, क्योंकि यह ए-कण संख्या संचालक के आइजेनमान्य में $1$ जोड़ देगा, और उस कण की गति $p$ होनी चाहिए चूंकि सदिश-मूल्यवान संवेग संचालक का आइगेनमान्य बढ़ जाता है। इन व्युत्पत्तियों के लिए, क्वांटम क्षेत्र के संदर्भ में प्रचालकों के लिए अभिव्यक्तियों से प्रारम्भ किया जाता है। वह प्रचालकों के साथ $\dagger$ सृजन संचालक होता हैं और विनाश संचालक के बिना एक फलन होता है, जो उनके लिए निर्धारित रूपान्तरण संबंधों के संकेत द्वारा लगाया जाता है।

अस्तव्यस्त क्वांटम क्षेत्र सिद्धांत में गणना के निर्माण में एक महत्वपूर्ण चरण "संचालक" कारकों $a$ और $b$ उनके संबंधित सदिश या स्पिनर कारकों $u$ और $v$ को पृथक् करता है। फेनमैन ग्राफ के शीर्ष इस प्रकार से आते हैं की $u$ और $v$ पारस्परिक क्रिया में विभिन्न कारकों से लैग्रेंजियन एक साथ स्थापित होते हैं, जबकि सीमायें उस प्रकार से आती हैं की डायसन श्रृंखला में पदों को सामान्य रूप में रखने के लिए as और bs को चारों ओर ले जाती है।

अंतःक्रिया के उद्देश्य और पथ अभिन्न दृष्टिकोण

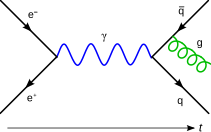
लैग्रेन्जियन को पथ अभिन्न सूत्रीकरण क्वांटम क्षेत्र सिद्धांत का उपयोग करके सृजन और विनाश प्रचालकों (कैनोनिकल औपचारिकता) का उपयोग किए बिना भी प्राप्त किया जा सकता है, जो डिराक के पहले के काम पर फेनमैन बिल्डिंग द्वारा अग्रणी होता है। फेनमैन आरेख अंतःक्रियात्मक पदों का सचित्र प्रतिनिधित्व होता हैं। फेनमैन आरेख पर लेख में वास्तव में एक त्वरित व्युत्पत्ति प्रस्तुत की गई है।

लैग्रेंजियन औपचारिकता

अब हम मानक मॉडल लैग्रेंजियन घनत्व में दिखाई देने वाले उपरोक्त मुक्त और पारस्परिक क्रिया पदों के बारे में कुछ और विवरण दे सकते है।^[3] ऐसा कोई भी पद गेज और संदर्भ-फ़्रेम दोनों अपरिवर्तनीय होना चाहिए, अन्यथा भौतिकी के नियम किसी पर्यवेक्षक की इच्छानुसार विकल्प या फ़्रेम पर निर्भर होंगे। इसलिए, वैश्विक समरूपता पोंकारे समरूपता, जिसमें अनुवादात्मक समरूपता, घूर्णी समरूपता और विशेष सापेक्षता के सिद्धांत के केंद्र में जड़त्वीय संदर्भ फ्रेम अपरिवर्तनीयता सम्मिलित होती है, जिसको प्रयुक्त किया जाना चाहिए। स्थानीय समरूपता $SU(3) \times SU(2) \times U(1)$ गेज समरूपता आंतरिक समरूपता होती है। जैसा कि हम देखेंगे, कुछ उपयुक्त संबंधों को परिभाषित करने के पश्चात्, गेज समरूपता के तीन कारक मिलकर तीन मूलभूत अंतःक्रियाओं को निर्मित करते हैं।

गतिज पद

एक मुक्त कण को एक द्रव्यमान पद और एक गतिज पद द्वारा प्रदर्शित किया जा सकता है जो क्षेत्रों की गति से संबंधित होता है।

फर्मिअन क्षेत्र

डिराक फर्मियन के लिए गतिज पद इस प्रकार है

i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi

जहां लेख में पहले से टिप्पणी दी गई हैं।

ψ

मानक मॉडल में किसी भी, या सभी, डिराक फ़र्मियन का प्रतिनिधित्व कर सकता है। सामान्यतः, जैसा कि नीचे दिया गया है, इस पद को युग्म (एक समग्र "गतिशील" पद बनाते हुए) के भीतर सम्मिलित किया गया है।

गेज क्षेत्र

स्पिन-1 क्षेत्र के लिए, पहले क्षेत्र स्ट्रेंथ टेंसर को परिभाषित करें

F_{\mu \nu }^{a}=\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}+gf^{abc}A_{\mu }^{b}A_{\nu }^{c}

किसी दिए गए गेज क्षेत्र के लिए (यहां हम उपयोग करते हैं

A

), गेज युग्मन स्थिरांक

g

के साथ। मात्रा

f abc

दिक्परिवर्तक द्वारा परिभाषित विशेष गेज समूह की संरचना स्थिरांक होता है

[t_{a},t_{b}]=if^{abc}t_{c},

जहाँ

t i

समूह के उत्पादक होता है। एबेलियन(कम्यूटेटिव) समूह में (जैसे कि

U(1)

जिसकाहम यहां उपयोग करते हैं) संरचना स्थिरांक लुप्त हो जाते हैं, क्योंकि सभी उत्पादक

t a

एक दूसरे के साथ आवागमन करते हैं। निस्संदेह, यह सामान्य रूप से स्थिति नहीं होती है - मानक मॉडल में गैर-एबेलियन

SU(2)

और

SU(3)

समूह (ऐसे समूह यांग-मिल्स सिद्धांत कहलाते हैं|यांग-मिल्स गेज सिद्धांत) को सम्मिलित करता है।

हमें प्रत्येक उपसमूह के अनुरूप तीन गेज क्षेत्र $SU(3) \times SU(2) \times U(1)$ प्रस्तुत करने की आवश्यकता होती है।

ग्लूऑन क्षेत्र टेंसर को $G_{\mu \nu }^{a}$ द्वारा निरूपित किया जाएगा, जहां सूचकांक $a$ के तत्वों को अंकित करता है रंग विशेष एकात्मक समूह का प्रतिनिधित्व SU(3) के $8$ प्रतिनिधित्व के तत्वों को अंकित करता है। दृढ़ युग्मन स्थिरांक को पारंपरिक रूप से $g s$ (या मात्र $g$ जहां कोई अस्पष्टता नहीं है)अंकित किया जाता है। मानक मॉडल के इस भाग की अन्वेषण के लिए किए गए अवलोकनों पर क्वांटम क्रोमोडायनामिक्स के लेख में चर्चा की गई है।
संकेतन $W_{\mu \nu }^{a}$ का उपयोग $SU(2)$ के गेज क्षेत्र टेंसर के लिए किया जाएगा जहाँ $a$ इस समूह के $3$ उत्पादक पर चलता है। युग्मन को $g w$ या फिर बस $g$ निरूपित किया जा सकता है। गेज क्षेत्र को $W_{\mu }^{a}$ द्वारा प्रदर्शित किया जाता है।
अशक्त अतिआवेश के $U(1)$ के लिए गेज क्षेत्र टेंसर को $B μν$ , द्वारा युग्मन $g'$ , और गेज क्षेत्र को $B μ$ .द्वारा प्रदर्शित किया जाएगा।

गतिज पद को अब इस प्रकार लिखा जा सकता है

{\mathcal {L}}_{\rm {kin}}=-{1 \over 4}B_{\mu \nu }B^{\mu \nu }-{1 \over 2}\mathrm {tr} W_{\mu \nu }W^{\mu \nu }-{1 \over 2}\mathrm {tr} G_{\mu \nu }G^{\mu \nu }

जहां पर चिन्ह क्रमशः

W

और

G

में छिपे

SU(2)

और

SU(3)

सूचकांक पर होते हैं । दो-सूचकांक ऑब्जेक्ट

W

और

G

सदिश क्षेत्र से प्राप्त क्षेत्र उर्जा होती है। दो अतिरिक्त छिपे हुए पैरामीटर: थीटा कोण

SU(2)

और

SU(3)

थीटा कोण भी होते है।

युग्मन उद्देश्य

आगामी चरण गेज क्षेत्र को फ़र्मियन से जोड़ना है, जिससे परस्पर क्रिया की अनुमति मिलती है।

इलेक्ट्रोवीक क्षेत्र

इलेक्ट्रोवीक क्षेत्र समरूपता समूह $U(1) \times SU(2) L$ के साथ अन्तःक्रिया करता है, जहां सबस्क्रिप्ट Lमात्र बाएं हाथ के फर्मियन के लिए युग्मन को इंगित करता है।

{\mathcal {L}}_{\mathrm {EW} }=\sum _{\psi }{\bar {\psi }}\gamma ^{\mu }\left(i\partial _{\mu }-g^{\prime }{1 \over 2}Y_{\mathrm {W} }B_{\mu }-g{1 \over 2}{\boldsymbol {\tau }}\mathbf {W} _{\mu }\right)\psi

जहाँ

B μ

U(1)

गेज क्षेत्र होता;

Y W

अशक्त अतिआवेश (

U(1)

समूहका उत्पादक) होता है;

W μ

तीन घटक

SU(2)

गेज क्षेत्र; और

τ

के घटक पॉल के आव्यूह (

SU(2)

समूह के अनंतिम उत्पादक) होते हैं जिनके आइगेनमान्य अशक्त आइसोस्पिन देते हैं। ध्यान दें कि अशक्त बलों के साथ एकीकरण प्राप्त करने के लिए हमें क्यूईडी से भिन्न एक नए

U(1)

को फिर से परिभाषित करना होगा। विद्युत आवेश

Q

, अशक्त आइसोस्पिन का तीसरा घटक

T 3

(यह भी कहा जाता है

T z, I 3

या

I z

भी कहा जाता है) और अशक्त अतिआवेश

Y W

से इस प्रकार संबंधित होता हैं

Q=T_{3}+{\tfrac {1}{2}}Y_{\rm {W}},

(या वैकल्पिक परिपाटी

Q = T 3 + Y W

द्वारा)। इस आलेख में प्रयुक्त प्रथम सम्मेलन, पहले के गेल-मान-निशिजिमा सूत्र के समान होता है। यह अतिआवेश को किसी दिए गए आइसोमल्टीप्लेट के औसत आवेश से दोगुना बनाता है।

फिर अशक्त आइसोस्पिन के लिए संरक्षित धारा को इस प्रकार परिभाषित किया जा सकता है

\mathbf {j} _{\mu }={1 \over 2}{\bar {\psi }}_{\rm {L}}\gamma _{\mu }{\boldsymbol {\tau }}\psi _{\rm {L}}

और अशक्त अतिआवेश के लिए

j_{\mu }^{Y}=2(j_{\mu }^{\rm {em}}-j_{\mu }^{3})~,

जहाँ

j_{\mu }^{\rm {em}}

विद्युत धारा और

j_{\mu }^{3}

तीसराअशक्तआइसोस्पिन धारा होती है। जैसा कि बोसॉन में समझाया गया है, ये धाराएँ भौतिक रूप से देखे गए बोसॉन बनाने के लिए मिश्रित होती हैं, जिससे युग्मन स्थिरांक के मध्य परीक्षण योग्य संबंध भी बनते हैं।

इसे सरल विधि से समझाने के लिए, हम लैग्रेंजियन से पदों को चुनकर इलेक्ट्रोवीक पारस्परिक क्रिया के प्रभाव को देख सकते हैं। हम देखते हैं कि SU(2) समरूपता इसमें निहित $ψ$ प्रत्येक (बाएं हाथ के) फर्मियन डबलेट पर कार्य करती है, उदाहरण के लिए

-{g \over 2}({\bar {\nu }}_{e}\;{\bar {e}})\tau ^{+}\gamma _{\mu }(W^{+})^{\mu }{\begin{pmatrix}{\nu _{e}}\\e\end{pmatrix}}=-{g \over 2}{\bar {\nu }}_{e}\gamma _{\mu }(W^{+})^{\mu }e

जहां कणों को बाएं हाथ का समझा जाता है, और जहां

\tau ^{+}\equiv {1 \over 2}(\tau ^{1}{+}i\tau ^{2})={\begin{pmatrix}0&1\\0&0\end{pmatrix}}

यह "अशक्त आइसोस्पिन स्थान में घूर्णन" या दूसरे शब्दों में,

W -

बोसोन के उत्सर्जन के माध्यम से

e L

और

ν eL

के मध्य एक परिवर्तन के अनुरूप एक पारस्परिक क्रिया होती है। दूसरी ओर

U(1)

समरूपता, विद्युत चुंबकत्व के समान होती है, परन्तु उदासीन

Z 0

के माध्यम से सभी अशक्त अतिआवेश फर्मियन (बाएं और दाएं दोनों) पर कार्य करती है, साथ ही फोटॉन के माध्यम से आवेशित फर्मियन पर भी कार्य करती है।

क्वांटम क्रोमोडायनामिक्स क्षेत्र

क्वांटम क्रोमोडायनामिक्स (क्यूसीडी) क्षेत्र $T a$ द्वारा उत्पन्न $SU(3)$ समरूपता के साथ क्वार्क और ग्लूऑन के मध्य पारस्परिक क्रिया को परिभाषित करता है। चूँकि लेप्टान ग्लूऑन के साथ परस्पर क्रिया नहीं करते हैं, इसलिए वे इस क्षेत्र से प्रभावित नहीं होते हैं। ग्लूऑन क्षेत्रों से जुड़े क्वार्कों का डिराक लैग्रेन्जियन द्वारा इस प्रकार दिया गया है

{\mathcal {L}}_{\mathrm {QCD} }=i{\overline {U}}\left(\partial _{\mu }-ig_{s}G_{\mu }^{a}T^{a}\right)\gamma ^{\mu }U+i{\overline {D}}\left(\partial _{\mu }-ig_{s}G_{\mu }^{a}T^{a}\right)\gamma ^{\mu }D.

जहाँ

U

और

D

ऊपर और नीचें-प्रकार के क्वार्क से जुड़े डायराक स्पिनर होते हैं, और अन्य संकेत चिन्ह पिछले अनुभाग से प्रवृत्त होते हैं।

द्रव्यमान पद और हिग्स क्रियाविधि

द्रव्यमान पद

डिराक लैग्रेंजियन (किसी भी फर्मियन $ψ$ के लिए) से उत्पन्न होने वाला द्रव्यमान पद $-m{\bar {\psi }}\psi$ होता है जो इलेक्ट्रोवीक समरूपता के अनुसार अपरिवर्तनीय नहीं होता है। $ψ$ इसे बाएँ और दाएँ हाथ के घटकों के संदर्भ में (वास्तविक गणना को छोड़कर) लिखकर देखा जा सकता है:

-m{\bar {\psi }}\psi =-m({\bar {\psi }}_{\rm {L}}\psi _{\rm {R}}+{\bar {\psi }}_{\rm {R}}\psi _{\rm {L}})

अर्थात्

{\bar {\psi }}_{\rm {L}}\psi _{\rm {L}}

और

{\bar {\psi }}_{\rm {R}}\psi _{\rm {R}}

के योगदान से उद्देश्य प्रकट नहीं होता है। हम देखते हैं कि द्रव्यमान-उत्पादक अंतःक्रिया कण चिरलिटी के निरंतर फ़्लिपिंग द्वारा प्राप्त की जाती है। स्पिन-आधे कणों के समान

SU(2)

प्रतिनिधित्व और समान और विपरीत अशक्त अतिआवेश साथ कोई दायां/बायां चिरैलिटी युग्म नहीं होता है , इसलिए यह मानते हुए कि ये गेज आवेश निर्वात में संरक्षित हैं, स्पिन-आधा कणों में से कोई भी कभी भी चिरलिटी को परिवर्तित नहीं कर सकता है, और इसे द्रव्यमान रहित रहना चाहिए। इसके अतिरिक्त, हम प्रयोगात्मक रूप से जानते हैं कि डब्ल्यू और जेड बोसॉन बड़े मापदंडों पर होताहैं, परन्तु बोसॉन द्रव्यमान पद में संयोजन सम्मिलित हैोता ह जैसे।

A μ A μ

, जो स्पष्ट रूप से गेज की विकल्प पर निर्भर करता है। इसलिए, कोई भी मानक मॉडल फर्मियन या बोसॉन द्रव्यमान से प्रारम्भ नहीं हो सकता है, परन्तु इसे किसी अन्य क्रियाविधि द्वारा प्राप्त करना होगा।

हिग्स क्रियाविधि

इन दोनों समस्याओं का समाधान हिग्स क्रियाविधि से आता है, जिसमें अदिश क्षेत्र सम्मिलित होता हैं (जिनकी संख्या हिग्स क्रियाविधि के स्पष्ट रूप पर निर्भर करती है) जो (संक्षिप्त रूप से संभव विवरण देने के लिए) बड़े मापदंडों पर बोसॉन द्वारा स्वक्रियाविधिता की डिग्री के रूप में अवशोषित होते हैं, और युकावा युग्मन के माध्यम से फर्मिऑन में कौन सा युग्म बड़े मापदंडों पर पदों के प्रकार को दिखता है।

मानक मॉडल में, हिग्स क्षेत्र समूह $SU(2) L$ का एक समष्टि अदिश क्षेत्र इस प्रकार है:

\phi ={\frac {1}{\sqrt {2}}}{\begin{pmatrix}\phi ^{+}\\\phi ^{0}\end{pmatrix}},

जहां सुपरस्क्रिप्ट

+

और

0

घटकों के विद्युत आवेश(

Q

) को इंगित करते है। दोनों घटकों का अशक्त अतिआवेश (

Y W

)

1

होता है।

लैग्रेन्जियन का हिग्स भाग इस प्रकार है

{\mathcal {L}}_{\rm {H}}=\left[\left(\partial _{\mu }-igW_{\mu }^{a}t^{a}-ig'Y_{\phi }B_{\mu }\right)\phi \right]^{2}+\mu ^{2}\phi ^{\dagger }\phi -\lambda (\phi ^{\dagger }\phi )^{2},

जहाँ

λ > 0

और

μ 2 > 0

होता, जिससे स्वतःस्फूर्त समरूपता टूटने की क्रियाविधि का उपयोग किया जा सके। यहां एक पैरामीटर होता है, सबसे पहले क्षमता के आकार के भीतर छिपा हुआ होता है, जो अत्यधिक महत्वपूर्ण होता है। एकीकरण गेज में कोई व्यक्ति

\phi ^{+}=0

कर सकता है और

\phi ^{0}

को वास्तविक बना सकता है। तब

\langle \phi ^{0}\rangle =v

हिग्स क्षेत्र का गैर-लुप्त होने वाला निर्वात प्रत्याशा मूल्य होता है।

v

द्रव्यमान की इकाइयाँ हैं, और यह मानक मॉडल में एकमात्र पैरामीटर होता है जो आयामहीन नहीं होता है। यह प्लैंक स्केल से भी बहुत छोटा है और हिग्स द्रव्यमान का लगभग दोगुना होता है, जो मानक मॉडल में अन्य सभी कणों के द्रव्यमान के लिए मापदंड निर्धारित करता है। मानक मॉडल में छोटे गैर-शून्य मान के लिए यह एकमात्र वास्तविक फाइन-ट्यूनिंग है। द्विघात पदों में

W μ

और

B μ

उत्पन्न होते हैं, जो W और Z बोसॉन को द्रव्यमान देते हैं:

{\begin{aligned}M_{\rm {W}}&={\tfrac {1}{2}}vg\\M_{\rm {Z}}&={\tfrac {1}{2}}v{\sqrt {g^{2}+{g'}^{2}}}\end{aligned}}

हिग्स बोसोन का द्रव्यमान स्वयं

{\textstyle M_{\rm {H}}={\sqrt {2\mu ^{2}}}\equiv {\sqrt {2\lambda v^{2}}}.}

द्वारा दिया गया है।

युकावा अंतःक्रिया

युकावा अंतःक्रिया का पद इस प्रकार हैं

{\mathcal {L}}_{\text{Yukawa}}=(Y_{u})_{mn}({\bar {q}}_{L})_{m}{\tilde {\varphi }}(u_{R})_{n}+(Y_{d})_{mn}({\bar {q}}_{L})_{m}\varphi (d_{R})_{n}+(Y_{e})_{mn}({\bar {L}}_{L})_{m}{\tilde {\varphi }}(e_{R})_{n}+\mathrm {h.c.}

जहाँ

Y_{u}

,

Y_{d}

, और

Y_{e}

3 \times 3

युकावा युग्म के आव्यूह, के साथ

mn

पीढ़ियों का युग्मन देने वाला पद

m

और

n

, और एच.सी.होता है इसका अर्थ पूर्ववर्ती पदों का हर्मिटियन संयुग्म होता है। क्षेत्र

q_{L}

और

L_{L}

बाएं हाथ के क्वार्क और लेप्टान युगल होते हैं। वैसे ही,

u_{R},d_{R}

और

e_{R}

दाएं हाथ के उपर-प्रकार क्वार्क, निचे-प्रकार क्वार्क और लेप्टान एकल होते हैं। अंत में

\varphi

हिग्स डबलट और

{\tilde {\varphi }}=i\tau _{2}\varphi ^{*}

होते है।

न्यूट्रिनो द्रव्यमान

जैसा कि पहले उल्लेख किया गया है, साक्ष्य से पता चलता है कि न्यूट्रिनो का द्रव्यमान होना चाहिए। परन्तु मानक मॉडल के भीतर, दाएं हाथ के न्यूट्रिनो उपस्थित नहीं होते हैं, इसलिए युकावा युग्मन के साथ भी न्यूट्रिनो द्रव्यमान रहित रहते हैं। एक स्पष्ट समाधान^[4] बस दाएं हाथ के न्यूट्रिनो $ν R$ को जोड़ना होता है, जिसके लिए युकावा क्षेत्र में एक नया डिराक द्रव्यमान पद जोड़ने की आवश्यकता होती है:

{\mathcal {L}}_{\nu }^{\text{Dir}}=(Y_{\nu })_{mn}({\bar {L}}_{L})_{m}\varphi (\nu _{R})_{n}+\mathrm {h.c.}

यद्यपि यह क्षेत्र एक बंध्‍य न्यूट्रिनो होना चाहिए, क्योंकि दाएँ हाथ से होने के कारण यह प्रयोगात्मक रूप से एक आइसोस्पिन एकल (

T 3 = 0

) से संबंधित होता है औरआवेश

Q = 0

होता है, जिसका अर्थ है

Y W = 0

(ऊपर देखें) होता है अर्थात् यह अशक्त पारस्परिक क्रिया में भी भाग नहीं लेता है। बंध्‍य न्यूट्रिनो के लिए प्रायोगिक साक्ष्य वर्तमान में अनिर्णायक होते हैं।^[5]

विचार करने की एक और संभावना यह है कि न्यूट्रिनो मेजराना समीकरण को संतुष्ट करता है, जो पहली बार में इसके शून्य विद्युत आवेश के कारण संभव लगता है। इस स्थिति में युकावा क्षेत्र में एक नया मेजराना द्रव्यमान पद युग्म जोड़ा जाता है:

{\mathcal {L}}_{\nu }^{\text{Maj}}=-{\frac {1}{2}}m\left({\overline {\nu }}^{C}\nu +{\overline {\nu }}\nu ^{C}\right)

जहाँ

C

एक आवेश संयुग्मित (अर्थात विरोधी) कण को प्रदर्शित करता है, और

\nu

पद लगातार सभी बाएं (या सभी दाएं) चिरैलिटी हैं (ध्यान दें कि एक प्रतिकण का बाएं-चिरालिटी प्रक्षेपण एक दाएं हाथ का क्षेत्र होता है; कभी-कभी उपयोग किए जाने वाले विभिन्न संकेत चिन्ह के कारण यहां सावधानी बरतनी चाहिए)। यहां हम अनिवार्य रूप से बाएं हाथ के न्यूट्रिनो और दाएं हाथ के प्रति-न्यूट्रिनो के मध्य फ़्लिप कर रहे हैं (यह भी संभव है परन्तु आवश्यक नहीं है कि न्यूट्रिनो अपने स्वयं के प्रतिकण हैं, इसलिए ये कण समान हैं)। यद्यपि, बाएं-चिरैलिटी न्यूट्रिनो के लिए, यह पद अशक्त अतिआवेश को 2 इकाइयों से बदल देता है - मानक हिग्स पारस्परिक क्रिया के साथ संभव नहीं है, अशक्त अतिआवेश = 2⁴ के साथ एक अतिरिक्त त्रिगुण को सम्मिलित करने के लिए हिग्स क्षेत्र को विस्तारित करने की आवश्यकता होती है^[4]-जबकि दाएं-चिरैलिटी न्यूट्रिनो के लिए, कोई हिग्स विस्तार आवश्यक नहीं होता है। बाएँ और दाएँ चिरैलिटी दोनों स्थितियों के लिए, मेजराना पद लेप्टन संख्या का उल्लंघन करते हैं, परन्तु संभवतः ऐसे उल्लंघनों का पता लगाने के लिए प्रयोगों की वर्तमान संवेदनशीलता से परे एक स्तर पर करते हैं।

डिराक और मेजराना दोनों द्रव्यमान पदों को एक ही सिद्धांत में सम्मिलित करना संभव होता है, जो (डिराक-द्रव्यमान-मात्र दृष्टिकोण के विपरीत) सही को जोड़कर, देखे गए न्यूट्रिनो द्रव्यमान की लघुता के लिए "प्राकृतिक" स्पष्टीकरण प्रदान कर सकता है। GUT मापदंडों के आसपास न्यूट्रिनो को अभी तक अज्ञात भौतिकी को दे दिया जाता है।^[6] (सीसॉ क्रियाविधि देखें)।

चूँकि किसी भी स्थिति में प्रयोगात्मक परिणामों को समझाने के लिए नए क्षेत्रों को निर्धारित किया जाना चाहिए, न्यूट्रिनो मानक मॉडल से परे भौतिकी की अन्वेषण के लिए एक स्पष्ट मार्ग होता है।

विस्तृत जानकारी

यह अनुभाग कुछ पक्ष और कुछ संदर्भ सामग्री पर अधिक विवरण प्रदान करता है। यहां स्पष्ट लैग्रेन्जियन पद भी उपलब्ध कराए गए हैं।

क्षेत्र सामग्री विस्तार से

मानक मॉडल में निम्नलिखित क्षेत्र होते हैं। ये लेप्टान और क्वार्क की एक पीढ़ी का वर्णन करते हैं, और इनमे तीन पीढ़ियाँ होती हैं, इसलिए प्रत्येक फर्मिओनिक क्षेत्र की तीन प्रतियां होती हैं। सीपीटी समरूपता द्वारा, विपरीत समता और आवेशों के साथ फ़र्मियन और प्रतिफ़र्मियन का एक समूह होता है। यदि बाएं हाथ का फर्मियन कुछ प्रतिनिधित्व को फैलाता है तो इसका प्रतिकण (दाएं हाथ का प्रतिफर्मियन) दोहरे प्रतिनिधित्व को फैलाता है^[7] (ध्यान दें कि ${\bar {\mathbf {2} }}={\mathbf {2} }$ SU(2) के लिए, क्योंकि यह सूडो-वास्तविक होता है)। स्तंभ प्रतिनिधित्व इंगित करता है कि गेज समूह के किस प्रतिनिधित्व सिद्धांत के अनुसार प्रत्येक क्षेत्र क्रम में परिवर्तित करता है (SU(3), SU(2), U(1))और U(1) समूह के लिए, अशक्त का मूल्य अतिआवेश सूचीबद्ध होता है। प्रत्येक पीढ़ी में दाएं हाथ के लेप्टान क्षेत्र घटकों की तुलना में बाएं हाथ के लेप्टान क्षेत्र घटकों की संख्या दोगुनी होती है, परन्तु बाएं हाथ के क्वार्क और दाएं हाथ के क्वार्क क्षेत्र घटकों की संख्या समान होती है।

मानक मॉडल की क्षेत्र सामग्री
Spin 1 – the gauge fields
Symbol	Associated charge	Group	Coupling	Representation^[8]
$B$	Weak hypercharge	$U(1) Y$	$g'$ or $g_{1}$	$(\mathbf {1} ,\mathbf {1} ,0)$
$W$	Weak isospin	$SU(2) L$	$g_{w}$ or $g_{2}$	$(\mathbf {1} ,\mathbf {3} ,0)$
$G$	colour	$SU(3) C$	$g_{s}$ or $g_{3}$	$(\mathbf {8} ,\mathbf {1} ,0)$
Spin 1⁄2 – the fermions
Symbol	Name	Baryon number	Lepton number	Representation
$q_{\rm {L}}$	Left-handed quark	$\textstyle {\frac {1}{3}}$	$0$	$(\mathbf {3} ,\mathbf {2} ,\textstyle {\frac {1}{3}})$
$u_{\rm {R}}$	Right-handed quark (up)	$\textstyle {\frac {1}{3}}$	$0$	$({\mathbf {3} },\mathbf {1} ,\textstyle {\frac {4}{3}})$
$d_{\rm {R}}$	Right-handed quark (down)	$\textstyle {\frac {1}{3}}$	$0$	$({\mathbf {3} },\mathbf {1} ,-\textstyle {\frac {2}{3}})$
$\ell _{\rm {L}}$	Left-handed lepton	$0$	$1$	$(\mathbf {1} ,\mathbf {2} ,-1)$
$\ell _{\rm {R}}$	Right-handed lepton	$0$	$1$	$(\mathbf {1} ,\mathbf {1} ,-2)$
Spin 0 – the scalar boson
Symbol	Name	Representation
$H$	Higgs boson	$(\mathbf {1} ,\mathbf {2} ,1)$

फर्मिअन सामग्री

यह निर्देशिका आंशिक रूप से कण डेटा समूह द्वारा एकत्र किए गए डेटा पर आधारित होती है।^[9]

मानक मॉडल में बाएँ हाथ के फर्मियन
Generation 1
Fermion (left-handed)	Symbol	Electric charge	Weak isospin	Weak hypercharge	Color charge ^{[lhf 1]}	Mass^{[lhf 2]}
Electron	$e -$	$-1$	$-{\tfrac {1}{2}}$	$-1$	$\mathbf {1}$	511 keV
Positron	$e +$	$+1$	$~\ 0$	$+2$	$\mathbf {1}$	511 keV
Electron neutrino	$ν e$	$~\ 0$	$+{\tfrac {1}{2}}$	$-1$	$\mathbf {1}$	< 0.28 eV^{[lhf 3]}^{[lhf 4]}
Electron antineutrino	$ν e$	$~\ 0$	$~\ 0$	$~\ 0$	$\mathbf {1}$	< 0.28 eV^{[lhf 3]}^{[lhf 4]}
Up quark	$u$	$+{\tfrac {2}{3}}$	$+{\tfrac {1}{2}}$	$+{\tfrac {1}{3}}$	$\mathbf {3}$	~ 3 MeV^{[lhf 5]}
Up antiquark	$u$	$-{\tfrac {2}{3}}$	$~\ 0$	$-{\tfrac {4}{3}}$	$\mathbf {\bar {3}}$	~ 3 MeV^{[lhf 5]}
Down quark	$d$	$-{\tfrac {1}{3}}$	$-{\tfrac {1}{2}}$	$+{\tfrac {1}{3}}$	$\mathbf {3}$	~ 6 MeV^{[lhf 5]}
Down antiquark	$d$	$+{\tfrac {1}{3}}$	$~\ 0$	$+{\tfrac {2}{3}}$	$\mathbf {\bar {3}}$	~ 6 MeV^{[lhf 5]}

Generation 2
Fermion (left-handed)	Symbol	Electric charge	Weak isospin	Weak hypercharge	Color charge ^{[lhf 1]}	Mass ^{[lhf 2]}
Muon	$μ -$	$-1$	$-{\tfrac {1}{2}}$	$-1$	$\mathbf {1}$	106 MeV
Antimuon	$μ +$	$+1$	$~\ 0$	$+2$	$\mathbf {1}$	106 MeV
Muon neutrino	$ν μ$	$~0$	$+{\tfrac {1}{2}}$	$-1$	$\mathbf {1}$	< 0.28 eV^{[lhf 3]}^{[lhf 4]}
Muon antineutrino	$ν μ$	$~\ 0$	$~\ 0$	$~\ 0$	$\mathbf {1}$	< 0.28 eV^{[lhf 3]}^{[lhf 4]}
Charm quark	$c$	$+{\tfrac {2}{3}}$	$+{\tfrac {1}{2}}$	$+{\tfrac {1}{3}}$	$\mathbf {3}$	~ 1.3 GeV
Charm antiquark	$c$	$-{\tfrac {2}{3}}$	$~\ 0$	$-{\tfrac {4}{3}}$	$\mathbf {\bar {3}}$	~ 1.3 GeV
Strange quark	$s$	$-{\tfrac {1}{3}}$	$-{\tfrac {1}{2}}$	$+{\tfrac {1}{3}}$	$\mathbf {3}$	~ 100 MeV
Strange antiquark	$s$	$+{\tfrac {1}{3}}$	$~\ 0$	$+{\tfrac {2}{3}}$	$\mathbf {\bar {3}}$	~ 100 MeV

Generation 3
Fermion (left-handed)	Symbol	Electric charge	Weak isospin	Weak hypercharge	Color charge ^{[lhf 1]}	Mass^{[lhf 2]}
Tau	$τ -$	$-1$	$-{\tfrac {1}{2}}$	$-1$	$\mathbf {1}$	1.78 GeV
Antitau	$τ +$	$+1$	$~\ 0$	$+2$	$\mathbf {1}$	1.78 GeV
Tau neutrino	$ν τ$	$~\ 0$	$+{\tfrac {1}{2}}$	$-1$	$\mathbf {1}$	< 0.28 eV^{[lhf 3]}^{[lhf 4]}
Tau antineutrino	$ν τ$	$~\ 0$	$~\ 0$	$~\ 0$	$\mathbf {1}$	< 0.28 eV^{[lhf 3]}^{[lhf 4]}
Top quark	$t$	$+{\tfrac {2}{3}}$	$+{\tfrac {1}{2}}$	$+{\tfrac {1}{3}}$	$\mathbf {3}$	171 GeV
Top antiquark	$t$	$-{\tfrac {2}{3}}$	$~\ 0$	$-{\tfrac {4}{3}}$	$\mathbf {\bar {3}}$	171 GeV
Bottom quark	$b$	$-{\tfrac {1}{3}}$	$-{\tfrac {1}{2}}$	$+{\tfrac {1}{3}}$	$\mathbf {3}$	~ 4.2 GeV
Bottom antiquark	$b$	$+{\tfrac {1}{3}}$	$~\ 0$	$+{\tfrac {2}{3}}$	$\mathbf {\bar {3}}$	~ 4.2 GeV

↑ ^1.0 ^1.1 ^1.2 These are not ordinary abelian charges, which can be added together, but are labels of group representations of Lie groups. ↑ ^2.0 ^2.1 ^2.2 Mass is really a coupling between a left-handed fermion and a right-handed fermion. For example, the mass of an electron is really a coupling between a left-handed electron and a right-handed electron, which is the antiparticle of a left-handed positron. Also neutrinos show large mixings in their mass coupling, so it's not accurate to talk about neutrino masses in the flavor basis or to suggest a left-handed electron antineutrino. ↑ ^3.0 ^3.1 ^3.2 ^3.3 ^3.4 ^3.5 The Standard Model assumes that neutrinos are massless. However, many contemporary experiments prove that neutrinos oscillate between their flavour states, which could not happen if all were massless. It is straightforward to extend the model to fit these data but there are many possibilities, so the mass eigenstates are still open. See neutrino mass. ↑ ^4.0 ^4.1 ^4.2 ^4.3 ^4.4 ^4.5 Yao, W.-M.; et al. (Particle Data Group) (2006). "Review of Particle Physics: Neutrino mass, mixing, and flavor change" (PDF). Journal of Physics G. 33 (1): 1. arXiv:astro-ph/0601168. Bibcode:2006JPhG...33....1Y. doi:10.1088/0954-3899/33/1/001. S2CID 117958297. ↑ ^5.0 ^5.1 ^5.2 ^5.3 The masses of baryons and hadrons and various cross-sections are the experimentally measured quantities. Since quarks can't be isolated because of QCD confinement, the quantity here is supposed to be the mass of the quark at the renormalization scale of the QCD scale.

मुक्त पैरामीटर

द्रव्यमान रहित न्यूट्रिनो के साथ सबसे सामान्य लैग्रेंजियन लिखने पर, ऐसा पाया जाता है कि गतिशीलता 19 मापदंडों पर निर्भर करती है, जिनके संख्यात्मक मान प्रयोग द्वारा स्थापित किए जाते हैं। विशाल न्यूट्रिनो के साथ मानक मॉडल के सीधे विस्तार के लिए कुल 26 मापदंडों के लिए 7 और मापदंडों (3 द्रव्यमान और 4 पीएमएनएस आव्यूह पैरामीटर) की आवश्यकता होती है।^[10] न्यूट्रिनो पैरामीटर मान अभी भी अनिश्चित होतेहैं। 19 निश्चित मापदंडों को यहां संक्षेप में प्रस्तुत किया गया है।

मानक मॉडल के पैरामीटर
Symbol	Description	Renormalization scheme (point)	Value	Experimental uncertainty
m_e	Electron mass		510.9989461 keV	±3.1 meV
m_μ	Muon mass		105.6583745 MeV	±2.4 eV
m_τ	Tau mass		1.77686 GeV	±0.12 MeV
m_u	Up quark mass	μ_MS = 2 GeV	2.16 MeV	+0.49 −0.26 MeV
m_d	Down quark mass	μ_MS = 2 GeV	4.67 MeV	+0.48 −0.17 MeV
m_s	Strange quark mass	μ_MS = 2 GeV	93.4 MeV	+8.6 −3.4 MeV
m_c	Charm quark mass	μ_MS = m_c	1.27 GeV	±0.02 GeV
m_b	Bottom quark mass	μ_MS = m_b	4.18 GeV	+0.03 −0.02 GeV
m_t	Top quark mass	On-shell scheme	172.69 GeV	±0.30 GeV
θ₁₂	CKM 12-mixing angle		13.1°
θ₂₃	CKM 23-mixing angle		2.4°
θ₁₃	CKM 13-mixing angle		0.2°
δ	CKM CP-violating Phase		0.995
g₁ or g'	U(1) gauge coupling	μ_MS = m_Z	0.357
g₂ or g	SU(2) gauge coupling	μ_MS = m_Z	0.652
g₃ or g_s	SU(3) gauge coupling	μ_MS = m_Z	1.221
θ_QCD	QCD vacuum angle		~0
v	Higgs vacuum expectation value		246.2196 GeV	±0.2 MeV
m_H	Higgs mass		125.18 GeV	±0.16 GeV

मुक्त मापदंडों का चुनाव कुछ मात्रा में इच्छानुसार होता है। उपरोक्त निर्देशिका में, गेज युग्म को मुफ़्त पैरामीटर के रूप में सूचीबद्ध किया गया है, इसलिए इस विकल्प के साथ वेनबर्ग कोण एक मुफ़्त पैरामीटर नहीं होता है - इसे इस प्रकार $\tan \theta _{\rm {W}}={\frac {g_{1}}{g_{2}}}$ परिभाषित किया गया है। इसी प्रकार, QED की सूक्ष्म संरचना स्थिरांक $\alpha ={\frac {1}{4\pi }}{\frac {(g_{1}g_{2})^{2}}{g_{1}^{2}+g_{2}^{2}}}$ होता है। फर्मियन द्रव्यमान के अतिरिक्त, आयाम रहित युकावा युग्म को मुक्त पैरामीटर के रूप में चयनित किया जा सकता है। उदाहरण के लिए, इलेक्ट्रॉन द्रव्यमान हिग्स क्षेत्र में इलेक्ट्रॉन के युकावा युग्मन पर निर्भर करता है, और इसका मान $m_{\rm {e}}={\frac {y_{\rm {e}}}{\sqrt {2}}}v$ होता है।हिग्स द्रव्यमान के अतिरिक्त, हिग्स स्व-युग्मन शक्ति $\lambda ={\frac {m_{\rm {H}}^{2}}{2v^{2}}}$ , जो आनुमानित 0.129 होती है, को एक मुक्त पैरामीटर के रूप में चयनित की जा सकती है। हिग्स निर्वात अपेक्षा मूल्य के अतिरिक्त, $\mu ^{2}$ हिग्स स्वतः-पारस्परिक क्रिया पद से सीधे पैरामीटर $\mu ^{2}\phi ^{\dagger }\phi -\lambda (\phi ^{\dagger }\phi )^{2}$ का चयन किया जा सकता है। इसका मान $\mu ^{2}=\lambda v^{2}={\frac {m_{\rm {H}}^{2}}{2}}$ , या आनुमानित $\mu =88.45$ GeV होता है।

निर्वात ऊर्जा का मान (या अधिक स्पष्ट रूप से, इस ऊर्जा की गणना करने के लिए उपयोग किया जाने वाला पुनर्सामान्यीकरण मापदंड) को एक अतिरिक्त मुक्त पैरामीटर के रूप में भी माना जा सकता है। पुनर्सामान्यीकरण मापदंडों को प्लैंक मापक से पहचाना जा सकता है या प्रेक्षित ब्रह्माण्ड संबंधी स्थिरांक से समरूप करने के लिए इसे ठीक किया जा सकता है। यद्यपि, दोनों विकल्प ब्रह्माण्ड संबंधी स्थिरांक समस्या होते हैं।^[11]

मानक मॉडल की अतिरिक्त समरूपताएँ

सैद्धांतिक दृष्टिकोण से, मानक मॉडल चार अतिरिक्त वैश्विक समरूपता प्रदर्शित करता है, जो इसके निर्माण के प्रारम्भ में नहीं बताई गई है, सामूहिक रूप से आकस्मिक समरूपता को प्रदर्शितकिया गया है, जो निरंतर U(1) वैश्विक समरूपता होती है। लैग्रेन्जियन अपरिवर्तनीय को वर्जित करने वाले परिवर्तन इस प्रकार हैं:

\psi _{\text{q}}(x)\to e^{i\alpha /3}\psi _{\text{q}}

E_{\rm {L}}\to e^{i\beta }E_{\rm {L}}{\text{ and }}(e_{\rm {R}})^{c}\to e^{i\beta }(e_{\rm {R}})^{c}

M_{\rm {L}}\to e^{i\beta }M_{\rm {L}}{\text{ and }}(\mu _{\rm {R}})^{c}\to e^{i\beta }(\mu _{\rm {R}})^{c}

T_{\rm {L}}\to e^{i\beta }T_{\rm {L}}{\text{ and }}(\tau _{\rm {R}})^{c}\to e^{i\beta }(\tau _{\rm {R}})^{c}

पहला परिवर्तन नियम आशुलिपि है जिसका अर्थ है कि सभी पीढ़ियों के लिए सभी क्वार्क क्षेत्रों को एक समान चरण द्वारा एक साथ घुमाया जाना चाहिए। क्षेत्र

M L, T L

और

(\mu _{\rm {R}})^{c},(\tau _{\rm {R}})^{c}

की दूसरी (मुऑन) और तीसरी (ताऊ) पीढ़ी के एनालॉग

E L

और

(e_{\rm {R}})^{c}

क्षेत्र होते है।

नोएथर के प्रमेय के अनुसार, उपरोक्त प्रत्येक समरूपता से संबंधित संरक्षण नियम है: बेरिऑन संख्या का संरक्षण,^[12] लेप्टान संख्या, लेप्टान संख्या, और लेप्टान संख्या। प्रत्येक क्वार्क को एक बेरिऑन संख्या ${\textstyle {\frac {1}{3}}}$ दी गई है, जबकि प्रत्येक प्रतिक्वार्क को एक बेरिऑन संख्या ${\textstyle -{\frac {1}{3}}}$ दी गई है। बेरिऑन संख्या के संरक्षण का अर्थ है कि क्वार्कों की संख्या घटाकर प्रतिक्वार्कों की संख्या एक स्थिरांक है। प्रायोगिक सीमा के भीतर, इस संरक्षण नियम का कोई उल्लंघन नहीं पाया गया है।

इसी प्रकार, प्रत्येक इलेक्ट्रॉन और उससे जुड़े न्यूट्रिनो को +1 का इलेक्ट्रॉन नंबर दिया जाता है, जबकि पॉज़िट्रॉन प्रति-इलेक्ट्रॉन और संबंधित प्रति-न्यूट्रिनो को -1 इलेक्ट्रॉन नंबर दिया जाता है। इसी प्रकार, म्यूऑन और उनके न्यूट्रिनो को +1 की म्यूऑन संख्या दी गई है और टाउ लेप्टान को +1 की ताउ लेप्टान संख्या दी गई है। मानक मॉडल भविष्यवाणी करता है कि इन तीन संख्याओं में से प्रत्येक को उसी प्रकार से भिन्न-भिन्न संरक्षित किया जाना चाहिए जिस प्रकार से बैरियन संख्या को संरक्षित किया जाता है। इन संख्याओं को सामूहिक रूप से लेप्टान परिवार संख्या (एलएफ) के रूप में जाना जाता है। (यह परिणाम मानक मॉडल में की गई धारणा पर निर्भर करता है कि न्यूट्रिनो द्रव्यमान रहित होता हैं। प्रयोगात्मक रूप से, न्यूट्रिनो दोलन प्रदर्शित करता हैं कि व्यक्तिगत इलेक्ट्रॉन, म्यूऑन और ताऊ संख्याएं संरक्षित नहीं होती हैं।)^[13]^[14]

ऊपर वर्णित आकस्मिक (परन्तु स्पष्ट) समरूपता के अतिरिक्त, मानक मॉडल कई कण भौतिकी और प्रतिनिधित्व सिद्धांत अनुमानित समरूपता प्रदर्शित करता है। ये "SU(2) संरक्षक समरूपता" और "SU(2) या SU(3) क्वार्क फ्लेवर समरूपता" होती है।

मानक मॉडल की समरूपता और संबंधित संरक्षण नियम
Symmetry	Lie group	Symmetry Type	Conservation law
Poincaré	Translations ⋊SO(3,1)	Global symmetry	Energy, Momentum, Angular momentum
Gauge	SU(3)×SU(2)×U(1)	Local symmetry	Color charge, Weak isospin, Electric charge, Weak hypercharge
Baryon phase	U(1)	Accidental Global symmetry	Baryon number
Electron phase	U(1)	Accidental Global symmetry	Electron number
Muon phase	U(1)	Accidental Global symmetry	Muon number
Tau phase	U(1)	Accidental Global symmetry	Tau number

U(1) समरूपता

लेप्टान के लिए, गेज समूह को $SU(2) l \times U(1) L \times U(1) R$ लिखा जा सकता है। दो U(1) कारकों को $U(1) Y \times U(1) l$ में जोड़ा जा सकता है जहां l लेप्टान संख्या होती है। लेप्टान संख्या की गेजिंग को प्रयोग द्वारा रद्द कर दिया जाता है, मात्र संभावित गेज समूह $SU(2) L \times U(1) Y$ को छोड़ दिया जाता है। क्वार्क क्षेत्र में एक समान तर्क इलेक्ट्रोवीक सिद्धांत के लिए भी समान परिणाम देता है।

आवेशित और उदासीन धारा युग्म और फर्मी सिद्धांत

आवेशित धाराएँ $j^{\mp }=j^{1}\pm ij^{2}$ होती हैं

j_{\mu }^{-}={\overline {U}}_{i\mathrm {L} }\gamma _{\mu }D_{i\mathrm {L} }+{\overline {\nu }}_{i\mathrm {L} }\gamma _{\mu }l_{i\mathrm {L} }.

ये आवेशित धाराएँ सम्पूर्ण रूप सें वही होती हैं जो बीटा क्षय के फर्मी सिद्धांत में लेख्यांकित हुई थीं। क्रिया में आवेश धारा का कुछ भाग सम्मिलित होता है

{\mathcal {L}}_{\rm {CC}}={\frac {g}{\sqrt {2}}}(j_{\mu }^{+}W^{-\mu }+j_{\mu }^{-}W^{+\mu }).

डब्ल्यू-बोसोन के द्रव्यमान से बहुत कम ऊर्जा के लिए, प्रभावी सिद्धांत फर्मी की अन्योन्यक्रिया की वर्तमान-वर्तमान संपर्क अंतःक्रिया बन जाता है,

2{\sqrt {2}}G_{\rm {F}}~~J_{\mu }^{+}J^{\mu ~~-}

.

यद्यपि, गेज अपरिवर्तनीयता के लिए अब घटक $W^{3}$ की आवश्यकता होती है गेज क्षेत्र को भी एक धारा से जोड़ा जाना चाहिए जो SU(2) के त्रिक में निहित होती है। यद्यपि, यह U(1) के साथ मिश्रित होता है, और उस क्षेत्र में एक और धारा की आवश्यकता होती है। आवेश को संरक्षित करने के लिए इन धाराओं को अनावेशित किया जाना चाहिए। अत: उदासीन धाराओं की भी आवश्यकता होती है,

j_{\mu }^{3}={\frac {1}{2}}\left({\overline {U}}_{i\mathrm {L} }\gamma _{\mu }U_{i\mathrm {L} }-{\overline {D}}_{i\mathrm {L} }\gamma _{\mu }D_{i\mathrm {L} }+{\overline {\nu }}_{i\mathrm {L} }\gamma _{\mu }\nu _{i\mathrm {L} }-{\overline {l}}_{i\mathrm {L} }\gamma _{\mu }l_{i\mathrm {L} }\right)

j_{\mu }^{\rm {em}}={\frac {2}{3}}{\overline {U}}_{i}\gamma _{\mu }U_{i}-{\frac {1}{3}}{\overline {D}}_{i}\gamma _{\mu }D_{i}-{\overline {l}}_{i}\gamma _{\mu }l_{i}.

तब लैग्रेन्जियन में उदासीन धारा का कुछ भाग इस प्रकार होता है

${\mathcal {L}}_{\rm {NC}}=ej_{\mu }^{\rm {em}}A^{\mu }+{\frac {g}{\cos \theta _{\rm {W}}}}(J_{\mu }^{3}-\sin ^{2}\theta _{\rm {W}}J_{\mu }^{\rm {em}})Z^{\mu }.$ मानक मॉडल से परे भौतिकी

Page 'Physics beyond the Standard Model' not found

यह भी देखें

कण भौतिकी के मानक मॉडल का अवलोकन
मौलिक अंतःक्रिया
गैर-अनुवांशिक मानक मॉडल
विवृत प्रश्न: सीपी उल्लंघन, न्यूट्रिनो, क्यूसीडी स्थति
मानक मॉडल से परे भौतिकी
दृढ़ अन्तःक्रिया
- फ्लेवर (कण भौतिकी)
- क्वांटम क्रोमोडायनामिक्स
- क्वार्क मॉडल
दृढ़ अन्तःक्रिया
- इलेक्ट्रोवीक अंतःक्रिया
- फर्मी की अन्तःक्रिया
वेनबर्ग कोण
क्वांटम यांत्रिकी में समरूपता
ए. ज़ी द्वारा संक्षेप में क्वांटम क्षेत्र सिद्धांत

संदर्भ और बाहरी लिंक

क्वांटम क्षेत्र सिद्धांत का परिचय, एम.ई. पेस्किन और डी.वी. द्वारा। श्रोएडर (हार्पर कॉलिन्स, 1995) ISBN 0-201-50397-2.
प्रारंभिक कण भौतिकी का गेज सिद्धांत, टी.पी. द्वारा। चेंग और एल.एफ. ली (ऑक्सफोर्ड यूनिवर्सिटी प्रेस, 1982) ISBN 0-19-851961-3.
स्पष्ट हिग्स शर्तों के साथ मानक मॉडल लैग्रेंजियन (टी.डी. गुटिरेज़, सीए 1999) (पीडीएफ, पोस्टस्क्रिप्ट, और लाटेक्स संस्करण)
फील्ड्स का क्वांटम सिद्धांत (खंड 2), एस. वेनबर्ग द्वारा (कैम्ब्रिज यूनिवर्सिटी प्रेस, 1996) ISBN 0-521-55002-5.
क्वांटम फील्ड थ्योरी संक्षेप में (दूसरा संस्करण), ए. ज़ी द्वारा (प्रिंसटन यूनिवर्सिटी प्रेस, 2010) ISBN 978-1-4008-3532-4.
आर. मान द्वारा कण भौतिकी और मानक मॉडल का एक परिचय (सीआरसी प्रेस, 2010) ISBN 978-1420082982
फिजिक्स फ्रॉम सिमिट्री जे. श्विटेनबर्ग द्वारा (स्प्रिंगर, 2015) ISBN 3319192000. विशेषकर पृष्ठ 86

श्रेणी:मानक मॉडल श्रेणी:इलेक्ट्रोवीक सिद्धांत

↑ In fact, there are mathematical issues regarding quantum field theories still under debate (see e.g. Landau pole), but the predictions extracted from the Standard Model by current methods are all self-consistent. For a further discussion see e.g. R. Mann, chapter 25.
↑ Overbye, Dennis (11 September 2023). "Don't Expect a 'Theory of Everything' to Explain It All - Not even the most advanced physics can reveal everything we want to know about the history and future of the cosmos, or about ourselves". The New York Times. Archived from the original on 11 September 2023. Retrieved 11 September 2023.
↑ Lindon, Jack (2020). एलएचसी पर एटलस डिटेक्टर का उपयोग करते हुए एक ऊर्जावान जेट और बड़े लापता अनुप्रस्थ गति के साथ घटनाओं में डार्क एनर्जी, डार्क मैटर और मानक मॉडल हस्ताक्षरों से परे जेनेरिक के कण कोलाइडर जांच (PhD). CERN.
↑ ^4.0 ^4.1 Raby, Stuart; Slansky, Richard. "न्यूट्रिनो द्रव्यमान - उन्हें मानक मॉडल में कैसे जोड़ें" (PDF). FAS Project on Government Secrecy. Retrieved 3 November 2023.
↑ "न्यूट्रिनो दोलन आज". t2k-experiment.org.
↑ "संग्रहीत प्रति" (PDF). Archived from the original (PDF) on 2014-02-26. Retrieved 2014-02-26.
↑ "2.3.1 Isospin and SU(2), Redux". math.ucr.edu. Retrieved 2020-08-09.
↑ McCabe, Gordon. (2007). The structure and interpretation of the standard model. Amsterdam: Elsevier. pp. 160–161. ISBN 978-0-444-53112-4. OCLC 162131565.
↑ W.-M. Yao et al. (Particle Data Group) (2006). "Review of Particle Physics: Quarks" (PDF). Journal of Physics G. 33 (1): 1. arXiv:astro-ph/0601168. Bibcode:2006JPhG...33....1Y. doi:10.1088/0954-3899/33/1/001. S2CID 117958297.
↑ Mark Thomson (5 September 2013). आधुनिक कण भौतिकी. Cambridge University Press. pp. 499–500. ISBN 978-1-107-29254-3.
↑ Martin, Jérôme (July 2012). "ब्रह्माण्ड संबंधी स्थिरांक समस्या के बारे में वह सब कुछ जो आप हमेशा से जानना चाहते थे (लेकिन पूछने से डरते थे)". Comptes Rendus Physique (in English). 13 (6–7): 566–665. arXiv:1205.3365. Bibcode:2012CRPhy..13..566M. doi:10.1016/j.crhy.2012.04.008. S2CID 119272967.
↑ The baryon number in SM is only conserved at the classical level. There are non-perturbative effects which do not conserve baryon number: Baryon Number Violation, report prepared for the Community Planning Study – Snowmass 2013
↑ The lepton number in SM is only conserved at the classical level. There are non-perturbative effects which do not conserve lepton number: see Fuentes-Martín, J.; Portolés, J.; Ruiz-Femenía, P. (January 2015). "Instanton-mediated baryon number violation in non-universal gauge extended models". Journal of High Energy Physics (in English). 2015 (1): 134. arXiv:1411.2471. Bibcode:2015JHEP...01..134F. doi:10.1007/JHEP01(2015)134. ISSN 1029-8479. or Baryon and lepton numbers in particle physics beyond the standard model
↑ The violation of lepton number and baryon number cancel each other out and in effect B − L is an exact symmetry of the Standard Model. Extension of the Standard Model with massive Majorana neutrinos breaks B-L symmetry, but extension with massive Dirac neutrinos does not: see Ma, Ernest; Srivastava, Rahul (2015-08-30). "Dirac or inverse seesaw neutrino masses from gauged B–L symmetry". Modern Physics Letters A (in English). 30 (26): 1530020. arXiv:1504.00111. Bibcode:2015MPLA...3030020M. doi:10.1142/S0217732315300207. ISSN 0217-7323. S2CID 119111538., Heeck, Julian (December 2014). "Unbroken B – L symmetry". Physics Letters B (in English). 739: 256–262. arXiv:1408.6845. Bibcode:2014PhLB..739..256H. doi:10.1016/j.physletb.2014.10.067., Vissani, Francesco (2021-03-03). "What is matter according to particle physics and why try to observe its creation in lab". Universe. 7 (3): 61. arXiv:2103.02642. Bibcode:2021Univ....7...61V. doi:10.3390/universe7030061.

[s1-10] 1.0 ^1.1 ^1.2 These are not ordinary abelian charges, which can be added together, but are labels of group representations of Lie groups.

[s2-11] 2.0 ^2.1 ^2.2 Mass is really a coupling between a left-handed fermion and a right-handed fermion. For example, the mass of an electron is really a coupling between a left-handed electron and a right-handed electron, which is the antiparticle of a left-handed positron. Also neutrinos show large mixings in their mass coupling, so it's not accurate to talk about neutrino masses in the flavor basis or to suggest a left-handed electron antineutrino.

[s4-12] 3.0 ^3.1 ^3.2 ^3.3 ^3.4 ^3.5 The Standard Model assumes that neutrinos are massless. However, many contemporary experiments prove that neutrinos oscillate between their flavour states, which could not happen if all were massless. It is straightforward to extend the model to fit these data but there are many possibilities, so the mass eigenstates are still open. See neutrino mass.

[s4b-13] 4.0 ^4.1 ^4.2 ^4.3 ^4.4 ^4.5 Yao, W.-M.; et al. (Particle Data Group) (2006). "Review of Particle Physics: Neutrino mass, mixing, and flavor change" (PDF). Journal of Physics G. 33 (1): 1. arXiv:astro-ph/0601168. Bibcode:2006JPhG...33....1Y. doi:10.1088/0954-3899/33/1/001. S2CID 117958297.

[s3-14] 5.0 ^5.1 ^5.2 ^5.3 The masses of baryons and hadrons and various cross-sections are the experimentally measured quantities. Since quarks can't be isolated because of QCD confinement, the quantity here is supposed to be the mass of the quark at the renormalization scale of the QCD scale.

[1] In fact, there are mathematical issues regarding quantum field theories still under debate (see e.g. Landau pole), but the predictions extracted from the Standard Model by current methods are all self-consistent. For a further discussion see e.g. R. Mann, chapter 25.

[NYT-20230911-2] Overbye, Dennis (11 September 2023). "Don't Expect a 'Theory of Everything' to Explain It All - Not even the most advanced physics can reveal everything we want to know about the history and future of the cosmos, or about ourselves". The New York Times. Archived from the original on 11 September 2023. Retrieved 11 September 2023.

[3] Lindon, Jack (2020). एलएचसी पर एटलस डिटेक्टर का उपयोग करते हुए एक ऊर्जावान जेट और बड़े लापता अनुप्रस्थ गति के साथ घटनाओं में डार्क एनर्जी, डार्क मैटर और मानक मॉडल हस्ताक्षरों से परे जेनेरिक के कण कोलाइडर जांच (PhD). CERN.

[fas.org-4] 4.0 ^4.1 Raby, Stuart; Slansky, Richard. "न्यूट्रिनो द्रव्यमान - उन्हें मानक मॉडल में कैसे जोड़ें" (PDF). FAS Project on Government Secrecy. Retrieved 3 November 2023.

[5] "न्यूट्रिनो दोलन आज". t2k-experiment.org.

[6] "संग्रहीत प्रति" (PDF). Archived from the original (PDF) on 2014-02-26. Retrieved 2014-02-26.

[7] "2.3.1 Isospin and SU(2), Redux". math.ucr.edu. Retrieved 2020-08-09.

[8] McCabe, Gordon. (2007). The structure and interpretation of the standard model. Amsterdam: Elsevier. pp. 160–161. ISBN 978-0-444-53112-4. OCLC 162131565.

[9] W.-M. Yao et al. (Particle Data Group) (2006). "Review of Particle Physics: Quarks" (PDF). Journal of Physics G. 33 (1): 1. arXiv:astro-ph/0601168. Bibcode:2006JPhG...33....1Y. doi:10.1088/0954-3899/33/1/001. S2CID 117958297.

[Thomson499-15] Mark Thomson (5 September 2013). आधुनिक कण भौतिकी. Cambridge University Press. pp. 499–500. ISBN 978-1-107-29254-3.

[16] Martin, Jérôme (July 2012). "ब्रह्माण्ड संबंधी स्थिरांक समस्या के बारे में वह सब कुछ जो आप हमेशा से जानना चाहते थे (लेकिन पूछने से डरते थे)". Comptes Rendus Physique (in English). 13 (6–7): 566–665. arXiv:1205.3365. Bibcode:2012CRPhy..13..566M. doi:10.1016/j.crhy.2012.04.008. S2CID 119272967.

[17] The baryon number in SM is only conserved at the classical level. There are non-perturbative effects which do not conserve baryon number: Baryon Number Violation, report prepared for the Community Planning Study – Snowmass 2013

[18] The lepton number in SM is only conserved at the classical level. There are non-perturbative effects which do not conserve lepton number: see Fuentes-Martín, J.; Portolés, J.; Ruiz-Femenía, P. (January 2015). "Instanton-mediated baryon number violation in non-universal gauge extended models". Journal of High Energy Physics (in English). 2015 (1): 134. arXiv:1411.2471. Bibcode:2015JHEP...01..134F. doi:10.1007/JHEP01(2015)134. ISSN 1029-8479. or Baryon and lepton numbers in particle physics beyond the standard model

[19] The violation of lepton number and baryon number cancel each other out and in effect B − L is an exact symmetry of the Standard Model. Extension of the Standard Model with massive Majorana neutrinos breaks B-L symmetry, but extension with massive Dirac neutrinos does not: see Ma, Ernest; Srivastava, Rahul (2015-08-30). "Dirac or inverse seesaw neutrino masses from gauged B–L symmetry". Modern Physics Letters A (in English). 30 (26): 1530020. arXiv:1504.00111. Bibcode:2015MPLA...3030020M. doi:10.1142/S0217732315300207. ISSN 0217-7323. S2CID 119111538., Heeck, Julian (December 2014). "Unbroken B – L symmetry". Physics Letters B (in English). 739: 256–262. arXiv:1408.6845. Bibcode:2014PhLB..739..256H. doi:10.1016/j.physletb.2014.10.067., Vissani, Francesco (2021-03-03). "What is matter according to particle physics and why try to observe its creation in lab". Universe. 7 (3): 61. arXiv:2103.02642. Bibcode:2021Univ....7...61V. doi:10.3390/universe7030061.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[lhf 1]

[lhf 2]

[lhf 3]

[lhf 4]

[lhf 5]

[10]

[11]

[12]

[13]

[14]

Anonymous

Search

मानक मॉडल का गणितीय सूत्रीकरण

क्वांटम क्षेत्र सिद्धांत

क्षेत्रों की वैकल्पिक प्रस्तुतियाँ

फर्मिअन्स

एक चिरल सिद्धांत

द्रव्यमान और अंतःक्रिया ईजेनस्थिति

धनात्मक और ऋणात्मक ऊर्जा

बोसोन

विघ्नकारी क्यूएफटी और अंतःक्रिया चित्र

मुक्त क्षेत्र

अंतःक्रिया के उद्देश्य और पथ अभिन्न दृष्टिकोण

लैग्रेंजियन औपचारिकता

गतिज पद

फर्मिअन क्षेत्र

गेज क्षेत्र

युग्मन उद्देश्य

इलेक्ट्रोवीक क्षेत्र

क्वांटम क्रोमोडायनामिक्स क्षेत्र

द्रव्यमान पद और हिग्स क्रियाविधि

द्रव्यमान पद

हिग्स क्रियाविधि

युकावा अंतःक्रिया

न्यूट्रिनो द्रव्यमान

विस्तृत जानकारी

क्षेत्र सामग्री विस्तार से

फर्मिअन सामग्री

मुक्त पैरामीटर

मानक मॉडल की अतिरिक्त समरूपताएँ

U(1) समरूपता

आवेशित और उदासीन धारा युग्म और फर्मी सिद्धांत

यह भी देखें

संदर्भ और बाहरी लिंक

Navigation

Wiki tools

Page tools

Other projects

Categories