सममिति विघात
भौतिकी में, समरूपता विघटन एक ऐसी घटना है जहां एक अव्यवस्थित किन्तु सममित स्थिति एक व्यवस्थित, किन्तु कम सममित स्थिति में कोलेप्स जाती है।[1] यह पतन अधिकांशत: अनेक संभावित द्विभाजन में से एक होता है जो एक कण ले सकता है क्योंकि यह कम ऊर्जा अवस्था में पहुंचता है। अनेक संभावनाओं के कारण, एक पर्यवेक्षक पतन के परिणाम को इच्छित मान सकता है। यह घटना क्वांटम क्षेत्र सिद्धांत (क्यूएफटी) और इसके अतिरिक्त , भौतिकी की समकालीन समझ के लिए मौलिक है।[2] विशेष रूप से, यह ग्लासो-वेनबर्ग-सलाम मॉडल में एक केंद्रीय भूमिका निभाता है जो इलेक्ट्रोवीक खंड मॉडलिंग करने वाले मानक मॉडल का भाग बनता है।
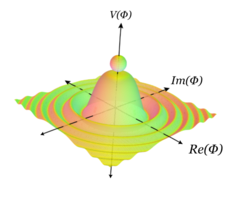
एक अनंत प्रणाली (मिन्कोवस्की स्थान) में समरूपता विघटित है, चूँकि परिमित प्रणाली (अथार्त , कोई भी वास्तविक सुपर-संघनित प्रणाली) में, प्रणाली कम पूर्वानुमानित होती है, किन्तु अनेक स्थितियों में क्वांटम टनलिंग होती है।[2][3] जो कि समरूपता को विघटित और सुरंग बनाना कण के गैर-सममित अवस्था में कोलेप्स से संबंधित है क्योंकि यह कम ऊर्जा की खोज करता है।[4]
समरूपता विघटन को दो प्रकारों में विभाजित किया जा सकता है, जो कि स्पष्ट समरूपता विघटन और सहज समरूपता विघटन है । उनकी विशेषता यह है कि क्या गति के समीकरण अपरिवर्तनीय होने में विफल रहते हैं, या निर्वात अवस्था अपरिवर्तनीय होने में विफल रहती है।
गैर-तकनीकी विवरण
यह खंड स्वतःस्फूर्त समरूपता विघटन का वर्णन करता है। समान्य आदमी के शब्दों में, यह विचार है कि भौतिक प्रणाली के लिए, सबसे कम ऊर्जा विन्यास (निर्वात अवस्था) प्रणाली का सबसे सममित विन्यास नहीं है। समान्य रूप से तीन प्रकार की समरूपताएं हैं जिन्हें तोड़ा जा सकता है: असतत, लाई समूह और गेज, बढ़ती तकनीकीता में क्रमबद्ध है।
असतत समरूपता वाले प्रणाली का एक उदाहरण लाल आरेख वाले चित्र द्वारा दिया गया है: गुरुत्वाकर्षण के अधीन, इस आरेख पर चलते हुए एक कण पर विचार करें। फलन द्वारा एक समान आरेख़ दिया जा सकता है। यह प्रणाली y-अक्ष में परावर्तन के अंतर्गत सममित है। कण के लिए तीन संभावित स्थिर अवस्थाएँ हैं: पहाड़ी की चोटी पर, या नीचे, पर जब कण शीर्ष पर होता है, तो विन्यास प्रतिबिंब समरूपता का सम्मान करता है: परावर्तित होने पर कण उसी स्थान पर रहता है। चूँकि , सबसे कम ऊर्जा विन्यास पर हैं। जब कण इनमें से किसी भी विन्यास में होता है, तो यह y-अक्ष में प्रतिबिंब के अनुसार स्थिर नहीं रहता है: प्रतिबिंब दो निर्वात स्थितियों को परिवर्तित कर देता है।
निरंतर समरूपता वाला एक उदाहरण पिछले उदाहरण के 3डी एनालॉग द्वारा दिया गया है, पहाड़ी के शीर्ष के माध्यम से एक अक्ष के चारों ओर आरेख को घुमाने से, या समकक्ष आरेख़ द्वारा दिया गया है। यह मूलतः मैक्सिकन टोपी की क्षमता का आरेख है। इसमें पहाड़ी के शीर्ष के माध्यम से अक्ष के चारों ओर घूमने से दी गई एक सतत समरूपता है (जो कि साथ ही किसी रेडियल विमान के माध्यम से प्रतिबिंब द्वारा एक असतत समरूपता भी है)। पुनः, यदि कण पहाड़ी के शीर्ष पर है तो यह घूर्णन के अनुसार स्थिर हो जाता है, किन्तु शीर्ष पर इसकी गुरुत्वाकर्षण ऊर्जा अधिक होती है। तल पर, यह अब घूर्णन के अनुसार अपरिवर्तनीय नहीं है किन्तु इसकी गुरुत्वाकर्षण संभावित ऊर्जा को कम कर देता है। इसके अतिरिक्त घूर्णन कण को एक ऊर्जा न्यूनतम विन्यास से दूसरे में ले जाता है। यहां एक नवीनता है जो पिछले उदाहरण में नहीं देखी गई थी: किसी भी निर्वात अवस्था से पहाड़ी के नीचे गर्त के चारों ओर घूमकर, केवल थोड़ी मात्रा में ऊर्जा के साथ किसी अन्य निर्वात अवस्था तक पहुंचना संभव है, जबकि पिछले उदाहरण में, अन्य निर्वात तक पहुँचने के लिए, कण को पहाड़ी को पार करना होगा, जिसके लिए बड़ी मात्रा में ऊर्जा की आवश्यकता होगी।
गेज समरूपता विघटित सबसे सूक्ष्म है, किन्तु इसके महत्वपूर्ण भौतिक परिणाम होते हैं। समान्य रूप से कहें तो, इस खंड के प्रयोजनों के लिए गेज समरूपता अंतरिक्ष समय में प्रत्येक बिंदु पर निरंतर समरूपता वाले प्रणाली का असाइनमेंट है। गेज समरूपता गेज क्षेत्र के लिए बड़े मापदंड पर उत्पादन को रोकती है, फिर भी बड़े मापदंड पर गेज क्षेत्र (डब्ल्यू और जेड बोसॉन) देखे गए हैं। इस असंगति को हल करने के लिए सहज समरूपता विघटित विकसित किया गया था। विचार यह है कि ब्रह्मांड के प्रारंभिक चरण में यह उच्च ऊर्जा अवस्था में था, जो पहाड़ी के शीर्ष पर कण के अनुरूप था, और इसलिए इसमें पूर्ण गेज समरूपता थी और सभी गेज क्षेत्र द्रव्यमान रहित थे। जैसे ही यह ठंडा हुआ, यह निर्वात के विकल्प में बस गया, इस प्रकार स्वचालित रूप से समरूपता टूट गई, इस प्रकार गेज समरूपता को हटा दिया गया और उन गेज क्षेत्रों की बड़े मापदंड पर पीढ़ी की अनुमति दी गई। पूर्ण स्पष्टीकरण अत्यधिक तकनीकी है: विद्युत अशक्त अंतःक्रिया देखें।
सहज समरूपता विघटन
स्वतःस्फूर्त समरूपता विखंडन (एसएसबी) में, प्रणाली की गति के समीकरण अपरिवर्तनीय होते हैं, किन्तु कोई भी निर्वात अवस्था (निम्नतम ऊर्जा अवस्था) नहीं होती है।
दो-तरफा समरूपता वाले उदाहरण के लिए, यदि कोई परमाणु है जिसमें दो निर्वात अवस्थाएँ हैं, तो इनमें से किसी एक अवस्था पर अधिकृत करने से दो-गुना समरूपता विघटित हो जाती है। जैसे ही प्रणाली कम ऊर्जा तक पहुंचता है, स्थिति में से किसी एक को चुनने का यह कार्य एसएसबी है। जब ऐसा होता है, तो परमाणु अब सममित (परावर्तक रूप से सममित) नहीं रह जाता है और निम्न ऊर्जा अवस्था में कोलेप्स जाता है।
इस तरह की समरूपता को विघटित ऑर्डर पैरामीटर द्वारा पैरामीट्रिज्ड होता है। इस प्रकार की समरूपता विघटन का विशेष स्थिति गतिशील समरूपता विघटन है।
क्वांटम क्षेत्र सिद्धांत (क्यूएफटी) की लैग्रैन्जियन सेटिंग में, लैग्रैन्जियन क्वांटम क्षेत्रों का एक कार्यात्मक है जो समरूपता समूह की कार्रवाई के अनुसार अपरिवर्तनीय है। चूँकि जब कण कम ऊर्जा में कोलेप्स जाता है तो निर्वात अपेक्षा मूल्य नहीं बन सकता है के अनुसार अपरिवर्तनीय रहें। इस उदाहरण में, यह आंशिक रूप से की समरूपता को एक उपसमूह में तोड़ देगा। यह सहज समरूपता विघटन है।
चूँकि, गेज समरूपता के संदर्भ में, एसएसबी वह घटना है जिसके द्वारा गेज-अपरिवर्तनीयता के अतिरिक्त गेज सिद्धांत 'द्रव्यमान प्राप्त करता है' कि ऐसे क्षेत्र द्रव्यमान रहित हों। ऐसा इसलिए है क्योंकि गेज समरूपता का एसएसबी गेज-इनवेरिएंस को तोड़ देता है, और ऐसा ब्रेक बड़े मापदंड पर गेज क्षेत्रों के अस्तित्व की अनुमति देता है। यह गोल्डस्टोन के प्रमेय से महत्वपूर्ण छूट है| गोल्डस्टोन के प्रमेय, जहां गोल्डस्टोन बोसोन या नंबू-गोल्डस्टोन बोसोन द्रव्यमान प्राप्त कर सकता है, इस प्रक्रिया में हिग्स बॉसन बन सकता है।[5]
इसके अतिरिक्त , इस संदर्भ में मानक रहते हुए 'समरूपता तोड़ने' का उपयोग मिथ्या नाम है, क्योंकि गेज 'समरूपता' वास्तव में समरूपता नहीं है किन्तु प्रणाली के विवरण में अतिरेक है। गणितीय रूप से, यह अतिरेक तुच्छीकरण (गणित) का विकल्प है, जो कुछ सीमा तक आधार के विकल्प से उत्पन्न होने वाले अतिरेक के समान है।
स्वतःस्फूर्त समरूपता का विघटन चरण संक्रमणों से भी जुड़ा हुआ है। उदाहरण के लिए, आइसिंग मॉडल में, जैसे ही प्रणाली का तापमान महत्वपूर्ण तापमान से नीचे गिरता है, निर्वात की समरूपता विघटित हो जाती है, जिससे प्रणाली का एक चरण संक्रमण होता है।
स्पष्ट समरूपता विघटन
स्पष्ट समरूपता विघटित करने (ईएसबी) में, प्रणाली का वर्णन करने वाले गति के समीकरण विघटित हुई समरूपता के अनुसार भिन्न होते हैं। हैमिल्टनियन यांत्रिकी या लैग्रेंजियन यांत्रिकी में, ऐसा तब होता है जब हैमिल्टनियन (या लैग्रैन्जियन) में कम से कम शब्द होता है जो स्पष्ट रूप से दी गई समरूपता को विघटित करता है।
हैमिल्टनियन सेटिंग में, इसका अधिकांशत: अध्ययन किया जाता है जब हैमिल्टनियन को लिखा जा सकता है।
यहां एक 'बेस हैमिल्टनियन' है, जिसमें कुछ स्पष्ट समरूपता है। अधिक स्पष्ट रूप से, यह (लाई) समूह की कार्रवाई के अनुसार सममित है। अधिकांशत: यह एक पूर्णांक हैमिल्टनियन है।
जहाँ एक अस्पष्ट या अंतःक्रिया हैमिल्टनियन है। यह की कार्रवाई के अनुसार अपरिवर्तनीय नहीं है। यह अधिकांशत: एक छोटे, परेशान करने वाले पैरामीटर के समानुपाती होता है।
यह मूलतः क्वांटम यांत्रिकी में अस्पष्ट सिद्धांत का प्रतिमान है। इसके उपयोग का उदाहरण परमाणु स्पेक्ट्रा की निकटतम संरचना का पता लगाना है।
उदाहरण
समरूपता विघटित करने से निम्नलिखित में से कोई भी परिदृश्य आवरण हो सकता है:
- किसी संरचना के स्पष्ट रूप से यादृच्छिक गठन द्वारा भौतिकी के अंतर्निहित नियमों की सटीक समरूपता को विघटित करता है ;
- भौतिकी में स्थिति जिसमें जमीनी स्थिति में प्रणाली की तुलना में कम समरूपता होती है;
- ऐसी स्थितियाँ जहां प्रणाली की वास्तविक स्थिति गतिशीलता की अंतर्निहित समरूपता को प्रतिबिंबित नहीं करती है क्योंकि स्पष्ट रूप से सममित स्थिति अस्थिर है (स्थिरता स्थानीय गुण विषमता की मूल्य पर प्राप्त की जाती है);
- ऐसी स्थितियां जहां किसी सिद्धांत के समीकरणों में कुछ समरूपताएं हो सकती हैं, चूँकि उनके समाधान नहीं हो सकते (समरूपताएं छिपी हुई हैं)।
भौतिकी साहित्य में विचार की गई विघटित हुई समरूपता के पहले स्थितियों में से गुरुत्वाकर्षण और हाइड्रोस्टैटिक संतुलन में असम्पीडित प्रवाह के समान रूप से घूमने वाले निकाय द्वारा लिए गए रूप से संबंधित है। कार्ल गुस्ताव जैकब जैकोबी[6] और शीघ्र ही इसके पश्चात् में लिओविले,[7] 1834 में, इस तथ्य पर विचार की गई कि त्रि-अक्षीय दीर्घवृत्त इस समस्या के लिए संतुलन समाधान था जब घूर्णन निकाय की गुरुत्वाकर्षण ऊर्जा की तुलना में गतिज ऊर्जा निश्चित महत्वपूर्ण मूल्य से अधिक हो गई। मैकलॉरिन गोलाकार द्वारा प्रस्तुत अक्षीय समरूपता इस द्विभाजन बिंदु पर विघटित हो गई है। इसके अतिरिक्त , इस द्विभाजन बिंदु के ऊपर, और निरंतर कोणीय गति के लिए, गतिज ऊर्जा को कम करने वाले समाधान मैकलॉरिन गोलाकार के अतिरिक्त गैर-अक्षीय सममित जैकोबी दीर्घवृत्त हैं।
यह भी देखें
- हिग्स तंत्र
- क्यूसीडी वैक्यूम
- 1964 पीआरएल समरूपता पेपर विघटन
संदर्भ
- ↑ Heylighen, Francis (2023). "Entanglement, Symmetry Breaking and Collapse: Correspondences Between Quantum and Self-Organizing Dynamics". Foundations of Science. Brussels, Belgium. 28: 85–107. doi:10.1007/s10699-021-09780-7. S2CID 4568832 – via SpringerLink.
- ↑ 2.0 2.1 Gross, David J. (1996-12-10). "मौलिक भौतिकी में समरूपता की भूमिका". PNAS. 93 (25): 14256–14259. doi:10.1073/pnas.93.25.14256. PMC 34470. PMID 11607718.
- ↑ Ohira, Ryutaro; Mukaiyama, Takashi; Toyoda, Kenji (2020-02-01). "ट्रैप्ड-आयन क्वांटम टनलिंग रोटर में घूर्णी समरूपता को तोड़ना". Physical Review A. American Physical Society. 101 (2): 022106. arXiv:1907.07404. Bibcode:2020PhRvA.101b2106O. doi:10.1103/PhysRevA.101.022106.
- ↑ Castellani, Elena; Teh, Nicholas; Brading, Katherine (2017-12-14). Edward, Zalta (ed.). "समरूपता और समरूपता का टूटना". Stanford Encyclopedia of Philosophy (Fall 2021 ed.). Metaphysics Research Lab, Stanford University.
- ↑ Law, Johnathan; Rennie, Richard (2009). "Goldstone's theorem". भौतिकी का एक शब्दकोश (6 ed.). Oxford University Press. doi:10.1093/acref/9780199233991.001.0001. ISBN 9780199233991. Retrieved 2023-03-01.
- ↑ Jacobi, C.G.J. (1834). "Über die figur des gleichgewichts". Annalen der Physik und Chemie. 109 (33): 229–238. Bibcode:1834AnP...109..229J. doi:10.1002/andp.18341090808.
- ↑ Liouville, J. (1834). "Sur la figure d'une masse fluide homogène, en équilibre et douée d'un mouvement de rotation". Journal de l'École Polytechnique (14): 289–296.
बाहरी संबंध
 Quotations related to Symmetry breaking at Wikiquote
Quotations related to Symmetry breaking at Wikiquote
