घातीय प्रकार

For प्ररूप सिद्धांत और प्रोग्रामिंग भाषाओं में घातीय प्रकार, see फलन प्ररूप.

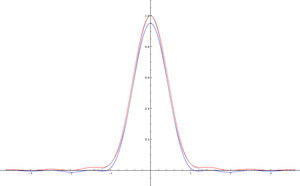
$e^{-\pi z^{2}}$ फलन का ग्राफ ग्रे रंग में है, गाऊसी वास्तविक अक्ष तक ही सीमित है। फिर गॉसियन में घातीय प्ररूप नहीं होता है, किन्तु लाल और नीले रंग में कार्य एक तरफा सन्निकटन होते हैं जिनमें घातांक प्रकार $2\pi$ होता है.

सम्मिश्र विश्लेषण में, गणित की एक शाखा, एक होलोमोर्फिक फलन को घातीय प्ररूप C का कहा जाता है यदि इसकी वृद्धि घातीय फलन $e^{C|z|}$ द्वारा सीमित होती है किसी वास्तविक संख्या के लिए वास्तविक-मान स्थिरांक $C$ जैसा $|z|\to \infty$. जब कोई फलन इस तरह से घिरा होता है, तो इसे अन्य सम्मिश्र फलन की श्रृंखला पर कुछ प्रकार के अभिसरण योगों के रूप में व्यक्त करना संभव होता है, साथ ही यह समझना भी संभव होता है कि बोरेल योग जैसी तकनीकों को क्रियान्वित करना कब संभव है, या, उदाहरण के लिए , मेलिन परिवर्तन को क्रियान्वित करने के लिए, या यूलर-मैकलॉरिन फॉर्मूला का उपयोग करके सन्निकटन करने के लिए। सामान्य स्थितियों को नचबिन के प्रमेय द्वारा नियंत्रित किया जाता है,जो $e^{z}$ के विपरीत एक सामान्य फलन $\Psi (z)$ के लिए $\Psi$-प्रकार की अनुरूप धारणा को परिभाषित करता है।.

मूल विचार

सम्मिश्र तल पर परिभाषित एक फलन $f(z)$ को घातीय प्रकार का कहा जाता है यदि वास्तविक-मान वाले स्थिरांक $M$ और $\tau$ उपस्तिथ हों जैसे कि

$\left|f\left(re^{i\theta }\right)\right|\leq Me^{\tau r}$

$r\to \infty$ की सीमा में. यहाँ, सम्मिश्र चर $z$ को $z=re^{i\theta }$ रूप में लिखा गया था जिससे कि इस बात पर ज़ोर देना कि सीमा सभी दिशाओं में $\theta$ को बनाए रखना चाहिए। ऐसे सभी $\tau$ के न्यूनतम के लिए $\tau$ स्थित रहें $\tau$, तो कोई कहता है कि फलन $f$ घातीय प्ररूप $\tau$ का है .

उदाहरण के लिए, चलो $f(z)=\sin(\pi z)$. फिर कोई कहता है $\sin(\pi z)$ घातीय प्ररूप $\pi$ का है, क्योंकि $\pi$ वह सबसे छोटी संख्या है जो काल्पनिक अक्ष के साथ $\sin(\pi z)$ को सीमित करती है. इसलिए, इस उदाहरण के लिए, कार्लसन का प्रमेय क्रियान्वित नहीं हो सकता, क्योंकि इसके लिए इससे कम घातीय प्ररूप $\pi$ के फलनों की आवश्यकता होती है. इसी तरह, यूलर-मैकलॉरिन फॉर्मूला भी क्रियान्वित नहीं किया जा सकता है, क्योंकि यह भी एक प्रमेय को व्यक्त करता है जो अंततः परिमित अंतर के सिद्धांत में निहित है।

औपचारिक परिभाषा

होलोमोर्फिक फलन $F(z)$ घातीय प्ररूप $\sigma >0$ का कहा जाता है यदि प्रत्येक $\varepsilon >0$ के लिए वहाँ एक वास्तविक-मान स्थिरांक $A_{\varepsilon }$ उपस्तिथ है ऐसा है कि

$|F(z)|\leq A_{\varepsilon }e^{(\sigma +\varepsilon )|z|}$

$|z|\to \infty$ के लिए जहाँ $z\in \mathbb {C}$. हम कहते हैं $F(z)$ यदि घातीय प्ररूप का है यदि $F(z)$ कुछ $\sigma >0$ घातीय प्ररूप $\sigma$ का है. जो संख्या

$\tau (F)=\sigma =\displaystyle \limsup _{|z|\rightarrow \infty }|z|^{-1}\log |F(z)|$

$F(z)$ का घातीय प्ररूप है. यहां श्रेष्ठ सीमा का कारण किसी दिए गए त्रिज्या के बाहर अनुपात के सर्वोच्च की सीमा है क्योंकि त्रिज्या अनंत तक जाती है। यह किसी दिए गए त्रिज्या पर अनुपात के अधिकतम से श्रेष्ठ सीमा भी है क्योंकि त्रिज्या अनंत तक जाती है। उच्चतम सीमा त्रिज्या पर अधिकतम होने पर भी उपस्तिथ हो सकती है $r$ जैसी कोई सीमा नहीं है $r$ अनंत तक जाता है. उदाहरण के लिए, फलन के लिए

$F(z)=\sum _{n=1}^{\infty }{\frac {z^{10^{n!}}}{(10^{n!})!}}$

का मान है

$(\max _{|z|=r}\log |F(z)|)/r$

पर $r=10^{n!-1}$ का प्रभुत्व है $n-1^{\text{st}}$ शब्द इसलिए हमारे पास स्पर्शोन्मुख अभिव्यक्तियाँ हैं:

${\begin{aligned}\left(\max _{|z|=10^{n!-1}}\log |F(z)|\right)/10^{n!-1}&\sim \left(\log {\frac {(10^{n!-1})^{10^{(n-1)!}}}{(10^{(n-1)!})!}}\right)/10^{n!-1}\\&\sim (\log 10)\left[(n!-1)10^{(n-1)!}-10^{(n-1)!}(n-1)!\right]/10^{n!-1}\\&\sim (\log 10)(n!-1-(n-1)!)/10^{n!-1-(n-1)!}\\\end{aligned}}$

और यह शून्य हो जाता है $n$ अनंत तक जाता है, किन्तु $F(z)$ फिर भी यह घातीय प्ररूप 1 का है, जैसा कि बिंदुओं $z=10^{n!}$ को देखकर देखा जा सकता है.

सममित उत्तल पिंड के संबंध में घातीय प्ररूप

Stein (1957) ने कई सम्मिश्र चर के संपूर्ण फलन के लिए घातीय प्ररूप का सामान्यीकरण दिया है। मान लीजिए $K$ एक उत्तल समुच्चय, सघन तत्व और सममित उपसमुच्चय $\mathbb {R} ^{n}$ है. यह ज्ञात है कि हर ऐसे के लिए $K$ एक संबद्ध मानदंड $\|\cdot \|_{K}$ है (गणित) उस गुण के साथ

$K=\{x\in \mathbb {R} ^{n}:\|x\|_{K}\leq 1\}.$

दूसरे शब्दों में, $K$ में यूनिट बॉल $\mathbb {R} ^{n}$ है इसके संबंध में समुच्चय $\|\cdot \|_{K}$.

$K^{*}=\{y\in \mathbb {R} ^{n}:x\cdot y\leq 1{\text{ for all }}x\in {K}\}$

$\mathbb {R} ^{n}$ को ध्रुवीय समुच्चय कहा जाता है और यह उत्तल समुच्चय, सघन तत्व और सममित उपसमुच्चय भी है. इसके अतिरिक्त, हम लिख सकते हैं

$\|x\|_{K}=\displaystyle \sup _{y\in K^{*}}|x\cdot y|.$

हम विस्तार करते हैं $\|\cdot \|_{K}$ से $\mathbb {R} ^{n}$ को $\mathbb {C} ^{n}$ द्वारा

$\|z\|_{K}=\displaystyle \sup _{y\in K^{*}}|z\cdot y|.$

एक संपूर्ण फलन $F(z)$ का $n$-सम्मिश्र चर को घातीय प्ररूप $K$ का कहा जाता है यदि प्रत्येक के लिए $\varepsilon >0$ वहाँ एक वास्तविक-मान स्थिरांक उपस्तिथ $A_{\varepsilon }$ है ऐसा है कि

$|F(z)|<A_{\varepsilon }e^{2\pi (1+\varepsilon )\|z\|_{K}}$

सभी के लिए $z\in \mathbb {C} ^{n}$.

फ्रेचेट समष्टि

घातीय प्ररूप के फलनों का संग्रह $\tau$ मानदंड (गणित) के गणनीय वर्ग द्वारा प्रेरित टोपोलॉजिकल समष्टि द्वारा एक पूर्ण समष्टि, समान समष्टि, अर्थात् फ़्रेचेट समष्टि, बना सकता है

$\|f\|_{n}=\sup _{z\in \mathbb {C} }\exp \left[-\left(\tau +{\frac {1}{n}}\right)|z|\right]|f(z)|.$

यह भी देखें

• पेली-वीनर प्रमेय
• पेली-वीनर समष्टि

संदर्भ

• Stein, E.M. (1957), "Functions of exponential type", Ann. of Math., 2, 65: 582–592, doi:10.2307/1970066, JSTOR 1970066, MR 0085342